让智慧在行动中闪光

魏常安

【案例】在进行《圆》的概念课时，教师设计了如下的两个情境。

情境1：教师提供了两种道具：棉线和橡皮筋，请同学们利用棉线和橡皮筋分别画圆，并交流做法和体会。

教师：根据大家的操作，有何发现？

学生：棉线可以画圆，橡皮筋不行。

教师：能否解释一下两种工具为什么会产生完全不一样的结果呢？

学生（经过讨论）：棉线有固定的长短，而皮筋在操作中，长短一直在变。

教师：这种结果影响了什么因素，使之无法形成圆。

学生：半径。

教师：说得很对，让我一起利用棉线合作在黑板上画出圆形，能描述一下刚才画图的步骤吗？

学生纷纷举手。

……

情境2：滚弹珠的游戏（图1）。若全班学生都沿着红线站成一横排，请问游戏对所有学生公平吗？

学生：不公平，有人距离洞口近，有有人距离洞口远。

教师：那全部学生应该怎样站，就可以公平了？

学生：只要根据洞口的位置，站成圆形就好。

引出：圆上的各点到圆心的距离都等于半径。

问题1：甲、乙两人分别站在⊙O（图2）上的A、B两点处，他俩正准备参加游戏，后来丙、丁也来参加，并分别站在了图中的P、Q两点处。如果你是甲同学，你会有怎样的看法？

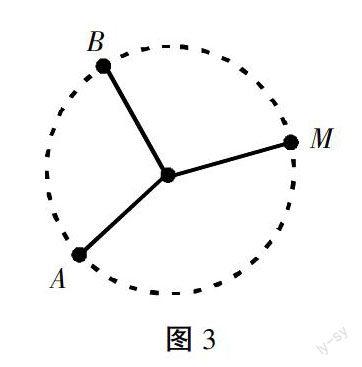
问题2：再后来，小明同学也来参加游戏，他站的位置是图中的M点（图3），但他发现地上的线几乎看不清了。请问小明同学怎样知道自己恰好站在圆上？

【案例剖析】情境1中学生对圆的初步印象在小学已经形成，而要由直观图形抽象得出圆的描述性定义，对学生来说是一个难点，也是培养学生几何意识的重要一步。如果教师直接让学生来描述圆的概念，我想学生是很难准确描述的。而案例中教师通过精心的设计，让学生通过操作，分别利用棉线和橡皮筋画圆，从两种不同的结果中产生认知冲突，进一步分析原因，两种工具的区别在于棉线有固定的长度，而橡皮筋在操作中长度不停地在变。由此产生分析圆的必要条件：圆心和半径。在师生的进一步共同操作中，学生感知形成圆的过程，通过归纳关键步骤，逐步在头脑中形成这样几个关键词：一端要固定，绷直，另一端旋转一周，形成圆的描述性定义：线段OP绕着它固定的一个端点O在平面内旋转一周，另一端点P运动所形成的图形叫圆。圆的概念不是教师的讲解所得，而是通过学生自己的操作过程中感悟所得，而且在圆的定义的建构过程中让学生经历了观察、实验、猜想、推理、交流、反思的过程，感悟知识的形成和应用。对于学生理解数学知识与方法、形成良好的数学思维习惯和应用意识有着重要的作用。情境2中通过学生耳熟能详的滚弹珠活动，将“点与圆的位置关系”本质内容蕴含其中，在游戏条件逐步变化的过程中将学生的理解引向深入。围绕“滚弹珠”这一贴近学生生活化的主线，学生不仅节约了熟悉背景的时间，而且形成了较为系统的知识，通过判断参与游戏的公平性，自然而然得到了圆的相关知识，进一步在观察和判断点和圆的位置关系中，得到d与r之间的数量关系，体现了数形结合的思想，更重要的是学会“数眼看生活”，形成了一定的运用意识。在设计过程中，教师力求将情境和知识完美结合起来，实现学生“身临其境”的目的，不仅将学生的积极性充分地调动起来，更是将写生的创新精神激发出来，与其说学生的一些创新想法是由教师启发出来，不如说是被教师设置的情境逼出的。这正说明我们在教学实践中要放手，学生只有亲身参与教师精心设计的教学活动，才能在数学思考、问题解决和情感态度方面得到发展。