Convective mass transfer enhancement in a membrane channel by delta winglets and their comparison with rectangular winglets☆
Jingchun Min *,Bingqiang Zhang
1 School of Aerospace,Tsinghua University,Beijing 100084,China
2 Institute of Spacecraft Engineering,China Academy of Space Technology,Beijing 100094,China
3 Beijing Key Laboratory of Space Thermal Control Technology,Beijing 100094,China
Keywords:Membrane process Concentration polarization Mass transfer enhancement Delta winglet Pumping power
ABSTRACT Numerical calculations were conducted to simulate the flow and mass transfer in narrow membrane channels equipped with delta winglets,which are often used as longitudinal vortex generators to enhance heat transfer in heat exchanger applications.The channel consists of an impermeable solid wall and a membrane.The delta winglets are attached to the solid wall surface to enhance the mass transfer near the membrane surface and suppress the concentration polarization.The winglet performance was evaluated in terms of concentration polarization factor versus consumed pumping power.Calculations were implemented for NaCl solution flow in a membrane channel having a height of 2.0 mm for Reynolds numbers ranging from 400 to 1000.The delta winglets were optimized under equal pumping power condition,and the results of optimization suggest winglet heightof5/6 of the channel height,as pectratio of2.0,attack angle of30°,and a winglet interval equal to the channel height.The optimal delta winglets were compared with the optimal rectangular winglets we found previously,and it is shown that the rectangular winglets yield a somewhat better performance than the delta winglets.
1.Introduction
Ultra filtration and nanofiltration are typical pressure-driven membrane separation processes[1,2].In such processes,there existso-called concentration polarization phenomena that deteriorate permeate quality and reduce permeate flux,so the suppression of concentration polarization is of practical importance.
The present research continues our previous work[3],in which we numerically simulated the flow and mass transfer in narrow membrane channels equipped with various flow disturbers aiming at enhancing the convective mass transfer near the membrane surface by suppressing the concentration polarization.We compared the rectangular winglets with the traditional flow disturbers including circular cylinder[4-11],four-prism[9-11]and tri-prism[9,10],which were employed to mimic the traditional spacer filaments in a membrane module,and found that the former was more effective than the latter three in reducing the concentration polarization under equal pumping power condition.
There are many studies that support the effectiveness and superiority of the winglet-type longitudinal vortex generators(WLVGs)in enhancing heat transfer in heat exchanger applications[12-19].The most attractive character of such vortex generators is that they can increase the heat transfer coefficient with a relatively low pressure drop penalty.There are two typical types of WLVG:one is the delta winglet and the other is the rectangular winglet.Extensive studies have been done to investigate the heat transfer enhancing effects of WLVGs,most of them are on delta winglets[12-15]and others on rectangular winglets[16]or both[17-19].
Although the effects of WLVG in augmenting heat transfer have been fully confirmed,little information is available on their effects in augmenting mass transfer in a membrane channel,except for our previous work[3].It should be noted that such effects are not self-evident,because there are some key differences between the use of WLVGs for heat transfer enhancement and that for mass transfer enhancement.For instance,when WLVGs are used in a finned tube heat exchanger,they are setup on the fin surface to enhance the convective heat transfer near the fin surface on which they are mounted;when WLVGs are employed in a membrane module,however,they are set up on the solid wall to augment the convective mass transfer near the membrane surface opposite to the wall.Besides,since the Schmidt number is much larger than Prandtl number,the convective mass transfer boundary layer is substantially thinner than the convective heat transfer boundary layer,implying that the mass transfer enhancement is more difficult than the heat transfer enhancement.
In our previous work[3],we tried to introduce the WLVG technique into the enhanced mass transfer area and chose to use the rectangular winglets to enhance the convective mass transfer in a membrane channel.We evaluated their mass transfer enhancing effects in terms of concentration polarization factor versus consumed pumping power and found that they had better performance than the traditional flow disturbers.In the present research,we devote to investigate the effects of the delta winglets,which are one of the abovementioned two typical types of WLVGs,in augmenting the convective mass transfer to reduce the concentration polarization in a membrane channel having a height of 2.0 mm for Reynolds numbers ranging from 400 to 1000.Delta winglets are first optimized in geometry and arrangement under the equal pumping power condition,and then compared with the rectangular winglets optimized in our previous research[3].
2.Calculation Method
2.1.Physical model
Fig.1 shows the basic membrane channel used in this study,which consists of an impermeable solid wall and a membrane.The channel height is H and the channel length is L=35H.Delta winglets are installed on the solid wall and locate 5H downstream from the channel inlet.Fig.2 depicts the geometry and arrangement of the delta winglets,all of which are set up with an angle attacking to the entering solution flow.Winglets are arranged in pairs to form alternate V and Λ configuration,with the former being called a convex winglet pair and the latter a concave winglet pair.Because of symmetry in geometry,the computational domain is chosen to include one channel height,the entire channel length,and a channel width that just involves a single winglet,as illustrated by Fig.1,which also shows the coordinate system adopted in this study.The domain has a height of H,a length of L,and a width of W,which is equal to the winglet interval.The representative geometry and arrangement of the delta winglets are set as follows(Fig.2):the winglet height h=H/2,the winglet aspect ratio σ=l/h=2.0,the winglet attack angle β =30°and the winglet interval W=1.5H,as summarized in Table 1.Note that the winglet thickness is zero.

Fig.1.Membrane channel with delta winglets.

Table 1 Representative delta winglet parameters
2.2.Numerical simulation
Solution flow in membrane channel is assumed to be steady and incompressible with constant properties.RNG k-ε model is used to simulate the flow in channels.As boundary conditions,symmetry boundaries are employed on both sides of the computational domain shown in Fig.1,with no slip conditions being applied to both the solid wall and the membrane surface.The fluid inlet velocity is assumed to have a parabolic profile over the channel height to reduce the inlet velocity influence on mass transfer.Fluid flowing out of the channel is assumed to exist in a fully developed condition where all changes for the flow parameters are equal to zero.The solute concentration distribution at the membrane surface is determined by the mass balance among the convection,reverse diffusion,and permeate fluxes.Equations governing the solution flow and solute transport as well as those formulating the boundary conditions are described in details in our previous paper[3].
The governing equations are solved under the boundary conditions using Fluent V6.3 based on the finite volume method.The mass balance at the solution/membrane interface is realized through the user defined function(UDF)in Fluent.For each simulation,the numerical grids are refined until a grid independent solution is obtained.
2.3.Data reduction
The concentration polarization factor is defined by[9,10,21,22]

The local concentration polarization factor at position of x is calculated from

where wbis the solute mass fraction of the bulk solution and wwis the solute mass fraction at the feed solution/membrane interface.The concentration polarization factor averaged over a membrane surface area from x1to x2is given by
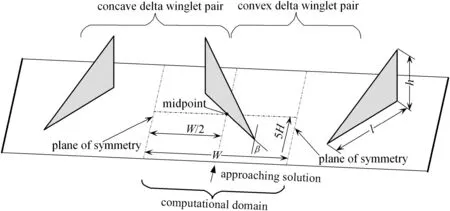
Fig.2.Geometry and arrangement of delta winglets.

Considering the feature of the concentration polarization evolution along the channel length,the starting and ending points of the above integral are taken to be x1=3H and x2=13H in this research.The total pressure at a channel cross-section is represented by

Note that the total pressure is the sum of the static pressure and dynamic pressure(velocity pressure)[23].The pumping power consumed for solution flow is computed from

where V is the volumetric flow rate of the feed solution corresponding to a channel width of W,and P1and P2are the pressures at the channel cross sections of x1=3H and x2=13H.
2.4.Model validation
To validate our model,calculations were carried out to simulate the concentration polarization in a membrane channel in nanofiltration investigated by de Pinho et al.[20],who performed both experimental and numerical studies of NaCl solution flow and mass transfer in an empty membrane channel having a height of 0.7 mm.A good agreement was obtained between our calculation results and the de Pinho data,supporting the reliability of our numerical procedure.A detailed description of the comparisons can be found in our previous paper[3].
3.Results and Discussion
Consider NaCl solution flow in membrane channels having a height of H=2.0 mm and a length of L=35H=70 mm.Calculations were conducted on channels with and without delta winglets for feed solute mass fraction w0=2.0×10-4kg·kg-1,permeate flux J=1.36×10-5m·s-1,and permeate composition wp=3.7×10-5kg·kg-1,with Reynolds numbers ranging from 400 to 1000,which correspond to entering solution velocities from 0.1786 to 0.4464 m·s-1.The values of w0,J,and wptogether define the membrane permeability.Table 2 presents the physical and transport properties of NaCl solution at 25°C.Note that these values are all the same as those used in our previous research[3].

Table 2 NaCl solution physical and transport properties
Calculations were first carried out on the Table 1 winglets.Fig.3 illustrates the solute mass fraction distributions at the membrane surfaces in channels with and without delta winglets for Re=600.The channel with delta winglets shows a more complicated mass fraction distribution because of the flow disturbing effect of the winglets.Different mass fraction distributions exist in the regions containing the convex and concave winglet pairs(defined in Fig.2).A large mass fraction is observed in the region containing the convex winglet pair while a small mass fraction is seen in that containing the concave winglet pair,with a large mass fraction meaning a severe concentration polarization.
Fig.4 is a vector plot of vortex velocity at a cross-section of x/H=6 for channel with delta winglets for Re=600.The figure shows that each winglet produces one vortex,with the concave winglet pair(left pair)generating two counter-rotating vortices and an upward flow to wash the membrane surface,while the convex winglet pair(right pair)generating two counter-rotating vortices and a downward flow to wash the solid wall surface.The upward flow thins the concentration boundary layer near the membrane surface,causing an enhanced mass transfer and consequently a small mass fraction at the membrane surface as observed in Fig.3,whereas the downward flow thickens the concentration boundary layer near the membrane surface,causing a reduced mass transfer and consequently a large mass fraction at the membrane surface as seen in the same figure.We note that there may exist two mechanisms for the thinned concentration boundary layer near the membrane surface:one is that the secondary flow towards the membrane surface,and the other is that such a flow increases the gradient of x-velocity component at the membrane surface,which acts to thin the concentration boundary layer.
3.1.Parametric optimization of delta winglets
Calculations were further implemented to investigate the winglet parametric effects on the winglet performance for the purpose of winglet optimization.There are fourkey parameters to define the winglet geometry and arrangement,including the winglet height h,aspect ratio σ =l/h,attack angle β,and winglet interval W.Calculations were done with the Table 1 data as a basis.In each calculation,only one parameter was varied with the other parameters remaining unchanged.The simulations used w0=0.2×10-3kg·kg-1,J=1.36×10-5m·s-1,and wp=3.7×10-5kg·kg-1.
Fig.5 illustrates the effects of the winglet height(h)on the concentration polarization and pressure drop characteristics for Re=600,with Fig.5(a)for concentration polarization factor(Гx)and Fig.5(b)for pressure(P).The abscissa is the dimensionless longitudinal distance from the channel inlet(x/H).The data for the empty channel are also included to serve as a baseline.As the winglet height increases,the concentration polarization factor decreases while the pressure drop increases.
Fig.6 shows the area-averaged concentration polarization factor(ГA)plotted against the consumed pumping power(E)for various winglet heights.For each height,there are four data points,which correspond to the cases of Re=400,600,800,and 1000,respectively.For a fixed pumping power,the winglets having a height of h=5H/6 yield the lowest concentration polarization factor,or for a fixed concentration polarization factor,such winglets give the smallest pumping power,so h=5H/6 is the best winglet height.
Fig.7 illustrates the effects of winglet aspect ratio(σ)on concentration polarization and pressure drop characteristics for Re=600.Note that the winglets having different aspectratios possess the same surface area.The figure shows that the aspect ratio has a marginal influence on the concentration polarization and pressure.Fig.8 is a plot of area-averaged concentration polarization factor vs.consumed pumping power for various aspectratios.Little influence of aspectratio on concentration polarization is observed.Since σ=2.0 is a typical value for winglet aspect ratio,it is thus taken as the best aspect ratio.
Fig.9 presents the effects of winglet attack angle(β)on concentration polarization and pressure drop characteristics for Re=600.With increasing attack angle,the concentration polarization factor tends to decrease while the pressure drop increases.Fig.10 is a plot of area-averaged concentration polarization factor vs.consumed pumping power for various attack angles.A moderate influence of attack angle on concentration polarization factor is observed,with the winglets having 30°and 40°attack angles yielding a comparably low concentration polarization factor,so either β =30°or β =40°can serve as the best attack angle.Before the selection,let us first see the winglet interval effects,which will be shown in the next two figures.

Fig.3.Solute mass fraction contours on membrane surface for channels without and with delta winglet(Re=600).

Fig.4.Fluid velocity vector plot at cross-section of x/H=6 for channel with delta winglets(Re=600).
Fig.11 shows the effects of winglet interval(W)on concentration polarization and pressure drop characteristics for Re=600.With reducing winglet interval,the concentration polarization factor decreases while the pressure drop increases.Fig.12 is a plot of area-averaged concentration polarization factor vs.consumed pumping power for various winglet intervals.The winglet interval of W=1.0H provides the lowest concentration polarization factor,suggesting that the best interval is W=1.0H.Taking W=1.0H is possible for β =30°but is impossible for β =40°because of the spatial interference between adjacent winglets,so the best attack angle is eventually chosen to be β =30°.
Summary of the above results supports that the optimal geometric parameters for the delta winglets are h=5H/6,σ =2.0,β =30°,and W=1.0H.As compared to the Table 1 data,two parameters are optimized:the winglet height is increased from h=3H/6 to h=5H/6,and the winglet interval is reduced from W=1.5H to W=1.0H.
3.2.Performance comparison of delta winglets with rectangular winglets
As stated early,there are two typical types of winglets including the delta winglet and the rectangular winglet.In our previous research[3],we optimized the rectangular winglets and found that the parameters for the optimal rectangular winglets were h=4H/6,σ =2.0,β =30°,and W=1.5H.It is interesting to compare the present optimal delta winglets with the previous optimal rectangular winglets.Fig.13 indicates that the delta and rectangular winglets yield a comparable concentration polarization factor,but the former gives a slightly greater pressure drop than the latter.Fig.14 shows that for a small pumping power,the delta and rectangular winglets give almost the same concentration polarization factor;for larger pumping powers,however,the former offers a slightly higher concentration polarization factor than the latter.The delta winglets yield a greater pressure drop because they have a more notable channel blocking effect in the present case.If we define the channel blocking rate as the winglet area projected on the channel cross section divided by the channel cross sectional area,we can calculate the blocking rate for the channel with the delta winglets to be(1/2)(5H/6)(2 ×5H/6)sin30°/(H × H)=34.7%,and that with the rectangular winglets to be(4H/6)(2 × 4H/6)sin30°/(H × 1.5H)=29.6%.In spite of this,the delta winglets fail to yield a lower concentration polarization factor than the rectangular winglets.The reason may be that the delta winglets distribute more surface area near the solid wall rather than the membrane as compared with the rectangular winglets.
It is known that the delta winglets are more effective in enhancing heat transfer than the rectangular winglets[19],however,they are not so effective in augmenting mass transfer in the present membrane transport case.A possible explanation is that,when winglets are used in a finned tube heat exchanger,they are set up on the fin surface to enhance the convective heat transfer near the fin surface on which they are mounted;when winglets are employed in a membrane module as in the present case,however,they are placed on the solid wall for augmenting the convective mass transfer near the membrane surface which is opposite to the wall.The present results suggest that knowledge on the heat transfer enhancement by winglets may not be directly applicable to the mass transfer in a membrane channel,special studies are necessary to reveal the regularity of winglet-induced mass transfer enhancement in membrane transports.

Fig.5.Effects of winglet height on concentration polarization and pressure(Re=600).

Fig.6.Area-averaged concentration polarization factor vs.consumed pumping power for various winglet heights(400≤Re≤1000).
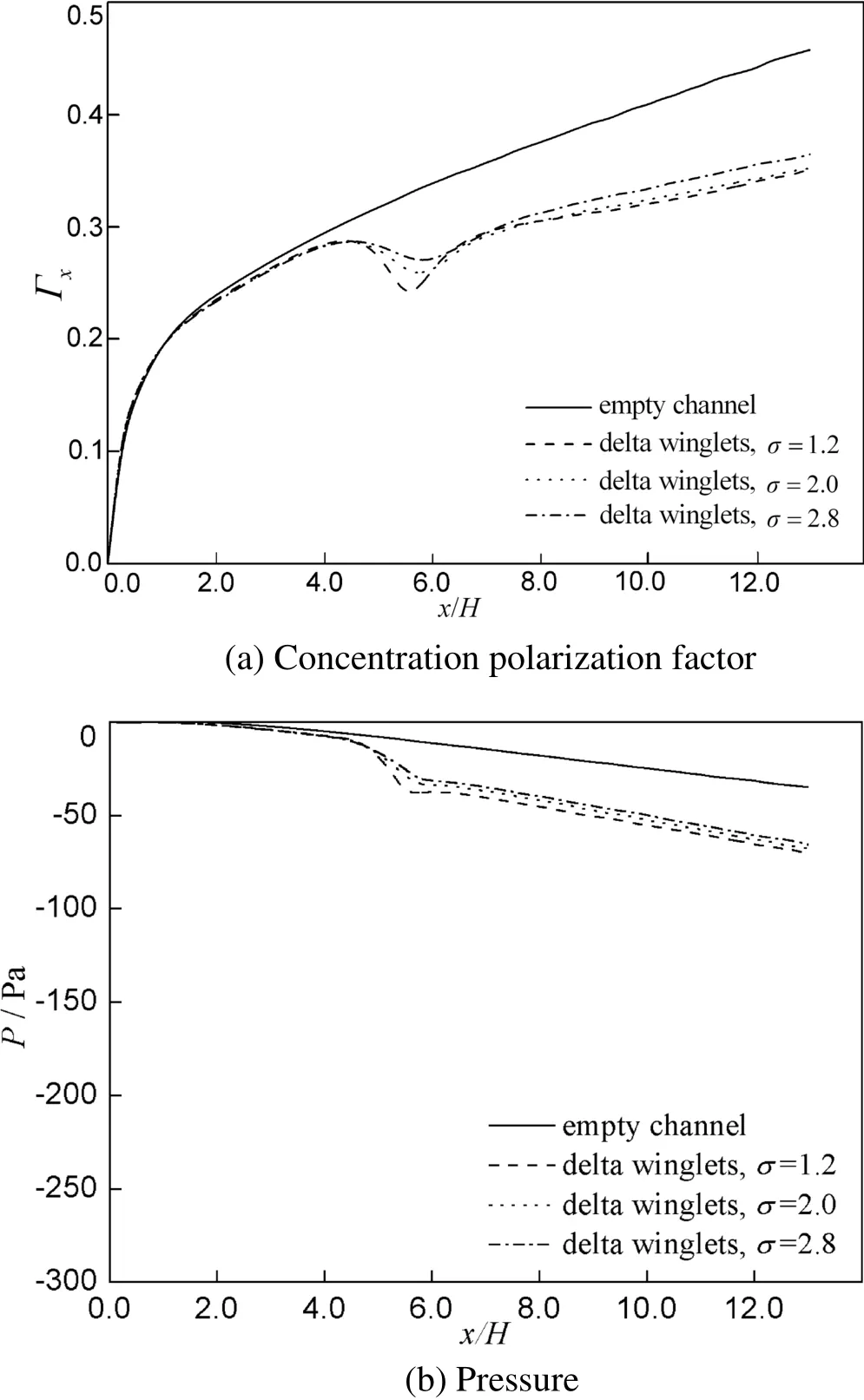
Fig.7.Effects of aspectratio on concentration polarization factor and pressure(Re=600).
4.Conclusions
(1)Numerical calculations were carried out to simulate the solution flow and solute transport in narrow membrane channels with delta winglets.Calculations were implemented to optimize the winglets under equal pumping power condition.

Fig.8.Area-averaged concentration polarization factor vs.consumed pumping power for various aspect ratios(400≤Re≤1000).

Fig.9.Effects of attack angle on concentration polarization factor and pressure(Re=600).

Fig.10.Area-averaged concentration polarization factor vs.consumed pumping powerfor various attack angles(400≤Re≤1000).
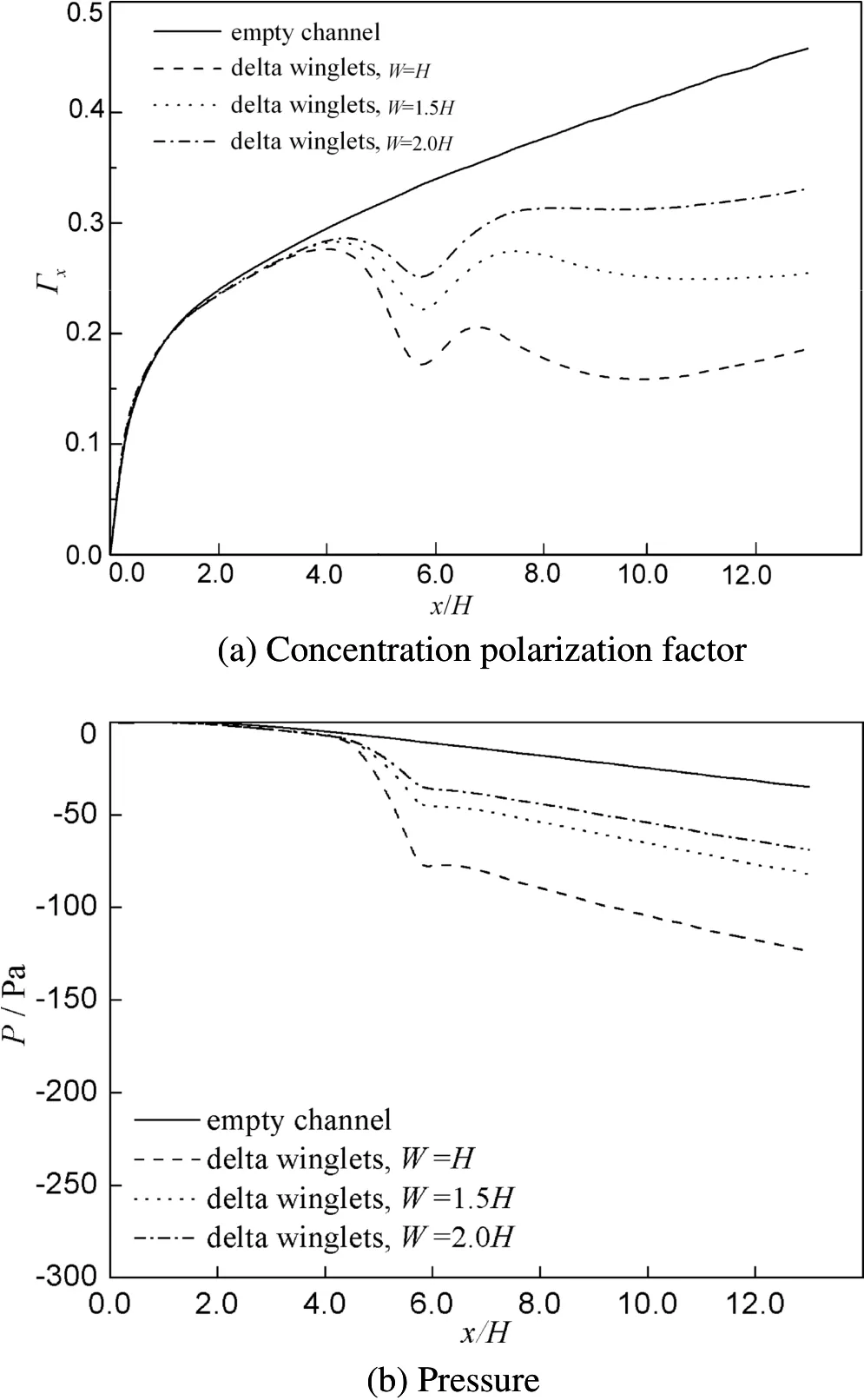
Fig.11.Effects of winglet interval on concentration polarization factor and pressure(Re=600).
(2)Two adjacent delta winglets that form a concave winglet pair generate two counter-rotating vortices and upward flow to wash the membrane surface,which works to reduce the concentration polarization factor,while two adjacent delta winglets that form a convex winglet pair generate two counter-rotating vortices and downward flow to wash the solid wall surface,which acts to increase the concentration polarization factor.

Fig.12.Variations of area-averaged concentration polarization factor with consumed pumping power for various winglet intervals(400≤Re≤1000).

Fig.13.Concentration polarization factor and pressure drop comparisons between optimized delta and rectangular winglets(Re=600).
(3)Parametric optimization of the delta winglets under equal pumping power condition suggests that the winglet height is 5/6 of the channel height,the winglet aspect ratio is 2.0,the winglet attack angle is 30°,and the winglet interval is equal to the channel height.

Fig.14.Area-averaged concentration polarization factor comparison between optimized delta and rectangular winglets(400≤Re≤1000).
(4)The optimal delta winglets and the optimal rectangular winglets show comparable performance.For a small pumping power,they yield almost the same concentration polarization factor;for larger pumping powers,the rectangular winglets give a slightly lower concentration factor than the delta winglets.
Nomenclature
D solute diffusivity,m2·s-1
E pumping power,W
H channel height,m
h winglet height,m
J permeate volume flux across membrane,m·s-1
L channel length,m
l winglet length,m
P pressure,Pa
Re Reynolds number(=2Humρ/μ)
ummean velocity,m·s-1
V volumetric flow rate,m3·s-1
W distance between two adjacent winglets,or width of computational domain,m
w mass fraction,kg·kg-1
x,y,z coordinates,m
β winglet attack angle,(°)
Г concentration polarization factor
ГAarea-averaged concentration polarization factor
Гxlocal concentration polarization factor
μ viscosity,kg·m-1·s-1
ρ density,kg·m-3
σ winglet aspect ratio(=l/h)
Subscripts
0 channel inlet
b bulk flow
p permeate side
w membrane surface
 Chinese Journal of Chemical Engineering2015年11期
Chinese Journal of Chemical Engineering2015年11期
- Chinese Journal of Chemical Engineering的其它文章
- N-methyl-2-(2-nitrobenzylidene)hydrazine carbothioamide—A new corrosion inhibitor for mild steel in 1 mol·L-1 hydrochloric acid
- A dual-scale turbulence model for gas-liquid bubbly flows☆
- Gas-liquid hydrodynamics in a vessel stirred by dual dislocated-blade Rushton impellers☆
- Cobalt-free gadolinium-doped perovskite Gd x Ba1-x FeO3-δas high-performance materials for oxygen separation☆
- Synthesis and adsorption property of zeolite FAU/LTA from lithium slag with utilization of mother liquid☆
- Simulation and analysis of multi-stage centrifugal fractional extraction process of 4-nitrobenzene glycine enantiomers☆
