A Note on Zinbiel Algebras

Ni Jun-na

（School of Mathematical Sciences，South China Normal University，Guangzhou，510631）

Communicated by Du Xian-kun

A Note on Zinbiel Algebras

Ni Jun-na

（School of Mathematical Sciences，South China Normal University，Guangzhou，510631）

Communicated by Du Xian-kun

In this paper，we consider the decomposition of Zinbiel algebras with a special bilinear form which are called quadratic Zinbiel algebras.We obtain that the decomposition into irreducible ideals of a quadratic Zinbiel algebra is unique under an isometry.

Zinbiel algebra，quadratic，decomposition，isometry

2010 MR subject classification：17A30，17A32

Document code：A

Article ID：1674-5647（2015）03-0261-06

1　Introduction

Lie algebra is one of the important object of the modern theory of non-associative algebras. Active investigations in the theory of Lie algebras lead to the appearing of some generalizations of these algebras such as Malcev algebras，Lie superalgebras，binary Lie algebras，Leibniz algebras and so on.Recall that Leibniz algebras are defined by the following identity

The category of Zinbiel algebras is Koszul dual to the category of Leibniz algebras in the sense of Loday［1］.So Zinbiel algebras are also called dual Leibniz algebras（see［2］）.

A Zinbiel algebra is a vector space A together with a bilinear map◦：A×A→A such that

One can get a commutative associative algebra structure on A under the new defined product x◦y+y◦x.

Zinbiel algebras have a close relationship with dendriform algebras，pre-Lie algebras，etc.（see［3-4］）.We recall their definitions in the following.

A pre-Lie algebra is a vector space A together with a bilinear map·：A×A→A such that

It is well known that A becomes a Lie algebra under the new defined product x·y-y·x.

A dendriform algebra is a vector space A with two bilinear products denoted by≺and≻.If for any x，y，z∈A，then the following equalities hold：

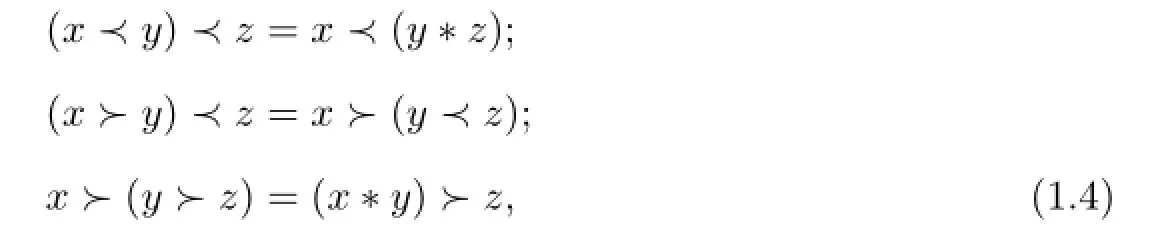
where x∗y=x≺y+x≻y.Define a new product⋆：A×A→A by x⋆y=x≺y+x≻y，then A becomes an associative algebra.

As a commutative algebra is an associative algebra for which x◦y=y◦x，a Zinbiel algebra may be equivalently defined as a dendriform algebra for which x≻y=y≺x. If one thinks of dendrifrom algebras as an analog of associative algebras，then one views Zinbiel and pre-Lie algebras as the“dendriform analog”of commutative and Lie algebras，respectively.The situation is summarized by means of the following diagram，where one thinks of the rows as“exact sequences”（see［3，5］）：

Also Zinbiel algebra is concerned with pre-Poisson algebras.It is shown that the free Zinbiel algebra（the shuffle algebra）on a pre-Lie algebra is a pre-Poisson algebra（see［5］）.So Zinbiel algebra is a kind of important algebra structure as well as associative or Lie algebras and so on.The study of Zinbiel algebras is obviously difficult due to the non-associativity. In spite of some progress（see［6-12］），there are still many open questions.

However，there is very few study about the decomposition on Zinbiel algebras.In this paper，we investigate the decomposition of Zinbiel algebras with a associative bilinear form. A bilinear form f：A×A→C is associative if and only if

The goal of this paper is to study the pair（A，f），where A denotes a Zinbiel algebra and f denotes a non-degenerate associative symmetric bilinear form on A.In abuse of notation we also use the term quadratic Zinbiel algebra for denoting such a pair.The motivation for studying quadratic Zinbiel algebras comes from the fact that Lie or associative algebras with forms have important applications in several areas of mathematics and physics，such as the structure theory of finite-dimensional semi-simple Lie algebras，the theory of complete integrable Hamiltonian systems and the classification of statistical models over two-dimensional graphs.

Throughout this paper，all algebras are finite-dimensional and over the complex field C.

2　Preliminaries

In this section，we give the definitions and some results for Zinbiel algebras in order to make this paper as self-contained as possible.

Suppose that（A，f）is a quadratic Zinbiel algebra.For a Zinbiel algebra A，the anticommutator

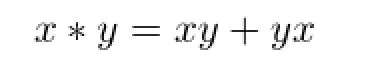
defines a commutative associative algebra B=B（A），which is called the sub-adjacent algebra of A.

An ideal I of a Zinbiel algebra A satisfies IA⊆I and AI⊆I.Let H⊆A.Then the centralizer of H in A is the set CA（H）=｛x∈A|xH=Hx=0｝.If H is an ideal of A，then so is CA（H）.In particular，if H=A，then C（A）=CA（A）is called the center of A.

As usual，a Zinbiel algebra A is said to be solvable if A（k）=0 for some integer k，where A（i）are defined by

Similarly，A is nilpotent if Ak=0 for some integer k，where

Let I be an ideal of quadratic（A，f）.I is nondegenerate if f|I×Iis nondegenerate，and is isotropic if f|I×I=0.We say that（A，f）is irreducible if the nondegenerate ideal of A is 0 or A.

The following well known result is always used in our discussions.

Lemma 2.1Let（A，f）be a quadratic Zinbiel algebra.

（1）（AA）⊥is the center C（A）of A；

（2）Let I be an ideal of A.Then I⊥is also an ideal of A.Furthermore，assume that I is nondegenerate.Then I⊥is also nondegenerate and A=I⊕I⊥.

An automorphism π of（A，f）is called an isometry if π preserves the bilinear form，i.e.，

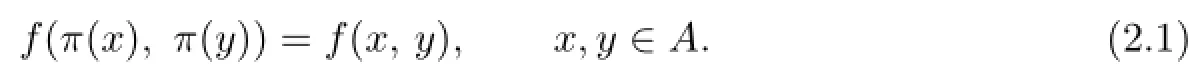
3　Decomposition Theorems of Quadratic Zinbiel Algebras

We firstly consider the abelian quadratic Zinbiel algebras.

Theorem 3.1Let（A，f）be an abelian quadratic Zinbiel algebra.Then the orthogonal decomposition of A into nondegenerate irreducible ideals is unique up to an isometry.

Proof.Since that（A，f）is abelian，any irreducible ideal of（A，f）is one-dimensional.

Then if A have the following two decompositions：

where Cai（i=1，2，···，t），Cbj（j=1，2，···，m）are one-dimensional ideals of A and f（ai，ai）/=0，f（bi，bi）/=0.We get that t=m by the dimension of A.

For convenience，we can choose ai，bisuch that f（ai，ai）=1，f（bi，bi）=1.Then the map ai-→bi，i=1，···，t is the isometry.

According to Theorem 3.1，the decomposition of abelian quadratic Zinbiel algebras into nondegenerate irreducible ideals is easy.Then，we turn to the nonabelian quadratic Zinbiel algebra for the decomposition.

Theorem 3.2Let（A，f）be a nonabelian quadratic Zinbiel algebra with a nonisotropic center.Then there is an orthogonal decomposition A=Aa⊕Abof A，where Aais a nondegenerate abelian ideal and Abis an ideal with an isotropic center.

Proof.Since C（A）is nonisotropic，there exist x，y∈C（A）such that f（x，y）/=0.This implies that there is an element z∈C（A）such that f（z，z）/=0.So V=Cz is nondegenerate ideal in C（A）.

Since dimC（A）＜∞，there exists a maximal nondegenerate ideal in C（A），denoted by Aa.LetThen there is an orthogonal decomposition

Furthermore，C（Ab）is isotropic.In fact，if C（Ab）is nonisotropic，then there is d∈C（Ab）such that f（d，d）/=0.Hence Aa⊕Cd is nondegenerate，which contradicts the maximality of Aa.Then the theorem is proved.

By Theorem 3.2，the quadratic Zinbiel algebras with isotropic centers play an important role.

Lemma 3.1Let（A，f）be a quadratic Zinbiel algebra with an isotropic center.Assume that A has a decomposition A=H1⊕H2，where H1and H2are ideals of A.Then bothandare nondegenerate.

Let（A，f）be a quadratic Zinbiel algebra with an isotropic center and

be decompositions of A，where Hi，H′j，1≤i≤n，1≤j≤m are nondegenerate irreducible ideals of A.

Lemma 3.2Let the notations be as above.ThenandProof.Letand.It is obvious that B and B′are ideals of H1.

（1）If H1=B⊕B′，then B and B′are nondegenerate by Lemma 3.1.Since H1is irreducible，one of B and B′must be zero.By the assumption，we have B′=0.

（2）If H1/=B⊕B′，we may choose an element d∈H1but d∈/B⊕B′.LetwhereBy using the other decomposition，we have

So

本文首先采用因子分析法来选取影响人口老龄化的指标。因子分析法有利于从众多的观测指标中选取若干重要指标，用少数独立的观测变量来表示其基本的数据结构，以此来获得各观测指标与所研究的指标之间的相关关系。因子分析可以达到数据简化的目的，因此其应用极为广泛。

It follows that

It is easy to see that

If d1/∈B⊕B′，assume that B1=B⊕Cd1andif d2/∈B⊕B′，assume that B1=B andIt follows from the identities（3.1）and（3.2）that B1and B′1are ideals of H1.

Lemma 3.3Let the notations be as above.Define π1by the projection π1：

Then π1is an isomorphism and preserves the bilinear form f.

Let x=x1+x2and y=y1+y2，where xand.By Lemma 3.2，we have

Similarly，we get Ax2=0.Thus we obtain x2∈C（A）.Similarly，we obtain y2∈C（A）.

Then z1∈C（A）sincend Az1=0.Then

for the center of A is isotropic.Similarly，f（x2，y1）=0.It follows that

From Lemmas 3.2 and 3.3，we have

Repeating the above discussion for i=2，3，···，n，we have the following theorem.

Theorem 3.3Let（A，f）be a quadratic Zinbiel algebra with an isotropic center，and

be two decompositions of A，where Hi，are nondegenerate irreducible ideals of A.Then we have

（1）n=m；

（2）changing the subscripts if necessary，we have dimand

（3）the projections πjare isomorphisms and preserve the bilinear form.So π=（π1，···，πn）is an isomorphism of A.

References

［1］Loday J L.Cup product for Leibniz cohomology and dual Leibniz algebras.Math.Scand.，1995，77：189-196.

［2］Loday J L.Dialgebras，in dialgebras and related operads.Lecture Notes in Math.，2001，1763：7-66.

［3］Chapoton F.Un th´er`eme de Cartier-Milnor-Moore-Quillen pour les big`ebres dendriformes et les alg`ebres braces.J.Pure Appl.Algebra，2002，168（1）：1-18.

［4］Ronco M.Primitive elements in a free dendriform algebra.Contemp.Math.，2000，267：245-263.

［5］Aguiar M.Pre-Poisson algebras.Lett.Math.Phys.，2000，54（4）：263-277.

［6］Dzhumadil'daev A S.Identities for Multiplications Derived by Leibniz and Zinbiel Multiplications.Abstracts of Short Communications of International Conference“Operator algebras and quantum theory of probability”.Tashkent，2005：76-77.

［7］Dzhumadil'daev A S，Tulenbaev K M.Nilpotency of Zinbiel algebras.J.Dyn.Control Syst.，2005，11（2）：195-213.

［8］Adashev J Q，Omirov B A，Khudoyberdiyev A Kh.Classifications of some classes of Zinbiel algebras.arXiv：math/0702809v1［math.RA］.Submitted on 27 Feb.2007.

［9］Adashev J Q，Khuhoyberdiyev A Kh，Omirov B A.Classification of complex naturally graded quasi-filiform Zinbiel algebras.arXiv：0805.3072v1［math.RA］.Submitted on 20 May 2008.

［10］Ioannis D.Zinbiel algebras and commutative algebras with divided powers.Glasg Math.J.，2010，52（2）：303-313.

［11］Camacho L M，Ca~nete E M，G´omez-Vidal S，Omirov B A.p-Filiform Zinbiel algebras.Linear Algebra Appl.，2013，438（7）：2958-2972.

［12］Ni J N.Centroids of Zinbiel algebras.Comm.Algebra，2014，42：1844-1853.

10.13447/j.1674-5647.2015.03.08

date：Dec.3，2013.

E-mail address：nijunna@126.com（Ni J N）.