A Class of Schur Convex Functions and Several Geometric Inequalities

Wang Wen anD Yang Shi-guo

（School of Mathematics and Statistics，Hefei Normal University，Hefei，230601）

Communicated by Rong Xiao-chun

A Class of Schur Convex Functions and Several Geometric Inequalities

Wang Wen anD Yang Shi-guo

（School of Mathematics and Statistics，Hefei Normal University，Hefei，230601）

Communicated by Rong Xiao-chun

Schur convexity，Schur geometrical convexity and Schur harmonic convexity of a class of symmetric functions are investigated.As consequences some known inequalities are generalized.In addition，a class of geometric inequalities involving n-dimensional simplex in n-dimensional Euclidean space Enand several matrix inequalities are established to show the applications of our results.

Schur convex function，Schur geometrically convex function，Schur harmonically convex function，simplex，geometric inequality

2010 MR subject classification：05E05，26B25，52A40

Document code：A

Article ID：1674-5647（2015）03-0199-12

1　Introduction

The Schur convex function was introduced by Schur［1］in 1923 and played a key role in analytic inequalities（see［2-17］）.Moreover，the theory of convex functions and Schur convex functions is one of the most important research fields in modern analysis and geometry.The following definitions can be found in many references such as［1-3，14-15］.

Definition 1.2A real-valued function f：Ω⊂Rn→R is said to be Schur convex on Ωif

f is a Schur concave function on Ω if and only if-f is a Schur convex function.

The following lemma is so-called Schur's condition for determining whether or not a given function is Schur convex or Schur concave.

Lemma 1.1［1，P57］Let Ω∈Rnbe a symmetric and convex set with nonempty interior，and let f：Ω→R be differentiable in the interior of Ω.Then f is Schur convex（Schur concave）on Ω if and only if f is symmetric on Ω and

where Ω0is the interior of Ω.

The multiplicatively convex function was recommended by Niculescu［10］，which revealed an entire new world of graceful inequalities.Zhang［17］stated the Schur geometrically convex theory as a parallel one to Schur convex theory by defining logarithmic majorization and using multiplicatively convex function.

Definition 1.3［17，P89］Assume that x and y are two n-tuples of nonnegative numbers. Then the n-tuple x is called logarithmically majorized by y（in symbols lnx≺lny）if

Definition 1.4［17，P107］Suppose that I is a subinterval of（0，∞）.A function φ：In→（0，∞）is called Schur geometrical convexity if

φ is called Schur geometrically concave if-φ is Schur geometrically convex.

The following Lemma is basic and plays a fundamental role in the theory of Schur geometrically convex function.

Lemma 1.2［17，P108］Let φ（x）=φ（x1，x2，···，xn）be symmetric and have continuously partial derivatives on In，where I is a subinterval of（0，∞）.Then φ：In→ （0，∞）is Schur geometrically convex（Schur geometrically concave）if and only if

Definition 1.5Let ω（x）=ω（x1，x2，···，xn）be symmetric and have continuously partial derivatives on In，where I is a subinterval of（0，∞）.Then ω：In→ （0，∞）is a Schur harmonic convex function if

Lemma 1.3［5］Let ω（x）=ω（x1，x2，···，xn）be symmetric and have continuously partial derivatives on In，where I is a subinterval of（0，∞）.Then ω：In→ （0，∞）is Schur harmonic convex（Schur harmonic concave）if and only if

In what follows，we denote by a，b，c the sides of the triangle△ABC in Euclidean plane. Let hi，ri（i=1，2，3），r be the altitudes，the radii of excircles and the radii of incircles，respectively.The following geometric inequalities are known（see［18］）.

In this paper，we investigate the Schur convexity，Schur geometrical convexity and Schur harmonic convexity of the following symmetric functions：

where 0≤xi＜1，α≥1，λ∈R and k=1，2，···，n（≥2）.As consequences several interesting inequalities are established.As applications，several interesting geometric inequalities involving n-dimensional simplex in n-dimensional Euclidean space Enare established. Those results are generalizations of（1.4）-（1.7）.In addition，we also obtain several matrix inequalities.

2　Schur Convexity of Some Symmetric Functions

In this section，we investigate the Schur convexity（concave）of some symmetric functions and establish several analytic inequalities.

Theorem 2.1For α≥ 1，the functionis Schur convex on［0，1）nwhen λ∈（0，1］and Schur concave on［0，1）nwhen λ∈［-1，0）.

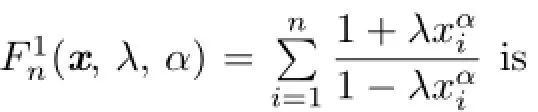
Thus，one has

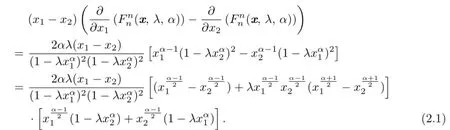
It follows from the function xr（r＞0）is increasing in（0，+∞）with

Therefore，if λ∈（0，1］，from（2.1）and（2.2），we clearly see that

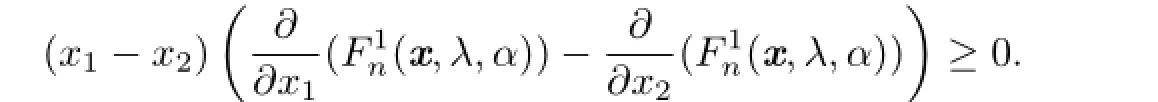
Together with Lemma 1.3 imply that the functionis Schur convex on［0，1）n.

On the other hand，for λ∈［-1，0），from（2.1）and（2.2），we get

Theorem 2.2For 2≤k≤n and α≥1，the function（x，λ，α）is Schur convex on［0，1）nwhen λ∈（0，1］and Schur concave on［0，1）nwhen λ∈［-1，0）.

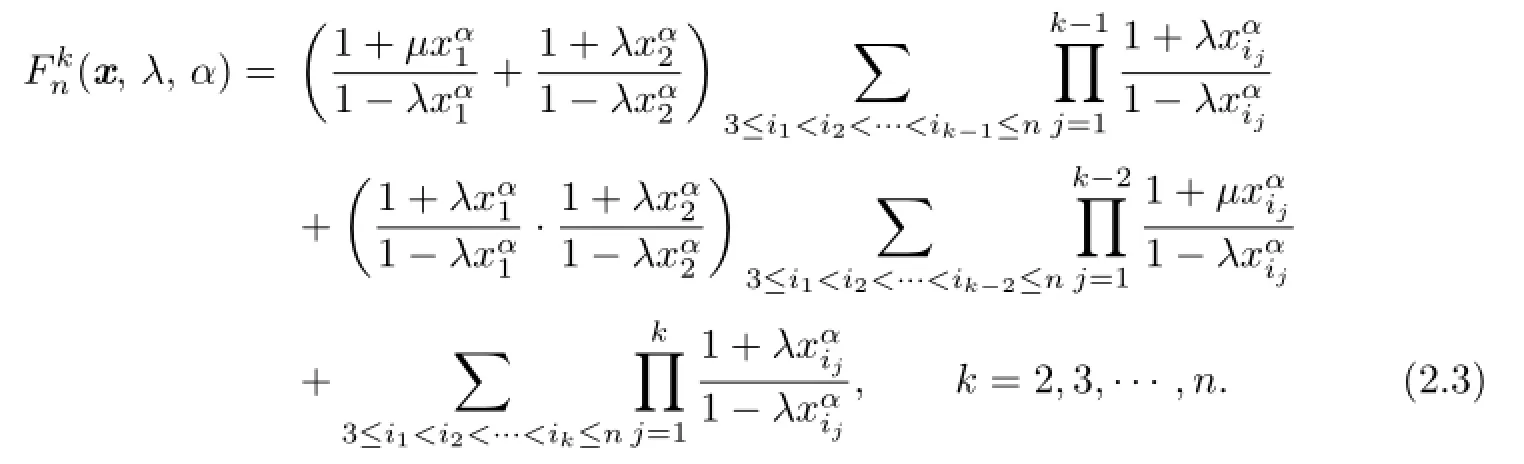
For k=2，we set

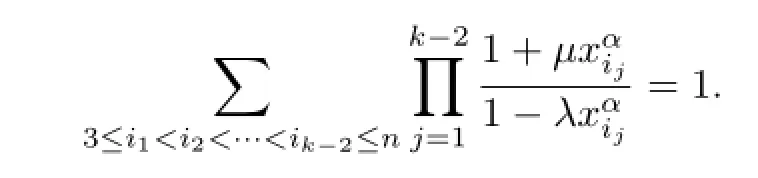
where

Combining（2.4）with（2.5），we obtain

Therefore，when λ∈（0，1］，from（2.2）and（2.6），we have

On the other hand，when λ∈［-1，0），from（2.2）and（2.6），it is not difficult to find that

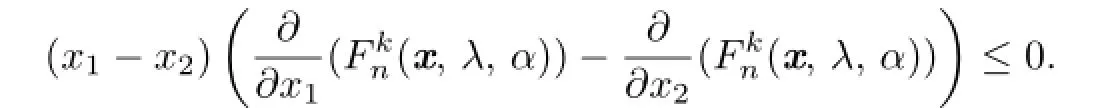
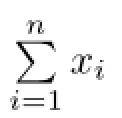
if λ∈［-1，0），then

3　Schur Geometrical Convexity and Schur Harmonic Convexity of（x，λ，α）

In this section，we prove the function（x，λ，α）（1≤k≤n）to be Schur geometrically convex and Schur harmonic convex on（0，1］n.

Theorem 3.1For α≥1 and 1≤k≤n，the function（x，λ，α）is Schur geometrically convex on［0，1）nwhen λ∈（0，1］and Schur geometrically concave on［0，1）nwhen λ∈［-1，0）.

Proof.It follows from（2.4）and（2.5）that

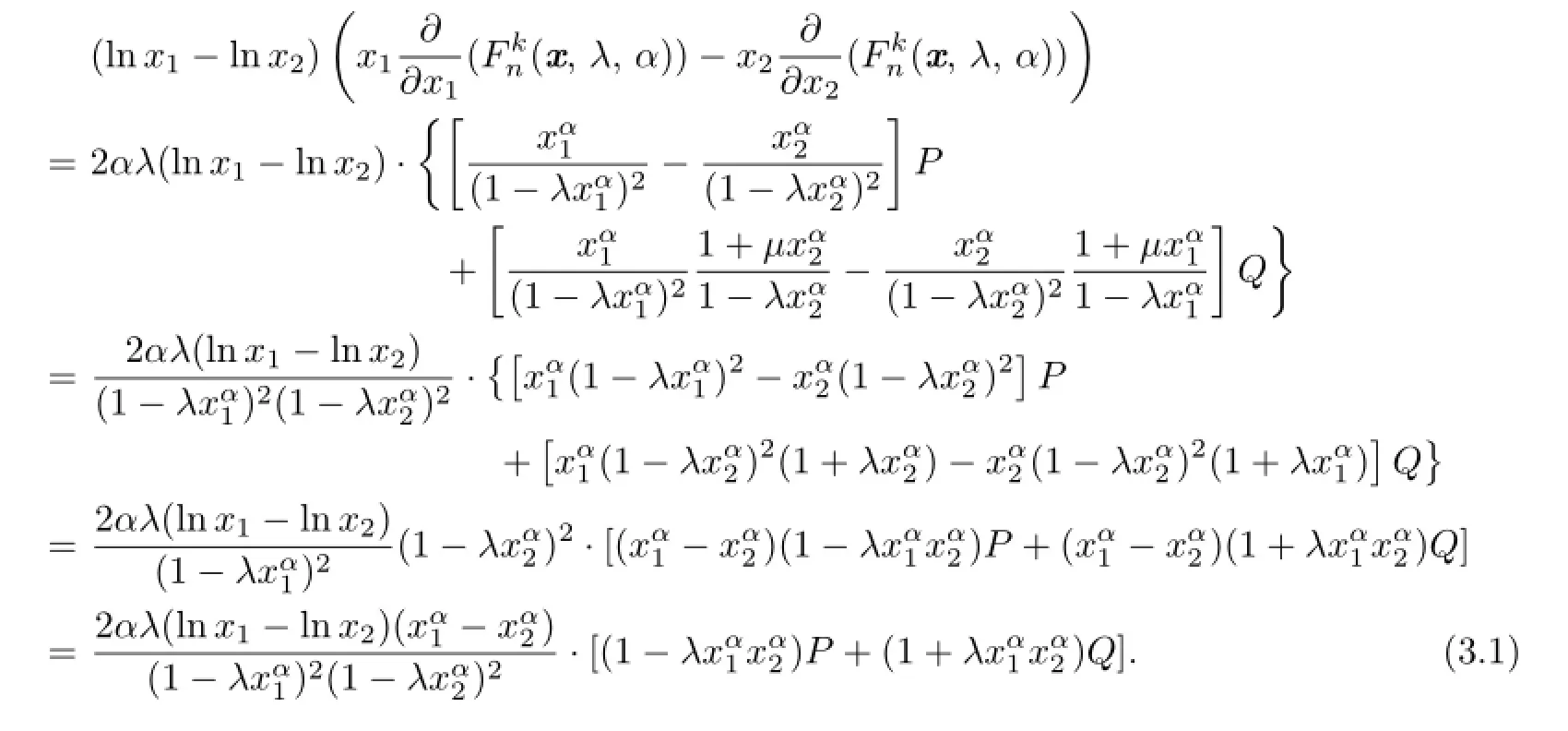
Using（2.2）and（3.1），for λ∈（0，1］，we find

Similarly，if λ∈［-1，0），then the function（x，λ，α）is Schur geometrically concave on［0，1）n.So the proof is completed.

The following results holds in terms of Theorem 3.1 and the fact that ln（s，s，···，s）≺ln（x1，x2，···，xn）（see page97 in［17］）.

Corollary 3.1Let α≥1.For λ∈（0，1］，we have

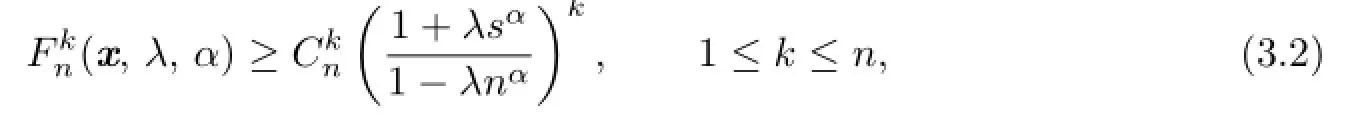
and for λ∈［-1，0），we have

Theorem 3.2For α≥1 and 1≤k≤n，the function（x，λ，α）is Schur harmonic convex on［0，1）nas λ∈（0，1］and Schur harmonic concave on［0，1）nas λ∈［-1，0）.

Proof.From（2.4）and（2.5）we find

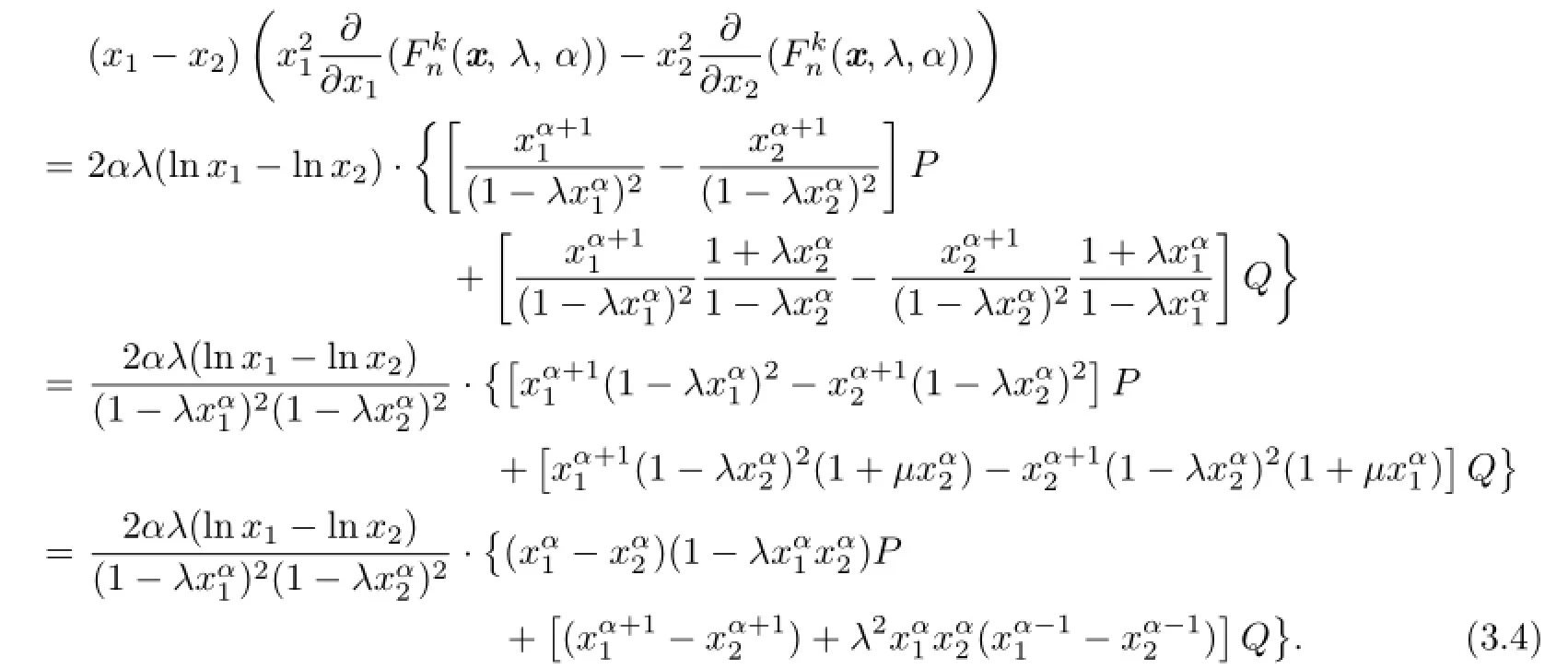
By using（2.2）and（3.4），for λ∈（0，1］，we have

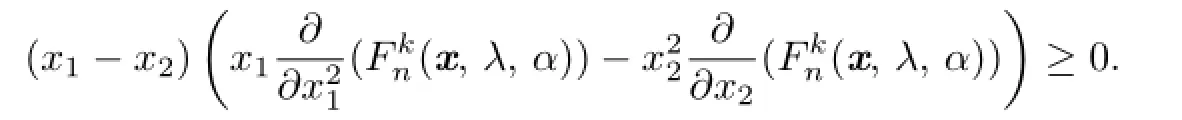
Similarly，if λ∈［-1，0），then the function（x，λ，α）is Schur harmonic concave on［0，1）n.

if λ∈［-1，0），then

Proof.It is easy to find that

(

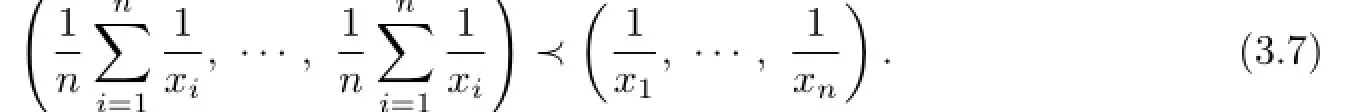
Thus，from Definition 1.7，Theorem 3.3 and（3.7），（3.5）and（3.6）hold.

4　Some Applications

4.1Several Geometric Inequalities

Let Ω =｛A1，A2，···，An+1｝be an n-dimensional simplex in n-dimensional Euclidean space En（n≥2）with V the volume.We denote by hi，ri，Fi（i=1，2，···，n+1）and r the altitudes，the radii of excircles，the areas of lateral surfaces and the radii of incircles of Ω，respectively.A large number of geometric inequalities involving n-simplex have been presented（see［18-26］）.

We first give a lemma.

Lemma 4.1Let Ω=｛A1，A2，···，An+1｝be an n-dimensional simplex in n-dimensional Euclidean space En（n≥2）.The following relations are valid：

(

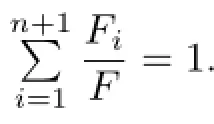
Applying Lemma 4.1 and the main results in Sections 2 and 3，we can establish some interesting geometric inequalities on n-dimensional simplex in n-dimensional Euclidean space En.

Theorem 4.1Let Ω=｛A1，A2，···，An+1｝be an n-dimensional simplex in n-dimensional Euclidean space En（n≥2）.For α≥1，if λ∈（0，1］，then

if λ∈［-1，0），then

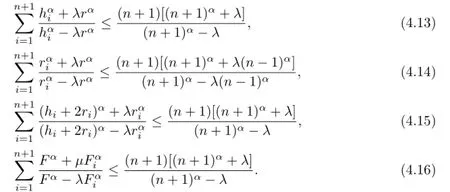
The equalities hold if and only if the n-simplex Ω is regular.

Proof.From Theorem 2.1 and Definition 1.2，and by using（4.1）-（4.4），respectively，we obtain（4.9）-（4.16）.

Theorem 4.2Let Ω=｛A1，A2，···，An+1｝be an n-dimensional simplex in n-dimensional Euclidean space En（n≥2）.For α≥1，if λ∈（0，1］，then

if λ∈［-1，0），then

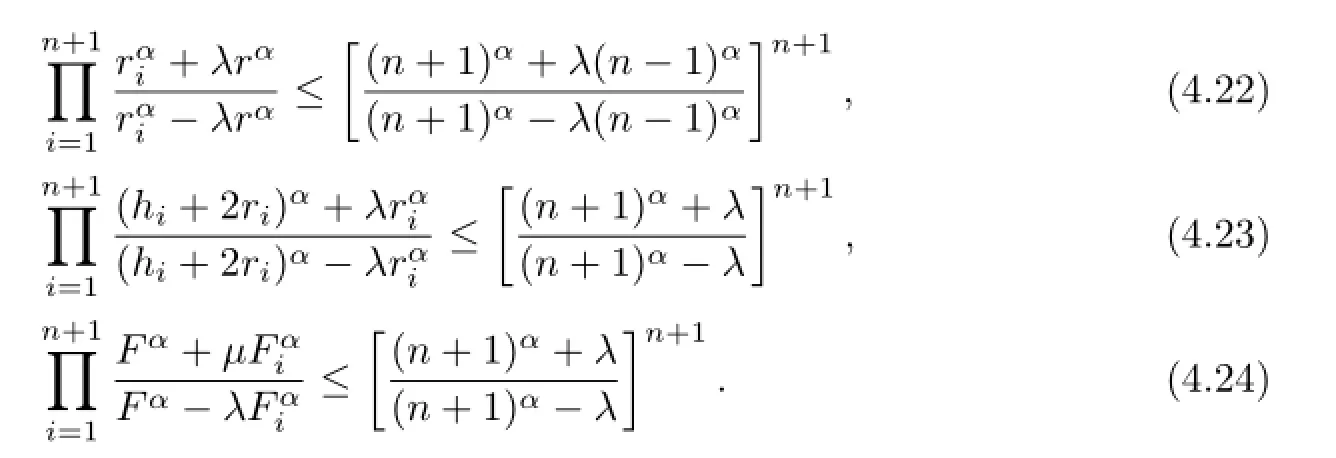
Equalities hold if and only if the n-simplex Ω is regular.

Proof.From Theorem 2.2 and Definition 1.2，and by using（4.1）-（4.4），respectively，we can get（4.17）-（4.24）.

Theorem 4.3Let Ω=｛A1，A2，···，An+1｝be an n-dimensional simplex in n-dimensional Euclidean space En（n≥2）.For a given point P in Ω，let Bistand for the intersection point of straight line AiP and hyperplane ai=A1···Ai-1Ai+1···An+1.For α≥1，if λ∈（0，1］，then

if λ∈［-1，0），then

Proof.By using Theorems 2.1 and 2.2，respectively，we can immediately obtain（4.25）and（4.26）.

In fact，from Theorem 2.2，and by using（4.1）-（4.4），we find the following more generally inequalities.

Theorem 4.4Let Ω=｛A1，A2，···，An+1｝be an n-dimensional simplex in n-dimensional Euclidean space En（n≥2）.For α≥1，if λ∈（0，1］，then

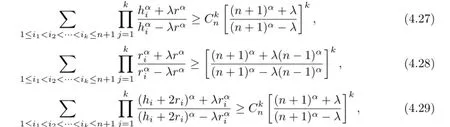
if λ∈［-1，0），then

The equalities hold if and only if the n-simplex Ω is regular.

4.2Matrix Inequalities

Let A=（aij）n×nis a complex matrix.Let

where the componentsµiand σi，i=1，2，···，n，are eigenvalues and singular values of A，respectively.

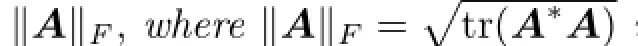
if λ∈［-1，0），then

Proof.The fact in［8］reads as follows：

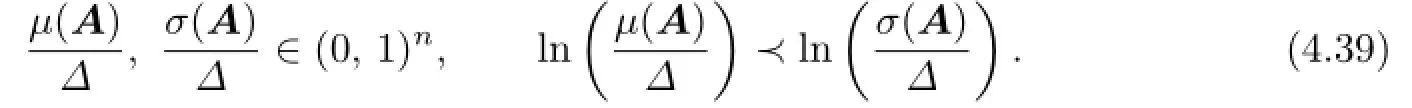
Thus，（4.37）and（4.38）are deduced from（4.39）and Theorem 3.3.

References

［1］Marshall A W，Olkin I.Inequalities：Theory of Majorization and Its Applications.New York：Academic Press，1979.

［2］Hardy G H，Littlewood J E，P´olya G.Some simple inequalities satisfied by convex functions. Messenger Math.，1929，58：145-152.

［3］Wang B Y.Foundations of Majorization Inequalities（in Chinese）.Beijing：Beijing Normal Univ.Press，1990.

［4］Chu Y M，Xia W F，Zhao T H.Schur convexity for a class of symmetric functions（in Chinese）. Sci.China Ser.A，2010，53（2）：465-474.

［5］Chu Y M，Sun T C.The schur harmonic convexity for a class of symmetric functions.Acta Math.Sci.，2010，B30（5）：1501-1506.

［6］Xia W F，Chu Y M.The Schur convexity and inequalities for a class of symmetric functions（in Chinese）.Acta Math.Sci.，2012，A32（1）：80-89.

［7］Guan K Z.A class of symmetric functions for multiplicatively convex function.Math.Inequal. Appl.，2007，10（4）：745-753.

［8］Guan K Z.Some properties of a class of symmetric functions.J.Math.Anal.Appl.，2007，336：70-80.

［9］Guan K Z，Shen J.Schur-convexity for a class of symmetric function and its applications. Math.Inequal.Appl.，2006，9：199-210.

［10］Niculescu C P.Convexity according to the geometric mean.Math.Inequal.Appl.，2000，3（2）：155-167.

［11］Shi H N，Wu S，Qi F.An alternative note on the Schur-convexity of the extended mean values. Math.Inequal.Appl.，2006，9（2）：219-224.

［12］Yang Z H，Necessary and sufficient conditions for Schur geometrical convexity of the fourparameter homogeneous means.Abstr.Appl.Anal.，2010：Article ID 830163，16 pages，doi：10.1155/2010/830163.

［13］Qi F，S´andor J，Dragomir S S.Notes on the Schur-convexity of the extended mean values. Taiwanese J.Math.，2005，9：411-420.

［14］Mitrinovi´c E S.Analytic Inequalities.New York：Springer-Verlag，1970.

［15］Peˇcari´c J，Proschan F，Tong Y L.Convex Functions，Partial Orderings，and Statistical Applications.New York：Academic Press，1992.

［16］Kuang J C.Applied Inequalities（in Chinese）.3rd ed.Jinan：Shangdong Science and Technology Press，2004.

［17］Zhang X M.Geometrically-convex Functions（in Chinese）.Hefei：Anhui Univ.Press，2004.

［18］Zun S.Geometric Inequalities（in Chinese）.Shanghai：Shanghai Education Press，1980.

［19］Mitrinovi´c D S，Peˇcari´c J E，Volenec V.Recent Advances in Geometric Inequalities.Dordrecht-Boston-London：Kluwer Acad.Publ.，1989.

［20］Zhang J Z，Yang L.A class of geometric inequalities concerning the mass-points system（in Chinese）.J.China Univ.Sci.Technol.，1981，11：1-8.

［21］Leng G S，Ma T Y，Qian X Z.Inequalities for a simplex and an interior point.Geom.Dedicata，2001，85：1-10.

［22］Yang S G，Wang W.The n-dimsensional Pedoe inequality in hyperbolic space with applications（in Chinese）.Advances Math.，2012，43（3）：347-355.

［23］Yang S G，Wang W.The Neuberg-Pedoe inequality in the spherical space（in Chinese）.Acta Math.Sci.，2011，A31（5）：1282-1289.

［24］Xiao J Z，Zhu X H.Schur convex functions and inequalities of n-simplex（in Chinese）.Appl. Math.J.Chinese Univ.Ser.A，2001，16（4）：428-434.

［25］Wang W，Yang S G.Generalization of n-dimensional Pedoe inequality in Euclidean space（in Chinese）.J.Univ.Sci.Technol.China，2012，42（11）：913-919.

［26］Wang W，Yang S G.Generalizations of Euler inequality in n-dimensional Euclidean space. Chinese Quart.J.Math.，2012，27（2）：218-223.

10.13447/j.1674-5647.2015.03.02

date：July 25，2013.

The Doctoral Programs Foundation（20113401110009）of Education Ministry of China，the Natural Science Research Project（2012kj11）of Hefei Normal University，and the NSF（KJ2013A220）of Anhui Province.

E-mail address：wenwang1985@163.com（Wang W）.