Multilinear Fractional Integral Operators on Morrey Spaces with Variable Exponent on Bounded Domain

Wang Min，Qu Meng anD Shu Li-sheng

（School of Mathematics and Computer Science，Anhui Normal University，Wuhu，Anhui，241003）

Communicated by Ji You-qing

Multilinear Fractional Integral Operators on Morrey Spaces with Variable Exponent on Bounded Domain

Wang Min，Qu Meng anD Shu Li-sheng*

（School of Mathematics and Computer Science，Anhui Normal University，Wuhu，Anhui，241003）

Communicated by Ji You-qing

We prove the boundedness of multilinear fractional integral operators on products of the variable exponent Morrey spaces on bounded domain.

multilinear fractional integral operator，variable exponent Morrey space，bounded domain

2010 MR subject classification：46E30，42B20

Document code：A

Article ID：1674-5647（2015）03-0253-08

1　Introduction

Let Ω be an open set in the n-dimensional Euclidean space Rnwith|Ω|＞0，and

be the m-fold product space of Ω.The multilinear fractional integrals on Ω are defined by

Theorem 1.1［7］Suppose that m∈N，0＜β＜mn，

and

with 1＜pi≤qi＜∞for i=1，2，···，m.Then there exists a constant C＞0 such that

In this article，our main aim is to extend one of Tang's work to the variable exponent case.In recent twenty years，variable exponent spaces have been generating interest because of its connection with the study of variational integrals and partial differential equations with a non-standard growth condition（see［8-9］）.

We first recall the definitions of Lebesgue spaces with variable exponent Lp（·）（Ω）（see［10］）.

Let p（·）：Ω→［1，∞）be a measurable function.The variable exponent Lebesgue space Lp（·）（Ω）is defined by

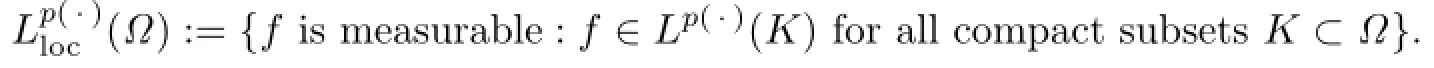
We denote

Let P（Ω）be the set of measurable function p（·）on Ω with value in［1，∞）such that

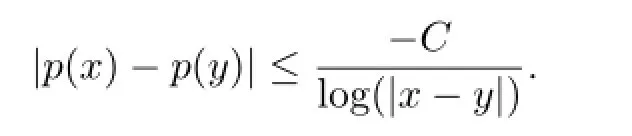
We say that p（·）is log-H¨older continuous at infinity，and denote this by p（·）∈LH∞，if there exists a constant C such that for all x，y∈Ω，|y|≥|x|，

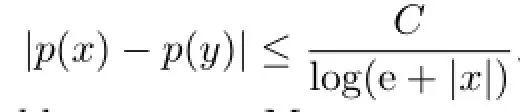
Next we introduce the variable exponent Morrey spaces.

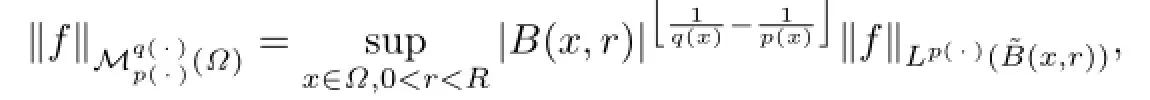
where R：=diam（Ω），B˜（x，r）=B（x，r）Ω.

It is easy to see that if p（·）=q（·），thenWhen p（x）≡p and q（x）≡q are constants，the spacecoincides with the classical Morrey space

The following theorem is the extension of Tang's result（see［7］）to variable exponent case where Ω is a bounded domain.

and

Remark 1.1Almeida et al.［12］obtained the boundedness of Iβon variable exponent Morrey space on a bounded domain，even β is variable.Theorem 1.2 is just the corresponding result of［12］，where m=1 and β is a constant.Recently，Ho［13］studied the boundedness of Iβon Morrey space with variable exponent on unbounded domains，which indicates that Theorem 1.2 is corrected when m=1 for global case.

It is an interesting problem that whether Theorem 1.2 can be extended to global case for m＞1.We also note that our proof of Theorem 1.2 share some ideas of［7］，［14］and references therein.Tao et al.［14］obtained the boundedness of multilinear Calder´on-Zygmund operators on variable exponent Morrey spaces over domains.

2　Proof of Theorem 1.2

In order to prove our result，we need some conclusions as follows.

Lemma 2.1［12］Let Ω be a bounded domain，p（·）∈P（Ω）and p（·）∈LH0.Then

with C＞0 independent of x∈Ω and r＞0.

Lemma 2.2［10］If p（·）∈P（Ω），then for alland all，we have

where

Lemma 2.3［15］Let p（·），p1（·），p2（·）∈P（Ω）such that

Then there exists a constant Cp，p1independent of the functions f and g such that

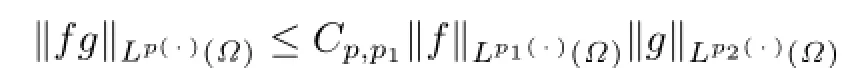
Then we have

Proof of Theorem 1.2Without loss of generality，we only consider the case m=2.For x∈Ω，0＜r＜R，denote

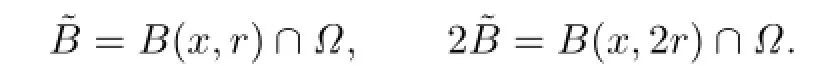
By the definition of the multilinear fractional integrals，we have

Applying the inequality（see［17］）

we obtain

If we denote

then

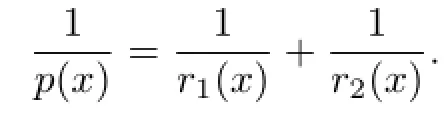
By using（2.1）and Lemma 2.3，we have

Now we consider the estimate of I1，

First we estimate D1.Since p1（·）∈LH0and p1（·）∈LH∞imply r1（·）∈LH0and r1（·）∈LH∞.By virtue of Lemma 2.4，we have

Next we estimate D2.We need the fact that if

then

By using Lemma 2.2，we obtain

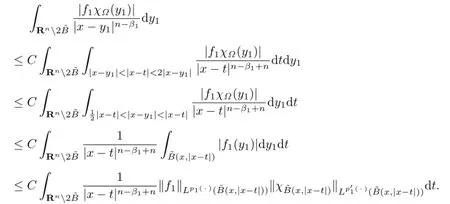
Since p1（·）∈LH0implies）∈LH0，by virtue of Lemma 2.1，we have∫

Since

by the upper two inequalities，we have∫

It follows that

Hence

By a similar arguments to that for I1we get that

Then we obtain

with the constant C independent of f1and f2.The proof of Theorem 1.2 is completed.

References

［1］Kenig C，Stein E M.Multilinear estimates and fractional integration.Math.Res.Lett.，1999，6：1-15.

［2］Grafakos L，Kalton N.Some remarks on multilinear maps and interpolation.Math.Ann.，2001，319：151-180.

［3］Moen K.Weighted inequalities for multilinear fractional integral operators.Collect.Math.，2009，60：213-238.

［4］Hu G，Lin C C.Weighted norm inequalities for multilinear singular integral operators and applications.arXiv：1208.6346［math.FA］.Submitted on 31 Aug.2012.

［5］Tao X，He S.The boundedness of multilinear operators on generalized Morrey spaces over the quasi-metric space of non-homogeneous type.J.Inequal.Appl.，2013，1：1-15.

［6］Iida T，Sato E，Sawano Y，Tanaka H.Multilinear fractional integrals on Morrey spaces.Acta Math.Sinica，2012，28：1375-1384.

［7］Tang L.Endpoint estimates for multilinear of fractional integrals.J.Aust.Math.Soc.，2008，84：419-429.

［8］Antontsev S，Shmarev S.Elliptic equations and systems with nonstandard growth conditions：existence，uniqueness and localization properties of solutions.Nonlinear Anal.，2006，65：728-761.

［9］Habermann J.Calder´on-Zygmund estimates for higher order systems with p（x）growth.Math. Z.，2008，258：427-462.

［10］Kov´aˇcik O，R´akosn´ık J.On spaces Lp（x）and Wk，p（x）.Czechoslovak Math.J.，1991，41：592-618.

［11］Kokilashvili V，Meskhi A.Boundedness of maxmial and singular operators in Morrey spaces with variable exponent.Armenian J.Math.，2008，1：18-28.

［12］Almeida A，Hasanov J，Samko S.Maximal and potential operators in variable exponent Morrey spaces.Georgian Math.J.，2008，15：195-208.

［13］Ho K-P.The fractional integral operators on Morrey spaces with variable exponent on unbounded domains.Math.Inequal.Appl.，2013，16：363-373.

［14］Tao X X，Yu X，Zhang H H.Multilinear Calder´on Zygmund operators on variable exponent Morrey spaces over domains.Appl.Math.J.Chinese Univ.，2011，26：187-197.

［15］Huang A W，Xu J S.Multilinear singular integrals and commutators in variable exponent Lebesgue spaces.Appl.Math.J.Chinese Univ.，2010，25：69-77.

［16］Capone C，Cruz-Uribe D，S F O，Fiorenza A.The fractional maximal operator and fractional integrals on variable Lpspaces.Rev.Mat.Iberoamericana，2007，23（3）：743-770.

［17］Izuki M.Herz and Amalgam spaces with variable exponent，the Haar wavelets and greediness of the wavelet system.East J.Approx.，2009，15：87-109.

10.13447/j.1674-5647.2015.03.07

date：Oct.16，2013.

The NSF（11201003）of China and the Education Committee（KJ2012A133）of Anhui Province.

.

E-mail address：15155369968@163.com（Wang M），shulsh@mail.ahnu.edu.cn（Shu L S）.of a family of related multilinear fractional integrals.Moen［3］established some weighted inequalities for multilinear fractional integral operators.Hu and Lin［4］got weighted norm inequalities for multilinear singular integral operators and applications.Tao and He［5］proved the boundedness of multilinear operators on generalized Morrey spaces over the quasi-metric space of non-homogeneous type.Also，many results about multilinear fractional integrals on Morrey spaces have been studied，（see［6-7］）.Especially，Tang［7］presented the boundedness of multilinear fractional integral operators on Morrey spaces.One of his results is rewrited as the following theorem：