Global Dynamics of a Predator-prey Model

Huang Rui，Pan Qiang-YouanD Bao Lian-zhang

（1.School of Mathematical Sciences，South China Normal University，Guangzhou，510631）

（2.School of Mathematics，Jilin University，Changchun，130012）

Communicated by Wang Chun-peng

Global Dynamics of a Predator-prey Model

Huang Rui1，Pan Qiang-You1anD Bao Lian-zhang2，*

（1.School of Mathematical Sciences，South China Normal University，Guangzhou，510631）

（2.School of Mathematics，Jilin University，Changchun，130012）

Communicated by Wang Chun-peng

In this paper，we consider a predator-prey model.A sufficient condition is presented for the stability of the equilibrium，which is different from the one for the model with Hassell-Varley type functional response.Furthermore，by constructing a Lyapunov function，we prove that the positive equilibrium is asymptotically stable.

Allee effect，asymptotically stable，predator-prey model

2010 MR subject classification：34A34，34D20

Document code：A

Article ID：1674-5647（2015）03-0274-07

1　Introduction

The Allee effect describes a scenario in which populations at low numbers are affected by a positive relationship between the per capita population growth rate and density，which increases their likelihood of extinction.Odum and Allee［1］got an approach of the model with Allee effect of single

where g（x）denotes the density-dependent per capita growth rate.In（1.1），three basic scenarios may occur（see［2］）：

1.Unconditional extinction.If g is negative for all x，we say that the Allee effect is too strong.In this situation，populations go inevitably extinct regardless of their initial sizes；

2.Extinction-survival.If g is positive for intermediate value but negative for very low or high values of x.In this situation，two equilibria emerge.It is so-called the model with strong Allee effect；

3.Unconditional survival.By weakening the influence of the Allee effect，g is always positive.In this situation，the population can reach the carrying capacity.

With the strong Allee effect，the following growth model for one species was proposed in［3］

where a is the organic growth of the prey，S＞0 a critical population threshold，K＞S the carrying capacity of the prey in the absence of the predator.A general two-component predator-prey model is of the following form（see［4］）

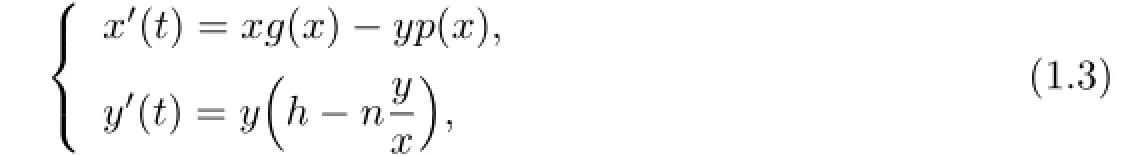
where x（t）and y（t）stand for the population densities of the prey and the predator at time t＞0 respectively，g（x）the per capita growth rate of the prey in the absence of the predator，p（x）the so-called predator functional response to the prey，h＞0 the intrinsic growth rates of the predator，n＞0 a measure of the food quality that the prey provides for conversion into predator birth.

Another predator-prey model with Hassell-Varley type functional response takes the following form（see［5］）

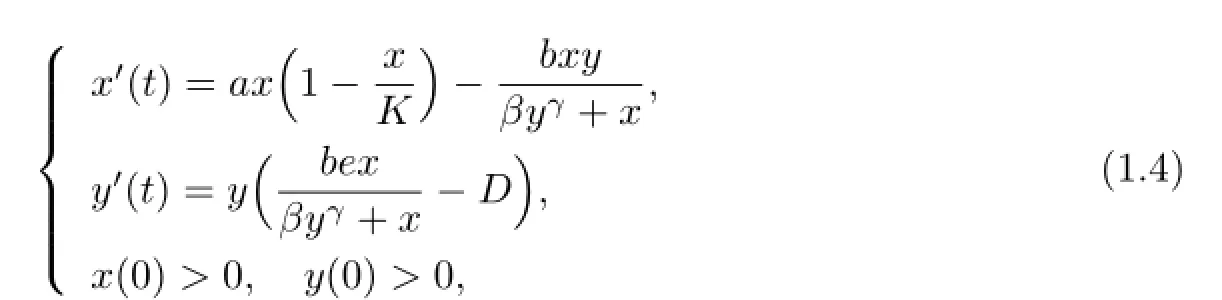
where γ is called the Hassell-Varley constant with γ∈（0，1），D＞0 the death rate of the predator，b＞0 the intrinsic growth rate of the predator，β＞0 the half saturation constant，e＞0 the conversion factor denoting the number of newly born predators for each captured prey.Later，Yu and Sunet al.［6］considered the following more general predator-prey model incorporating a constant prey refuge with Hassell-Varley type functional response

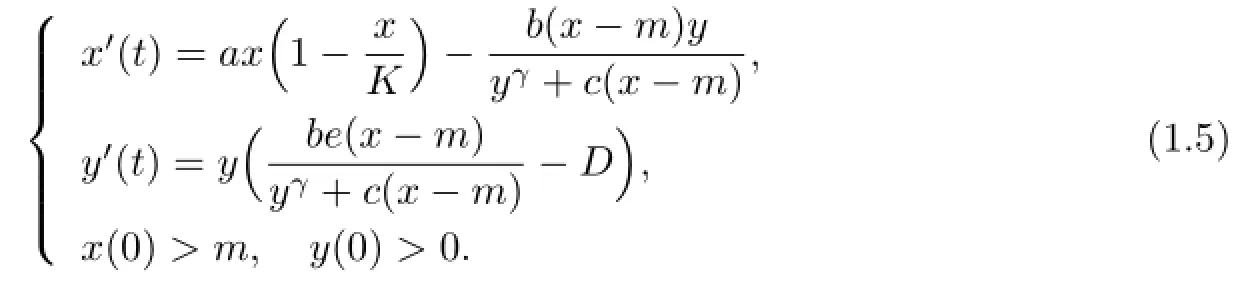
They proved that（1.5）admits a globally asymptotically stable equilibrium provided that

Inspired by（1.2）-（1.5），in this paper，we consider the following predator-prey model with strong Allee effect：

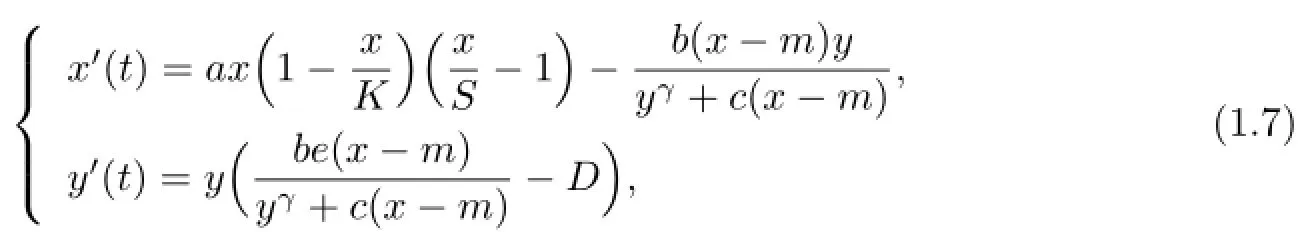
where m＞0 is a constant denoting the number of the prey using refuges，which protects m of the prey from the predation，c＞0 is a constant.In this paper，we show that undersome condition，the equilibrium of the predator-prey model（1.7）is globally asymptotically stable.

We define

Theorem 1.1If be＞Dc，m∗≤m＜K and γ∗＜γ＜1，then（1.7）admits a globally asymptotically stable equilibrium.

Remark 1.2The assumption be＞Dc means that the predator death rate D can not be too large，which is a natural condition.

Since 0＜d＜1，by（1.6），a simple calculation shows that the lower bound of refuge constant m for（1.5）is less than.While，at least for the case of K＜2S，the lower bound of refuge constant m for（1.7）with strong Allee effect is bigger thanThat means，if the strong Allee effect is taken into account，then the refuge constant should be more big in some sense.That is to say，the species with strong Allee effect is easier to die out than the Hassell-Varley one，so the number of the prey using refuges could not be too small.Actually，it is also shown in［7］that a species growing with the strong Allee effect at a low population is difficult to survive.

2　Proof of the Main Result

In this section，we give the proof of Theorem 1.1.Since x and y stand for the population densities，in this paper，we consider（1.7）in Ω=｛（x，y）：x≥0，y≥0｝.By the scalings，and we still denoteby t，x，y，respectively，in the final，then（1.7）turns to

Combining the above two equations together，we have

By the above equation，we are informed that there are only four cases for x∗and y∗：

Since（x∗，y∗）∈Ω，Cases 1，2 and 4 should be ruled out directly，and only Case 3 is accepted.Furthermore，by the assumption be＞Dc，we have 0＜d＜1.Then by（2.2）and the positivity of y∗，we have

The variational matrix of（2.1）is

A（x，y）

A simple calculation shows that

At E2，we have

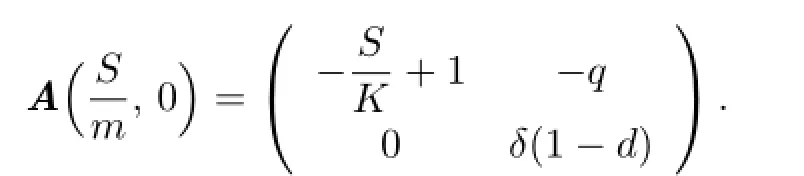
Obviously，we have the following propositions.

Proposition 2.1For（2.1），the following statements hold：

（1）E0and E1are saddle points，E2is an unstable point；

（2）if detA（x∗，y∗）＞ 0 and trA（x∗，y∗）＜ 0，then E∗is asymptotically stable；if detA（x∗，y∗）＞0 and trA（x∗，y∗）＞0，then E∗is unstable；

（3）if detA（x∗，y∗）＜0，then E∗is a saddle point.

Proposition 2.2Under the assumptions of Theorem 1.1，（2.1）admits an asymptotically stable equilibrium.

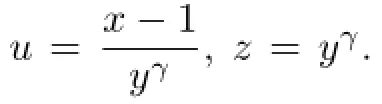
where

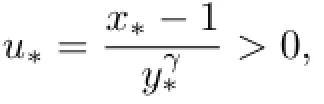
We have

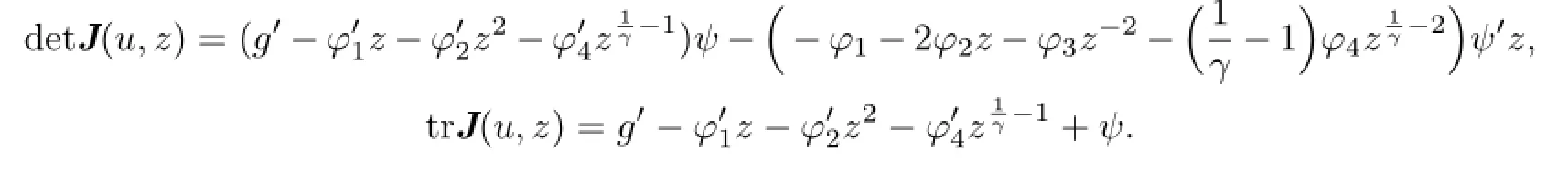
It follows from g1（u∗，z∗）=0 and z∗＞0 that ψ（u∗）=0.Then

By f1（u∗，z∗）=0，we have

By（2.5），（2.7）and Proposition 2.1，we have that e∗=（u∗，z∗）is asymptotically stable.The proof of this proposition is complete.

Since both the transformations from（1.7）to（2.1）and from（2.1）to（2.4）are reversible，we are informed from the above proposition that（1.7）admits an asymptotically stable equilibrium.By the same reason，to prove Theorem 1.1，we only need to consider（2.4）.

Proof of Theorem 1.1Consider the following Lyapunov function

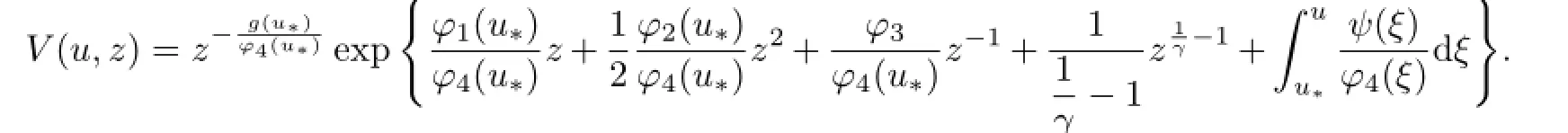
The derivative of V along the solution of system（2.4）is

Since

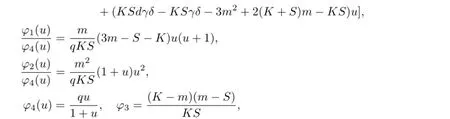
When u＞u∗，we have

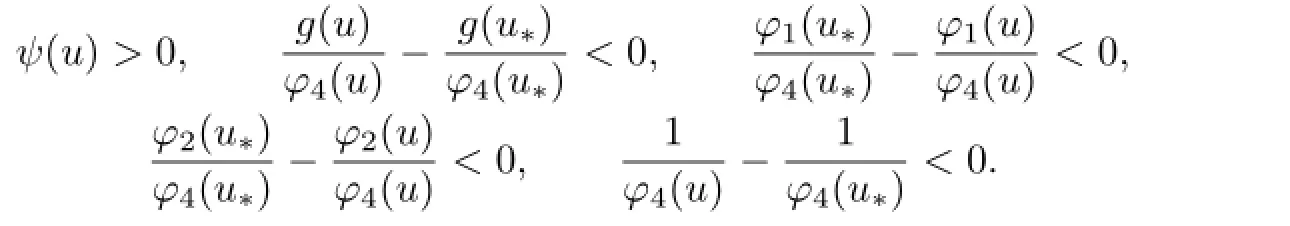
References

［1］Odum H T，Allee W C.A note on the stable point of populations showing both intraspecific cooperation and disoperation.Ecology，1954，35：95-97.

［2］Boukal D S，Berec L.Single-species models of the Allee effect：extinction boundaries，sex ratios and mate encounters.J.Theoret.Biol.，2002，218：375-394.

［3］Gruntfest Y，Ariditi R，Dombrovsky Y.A fragmented population in a varying environment.J. Theoret.Biol.，1997，185：539-547.

［4］Pallav J P，Prashanata K M.Bifurcation analysis of a modified Leslie-Gower predator-prey model with Beddington-DeAngelis functional response and strong Allee effect.Math.Comput. Simulation，2014，97：123-146.

［5］Hsu S B，Hwang T W，Kuang Y.Global analysis of a predator-prey model with Hassell-Varley type function response.Discrete Contin.Dyn.Syst.Ser.B，2008，10：857-871.

［6］Yu X，Sun F.Global dynamics of a predator-prey model incorporating a constant prey refuge. Electronic J.Differential Equations，2013，4：1-8.

［7］Courchamp F，Clutton-Brock T，Grenfell B.Inverse density dependence and the Allee effect. Trends in Ecology and Evolution，1999，14：405-410.

10.13447/j.1674-5647.2015.03.10

date：Feb.1，2015.

The NSF（11071099）of China.

.

E-mail address：huangrui@m.scnu.edu.cn（Huang R），lzbao@jlu.edu.cn（Bao L Z）.