A Note on Weighted Composition Operators on the Fock Space

Feng Li-xia anD Zhao Lian-kuo

（School of Mathematics and Computer Science，Shanxi Normal University，Linfen，Shanxi，041004）

Communicated by Ji You-qing

A Note on Weighted Composition Operators on the Fock Space

Feng Li-xia anD Zhao Lian-kuo*

（School of Mathematics and Computer Science，Shanxi Normal University，Linfen，Shanxi，041004）

Communicated by Ji You-qing

Based on a new characterization of bounded and compact weighted composition operators on the Fock space obtained by Le T（Le T.Normal and isometric weighted composition operators on the Fock space.Bull.London.Math.Soc.，2014，46：847-856），this paper shows that a bounded weighted composition operator on the Fock space is a Fredholm operator if and only if it is an invertible operator，and if and only if it is a nonzero constant multiple of a unitary operator.The result is very different from the corresponding results on the Hardy space and the Bergman space.

Fock space，weighted composition operator，Fredholm，invertible，unitary

2010 MR subject classification：47B32

Document code：A

Article ID：1674-5647（2015）03-0281-04

1　Introduction

Recently，weighted composition operators on the Fock space have been studied in［1-8］.In［3］，the boundedness and compactness of weighted composition operators on the Fock space are characterized explicitly，as corollaries，the normal and isometric weighted composition operators are characterized completely.The self-adjoint and unitary weighted composition operators and their spectrum on the Fock space are characterized in［7-8］，respectively.In this paper，we study Fredholm weighted composition operators on the Fock space.It is amazing that a bounded weighted composition operator on the Fock space is a Fredholm operator if and only if it is an invertible operator，and if and only if it is a nonzero constantmultiple of a unitary operator.

Recall that the Fock space F2is the space of entire functions f on C satisfying

where dm is the usual Lebesgue measure on C.It is well known that F2is a reproducing kernel Hilbert space with reproducing kernel function

Let kwbe the normalization of Kw.Then

For more information on the Fock spaces and their operators，see［9］.

For an entire function φ on C and ψ∈F2，the weighted composition operator Cψ，φon F2is defined as

Our main result is as follows.

Theorem 1.1Let φ be an entire function on C and ψ be a nonzero function in F2.If Cψ，φis bounded on F2，then the following conditions are equivalent：

（1）Cψ，φis a nonzero constant multiple of a unitary operator；

（2）Cψ，φis an invertible operator；

（3）Cψ，φis a Fredholm operator.

2　Proof of the Main Result

Before proving Theorem 1.1，some known results are needed.

Lemma 2.1Let φ be an entire function on C and ψ∈F2.If Cψ，φis bounded on F2，then

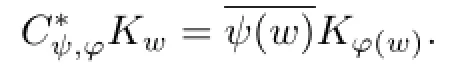
Lemma 2.2［3］Let φ be an entire function on C and ψ be a nonzero function in F2.

（1）Cψ，φis bounded on F2if and only if φ（z）=az+b with|a|≤1 and

（2）Cψ，φis compact on F2if and only if φ（z）=az+b with|a|＜1 and

The following result follows from Propositions 2.1，3.1 and Theorem 2.2 in［3］.

Lemma 2.3Let φ（z）=az+b with|a|=1 and ψ be a nonzero function in F2.If Cψ，φis bounded on F2，then Cψ，φis a nonzero constant multiple of a unitary operator.

Now we give the proof of Theorem 1.1.

Proof of Theorem 1.1Obviously，it suffices to prove that the condition（3）implies the condition（1）.

Since Cψ，φis bounded on F2，by Lemma 2.2，we assume that

By Lemma 2.3，when|a|=1，the conclusion holds.In the following，we prove that the case|a|＜1 does not occur.

If Cψ，φis a Fredholm operator，then there exist a bounded operator A and a compact operator B on F2such that

where I is the identity operator.

By Lemma 2.1，

we have

Since B is compact and kwweakly converges to 0 as|w|→∞，one has

It follows that there exists a positive constant r such that

By（2.2），we have

which implies that ψ has no zeroes in｛w∈C，|w|＞r｝.

Let a1，a2，···，anbe the zeroes of ψ.Then

for some entire function f with f is zero-free in C.

By（2.1），（2.3）and（2.4），we have

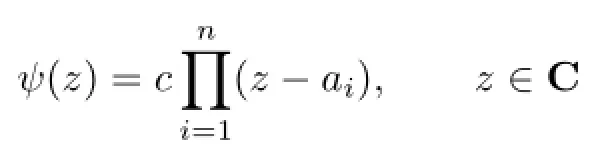
for some constant c.

which implies that Cψ，φis compact by Lemma 2.2（2），a contradiction.

References

［1］Carswell B J，MacCluer B D，Schuster A.Compostion operators on the Fock space.Acta Sci. Math.（Szeged），2003，69：871-887.

［2］Guo K Y，Izuchi K.Composition operators on Fock type spaces，Acta Sci.Math.（Szeged），2008，74：805-826.

［3］Le T.Normal and isometric weighted composition operators on the Fock space.Bull.London. Math.Soc.，2014，46：847-856.

［4］Stevi´c S.Weighted composition operators between Fock-type spaces in Cn.Appl.Math.Comput.，2009，215：2750-2760.

［5］Ueki S.Weighted composition operator on the Fock space.Proc.Amer.Math.Soc.，2007，135（5）：1405-1410.

［6］Ueki S.Weighted composition operator on some function space of entire functions.Bull.Belg. Math.Soc.Simon Stevin，2010，17（2）：343-353.

［7］Zhao L，Pang C.A class of weighted composition operaors on the Fock space.J.Math.Res. Appl.，to appear.

［8］Zhao L.Unitary weighted composition operaors on Fock space of Cn.Complex Anal.Oper. Theory，2014，8：581-590.

［9］Zhu K H.Analysis of Fock Space.New York：Springer，2012.

10.13447/j.1674-5647.2015.03.11

date：Dec.25，2014.

The NSF（11201274 and 11471189）of China.

.

E-mail address：lixialx@sina.com（Feng L X），liankuozhao@sina.com（Zhao L K）.