Exact Controllability for a Class of Nonlinear Evolution Control Systems

L¨u Yue

（College of Mathematics，Jilin University，Changchun，130012）

Communicated by Li Yong

Exact Controllability for a Class of Nonlinear Evolution Control Systems

L¨u Yue

（College of Mathematics，Jilin University，Changchun，130012）

Communicated by Li Yong

In this paper，we study the exact controllability of the nonlinear control systems.The controllability results by using the monotone operator theory are established.No compactness assumptions are imposed in the main results.

controllability，monotone operator，nonlinear evolution system，coercivity condition

2010 MR subject classification：35J30，35J35

Document code：A

Article ID：1674-5647（2015）03-0285-04

1　Introduction

In this paper，we study the exact controllability of the following nonlinear systems：{

where J=［0，T］，the state of the system x∈X and u（t）∈V is the control at time t，X and V are Hilbert spaces.Let Y=L2（0，T；X）be the solution space and U=L2（0，T；V）be the control function space.The nonlinear function f：J×X×V→X，A（t）is a linear operator on X for each t，B（t）：V→X is a bounded linear operator.

We know that the linear system

can be applied to many fields such as engineering，economic growth model，continuous mechanics and so on.Many properties and classical results have been obtained based on researching the linear system.However，the nonlinear systems（1.1）are more common in practical problems.Naturally，people want to know：if a controllable linear system isperturbed by a nonlinear perturbation f（t，x，u）and becomes a nonlinear system

then will the perturbed system preserve the controllability of the linear system？In 1972，Mirza and Womack［1］considered the nonlinear system above and obtained controllability.In the same year，Lukes［2］proved the controllability of this nonlinear system with A，B constant matrices.In 1976，Dauer［3］concluded that the system was completely controllable.Recently，many authors have studied the controllability to this system in infinite dimensional space（see［4-11］）.In this paper，we present some abstract results for nonlinear control system with some useful corollaries.

The outlay of the paper is as follow.In Section 2，we give some preliminaries.We study the system（1.1）and obtain the controllability for this system in Section 3.

2　Preliminaries

Firstly，we introduce some notations，definitions and a lemma，which are used in this paper.

For（1.1），we suppose that A（t）generates an evolution system｛E（t，s）｝，f：J×X×V→X is a nonlinear operator，measurable in the first argument and continuous in the last two arguments.C（J，X）denotes the set of all continuous functions x from J to X with the usual maximum norm denoted by‖·‖C.

Definition 2.1A function x∈C（J，X）is called a mild solution of（1.1）on J if

Definition 2.2The system（1.1）is said to be controllable on the interval J=［0，T］if for every x1∈X，there exists a control u∈U such that the mild solution x（t）of（1.1）satisfies x（0）=0 and x（T）=x1.

X is a Hilbert space with scalar product〈·，·〉.An operator F：X → X is called strongly monotone（or monotone）if there exists β＞0（or β=0）such that

F is called hemicontinuous if x∈X，h∈X，t＞0，and if t→0 implies F（x+th）⇀F（x），here“⇀”means weak convergence in X.

Lemma 2.1［12］Suppose that T：X→X is maximal monotone and θ∈D（T），P：X→X is hemicontinuous，monotone，bounded and satisfies coercive condition，i.e.，

Then T+P is onto.

3　Main Result

We reduce the controllability problem to a solvability problem.Define the following operator：

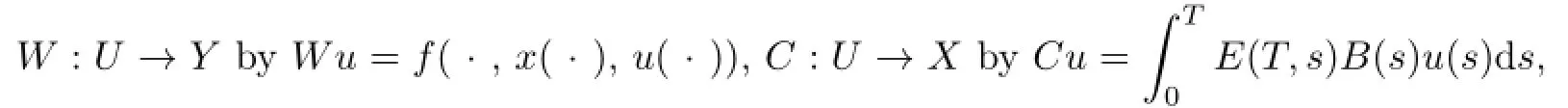
where x（·）is the solution of（1.1）corresponding to u∈U.Clearly，the operator C is bounded and linear.

We call the system

is the corresponding linear system of（1.1）.

Definition 3.1We call a bounded linear operator S：X→U a steering operator if S steers the linear system（3.1）from 0 to x1（x1∈X）.

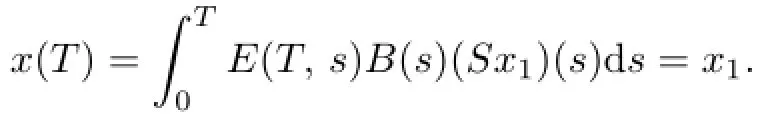
In fact，if u=Sx1（x1∈X），then

Clearly，CS=I，the identity operator on X.Thus，if there exists a steering operator S，then u=Sx1acts as a control and the linear system is controllable.For the steering operator we have the following results.

Lemma 3.1［13］The linear system（3.1）is exactly controllable if and only if there exists a steering operator.

We now assume the controllability of the linear system and proceed to prove the exact controllability of the nonlinear system.

That is，x1=Fu+Cu.Applying S on both sides，we get u0=SFu+u，where u0is the control，steering the linear system from 0 to x1.

Thus，the problem of controllability reduces to solvability problem of the operator equation

Theorem 3.1Assume that the linear operator C and the operator F are monotone，and F is coercive.Then the equation（3.2）is solvable in U.

Proof.The equation（3.2）can be written as SFu=u0-u，that is，Fu∈S-1（u0-u），so，if

then the equation（3.2）is solvable.

Let z=u-u0（u0∈U is given）.Then the equation（3.3）can be written as θ∈（F1+T）z，where

Clearly，F1is monotone and coercive，and by the character of f，we know F1is continuous and bounded.C is continuous and monotone.So C is maximal monotone.Then S-1is maximal monotone by S is linear and

Thus T is maximal monotone.Since Sθ=θ，we have θ∈D（T）.By Lemma 2.1，F1+T is onto.Then the equation（3.3）is solvable.So the equation（3.2）is solvable in U.This completes the proof.

Thus we can obtain the following result.

Theorem 3.2Assume that the linear system is exactly controllable with a steering operator S，and the conditions of Theorem 3.1 are all satisfied.Then the nonlinear system（1.1）is controllable on J.

References

［1］Mirza K，Womack B F.On the controllability of a class of nonlinear systems.IEEE Trans.，1972，17：531-535.

［2］Lukes D L.Global controllability of nonlinear systems.SIAM J.Control，1972，10：112-126.

［3］Dauer J P.Nonlinear perturbations of quasi-linear control systems.J.Math.Anal.Appl.，1976，37：717-725.

［4］Natio K.Controllability of semilinear control systems dominated by the linear part.SIAM J. Control Optim.，1987，25：715-722.

［5］Lasiecka L，Triggiani R.Exact controllabilty of semilinear abstract systems with application to waves and plates boundary control problems.Appl.Math.Optim.，1991，23：109-154.

［6］Quinn M D，Carmichael N.An approach to nonlinear control problems using fixed point methods degree theory and pseudo-inverses.Numer.Funct.Anal.Optim.，1984-1985，7：197-219.

［7］Chukwu E N，Lenhart S M.Controllability question for nonlinear systems in astract spaces. J.Optim.Theory Appl.，1991，68：437-462.

［8］Do V N.A note on approximate controllability of semilinear systems.Systems Control Lett.，1989，12：365-371.

［9］Zhou H X.Approximate controllability for a class of semilinear abstract equations.SIAM J. Control.Optim.，1983，21：551-565.

［10］Bain W.Approximate controllability for semilinear systems.Acta Math.Hungar.，1998，81：41-57.

［11］Zhang X.Exact controllability of semilinear evolution systems and application.J.Optim. Theory Appl.，2000，107：415-453.

［12］Deimling K.Nonlinear Function Analysis.Berlin：Springer-Verlag，1980.

［13］Chalishajar Dimplekumar N，George Raju K.Exact controllability of generalized Hammerstein type integral equation and applications.Electron.J.Differential Equations，2006，142：1-15.

10.13447/j.1674-5647.2015.03.12

date：April 17，2015.

E-mail address：lvyue@jlu.edu.cn（L¨u Y）.