基于高精度非圆二次曲线零件加工策略研究
苟建峰,彭美武,杨保成
(1.四川大学制造科学与工程学院,成都 610065;2.四川工程职业技术学院机电工程系,四川德阳 618000)
基于高精度非圆二次曲线零件加工策略研究
苟建峰1,2,彭美武2,杨保成2
(1.四川大学制造科学与工程学院,成都 610065;2.四川工程职业技术学院机电工程系,四川德阳 618000)
文章针对数控车削中高精度非圆二次曲线零件轮廓复杂,编程困难(往往采用参数编程),且加工要求和精度高。而参数变量的选择和赋值往往由编程人员直接凭经验选取,加工要求和精度很难保证。因此在分析对比二次曲线拟合方法后选择最优的拟合方法,同时根据加工的技术要求和精度,合理选择参数,并通过数学推导计算出最佳的参数赋值。以具体实例,完成非圆二次曲线零件的参数编程。通过验证,该方法极大的提高了加工精度,节省了加工时间。在实际生产中有一定的推广应用价值。
高精度;二次曲线;加工策略
0 引言
随着数控技术的发展,在机械制造业中,二次曲线类零件比比皆是,其编程加工比较困难。以往对这类二次曲线轮廓加工一般采用参数编程。而参数变量的选择和赋值往往由编程人员直接凭经验选取,加工要求和精度很难保证。
本文针对上述问题在分析对比非圆二次曲线拟合方法后选择最优的拟合方法,同时根据加工的技术要求和精度,合理选择参数,并通过数学推导计算出最佳的参数赋值。并结合具体零件如图1所示,毛坯为φ40mm×90mm的棒料,材料45钢,小批量生产,通过在数控车床上加工验证,该方法极大的提高了加工精度,节省了加工时间。也为其他二次曲线的参数编程提供参考,在实际生产中有一定的推广应用价值。
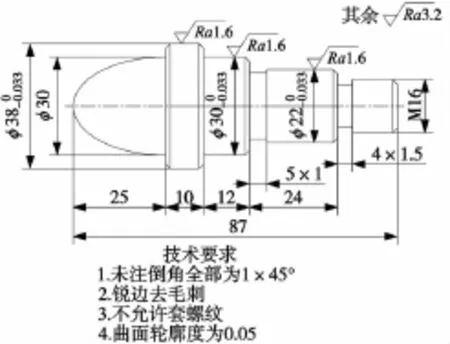
图1 二次曲线零件图
1 二次曲线插补处理及算法
1.1 插补处理
针对非圆二次曲线编程时没有现成的指令可用,往往需要进行插补处理。所谓插补就是按一定的算法,将连续的二次曲线分割成若干个微小的线段,以直线或圆弧代替每段微小的线段去逼近轮廓曲线以此代替原有的二次曲线,即“数据点的密化”。当然,数据点越多,拟合出的曲线越光滑,轮廓曲线精度就越高。但程序也就越复杂,加工效率就越低,所以,数据点密化要适当。
1.2 常用拟合算法
对二次曲线的拟合方法,常用的有等间距直线逼近法、等弦长直线逼近法、等误差直线逼近法和圆弧逼近法等,如图2所示。
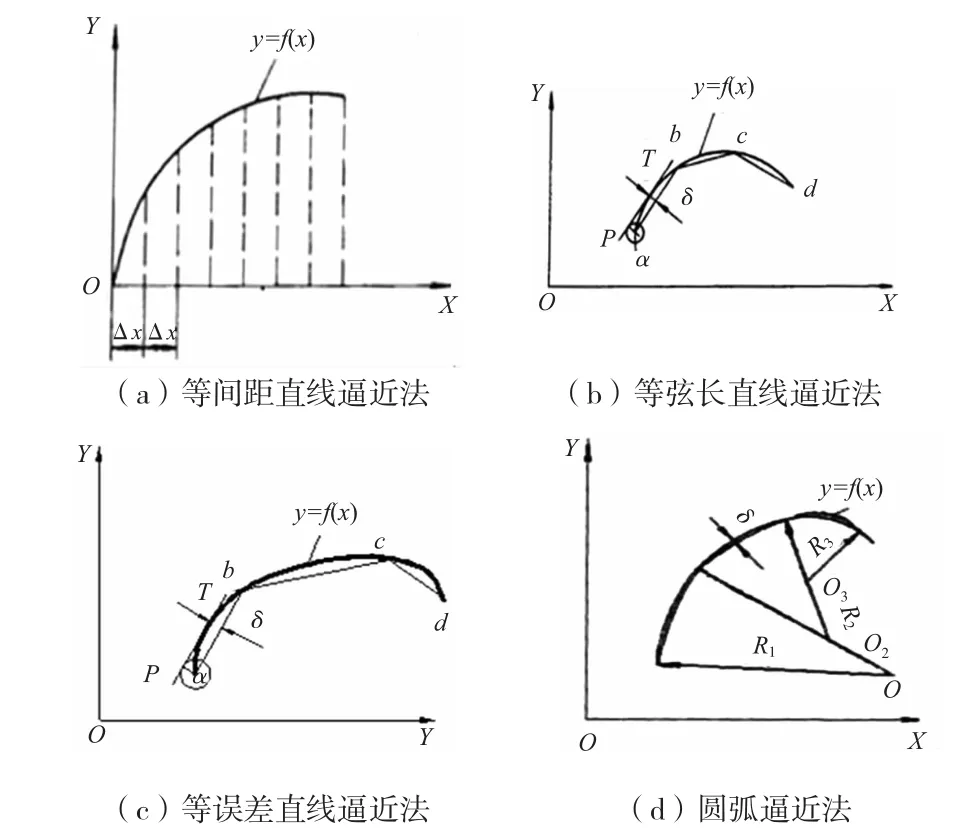
图2 四种拟合方法
(1)等间距直线逼近法
等间距法是将其中一坐标轴以相等的间距进行划分,计算出节点坐标后,用直线再去逼近二次曲线。该方法最简单,但拟合精度与间距大小密切相关,间距越大精度越低,而且步长及加工精度分布不均。一般如果用参数方程计算变量时,该方法可以转化成等角度直线逼近法。此时节点分布均匀,所以在同等条件下优选等角度直线逼近法。
(2)等弦长直线逼近法
等弦长直线逼近法是用长度相等的直线段去逼近曲线。等弦长法和等间距法都属于直线拟合法,计算简单。但当曲线的曲率较大时,因步长、间距为定值,会使节点增加,程序段数随之也增多。当曲率变化较大时,零件表面粗糙度也随之变化较大,影响加工质量。
(3)等误差直线逼近法
等误差直线逼近法是指各逼近直线与目标曲线间的误差δ均相等,但步长和间距不为定值。该法节点相对较少,程序简单,加工精度较高,但节点计算复杂,手工求解比较困难。
(4)圆弧逼近法
圆弧逼近法是用圆弧去逼近曲线。该方法节点数少,程序简单,拟合表面光滑,精度较高。但与其上述直线拟合方法相比计算比较繁琐。
根据该零件的加工要求和精度,并且通过结合以上插补方法的对比和分析,可知等角度直线法计算简便,误差分布均匀,且节点数少,程序运行效率较高,所以我们选择等角度直线法加工。
2 参数变量的选择及赋值的确定
2.1 参数变量的确定
首先根据待加工零件的二次曲线轮廓特征分析,建立曲线相应的数学模型表达式。
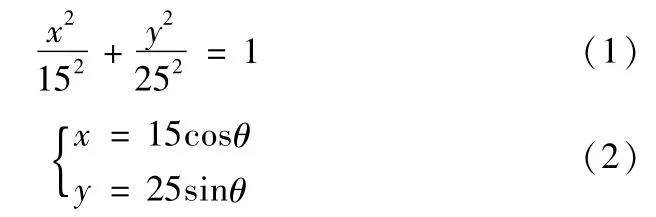
一般曲线的数学表达式往往有以上两种。为了编程方便,往往采用二次曲线的参数方程,同时需要根据工件坐标系做适当的参数变换,选择合适的自变量,来表示二次曲线上各关链点的坐标表达式。此零件利用二次曲线的参数方程表达式,以θ参数作为自变量,X和Z作为参数的函数。
2.2 最大步距角的确定
当采用等角度法逼近曲线时,即要保证加工精度同时还要减少节点数,就必须计算最大步距角。而逼近误差在曲率半径最小处最大,只要最大逼近误差小于允许误差,那么就能满足加工精度要求,因此必须求出曲率半径最小处的最大步距角。
由高等数学知识可知曲线的曲率公式为:
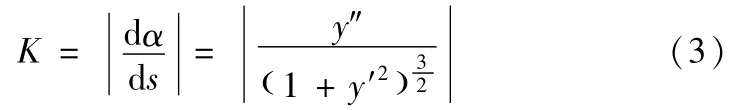
其中y=f(x)为曲线,d s为曲线弧长微分,α为曲线上点的切线倾角,k为曲率,曲率半径
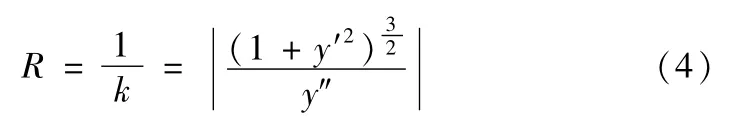
最小曲率半径Rmin往往通过曲率半径求导计算X值,再代入式4中便可求出。
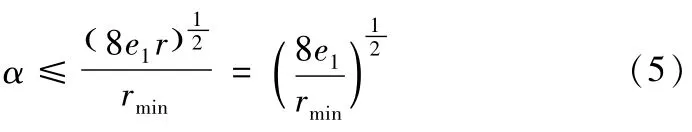
其中角度步距角为α,步距为λ,曲率半径为r。
由于该零件的加工要求和精度可计算得,曲面公差0.05mm,所以取允δ=0.01。
将式(2)进行求导代入(4)式可得:
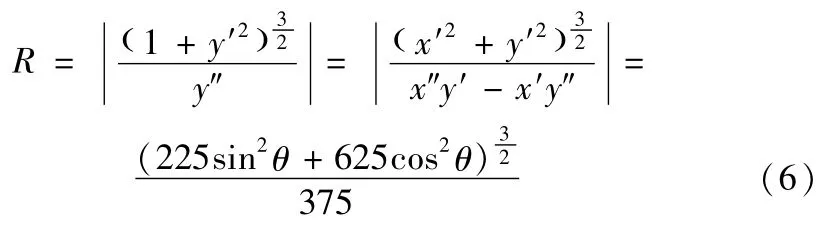
R最小即100sin2θ+169cos2θ最小。通过对其求导得:
所以,取角度增加量α=0.3即可满足要求。
3 宏程序开发与实施
完成该非圆二次曲线零件最优的拟合方法的确定,以及确定合适的参数并根据加工的技术要求和精度,准确计算出最佳的参数赋值后。利用宏程序分别使用一个循环进行粗精加工。流程如图4所示。选用FANUC0i系统进行编程,宏程序如下:
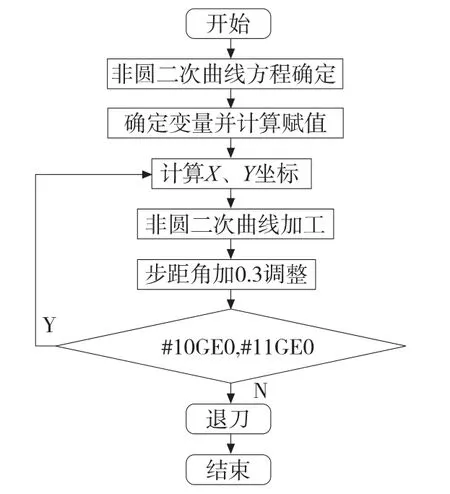
图4 宏程序开发流程图


4 加工验证
完成上述零件的程序编制后,首先选用CK3050机床,其系统为FANUC 0i系统。93°外圆车刀,转速1500r/min,进给速度0.15mm/r,进行实际加工,完全达到零件的要求。与此同时,为了验证效果,我们又分别选取0.1和1两种不同的步距角,所有参数设置均完全相同。虽然宏程序几乎没有变动,只是步距角的赋值发生变化而已。结果三种程序加工零件的质量差别悬殊,三种不同赋值的步距角的宏程序加工对比如表1所示。因此选择最优的拟合方法,同时合理选择参数,并精确确定最佳的参数赋值。对二次曲线零件的加工要求和精度保证非常可取。
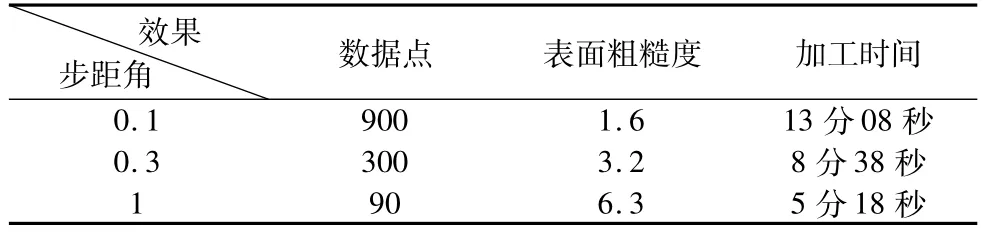
表1 三种不同赋值的步距角的程序比较
5 结束语
非圆二次曲线种类繁多。本文具体以椭圆为例。研究提出了结合具体非圆二次曲线分析对比其拟合方法后选择最优的拟合方法,同时根据加工的技术要求和精度,合理选择参数,并通过数学推导计算出最佳的参数赋值。解决了以往参数变量的选择和赋值由编程人员直接凭经验选取,加工要求和精度很难保证的难题。通过验证,该方法极大的提高了加工精度,节省了加工时间。也为其他二次曲线的参数编程提供参考,在实际生产中有一定的推广应用价值。
[1]徐巍,王宇晗.FANUC和SIEMENS的宏程序处理非圆曲线的编译实例[J].组合机床与自动化加工技术,2008(9):72-74.[2]薛明赵薇.基于数控车削非圆二次曲线零件加工的研究[J].组合机床与自动化加工技术,2013(4):129-131.
[3]吴胜强.宏程序在非圆曲线轮廓加工中的应用[J].机床与液压,2009,37(4):189-190.
[4]斯密德.FANUC数控系统用户宏程序与编程技巧[M].北京:化学工业出版社,2007.
[5]陈洪涛.数控加工工艺与编程[M].北京:高等教育出版社,2003.
[6]杨静云,石玉宝.数控编程与工艺对椭圆曲面加工精度的影响[J].制造业自动化,2010,33(12):95-96.
[7]王峰波,孙士彬.FANUC系统宏程序在抛物线类零件中的应用[J].煤矿机械,2011,32(10):148-150.
[8]关颖.基于FANUC系统的双曲线宏程序编制与加工解析[J].机床与液压,2012,40(8):59-60,90.
[9]彭美武,杨顺田.计算机数控技术[M].北京:化学工业出版社,2011.
[10]袁永富,熊福林,王甫茂,等.椭圆曲线轮廓加工的逼近精度分析[J].煤矿机械,2011,32(6):142-144.
Based on High Precision Non-circular Quadratic Curve Parts Processing Strategy Research
GOU Jian-feng1,2,PENG Mei-wu2,YANG Bao-cheng2
(1.College of Manufacturing Science and Engineering,Sichuan University,Chengdu 610065,China;2.Department of Mechanical and Electrical Engineering,Sichuan Engineering Technical College,Deyang Sichuan 618000,China)
In this paper,the numerical control turning conic parts in complex contour,programming difficulty,often using parameter programming.Variables and parameters selection and assignment is often directly by the programmers with experience selection,processing requirements and the precision is difficult to guarantee.Therefore quadratic curve fitting based on the analysis of contrast methods to choose the optimal fitting method,according to the requirements of the processing technology and precision at the same time,choose the parameter,and through the mathematic model to calculate the optimum parameters of the assignment.With specific examples,to complete the parameters of the conic parts programming.Through the verification,the method greatly improves the machining accuracy,but also save the processing time.In the actual production has a certain application value.
high precision;conic;processing strategies
TH165;TG51
A
1001-2265(2015)06-0146-03 DOI:10.13462/j.cnki.mmtamt.2015.06.040
2014-09-25;
2014-10-23
苟建峰(1983—),男,陕西宝鸡人,四川工程职业技术学院讲师,硕士,研究方向为数控加工技术,(E-mail)gjf0423@163.com。

