双臂移动机器人机械臂的协调工作空间分析*

田海波，尚万峰，马宏伟

（西安科技大学机械工程学院，西安 710054）

双臂移动机器人机械臂的协调工作空间分析*

田海波，尚万峰，马宏伟

（西安科技大学机械工程学院，西安 710054）

双臂机器人机械臂的协调工作区间是指左臂和右臂工作空间的重叠区域形成的工作区，可用来表征这种机器人运动灵活性。给出双臂机器人的主要结构，经过简化得到其运动学模型，求出末端作用点的位置向量。结合蒙特卡洛法和网格划分法，提出一种新的方法，研究该机器人机械臂的工作空间问题，得到了两机械臂独立工作时的工作空间点云图和协调工作空间点云图。结果表明，在基座关节可以转动的情况下，协调工作空间能够实现对机器人的全周覆盖，可以满足使用要求。

双臂机器人；机械臂；工作空间；蒙特卡洛法

0 引言

目前，单臂机器人在工业制造领域和特种作业领域应用非常广泛［1-3］，但面对许多复杂任务时，单臂操作就无能为力。近年来双臂服务机器人的研究和应用得到了快速发展，这种机器人两臂之间相互通信，协作配合，能完成很多单臂机器人无法完成的任务。从研究角度看，双臂机器人可以看作两个单臂机器人在一起工作，可以参考单臂机器人的成果对其进行研究［4］。

工作空间是指机器人机械臂的末端作用点能够到达的空间位置集。对于双臂机器人而言，它由左臂工作空间和右臂工作空间组成，二者之间存在的重叠区域，称为协调工作区，是用来表征这种机器人运动灵活性的主要指标［5］。

迄今为止，机器人工作空间的求解方法主要有图解法、解析法和数值法三大类。图解法的特点是比较直观，少自由度机器人的空间剖截面或剖截线可以直接求得，但对多自由度机器人就难有作为［6］。解析法是用数学包络法把工作空间的边界用解析式表示出来，但过程繁琐，不适合关节数多于3的机器人［7］。数值法则是给机械臂各关节转角或位移选取尽可能多的独立的值，再建立机器人的运动学模型，由此得到末端作用点的坐标，这些坐标点的集合就构成了机器人的工作空间［8］。仿真法也是一种数值法，它是利用某些工程软件建立机器人的运动模型，不需运动学运算，可以直接仿真。其缺点是计算过程完全取决于软件，不便分析［9］。数值法避免了复杂的计算过程，操作相对简单，适用于任意机构，虽然计算量大，但随着计算机软硬件的不断更新，这已经不再成为障碍。

本文研究了一种典型双臂机器人的结构，对其进行了运动学分析，将数值法和网格划分法［10］结合，求出了其单臂工作空间和协调工作空间的形状，为此机器人进一步的研究打下基础。

1 双臂机器人结构

文中研究的一种双臂机器人，由行驶平台、基座关节和左右两侧各一个机械臂组成，如图1所示。两个机械臂结构相同，都包括肩关节、肘关节、横摆关节和末端回转关节。机械手所处的空间位置由肩关节、肘关节和横摆关节确定，而机械手的姿态则由末端回转关节决定。

图1 双臂机器人的主要构成

该机器人的抓取作业过程如下：首先驱动履带行驶到目标位置，接着转动基座关节，摆好姿态。随后在控制器的指令下，肩关节、肘关节、横摆关节和末端回转关节一起动作，两只机械手同时伸向目标位置，抓取目标。这个过程可以看作两个单臂机器人在同时动作，不同的是，其双臂必须协调工作，才能充分发挥它的优势，因此必须放在一起分析。

2 双臂机器人运动学分析

运动学分析是研究机器人工作空间的基础。要分析双臂机器人的工作空间，首先必须根据关节结构，考虑各种约束，分别对两个机械臂进行运动学分析。

2.1 运动模型简化

选择D2H方法来设定双臂机器人的坐标系，这样可以更好地描述各杆件的结构参数和相互间的运动关系，如图2所示。

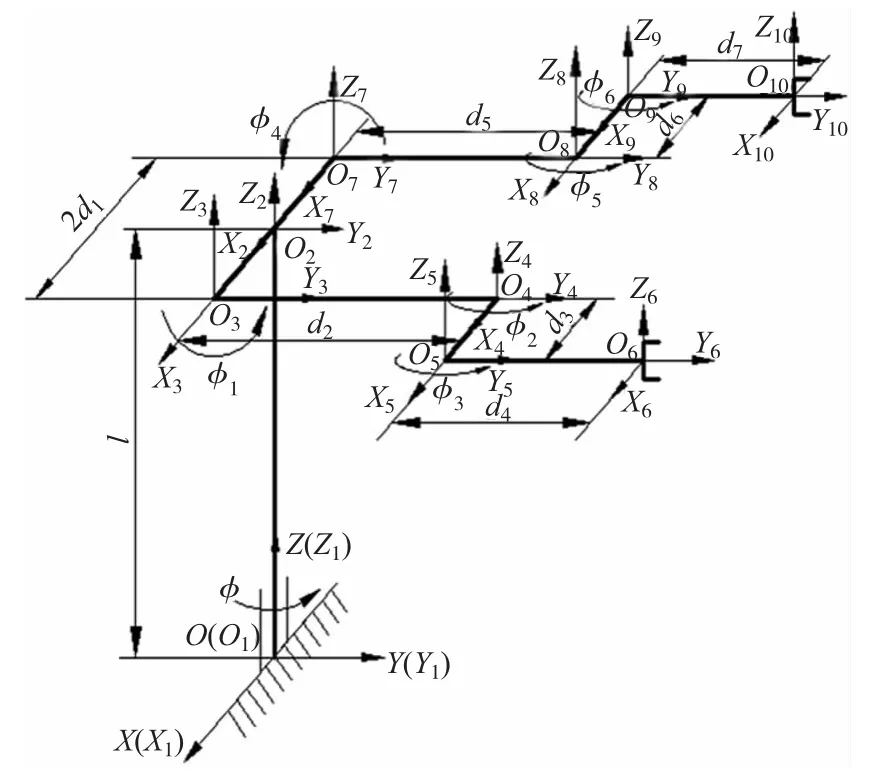
图2 双臂机器人机械臂机构及其杆件坐标

左右两个机械臂都具有基座关节、肩关节、肘关节、横摆关节和末端回转关节5个自由度，这里只研究其前4个关节，因为工作空间仅与它们有关。首先分析各关节参数的约束条件：

（1）关节副转角范围：因结构限制，除基座关节外，其余关节都不能实现全周转动。经分析，确定各关节的转角范围如表1。

（2）杆件长度范围：杆件的长度对机器人的工作空间影响很大。但是，杆件长度同时还受到机器人外形的限制，不宜过长。根据机器人的整体尺寸，各杆长度分别取值为：l=150mm，d1=200mm，d2=d3=d5= d6=300mm，d4=d7=200mm。

表1 机械臂各关节的转角范围

2.2 运动学分析

机器人右单臂各连杆的位姿矩阵为：

发布会现场，中国酒业协会副理事长、秘书长宋书玉宣布了中国葡萄酒感官评价体系评委团组成，并为评委团成员颁发了证书。评委团主席段长青代表行业专家就中国葡萄酒评价体系的建立做了说明和解读。评委团主席：段长青；评委团副主席：王树生、焦复润；评委团委员：李记明、李德美、崔彦志、崔彩虹、孟雷、李泽福。

右机械臂末端作用点（即右机械臂腕关节的中心点）的运动学方程如下：

R—末端作用点相对基坐标系的姿态矩阵；

P—末端作用点相对基坐标系的位置向量，

P=［pxpypz］T。

可知，右机械臂末端作用点的位置向量为：

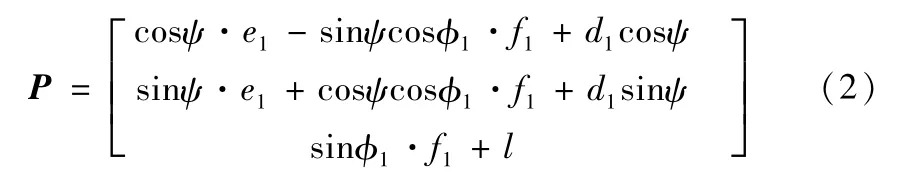
其中，

左臂末端作用点相对基坐标系的位置向量可以用同样的方法求出：

其中，

3 双臂机器人的工作空间分析

3.1 计算方法

双臂机器人可以看作两个单臂机器人的协调工作，其工作空间包括两种：①单臂的工作空间，笔者以前曾对这类空间进行过讨论，这里不再赘述［11］；②双臂的协调工作空间，即两个机械臂末端工作空间的交集。下面提出一种新的方法对这种空间的求解进行探究。该方法的指导思想是：根据单臂的运动学方程和蒙特卡罗法，求出单臂的运动空间，然后建立假想空间网格，并将之细分为很多个子网格，根据点云的分布删除多余的子网格，剩余网格中包含的点云就形成了这种机器人的工作空间。下面是详细的求解步骤：

（1）根据运动学方程，求出单机械臂的末端作用点在基坐标系中的位置向量表达式。

（2）随机点的设定。利用随机函数RAND（j）（j= 1，2，…，N）产生N个0～1之间的随机值，得到机械臂关节变量（即关节转角）的伪随机值为

式中Vi—关节变量的伪随机值；

Vmaxi，Vmini—关节变量的上下限；

i—关节数目。

（3）坐标值的求得。把N个关节变量伪随机值分别代入两机械臂末端作用点的位置向量中，求得两末端作用点的坐标值集合，将其分别存为两个数组；

上述3个步骤与蒙特卡洛法（Monte Carlo method）［12-13］相同。

（4）外包围格的建立。求出两个机械臂分别工作时所共同形成工作空间各方向的最大值和最小值（即两个二维数组各维的最大最小值），此即工作空间的最大值xmax，ymax，zmax和最小值xmin，ymin，zmin。由此可以建立一个长方体，这就是参考点工作空间的外包围格。

（5）子网格的划分。根据精度要求，将外包围格在x、y、z方向边长均匀划分为很多小段。若段数分别为m、n、p，则划分后每段的宽度应为

据此对步骤（4）建立的外包围格剖切，可得m×n×p个小长方体，即子网格。

（6）多余空间子网格的去除。采用遍历搜索算法，对每一个空间子网格进行分析，上述坐标点是否落在其中。如果只有一个数组的坐标值在其中，则将该网格存入该数组坐标对应的单臂子网格集合中；如果该网格有两个数组的坐标值，就存入双臂协调子网格集合中；对于没有内部点的网格，舍弃。将双臂协调子网格集合中网格包含的坐标点描绘在基坐标系中，就得到协调工作空间的云图。

3.2 工作空间的仿真与分析

取随机值N=40000个，可得该机器人两机械臂的工作空间云图。图3～图5是末端作用点工作空间在基坐标系中的形状云图。

按照前述机器人的抓取步骤，机器人到达目的地后先转动基座关节摆正姿势，此后基座关节一般不再转动，因此，必须分析基座关节不动时两机械臂的工作空间。图3给出了基座关节不动时左、右两机械臂各自的工作空间三维形状。图4则示出了基座关节不动时左、右两机械臂的协调工作空间三维形状，从图中可以看出，协调工作空间的范围比两臂独立工作时的空间的范围缩小了很多，而且无法实现全周覆盖。图5显示的是基座关节可以转动时左、右两机械臂的协调工作空间三维形状，由图可知，在这种情况下，协调工作空间可以实现以机器人为中心的全周覆盖，因此，前述双臂机器人的结构能满足使用要求。

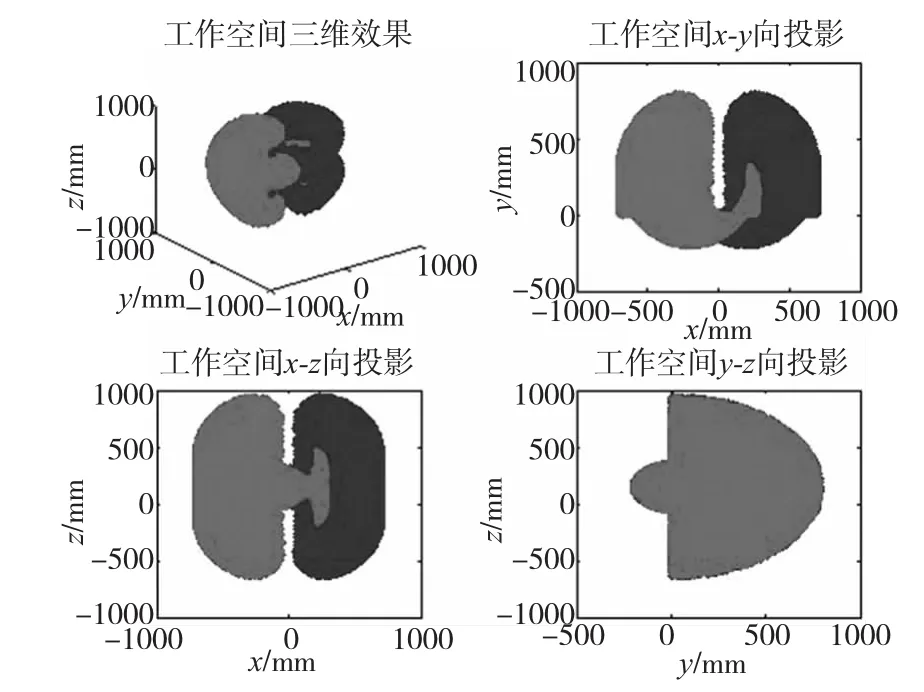
图3 基座关节不动时两机械臂各自的工作空间

图4 基座关节不动时两机械臂的协调工作空间

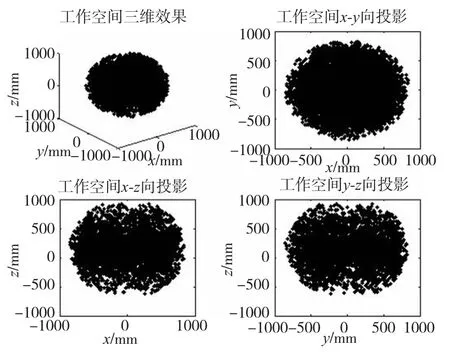
图5 基座关节可转时两机械臂的协调工作空间

4 结束语

提出一种双臂移动机器人的主要结构，经过简化得到其运动学模型，求出了左右机械臂末端作用点的位置向量。结合蒙特卡洛法和网格划分法，提出一种新的方法，研究这种机器人机械臂的工作空间问题。根据机器人的工作特性，首先得到了在基座关节不动时两机械臂独立工作时的工作空间点云图和协调工作空间点云图。然后，求出了基座关节可以转动时两机械臂的协调工作空间点云图。结果表明，在基座关节可以转动的情况下，协调工作空间能够实现对机器人的全周覆盖，可以满足使用要求。

［1］张洁，李艳文.果蔬采摘机器人的研究现状、问题及对策［J］.机械设计，2010，27（6）：1-5.

［2］张文辉，叶晓平，季晓明，等.国内外空间机器人技术发展综述［J］.飞行力学，2013，31（3）：198-202.

［3］李斌.月球车车载机械臂的研究进展及关链技术探讨［J］.机器人技术与应用，2008（3）：29-32.

［4］吴伟国，吴鹏.基于避障准则的双臂手移动机器人桁架内运动规划［J］.机械工程学报，2012，48（13）：1-7.

［5］李瑞峰，马国庆.基于Matlab仿人机器人双臂运动特性分析［J］.华中科技大学学报，2013，41（s）：343-347.

［6］Abdel-Malek K，Yeh H J.Analytical boundary of the workspace for general 3-DOF mechanisms［J］.The international Journal of Robotics Research，1997，16（2）：198-213.

［7］Botturi D，Martelli S，Fiorini P.A Geometric method for robot workspace computation［C］.The 11thInternational Conference on Autonomous Robots and System.Verona：Verona University Publications，2003.

［8］张建业，赵臣，张宏杰，等.正交机器人机构工作空间的数值算法［J］.天津大学学报，2013，46（10）：862-866.

［9］许卫斌，平雪良，应再恩，等.6R型串联机器人工作空间快速求解方法机械设计，2013，30（6）：28-31.

［10］Prince C.Progressive meshes for large models of arbitrary topology［D］.Seattle：University of Washington，2000.

［11］田海波，马宏伟，魏娟.串联机器人机械臂工作空间与结构参数研究［J］.农业机械学报，2013，44（4）：196-201.

［12］周律，周昱明，汪亮，等.基于蒙特卡罗方法的双臂机器人工作空间分析［J］.机械传动，2014，38（6）：85-87，118.

［13］赵大兴，周小明，李九灵.集装箱喷漆机械手工作空间分析与仿真［J］.机械设计，2008，25（2）：15-17.

（编辑 赵蓉）

Coordinate Workspace Analysis for the Manipulators of a Dual-arm Mobile Robot

TIAN Hai-bo，SHANG Wan-feng，MA Hong-wei
（College of Mechanical Engineering，Xi′an University of Science and Technology，Xi′an 710054，China）

Coordinate workspace for the manipulators of a dual-arm robot is the overlap of left-arm workspace and right-arm workspace，which may imply the flexibility of the dual-arm robot.The main structure of the robot was proposed and its kinematical model was analyzed.Then，the position vector of each manipulator's terminal actuator was taken forward.Based on them，the workspaces were researched by a new method combining Monte Carlo Method and Mesh Generation Method.The cloud pictures of each manipulators workspace and coordinate workspace were completed.The result shows that the coordinate workspace of the manipulators could cover the robot at full range，which can satisfy the requirements.

dual-arm robot；manipulator；workspace；Monte Carlo Method

TH165；TG659

A

1001-2265（2015）06-0020-04 DOI：10.13462/j.cnki.mmtamt.2015.06.006

2015-02-06；

2015-03-26

国家自然科学基金项目（51305338）；陕西省科技统筹创新工程计划项目（2013KTCL01-02）；陕西省自然科学基础研究计划项目（2015JM5235）

田海波（1974—），男，山西长治人，西安科技大学讲师，博士后，研究方向为机器人机构与运动控制等，（E-mail）ttttian-74@163.com。