新课程理念下数学练习设计的有效性探索

☉江苏省无锡市侨谊实验中学　程燕英

☉江苏省无锡市金星中学　朱宸材

新课程理念下数学练习设计的有效性探索

☉江苏省无锡市侨谊实验中学程燕英

☉江苏省无锡市金星中学朱宸材

传统数学教学比较注重教师对于知识的特定固有化训练，并不太注重学生情感、态度和价值观在教学中的体现.笔者思索自己在学生时代的数学学习，教师在课堂上将数学的定义给出，而后提出几项关于定义的注意要求，然后按照书本上的例题进行简单的讲解，而后以教材后续的练习进行训练，这是留在笔者脑海中新知教学的大致印象.时至今日，回想这样的照本宣科式教学，笔者思考：这样的教学似乎并不太关注学生学习是否高效和有效，也没有针对合理的学情进行有效的练习设计，更谈不上教学是否达到了以生为本、注重建构的教学理念！

另一方面，新课程实施后的数学教学也让我们发现了传统教学存在的不少问题.以往教学，我们从不关注以学生的角度思考是否可以轻松吸收这样的形式化数学概念，教师弄懂了，学生实际却大都并不明白.我们也并未对数学练习做过一些深入的思考：这样的练习是否合适？是否符合学校自身的学情？若显得有些难或易，教师应该如何去设计才能让教学变得有效、高效？有时我们做了很多练习但效果甚微，这里深层次的原因思考过吗？笔者认为：因材施教是最好的理由，基于这一理由，对数学练习的设计必须依赖这一原则，符合学情的设计才是最好的设计.

一、数学练习设计的功能

从教师选择和开发来讲，练习设计的功能主要还是下列三个方面，若能做到将这三方面进行有效的整合，这样的练习设计是比较符合新课程理念和时代特征的，是与时俱进的.

（1）反馈功能.练习设计的第一功能即要将学生所学新知进行即时反馈，并且反馈的渠道应该多样化，诸如预习性练习设计反馈、新知类练习设计反馈、变式类练习设计反馈、研究性练习设计反馈、探索性练习设计反馈等，多样化的反馈才能真正了解学生对数学知识的掌握程度，从另一方面来说，教师也可从反馈中不断修正教学的进度和难度.

（2）发展功能.练习设计的要求需要体现对于学生思维达到一定的思维训练，这种思维训练可促进学生了解知识、理解知识、反思知识、巩固知识和运用知识，数学练习设计若按照这种螺旋式上升的层次设计，将会提高学生的思维能力、数学素养，这种发展对于学生继续学习能力的要求是一种促进.

（3）教育功能.练习设计的合理性、逻辑性、高度整合性对于数学学习有着充分的促进作用，从很多教辅资料中笔者发现，数学练习基本是一些所谓的名师在拼凑，这些练习设计根本没有什么逻辑性可言，更谈不上教育功能.笔者对于练习的设计有更深层次的一些想法，即发展学生从特殊到一般、从具体到抽象的认知规律，使其产生对事物研究的一种逻辑感，体现数学练习的教育价值.

二、数学练习设计的探索

对于练习设计的要求，在明确上述功能的基础上，将合理具体根据学情进行实施.笔者结合案例来谈对如何进行练习设计的几种不同探索.

1.一题多解型练习设计

数学练习设计切忌以题论题，否则往往造成知识间缺乏联系性，使得数学学习的效率也大大降低.笔者认为，练习选择要尽可能具备开放性，只有具备开放性原则的练习，才能最大程度地激发学生的大脑思维.这样的练习设计在什么时候使用？笔者的建议是：复习课、探索性课堂、课后练习巩固，这样的问题不宜过多，要做到有而精.

案例1：加工厂生产一种零件，有如下规定：∠A、∠B、∠C三个角的度数必须是90°、29°、21°，若检测人员通过测量∠DCB=141°的方式就可以判别此零件为不合格品，请大家想想检测人员这种判断的依据是否合理，并说明理由.

说明：这是依据苏教版七年级下册教材改编而设计的一道数学练习.主要目的是通过一题多解的方式培养学生的开放性思维，追求不同的解决问题的方式.

探索1：如图2所示，连接BD，则∠ADB+∠ABD=90°，而∠ADC+∠ABC=29°+21°=50°，所以∠CDB+∠CBD= 90°-50°=40°，所以∠DCB=180°-40°=140°，因此标准尺寸应是140°，141°不符合要求.

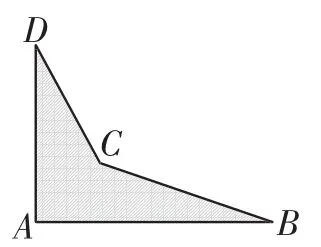
图1

图2

图3

探索2：如图3所示，延长DC交AB于E，则∠AED=90° -29°=61°，∠CEB=180°-61°=119°，故∠DCB=∠BEC+∠B=119°+21°=140°，所以141°不符合要求.

探索3：如图4所示，连接AC并延长到E，则∠BCE=∠BAE+∠B，∠DCE=∠DAE+∠D，所以∠BCD=∠BCE+∠DCE=∠BAE+∠B+∠DAE+∠D=∠A+∠B+∠D=90°+ 21°+29°=140°，所以∠DCB是141°不符合要求.

探索4：如图5所示，作DE∥AB，CF∥AB，则DE∥CF.所以∠FCB=∠B=21°，∠EDC=90°-∠ADC=61°，∠DCF= 180°-61°=119°，所以∠BCD=∠FCB+∠FCD=21°+119°= 140°，所以141°不符合要求.

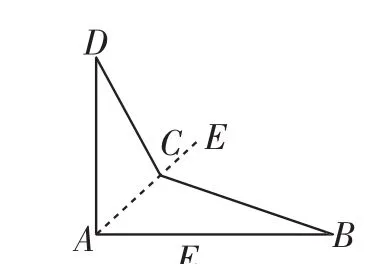
图4

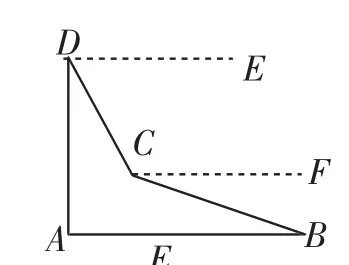
图5

探索5：不需连线，考虑到四边形ABCD的内角和为360°，而360°-29°-21°-90°=220°，所以∠DCB=360°-220° =140°，所以141°不符合要求.

说明：本题的设计初衷是希望通过一题多解的方式，让学生在解决问题过程中回顾多种知识，通过实践，笔者发现学生对构造三角形、利用平行、利用内角和等多种方式进行了剖析，可见这样的数学练习设计是符合新课程自主探索、积极建构的理念的，是一种较为有效的练习设计.

2.一题多变型练习设计

无独有偶，仅仅依赖一题多解还无法形成知识的全方位梳理，将一题多变引入到练习设计中，恰恰达到了这样的效果.一题多解和一题多变正如横向与纵向的交叉整合，达到了另一种发展能力的培养要求.

案例2：（1）如图6，在△ABC中，∠BAC是直角，AB= AC，点D在BC上，且BD=BA，点E在BC的延长线上，且CE=CA，试求∠DAE的度数.

（2）如果把（1）中“AB=AC”这个条件舍去，其余条件不变，那么∠DAE的度数会改变吗？

（3）如果把（1）中“∠BAC为直角”这个条件改成“∠BAC为钝角”，其余条件不变，那么∠DAE与∠BAC有怎样的大小关系？请说明理由.

另深入研究：若将“∠BAC为直角，AB=AC”都去掉，（3）中的关系仍成立吗？

解析：结论仍成立.

若设∠B=x，∠ACB=y，则∠BAC=180°-x-y.由BD= BA，得

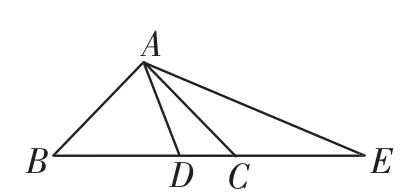
图6

变式1：小王和小张在解这

样一道题：“如图7，在△ABC中，∠BAC为直角，点D、E在边

BC上，AB=BE，AC=CD，求∠DAE的度数”.他们分别经过

计算后，结论不一致，小王说：“∠DAE的值与∠B有关，只有告诉∠B的度数才能求出∠DAE的度数.”小张说：“∠DAE的度数是一个定值，与∠B的度数无关.”你能告诉我们谁说正确了吗？请说明理由.

图7

解：设∠B=x.由∠BAC=90°，得∠C=90°-x.由BA=x.由CA=CD，得∠CDA=45°.因此，小张的说法是正确的.

变式2：若将拓展中的“∠BAC=90°”去掉，那么∠DAE与∠BAC有怎样的数量关系呢？

解：设∠B=x，∠ACB=y，则∠BAC=180°-x-y.由BA= BE，得x.由CA=CD，得∠CDA=

变式3：如图8，在△ABC中，D、E在直线BC上，且DB= BA，CE=CA，试确定∠DAE与∠BAC的关系.

解：设∠ABC=x，∠ACB=y，则∠BAC=180°-x-y.由 DB=BA，得∠D=∠DAB=

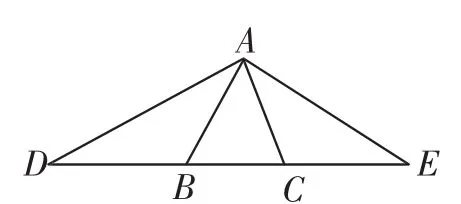
图8

说明：变式型的数学练习设计是一种思维广度的训练，在这种思维广度训练中，教师在引导学生，涉及的知识点是在具体问题情境中给予展示的，这种练习对于学生解决问题思维的全面性是一种有效的促进.

三、数学练习设计的思考

数学练习设计是新课程理念下的新生研究对象，相比传统教学，新课程下的数学教学对于很多方面的要求提出了更为专业化、细致化的实施和操作.笔者思索，当下的数学教学犹如一种科技公司的生态圈，将各种教学设计得更为精细和专业，成为形成整个数学教学的完整生态圈.这其中，数学练习设计成为该生态圈不可分割的重要组成部分.对于数学练习设计，笔者还有下列一些思考.

（1）校本化趋势.数学练习设计有多重形态，有预习性练习设计、新知类练习设计、变式类练习设计、研究性练习设计、探索性练习设计等，相对而言，这些练习设计必须依赖教师的现成开发，不可能也没有现成的资料可以直接使用.笔者认为这种现行的开发愈来愈呈现一种校本化的姿态，以符合学情开发的练习设计成为一种趋势.

（2）多元化倾向.文中所列举的案例采用了两种较为符合现阶段教学的方式，即一题多解和一题多变练习设计，这两者设计类似于纵向和横向的知识梳理，将练习设计的基准化建立了起来.后期练习设计还可以更追求发展化、卓越化，笔者以为可以采用多元化倾向的设计思路，具体的实施形态上可以知识拓展的方式去呈现，比如学生参与的练习设计尝试，这种方式对学生的知识体系要求会更高，将优秀学生对知识的认知达到了更高的境界和要求，这正体现练习设计的能力化要求.

（3）高效化手段.练习设计的最现实要求是学生是否可以最高效地解决数学问题，这是有效性教学的体现、高效性教学的根本.笔者思索，以教材为本设计的练习设计，从基本知识和基本技能上讲已经成功地解决了学生的双基，以校本化设计的练习从能力上解决了学生应试的一些基本素养，除此之外，学生并不需要大量额外的练习去占用学习时间，是一种高效教学手段的呈现.

上述是笔者以自身的一些经验和案例实践为本，阐述了练习设计有效性探索的初步尝试，与大家交流，恳请提出宝贵意见.

1.许盈.拓展学生的三个发展空间，培养创新意识［J］.中学数学教学参考，2003（5）.

2.吕立杰，马云鹏.情境教学和小组讨论［J］.教育发展研究，2002（10）.

3.张奠宙，李士锜，李俊.数学教育学导论［M］.北京：高等教育出版社，2011.Z