模块化双足机器人运动学模型研究

邓三鹏，杨文举

（天津职业技术师范大学 机械工程学院，天津 300222）

0 引言

双足机器人是机器人研究领域最前沿的问题之一，它集机械、电子、计算机、材料、传感器、控制技术及人工智能等多门学科于一体，反映一个国家智能化和自动化研究水平，同时也是一个国家科技实力的重要标志[1]。双足机器人的关键技术是对机器人步行技术的研究，而机器人的步行运动是一种高度自动化的运动，具有非常复杂的动力学特性以及很强的环境适应性[2]，相对轮式、履带式机器人，双足机器人有无可比拟的优越性，具有广泛的应用前景[3]。为了能够对双足机器人进行高度自动化控制，对机器人本体建立正确的运动学模型是首要的，同时建立正确的运动学模型也是其他所有运动学和动力学分析的基础。采用模块化机器人套件搭建出双足机器人本体，依据本体参数分别对手部和脚部建立基于躯干中心的运动学模型，并对该模型进行验证，为依据于该双足机器人的其他运动学、动力学仿真和分析打下基础，也为同类型机器人运动学模型的建立提供一定参考。

1 双足机器人本体设计

利用创意之星模块化机器人套件[4]，模拟和参考人的手臂和腿部结构，设计并搭建出多个自由度的双足机器人。根据模块化机器人套件提供的结构件，简化设计双足机器人手臂和腿部关节。各关节采用舵机控制，其中手臂由三个舵机控制，腿部由四个舵机控制。驱动舵机采用组件提供的固定构件固定在手臂或腿部的结构件上，然后依据人体比例对手臂和腿部的结构件长度进行调整，最后利用结构件将手臂和腿部固定在机器人躯干上，躯干为模块化双足机器人控制器及电源。搭建好的模块化双足机器人结构如图1所示。

图1 模块化双足机器人本体

2 双足机器人运动学建模

机器人的运动学模型是机器人运动学、动力学仿真分析和步态规划的基础。依据搭建好的模块化双足机器人实物模型尺寸，利用D-H法则建立运动学模型如图2所示。

图2 双足机器人关节坐标系

其中左臂和左腿的模型建立方式与右臂和右腿对称，图中予以简化。机器人位姿数学模型建立时，各个坐标系原点选定在同一平面内。为有利于对机器人进行运动学分析，机器人的固联坐标系原点设其在躯干中心，原点水平向右为Z轴正向，机器人前进方向为X轴正向，垂直向上为Y轴正向。依据D-H法则建立的其他关节坐标系Y轴方向（图中未标出）利用右手定则进行判断。

选取机器人右臂和右腿（左臂和左腿与右臂和右腿的模型建立方法相同，这里不再赘述），以机器人本体中西坐标系为固联坐标系，利用D-H法则分别建立运动学模型。基于建立的运动学模型后，根据转动关节连杆四参数图（图3）所示[5]，利用如下规则确定机器人相邻两连杆之间的相对关系：

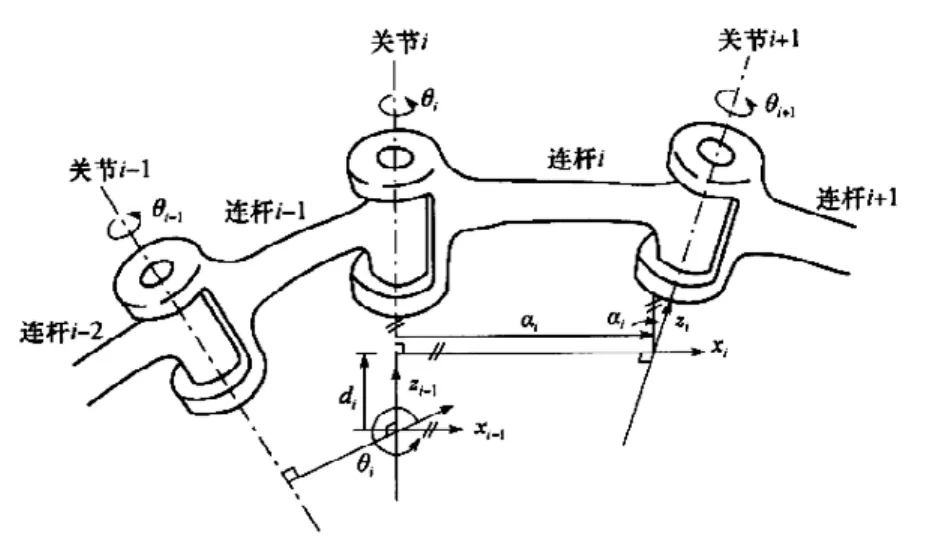
图3 转动关节连杆四参数图

1）绕zi-1轴旋转θi角，使xi-1轴与xi在同一平面内；

2）沿zi-1轴平移距离di，使xi-1轴与xi重合；

3）沿xi-1轴平移距离ai，移动连杆i-1的坐标系使两坐标系原点重合；

4）绕xi-1轴旋转ai-1使zi-1轴与zi重合。

通过对实物模型的测量及分析，得到人型机器人各个连杆关节的长度后，确定机器人手臂连杆参数如表1所示。

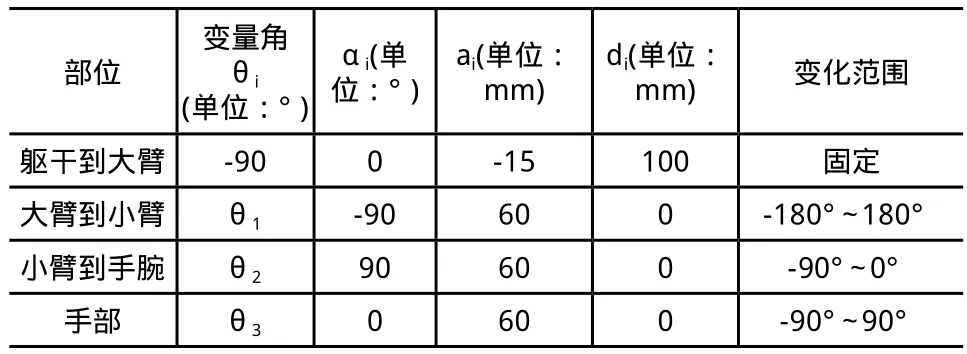
表1 机器人手臂连杆参数

根据手臂连杆参数，计算得到连杆之间的变换矩阵分别为1T2，2T3，3T4，4T5（si,ci分别表示sin θi，cos θi，i=1,2,3,4,5,6,7）。

则机器人躯干坐标系O1到手部末端坐标系O5的位姿正解表达式为：

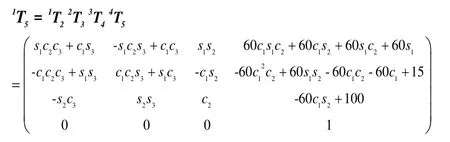
机器人腿部连杆参数如表2所示。

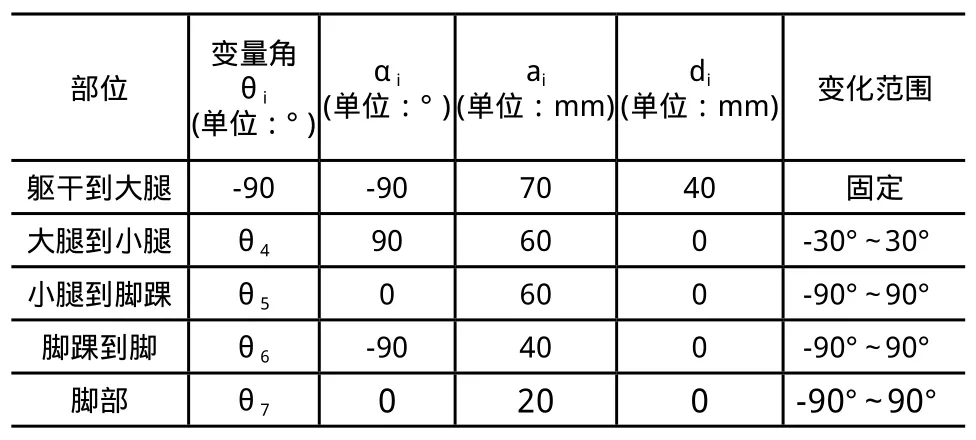
表2 机器人腿部连杆参数

依据机器人腿部连杆参数表，计算得到腿部连杆之间的坐标系变换矩阵1T6，6T7，7T8，8T9，9T10，结果分别为：

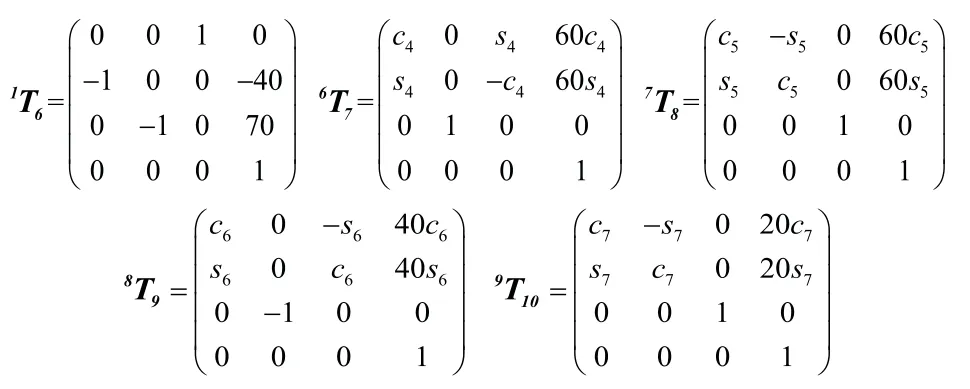
则机器人躯干坐标系O1到脚部的坐标系O10的变换矩阵为：

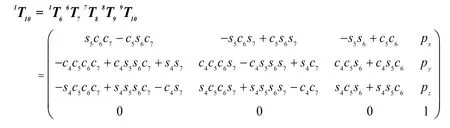
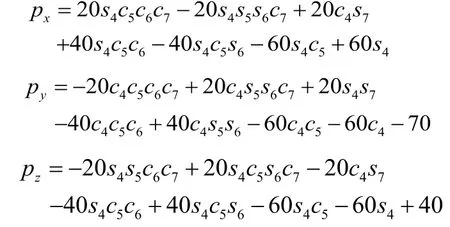
其中：为验证机器人手部位姿正解矩阵1T5和脚部位姿正解矩阵1T10的正确性，首先计算初始状态下机器人位姿。取θ1=θ2=θ3=θ4=θ5=θ6=θ7=0，计算正解矩阵1T5和

1T10，其结果分别为：

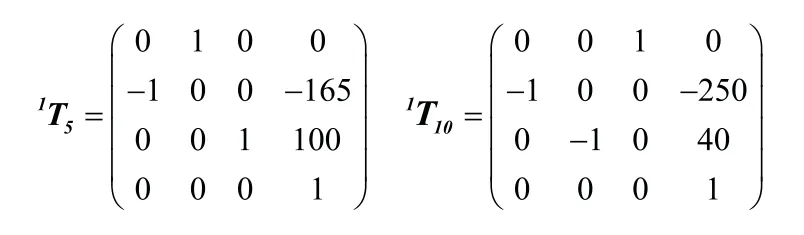
由图2可知，依据D-H法则建立的机器人躯干坐标系O1经过变换矩阵1T5变换后得到的坐标系与机器人手部位姿坐标系O5一致，经变换矩阵1T10变换后得到的腿部坐标系与机器人腿部位姿坐标系O10位姿相同。其次，固定机器人躯干，对手臂和腿部各关节取多组数值，在ADAMS软件中对机器人三维模型进行仿真验证，部分验证实验结果如图4所示。

图4 仿真实验图

依据双足机器人初始位姿正解矩阵的求解计算以及在ADAMS中对三维模型进行仿真验证，该双足机器人运动学模型正确。

手部变换矩阵1T5和腿部变换矩阵1T10分别描述了双足机器人手部末端坐标系O5和脚部末端坐标系O10相对于机器人躯干坐标系O1的位姿数学模型，这两个位姿模型是机器人运动学分析和综合的基础。

3 结论

1）依靠模块化机器人组件能方便迅速的搭建机器人模型这一优势，搭建出了具有多个自由度的模块化双足机器人，其在一定程度上对人的脚部和手臂结构进行了模拟。

2）基于模块化机器人组件搭建的双足机器人本体模型，分别建立了机器人手臂的末端坐标系和腿部末端坐标系相对于躯干坐标系的位姿数学模型，在该基础上，通过对双足机器人初始位姿正解矩阵的求解计算，以及在ADAMS中对三维模型进行仿真验证，验证该双足机器人运动学模型正确。此模型是基于该机器人运动学分析、步态规划、动力学分析的基础，也可以作为同类型机器人建模的参考，具有一定意义。

[1] 俞志伟.双足机器人仿生机构设计与运动仿真[D].哈尔滨工业大学,2006.

[2] 朱晓光.双足机器人步态与路径规划研究[D].华北电力大学,2012.

[3] 史耀强.双足机器人步行仿真与实验研究[D].上海交通大学,2008.

[4] 姚宪华,梁建宏.创意之星模块化机器人创新设计与竞赛[M].北京:北京航空航天大学出版社,2010.

[5] 蔡自兴.机器人学基础[M].北京:机械工业出版社,2009.

[6] Nada Kherici.Using PSO for a walk of a biped robot.Annaba[J].Journal of Computational Science 5 (2014): 743-749.

[7] H.Kimura, S.Shimoda, Reflex-type regulation of biped robots, in:X.Hu, U.Jonsson, B.Wahlberg, B.Ghosh (Eds.)[J].Three Decades of Progress in Control Sciences, Springer, Berlin/Heidelberg,2010:249-264.

[8] X.Zhou, Y.Guan, C. Cai, L.Jiang, H.Zhu, X.Zhang, Modeling and planning forstable walking of a novel 6-dof biped robot[J].2010 IEEE International Conference on Robotics and Biomimetics(ROBIO), 2010:7-12.

[9] 梁青,宋宪玺,周烽,等.基于ADAMS的双足机器人建模与仿真[J].计算机仿真,2010,27(5):162-165,238.