面向冗余驱动的自适应柔性连接机构优化设计

杨国军，杨桂林，王福明

（1.中北大学 机械与动力工程学院，太原 030000；2.中科院宁波工业技术研究院，宁波 315201）

0 引言

作为一种结构简单，成本低廉的自动化机器人解决方案，X-Y-Z直角坐标机器人[1]被广泛应用于点胶、码垛、分拣、包装、装配等工业生产领域。传统X-Y-Z直角坐标机器人直线运动单元的实现多数通过一台伺服电机并配有滚珠丝杠、同步带或者齿轮齿条来实现[2]。比如德国百格拉公司生产的用于汽车涂胶、注液和装配车轮的直角坐标机器人[3]。还有广泛应用于卧式数控车床上下料的直角坐标机器人[4]。但是由于有传动装置，导致无法达到很高的运动速度和精度。

我们研发的X-Y-Z直角坐标机器人在X方向采用了直驱技术（X方向采用两个直线电机同时驱动的对称设计），不仅在很大程度上提高了运动的速度和精度，还减少了机械传动零件，减少了磨损，提高了设备寿命，如图1所示。

图1 X-Y-Z直角坐标机器人

但是由于X方向的直线电机和Y方向的横梁之间是刚性连接，如图2所示。采取这样的连接方式会形成冗余驱动。当X方向两个电机不同步时会产生诸如一前一后等运动干涉，从而影响运动的平稳性。

图2 刚性连接

为了能够进一步提升该X-Y-Z直角坐标机器人的运行速度，使运动更加平稳，我们采用柔性关节将刚性连接的冗余驱动转变为具有确定性运动的柔顺驱动。

1 连杆机构型综合

根据运动的性质和自由度，该X-Y-Z直角坐标机器人在X方向有两个直线电机驱动，只有一个自由度。所以我们考虑增加一个自由度来消除冗余驱动。由于五杆运动链是构成两个自由度的机构运动链中最简单的运动链，从最基本的全为转动副（RRRRR）的五杆机构到全为移动副（PPPPP）的五杆机构之间，通过排列替换R和P接头进行拓扑分析，可以得到很多种不同类型的五杆机构[5,6]。

该直角坐标机器人X方向的两个直线电机（沿X方向做往复直线运动）转化为两个P关节，Y方向横梁分别与X方向两个电机之间的刚性连接可以转化为PPP、PRP、RRR等关节。由于X-Y-Z直角坐标机器人在X方向运动不平稳时，该刚性连接既有沿着横梁方向的微小变形又有绕Z方向的微小转动。所以我们通过一侧采用一个PR关节，另一侧采用一个R关节，构成PRPRP五杆机构，从而替换掉两侧的两个刚性连接，来消除冗余驱动，如图3所示。

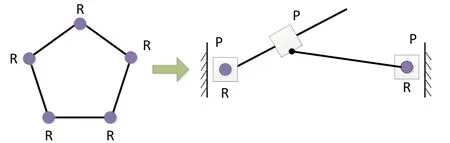
图3 五杆机构拓扑分析

2 柔性关节设计

柔性关节作为一种小体积、无机械摩擦、无间隙和运动灵敏度高的传动结，广泛应用于各种要求微小线位移或角位移、且高精度高分辨率定位的场合[7,8]。

如图4所示，我们采用了两个十字交叉的弹簧片式的柔性关节，它是一个R关节。当我们把这两个柔性关节分别替换X-Y-Z直角坐标机器人两个刚性连接后，两个R就会额外产生一个微小位移，也就是形成一个P关节，构成RPR，所以没必要一侧专门采用一个RP关节。该柔性关节的两个相互垂直的弹簧片分别连接两个块，一个块固定到Y方向的横梁，一个块固定到X方向的直线电机上。

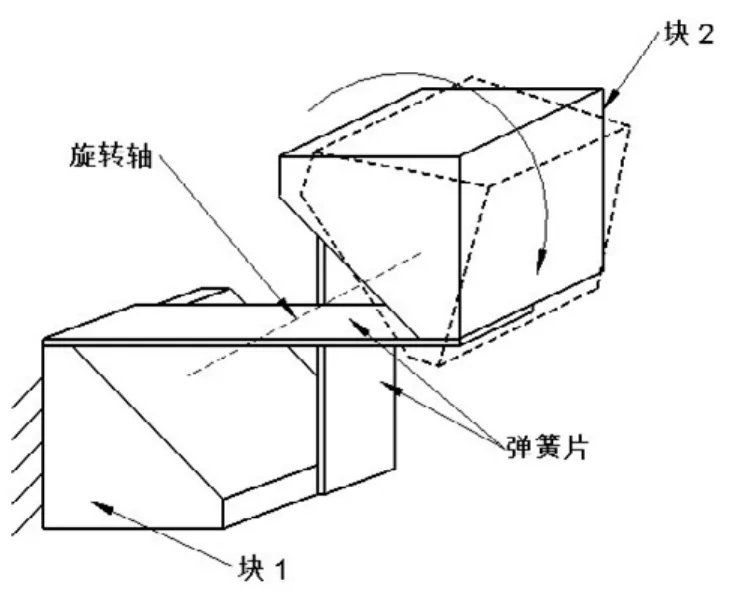
图4 弹簧片十字交叉的柔性机构

3 系统性能要求

系统性能要求是：把该X-Y-Z直角坐标机器人X方向的电机和Y方向的横梁之间所采用的刚性连接换为此柔性关节后，整个系统在X、Y、Z方向的变形要很小，不能大于5个微米。X方向两个电机在不同步时所产生最大相对位移不超过2mm情况下，克服X方向两个直线电机由于不同步所产生的驱动力的力差要小。也就是使整个系统在X、Y、Z方向的刚度要很大，而在X方向的驱动刚度要很小，即kx,ky,kz要大，k'x要小，最后建立出反映系统性能要求的目标函数，如公式(1)所示：

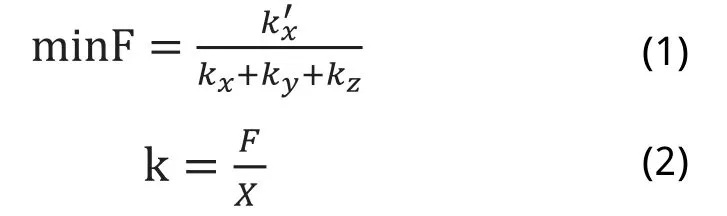
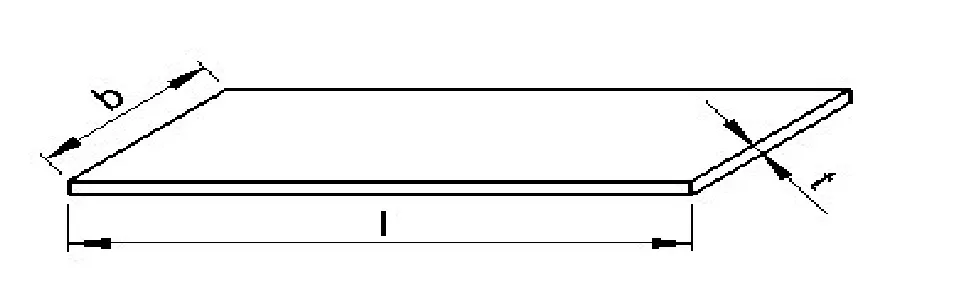
图5 柔性机构弹簧片

4 仿真模型建立

把该柔性关节的三维模型取代刚性连接安装到X-Y-Z直角坐标机器人内，建立有限元仿真模型，如图6～图9所示。

图6 Z方向变形仿真模型

图7 Y方向变形仿真模型

图8 X方向变形仿真模型

图9 相对位移为2mm时的力差

5 柔性关节尺寸优化设计

我们采取正交优化算法来给出柔性关节最优设计尺寸。试验因素有弹簧片的长度l，宽度b，厚度t，每个因素选择了三个水平进行考察，如表1所示。该柔性机构的正交优化试验是一个3因素3水平L9(33)的正交试验设计问题。

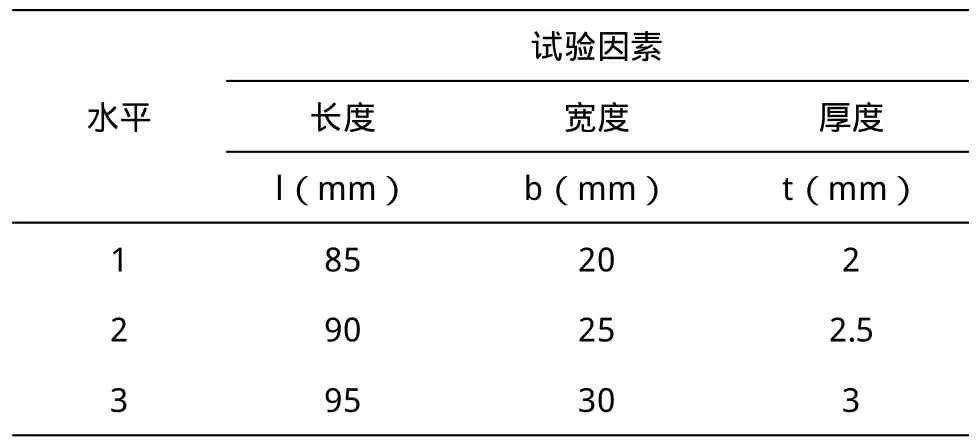
表1 三因素三水平表

利用ANSYS有限元分析，得到9组l、b、t对应下的有限元分析结果，如表2所示。

根据正交试验结果和公式(1)，公式(2)得到9组目标函数值，以曲线形式表示，如表3所示。从表中可以看到当试验次数是6时得到的目标函数值最小为4.462×10-6。

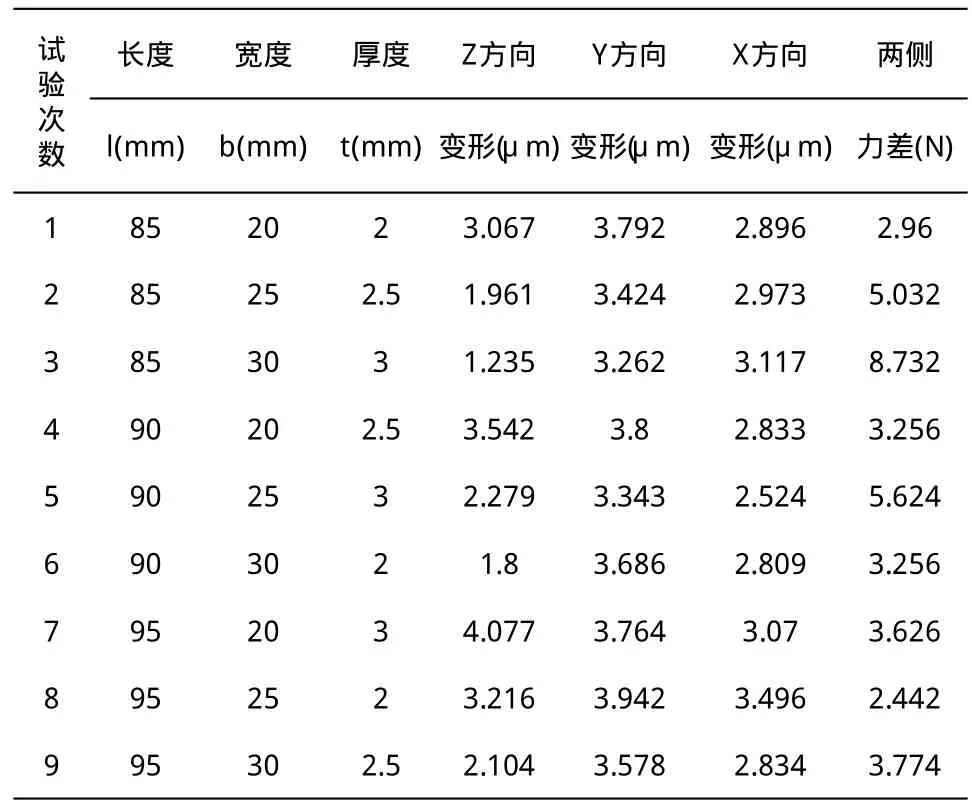
表2 试验结果

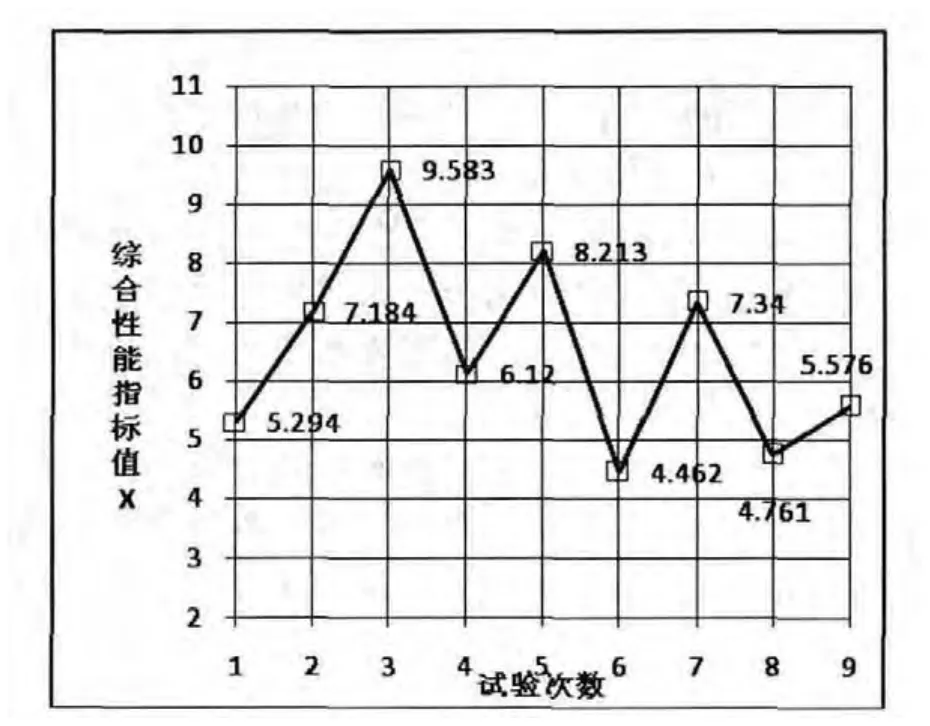
表3 各试验次数下目标函数值

建立目标函数值极差分析表，如表4所示。我们可以看到厚度对目标函数值影响最大，宽度影响最小。可以回归出，l取95mm，b取20mm，t取2mm时为最优组合。

表4 目标函数值的极差分析表

6 有限元仿真验证

为了验证该柔性关节参数的正交优化设计方案，根据这组最优参数进行了三维建模，如图10所示。把该柔性机构安装到系统中进行了有限元分析验证。

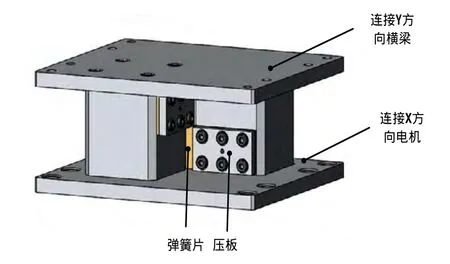
图10 最优设计参数下的柔性机构

得到整个系统在X方向的变形最大为3.87微米，如图11所示。整个系统在Y方向的最大变形为4.347微米，如图12所示。整个系统在Z方向的最大变形为4.684微米（由于坐标系中的Z轴正好是Z方向所施加力的反方向，所以最大变形看蓝色），如图13所示。在X方向的两个电机在不同步时所产生的最大相对位移为2mm，（如图14所示，1.942微米可以近似为2mm）的情况下，力差最小为0.0012Mpa，如图15所示，后换算成集中力为1.776N。

图11 X方向的变形

图12 Y方向的变形

图13 Z方向的变形

图14 最大相对位移

图15 最优组合下的力差

根据公式(1)、公式(2)，采取最优参数进行仿真验证后得到minF=4.262×10-6，要比之前9组正交试验目标函数的最小值还要小。说明该组设计参数是最优的一组。

7 结论

1）本文通过柔性连接装置代替刚性连接，解决了X-Y-Z直角坐标机器人的冗余驱动，不仅简化了控制还提升了系统的运动性能。

2）采用正交优化算法，不仅简化了试验次数，还得到了该柔性连接装置的最优设计参数。

3）有限元仿真的结果表明，采用正交优化算法给出的最优设计参数是正确的。

现阶段结构设计已经完成，在制造加工，加工完后我们将安装到机器人内中进行动态性能的测试和分析，进一步优化该柔性结构。

[1] 李刚,周文宝.直角坐标机器人简述及其应用介绍[J].伺服控制,2008,09:72-75.

[2] 赵玉信,沈敏德.直线运动单元技术的应用研究现状与发展前景[J].山东轻工业学院学报(自然科学版),2013,04:54-58.

[3] Philip.百格拉直角坐标机器人用于汽车生产[J].现代零部件,2010,02:26-27.

[4] 李奔.卧式数控车床直角坐标送料机器人的构建方法[J].机械工程师,2012,08:77-78.

[5] 李佳,廖汉元,孔建益,汤勃.平面五杆机构的机构变换及选型[J].中国机械工程,2007,01:20-22.

[6] 赵登峰.平面五杆机构工作空间及其演化的研究[J].机械设计与研究,2007,05:23-25.

[7] 于靖军,裴旭,毕树生,宗光华,张宪民.柔性铰链机构设计方法的研究进展[J].机械工程学报,2010,13:2-13.

[8] Li Yang min, Xu Qing song.Design and analysis of a totally decoupled flexure-based XY parallel micromanipulator[J].IEEE Transactions on Robotics,2009,25(3):645-657.