基于终端滑模控制的两轮移动机器人自平衡实现方法研究

王利清

（包头铁道职业技术学院，包头 014040）

0 引言

两轮移动机器人（又称轮式倒立摆）结构简单、体积较小，可在狭小、危险等环境中运动，故两轮移动机器人在军工、民用、航空航天等领域具有广阔的应用前景[1]。但是两轮移动机器人是一种欠驱动系统，其动力学模型具有不稳定、多变量、强耦合、非线性等特点，因此如何解决两轮移动机器人的控制问题至关重要[2,3]。滑模变结构控制作为一种特殊的非线性控制策略，其滑动模态的设计与对象参数及系统扰动无关，因此滑模控制器响应速度快，系统无需在线辨识，具有较强的鲁棒性[4,5]。与普通的滑模控制相比，终端滑模控制的瞬态性能大幅提高，动态响应速度、跟踪精度、收敛速度均获得了一定程度的改善[6]，因此本文在分析两轮移动机器人动力学模型的基础上，基于终端滑模控制实现两轮移动机器人的自平衡控制，并进行相关仿真研究。

1 两轮移动机器人动力学模型

一般情况下，两轮移动机器人的运动过程比较复杂，很难确定其精确动力学模型，为便于分析，可建立如图1所示的两轮移动机器人简化模型。假设机器人的重心为P点，机器人两侧驱动轮的重心在轮中心。可建立惯性坐标系OX0Y0Z0，以两驱动轮重心连线的中点作为坐标原点；x轴与移动机器人的移动方向重合；y轴与驱动轮轴线方向重合；z轴与竖直方向重合。若忽略机器人侧翻等情况，可建立两个辅助坐标系：偏航坐标系OX1Y1Z1、俯仰坐标系OX2Y2Z2，定义偏航角为α、俯仰角为θ。机器人转向的过程中，左右两轮的旋转角分别用lψ、rψ表示。

图1中相关符号说明如下：1l表示机器人重心与驱动轮中心之间的距离；b表示Ow和O之间的距离；rw表示驱动轮的半径；m1表示机器人质量；mw表示驱动轮质量；Dw表示地面粘滞阻力；D1表示机器人粘滞阻力；lψ、rψ分别表示左右驱动轮的旋转角；Iwa表示驱动轮对轴的惯性矩；Iwd表示驱动轮对直径的惯性矩。

基于拉格朗日运动方程[7]，运动过程中，两轮移动机器人的位置和速度方程可表示为：

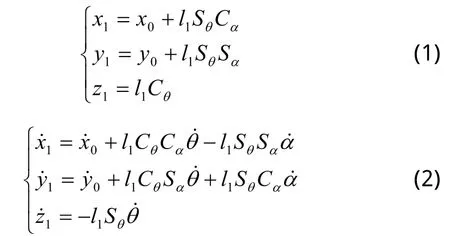
两轮移动机器人的平动动能表达式为：

其中，Tw、Tl分别为驱动轮和机器人本体（不含驱动轮）的动能：

两轮移动机器人的旋转动能表达式为：

其中：

选取移动机器人的驱动轮中心所在平面为零势能面，那么移动机器人的势能可表示为：

运动过程中，摩擦等因素将导致移动机器人系统本身能量的耗散，移动机器人的耗散能可表示为：

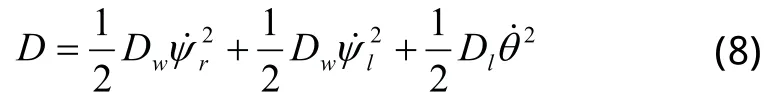
根据拉格朗日动力学方程可得两轮移动机器人的动力学方程为：

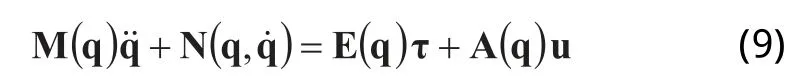
假定移动机器人运动过程中不会出现“打滑”的情况，那么系统约束方程可表示为：

由式(10)可得矩阵A(q)为：

另外，矩阵A(q)的零空间可表示为：

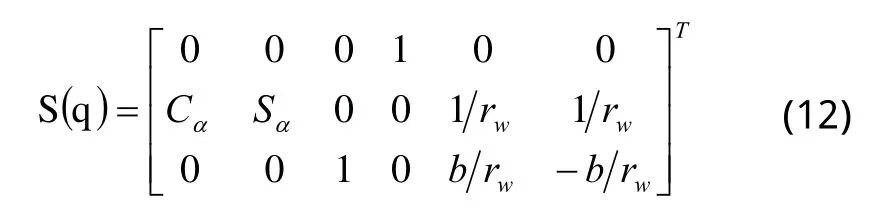
向量q依赖于零空间矩阵S(q)而且满足：

式(13)中，v为移动机器人运动的线速度。

等式(9)两边同时乘以ST，由于STA=0，所以：

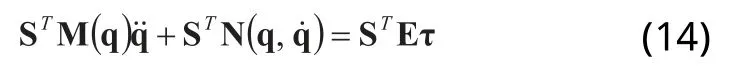
将式(14)代入式(13)可得两轮移动机器人的动力学方程为：

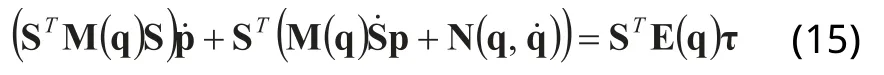
由式(15)可知，移动机器人的动力学方程包含两个驱动力矩和三个自由度，所以该动力学模型为二阶欠驱动系统。

2 两轮机器人终端滑模控制

2.1 终端滑模控制器设计

两轮移动机器人系统的驱动方程为：

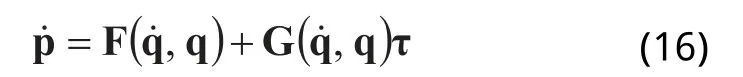
考虑到非线性因素，对应的估计系统为：

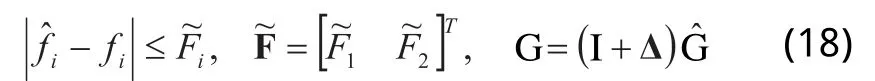
可设计滑模平面[8]：

可设计滑模控制器[9]：

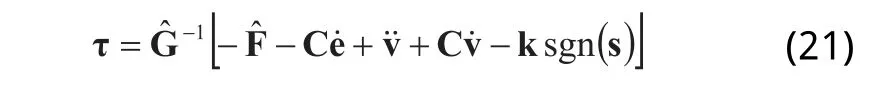
式(21)中：

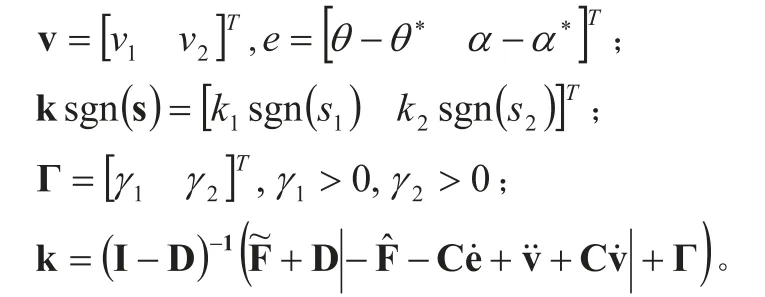
由滑模控制器设计原理可知，滑模控制器(21)可以保证两轮移动机器人系统(16)在滑模面(20)上稳定。

2.2 稳定性分析

定义一个新的矩阵V：

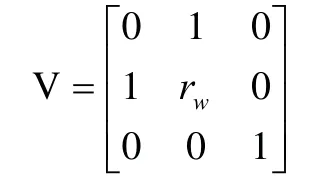
两轮移动机器人动力学方程两端左乘矩阵V可得：

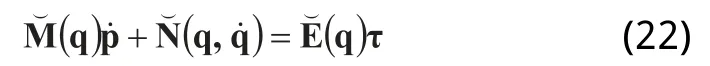
其中：

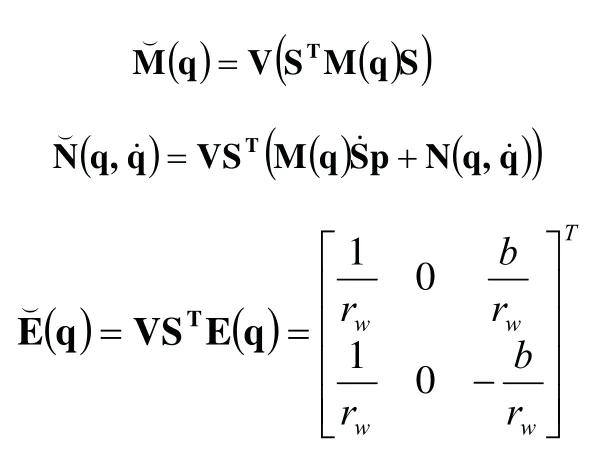
式(22)中的第一项和第三项为驱动方程，第二项为欠驱动方程[10]，可表示为：

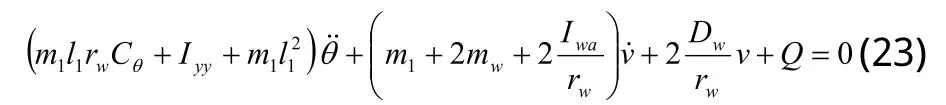
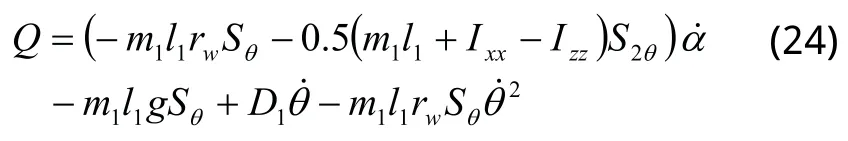
当两轮移动机器人在滑模面上运动时，由式(20)可得：

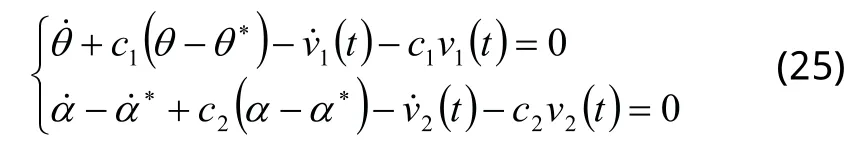
上式中v1、v2表达式已知。设定初始条件的具体数值，即可由式(25)求出和。那么就可以得到关于v的一阶线性微分方程：

其中P(t)为有界函数。式(26)的稳定性与P(t)无关，仅由下式决定：

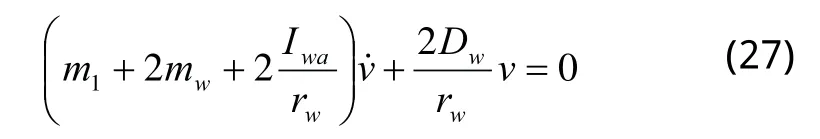
3 仿真实验

为验证本文所述两轮移动机器人动力学模型的正确性以及终端滑模控制方法的有效性，采用MATLAB仿真验证理论分析结果，两轮移动机器人的主要参数如表1所示。

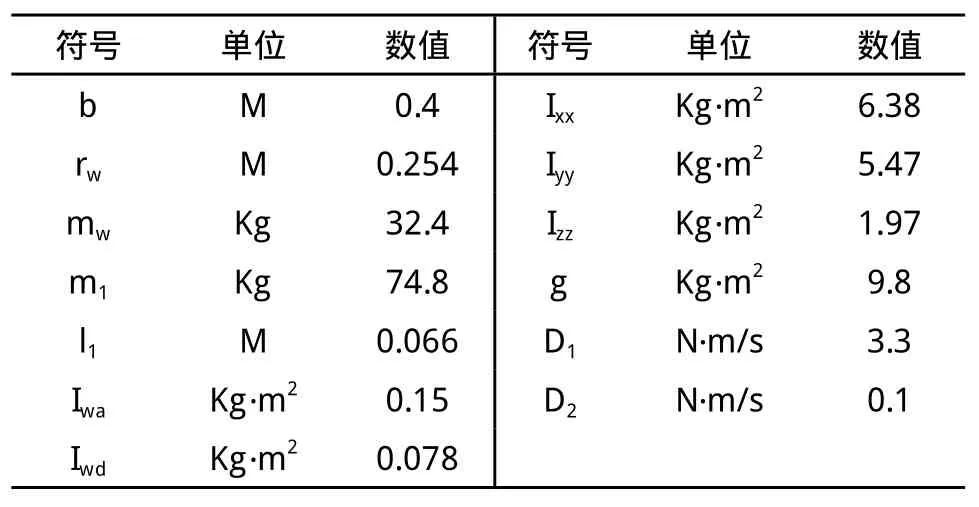
表1 两轮移动机器人主要参数

根据上述分析，滑模平面中的增益方程vi(t)可设计为：

其中：

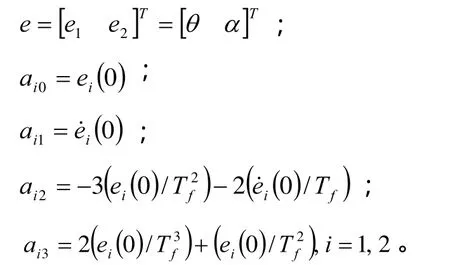
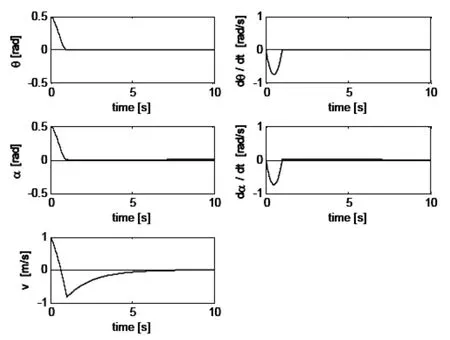
图2 仿真过程中两轮移动机器人系统状态

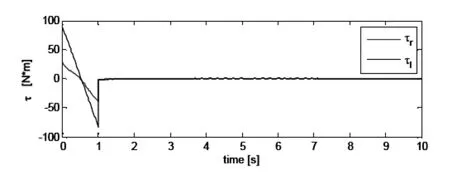
图3 仿真过程中两轮移动机器人输出转矩

4 结束语

本文基于拉格朗日运动方程，推导出了两轮移动机器人的动能、势能等，进而得到了两轮移动机器人的动力学模型。基于滑模变结构控制的基本原理，设计了一种终端滑模控制器，用于两轮移动机器人的自平衡控制，并进行了稳定性分析。最后，针对上述内容进行了仿真实验，仿真结果表明：终端滑模控制器具有较好的控制效果，而且具有较快的收敛速度，可以实现两轮移动机器人的自平衡控制。

[1] Salerno A.,Angeles J.A new family of two-wheeled mobile robots: modeling and controllability[J].IEEE Trans on Robotics,2007,23(1):169-173.

[2] Tsai P. S.,Wang L. S.,Chang F. R. Modeling and hierarchical tracking control of tri-wheeled mobile robots[J].IEEE Transaction on Robotics,2006,22(5):1055-1062.

[3] Liu H., Li J. F. Terminal sliding mode control for spacecraft formation flying[J].IEEE Transaction on Aerospace and Electronic Systems,2009,45(3):835-846.

[4] Guo Y. S., Li C.Terminal sliding mode control for coordinated motion of a space rigid manipulator with external disturbance[J].Applied Mathematics and Mechanics,2008,29(5):583-590.

[5] Sankaranaryanan V.,Mahindrakar A. D.Control of a class of underactuated mechanical systems using sliding modes[J].IEEE Transaction on Robotics,2009,25(2):459-467.

[6] Ferrara A.,Vecchio C.Second order sliding mode control of vehicles with distributed collision avoidance capabilities[J].Mechatronics,2009,19(4):471-477.

[7] Boiko I., Fridman L., Iriarte R.,etal.Parameter tuning of secondorder sliding mode controllers for linear plants with dynamic actuators[J].Automatical,2006,42(5):833-839.

[8] Boiko I.,Fridman L.Analysis of chattering in continuous slidingmode controllers[J].IEEE Transactions on Automatic Control,2005,50(9):1442-1446.

[9] Huang J.,Guan Z. H.,Matsuno T.,etal.Sliding-mode velocity control of mobile-wheeled inverted-pendulum systems[J].IEEE Transaction on Robotics,2010,26(4):750-758.

[10] 傅继奋,孙汉旭,王亮清,等.自平衡两轮机器人的控制系统设计[J].机电产品开发与创新,2004,17(6):75-77.

[11] 李鹏,孙卫蒙,李文强,等.一种改进积分滑模面在飞控中的应用[J].控制工程,2010,17(3):269-273.