拼焊板V形自由弯曲回弹控制影响因素分析
段永川 官英平
燕山大学先进锻压成形技术与科学教育部重点实验室,秦皇岛,066004
拼焊板V形自由弯曲回弹控制影响因素分析
段永川官英平
燕山大学先进锻压成形技术与科学教育部重点实验室,秦皇岛,066004
在平截面和平面弯曲等假设条件下,建立了可适用于纵向拼焊板V形小曲率自由弯曲回弹的解析预测模型。在自由弯曲卸载阶段,该模型引入了两母板间相互作用的弯矩,基于单一母板求解了拼焊板回弹后的弯曲角。利用解析模型分析了不同工艺参数对拼焊板V形自由弯曲力和回弹后弯曲角度的影响规律,确定了影响拼焊板V形自由弯曲力和卸载后回弹角的主要影响因素。
拼焊板;自由弯曲;回弹控制;解析模型;影响因素
0 引言
板材弯曲是板材冲压成形常见的加工工序之一,自由弯曲工艺零件的形状精度和角度精度可以通过控制凸模的位移来实现,大大减少了更换模具的次数。拼焊板V形自由弯曲工艺中,同材差厚拼焊板截面的几何形状和异材拼焊板截面的材料非均质分布都会造成成形力学行为的非对称,加之焊缝、热影响区[1-4]的影响,使回弹控制更加困难。官英平等[5]基于神经网络模型对单板回弹控制进行了研究,在建立回弹控制模型时,需要确定主要控制变量,减小神经网络规模,提高在线神经网络运行效率。因此,在实施拼焊板回弹控制时,通过解析模型构造神经网络样本,并利用解析模型确定各主要影响因素是建立拼焊板V形自由弯曲在线回弹控制模型的关键。
从20世纪开始[6-7],国内外学者对单一板塑性弯曲回弹问题进行了研究,但拼焊板的V形弯曲的回弹解析预测的研究相对较少。姜银方等[8]在假设拼焊板两母板的几何中心重合的条件下,研究了拼焊板V形弯曲回弹预测的解析方法。段永川等[9]考虑截面几何的非对称性,建立了纵向焊缝拼焊板V形自由弯曲回弹的预测模型。该模型在未贴模弯曲中的计算精度较高,但不适于小曲率弯曲回弹预测。因此,本文旨在建立适合拼焊板小曲率自由弯曲回弹的解析预测模型,并利用该模型分析不同工艺参数对拼焊板V形自由弯曲力和回弹后弯曲角度的影响规律。
1 解析分析
拼焊板对齐面朝向凸模成形时,随着凸模行程的增加,凸模下方板料的最小弯曲半径逐渐减小。板料未贴模时的变形如图1a所示,板料贴模时的变形如图1b所示,图1中符号含义参见图2。
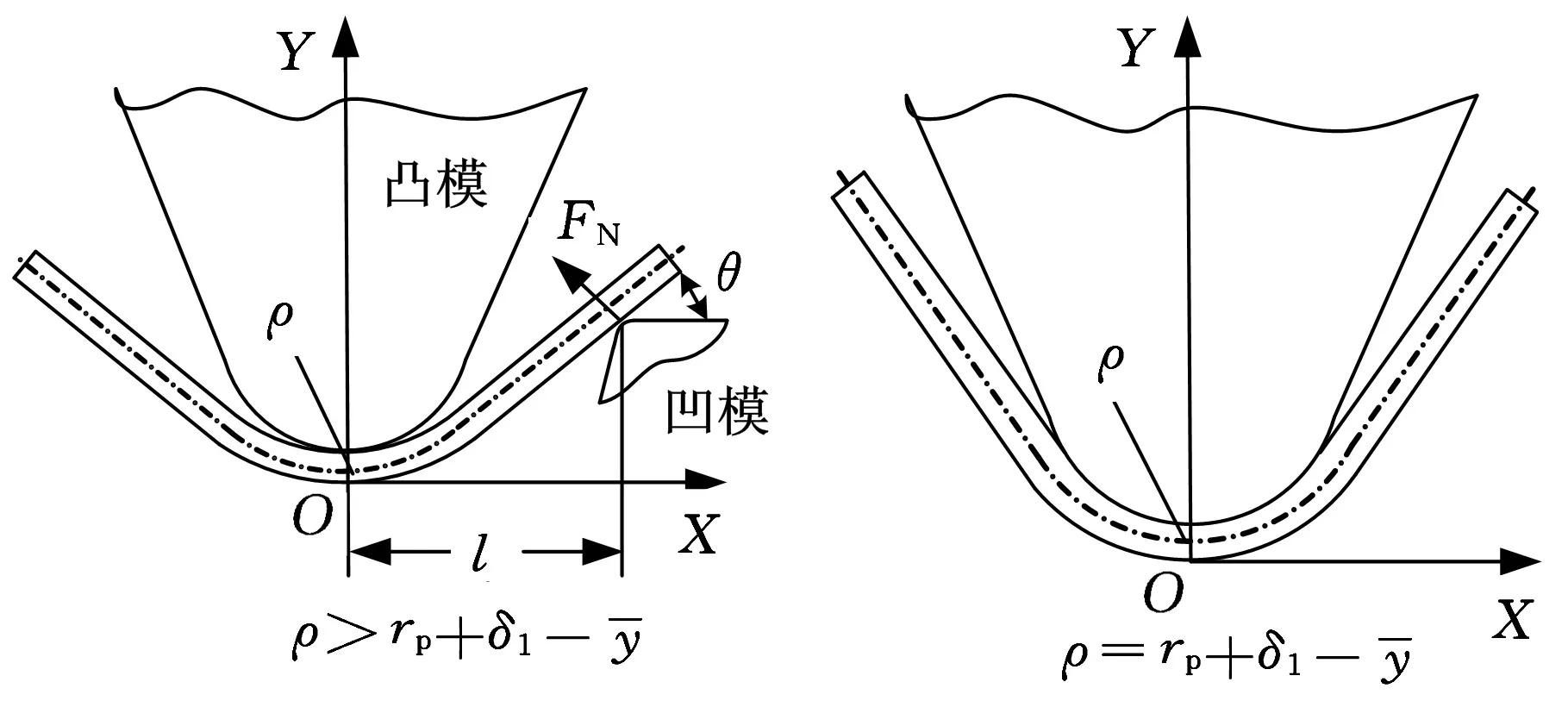
(a)未贴模态(b)贴模态图1 成形过程模具接触状态
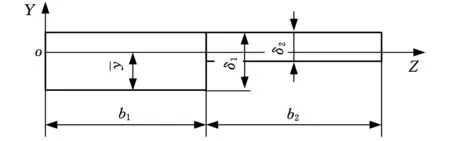
图2 纵向拼焊板截面形状
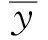
M1=∫S1σxydA=
(1)
M2=∫S2σxydA=
(2)
式中,σx为x方向的应力;K1、K2分别为拼焊板厚侧母板和薄侧母板的强度系数;n1、n2分别为拼焊板厚侧母板和薄侧母板的硬化指数;ρx为拼焊板应力中性层曲率半径;b1、b2分别为拼焊板厚侧母板和薄侧母板的宽度;S1、S2分别为厚侧母板和薄侧母板的横截面积。
根据式(1)、式(2)的积分结果,确定了A1和A2两个中间变量:
(3)
(4)
结合式(1)、式(2)可得拼焊板弯曲过程中的任意一点x处的曲率:
(5)
1.1自由弯曲未贴模成形过程解析
假设作用于纵向拼焊板的弯矩呈线性分布,距离O点为x处的板料截面弯矩为
Mx=FN(l-x)/cosθ
(6)
式中,FN为凹模圆角处法向支撑力;l为凸模圆角中心与凹模圆角中心的距离。
n1=n2,K1=K2时,厚侧母板在任意一点x处的曲率为
(7)
挠度y的二阶导数为
(8)
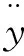
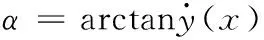
(9)
结合广义虎克定律和式(7)可计算出弹塑性分界点坐标xsm:
(10)
设凸模圆角半径为rp,凹模圆角半径为rd,则凸模的位移h为
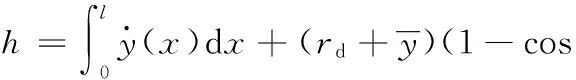
(11)
1.2自由弯曲贴模成形过程解析
1.2.1贴模区域弯矩及曲率的计算
通过式(5)可以得到厚侧母板贴模段(0≤x≤xc)截面弯矩:
(12)
结合式(6)、式(12),可以计算得到
(13)
板料的质点在厚侧母板贴模段时,贴膜段各质点成形弯矩为定值,可得出厚侧母板在任意一点x处的曲率:
(14)
1.2.2未贴模区域弯矩及曲率的计算
假设在xc≤x≤l范围内,板料截面上的弯矩呈线性分布,厚侧母板截面弯矩为
(15)
结合式(5),可得出曲率分布方程:
(16)
此时的凸模位移为
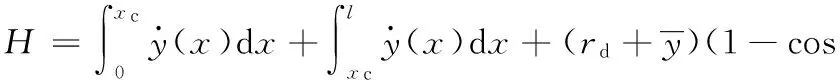
(17)
1.3纵向拼焊板V形自由弯曲弹复过程分析
拼焊板回弹分析过程如图3所示。首先假设两母板卸载时无焊缝变形牵制作用。回弹前的构形为C;卸载后,厚侧板的构形为A,薄侧板的构形为B。根据拼焊板的变形牵制关系,分别对厚侧母板和薄侧母板应用卸载定律得
(18)
(19)
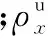
根据式(18)、式(19)可求得相互作用弯矩ΔM,将其代入式(18)可得拼焊板厚侧母板任意一点x处回弹后的曲率半径。根据回弹后的曲率半径,可以获得回弹后的弯曲角度,进而获得后续控制系统的神经网络预测模型的训练样本。
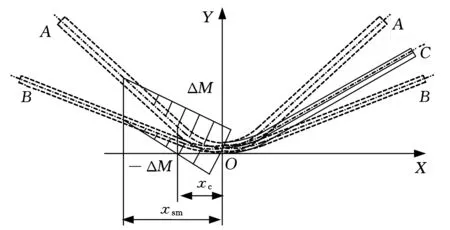
图3 拼焊板V形自由弯曲回弹分析
2 工艺参数对弯曲力的影响
根据所建的回弹解析模型,确定影响拼焊板弯曲回弹的因素,如表1所示。在每个因素下,选择3个水平值研究该因素对拼焊板V形弯曲的弯曲力和回弹后弯曲角的影响。在研究某一因素对弯曲力和回弹后弯曲角的影响规律时,其他因素选用表中“水平2”列值。
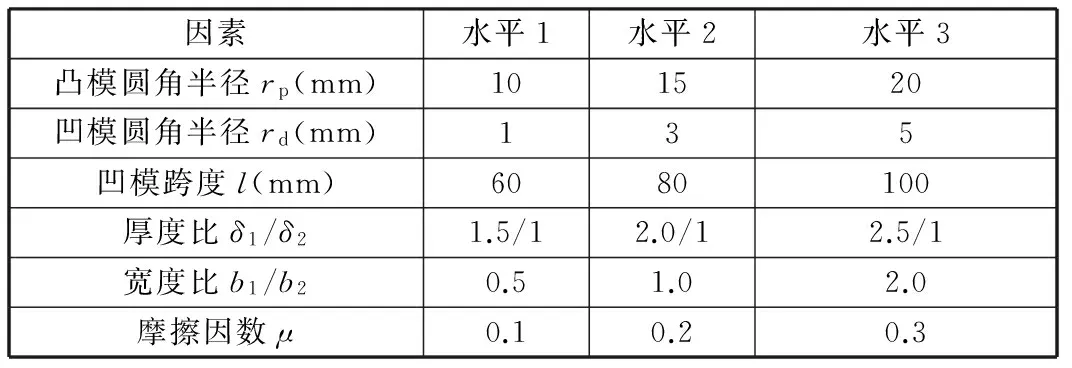
表1 试验因子及其水平
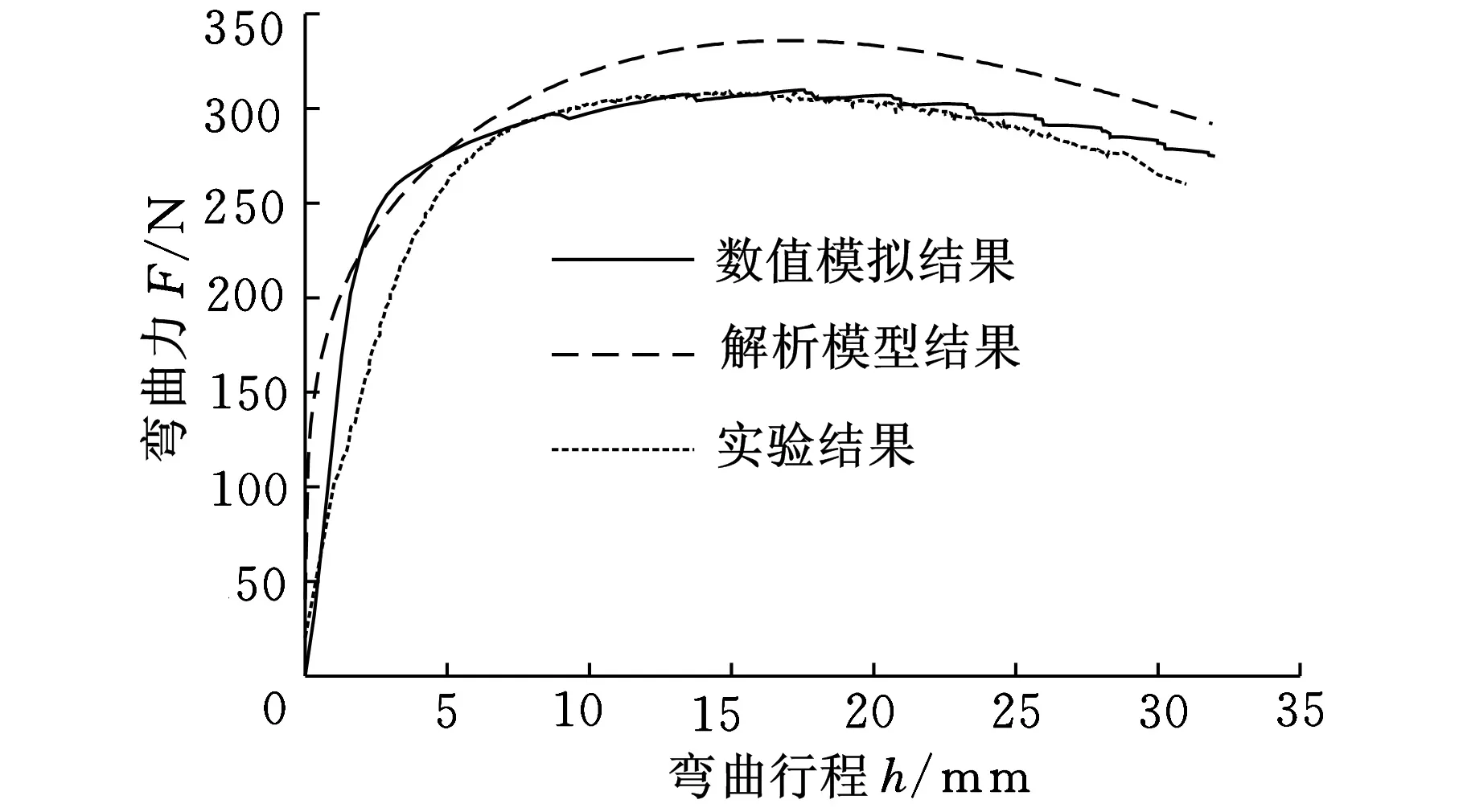
图4 弯曲力-弯曲行程对比曲线
在研究拼焊板V形自由弯曲各影响因素对弯曲力影响规律之前,需要验证解析模型的计算精度。实验材料选用ST12板,屈服强度σs=178.60 MPa,弹性模量E=196.26 GPa,强度系数K=493.62 MPa,硬化指数n=0.224,泊松比ν=0.3。拼焊板母板宽25 mm,拼焊板料厚比为2.0/1。模具的凸模圆角半径rp=10 mm,凹模圆角半径rd=1 mm,凹模跨距l=52.5 mm,数值模拟和理论计算中取摩擦因数μ=0.1。解析模型、数值模拟和实验所得结果如图4所示。从图4可以看出,数值模拟结果与实验结果较为接近,两者与解析模型结果存在一定偏差;屈服点附近,数值模拟与解析模型预测的弯曲力接近,而与实验结果差别较大,但3条曲线随行程的变化趋势一致,因此,可以应用上述解析模型分析拼焊板自由弯曲力的影响规律。
2.1凸模圆角半径对弯曲力的影响
分别取凸模圆角半径rp为10 mm、15 mm和20 mm,得出不同凸模圆角半径下弯曲力行程曲线,如图5所示。从图5可以看出,弯曲行程小于6 mm时,3种凸模圆角半径下的弯曲力基本相同;弯曲行程大于6 mm时,3种凸模圆角半径下的弯曲力差值逐渐增大;相同弯曲行程下,弯曲力随着凸模圆角半径的增大而增大。
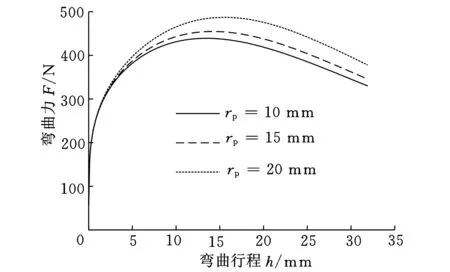
图5 凸模圆角半径对弯曲力的影响
2.2凹模圆角半径对弯曲力的影响
分别取凹模圆角半径rd为1 mm、3 mm和5 mm,得出不同凹模圆角半径下弯曲力行程曲线,如图6所示。从图6可以看出,弯曲行程小于5 mm时,3种凹模圆角半径下的弯曲力基本相同;弯曲行程大于5 mm时,3种凹模圆角半径下的弯曲力出现差别,但相差不大;相同弯曲行程下,凹模圆角半径大的弯曲力大。

图6 凹模圆角半径对弯曲力的影响
2.3凹模跨度对弯曲力的影响
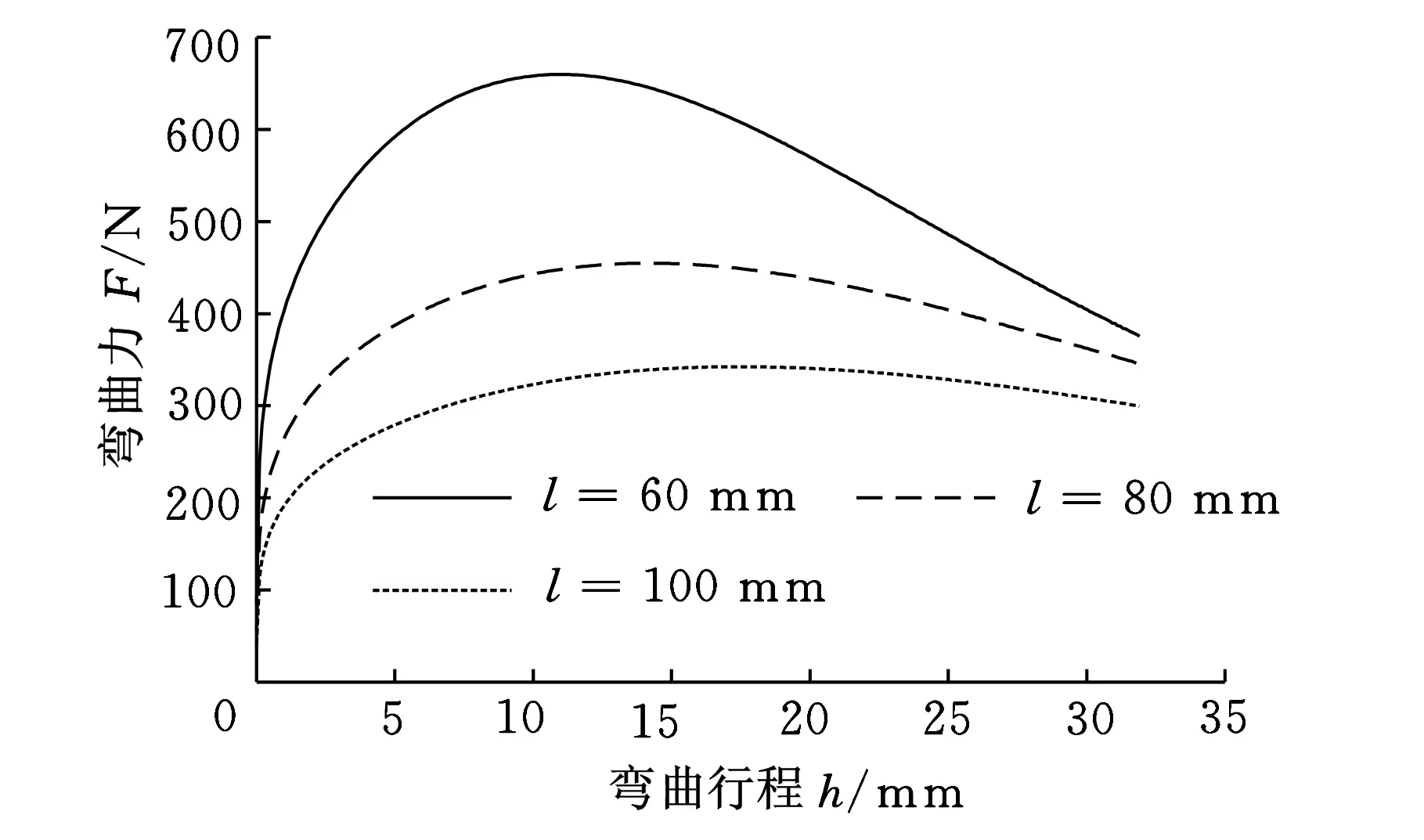
图7 凹模跨度对弯曲力的影响
分别取凹模跨度l为60 mm、80 mm和100 mm,得出不同凹模跨度下弯曲力行程曲线,如图7所示。从图7可以看出,相同弯曲行程下,3种凹模跨度的弯曲力差值较大;跨度为60 mm时的弯曲力最大,弯曲力变化梯度也较大。随着弯曲行程的增加,3种凹模跨度下弯曲力差值逐渐减小。
2.4厚度比对弯曲力的影响
分别取厚度比δ1/δ2为1.5/1、2.0/1和2.5/1,得出不同拼焊板厚度比下的弯曲力行程曲线,如图8所示。从图8可以看出,相同弯曲行程下,3种拼焊板厚度比的弯曲力差值较大;随着弯曲行程的增加,3种厚度比下的弯曲力差值有所减小。厚度比为2.5/1的拼焊板成形弯曲力最大。
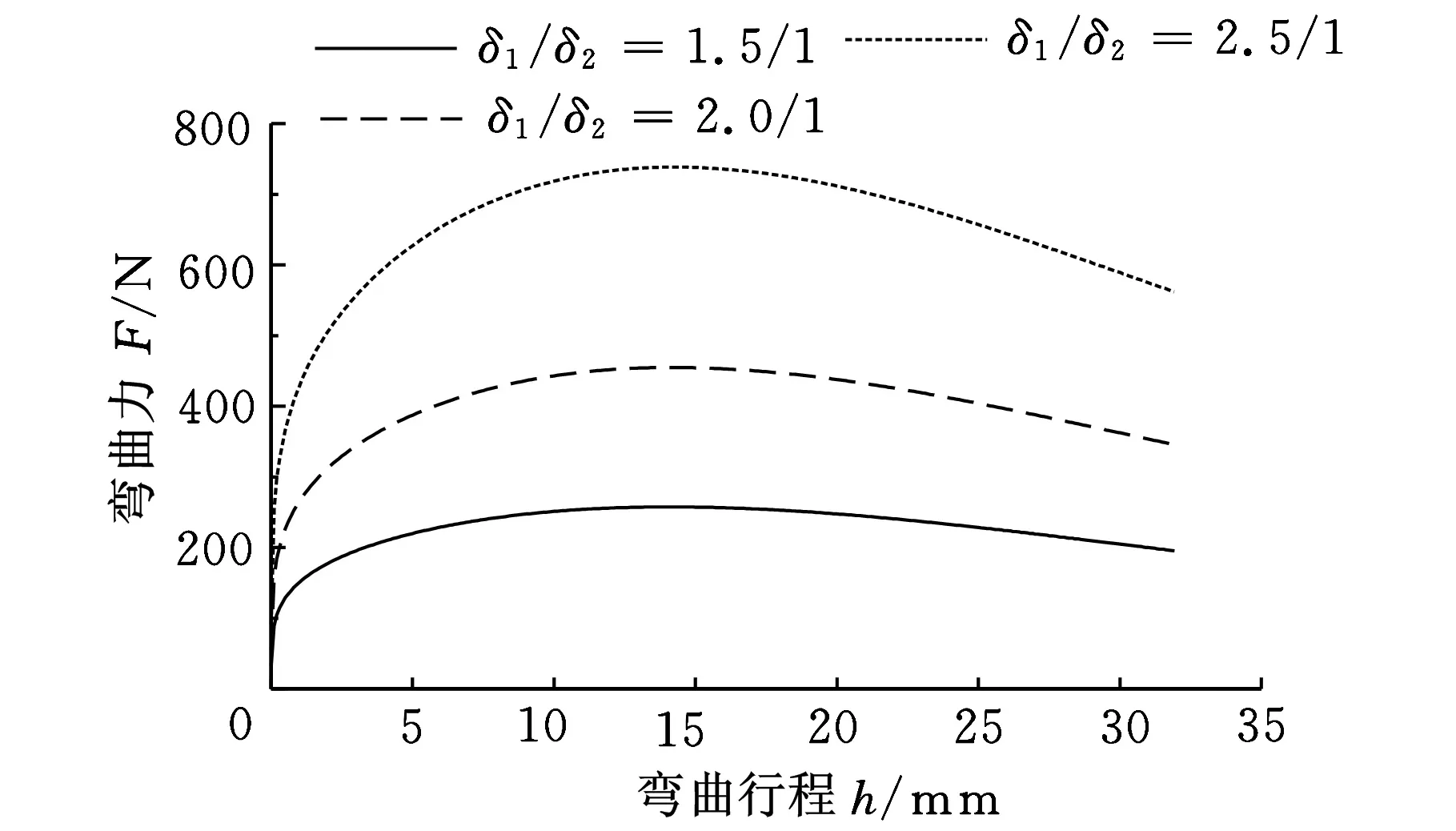
图8 厚度比对弯曲力的影响
2.5宽度比对弯曲力的影响
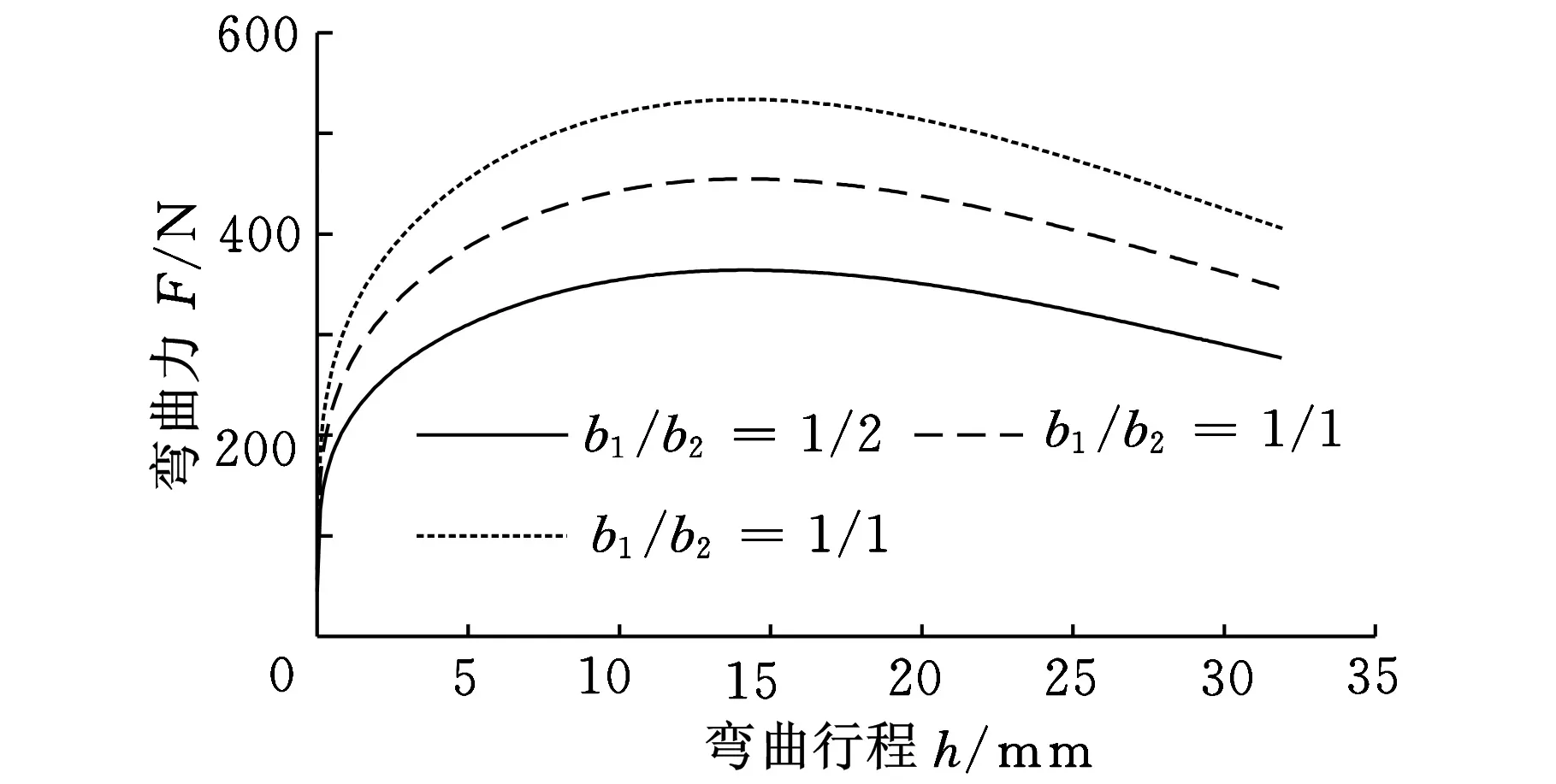
图9 宽度比对弯曲力的影响
分别取拼焊板宽度比b1/b2为1/2、1/1和2/1,得出不同拼焊板宽度比下弯曲力行程曲线,如图9所示。从图9可以看出,相同弯曲行程下,3种拼焊板宽度比的弯曲力差值较大;拼焊板宽度比为2/1时,弯曲力最大,而且3种拼焊板宽度比下的弯曲力变化梯度相当。随着弯曲行程的增加,3种拼焊板宽度比下的弯曲力差值有所减小。
2.6摩擦因数对弯曲力的影响
分别取摩擦因数μ为0.1、0.2和0.3,得出不同摩擦因数下弯曲力行程曲线,如图10所示。从图10可以看出,弯曲行程小于7 mm时,3种摩擦因数下的弯曲力差值不大;弯曲行程大于7 mm时,3种摩擦因数下的弯曲力差值增大;摩擦因数为0.3时,拼焊板成形弯曲力最大。
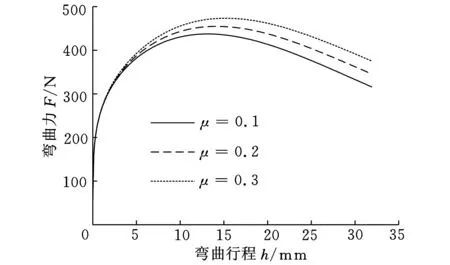
图10 摩擦因数对弯曲力的影响
3 工艺参数对回弹后弯曲角的影响
在液压机上完成拼焊板V形自由弯曲实验后,采用美国CimCore公司生产的3000i系列柔性三坐标测量系统对卸载后的弯曲角度进行点接触式检测。实验、数值模拟和解析模型的结果如图11所示,从图11可以看出,数值模拟和解析模型结果与实验结果都存在一定偏差,解析模型的最大相对误差为3.03%,但解析模型、数值模拟和实验结果曲线变化趋势一致。
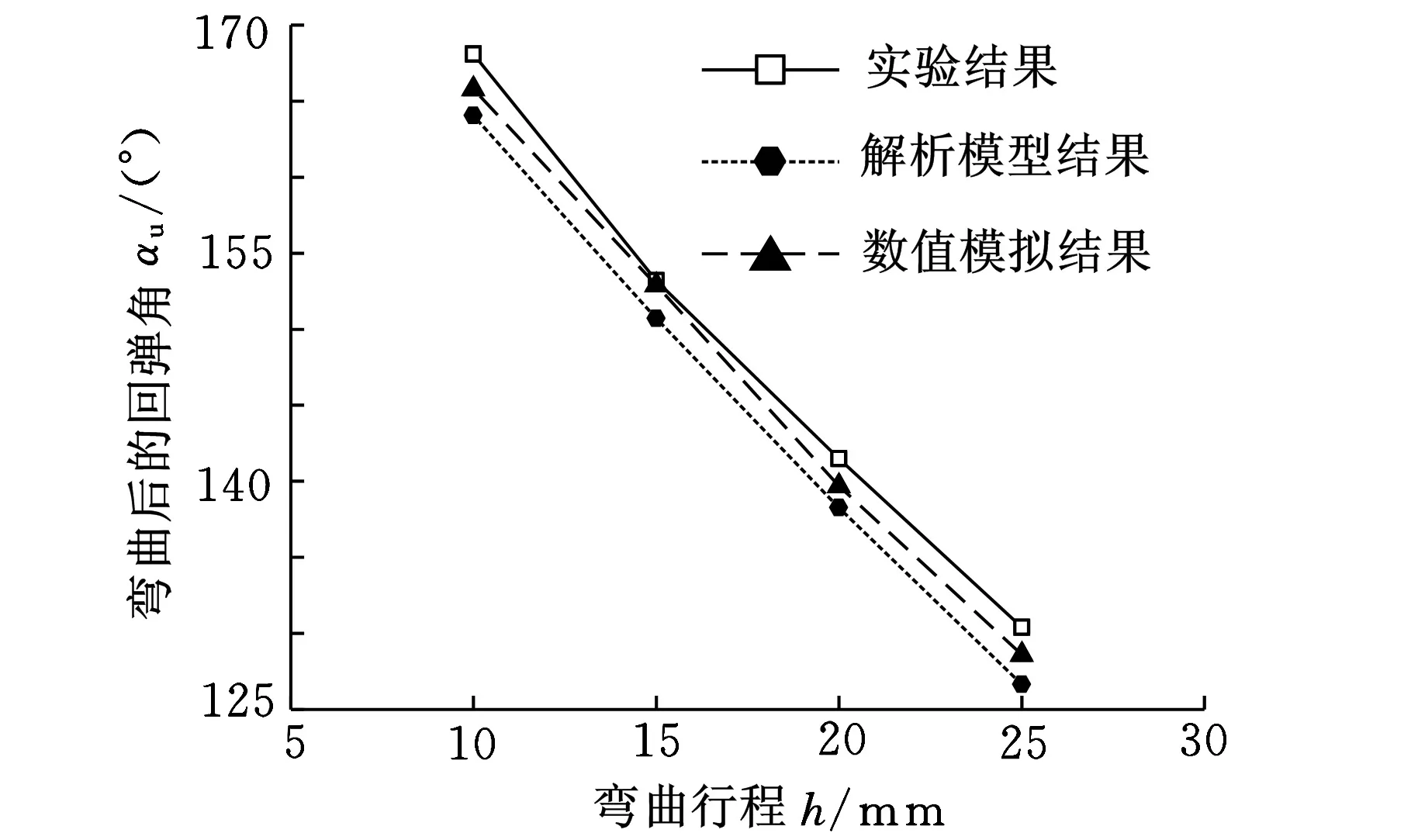
图11 卸载后弯曲角αu实验与理论对比曲线
3.1凸模圆角半径对回弹后弯曲角的影响
分别取凸模圆角半径为10 mm、15 mm和20 mm,得出不同凸模圆角半径下回弹后弯曲角行程曲线,如图12所示。从图12可以看出,弯曲行程较小时,3种凸模圆角半径下的回弹后弯曲角基本相同;随着弯曲行程的增加,3种凸模圆角半径下回弹后的弯曲角差值增大;凸模圆角半径越大,回弹后弯曲角越小。
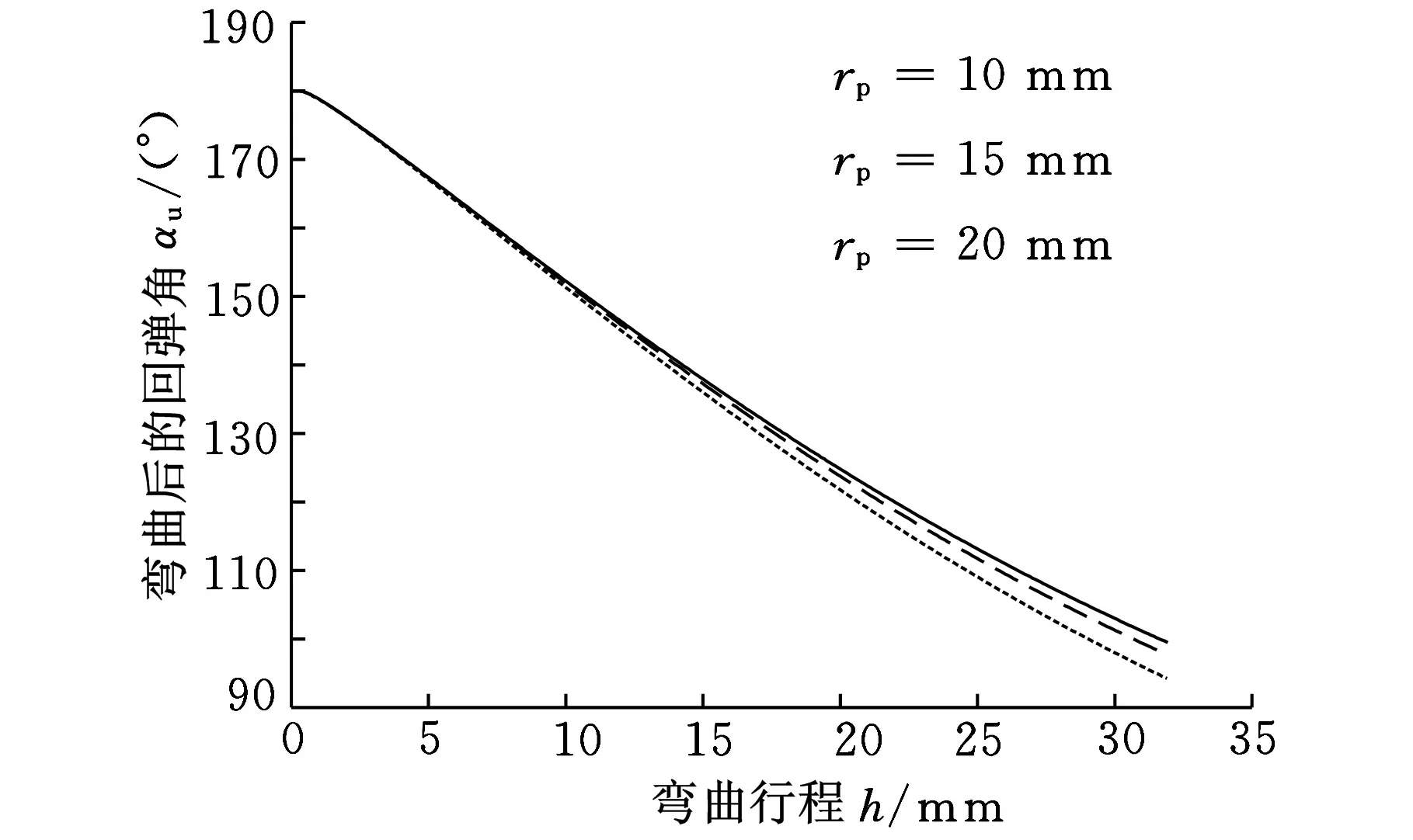
图12 凸模圆角半径对回弹后弯曲角的影响
3.2凹模圆角半径对回弹后弯曲角的影响
分别取凹模圆角半径为1 mm、3 mm和5 mm,得出不同凹模圆角半径下回弹后弯曲角行程曲线,如图13所示。从图13可以看出,随着凹模圆角半径的增大,回弹后弯曲角逐渐减小。
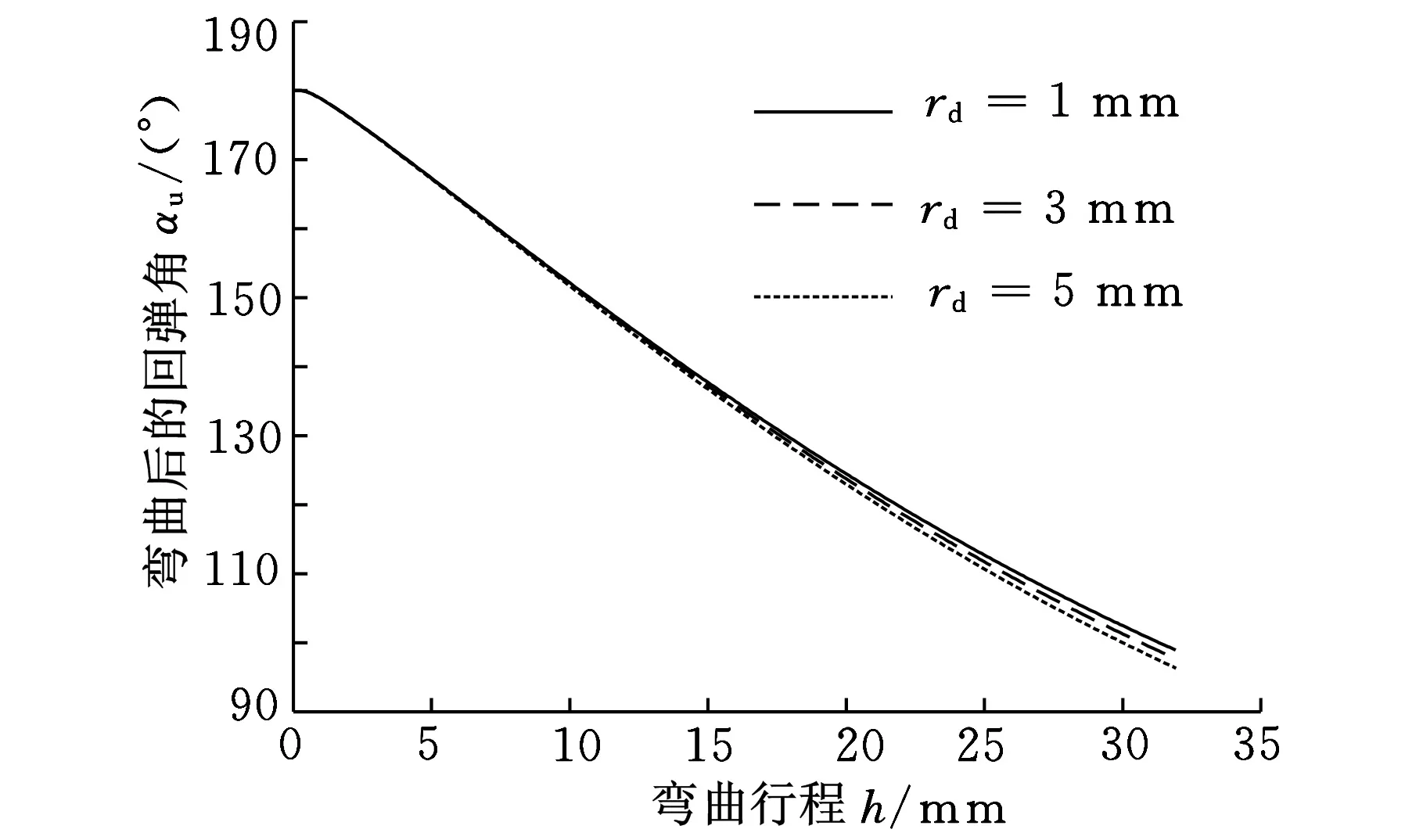
图13 凹模圆角半径对回弹后弯曲角的影响
3.3凹模跨度对回弹后弯曲角的影响
分别取凹模跨度为60 mm、80 mm和100 mm,得出不同凹模跨度下回弹后弯曲角行程曲线,如图14所示。从图14可以看出,3种凹模跨度下的回弹后弯曲角差值较大,跨度为60 mm时的回弹后弯曲角最小。跨度为60 mm时,回弹后的弯曲角随行程出现明显的非线性变化。随着弯曲行程的增加,3种凹模跨度下的回弹后的弯曲角差值增大。
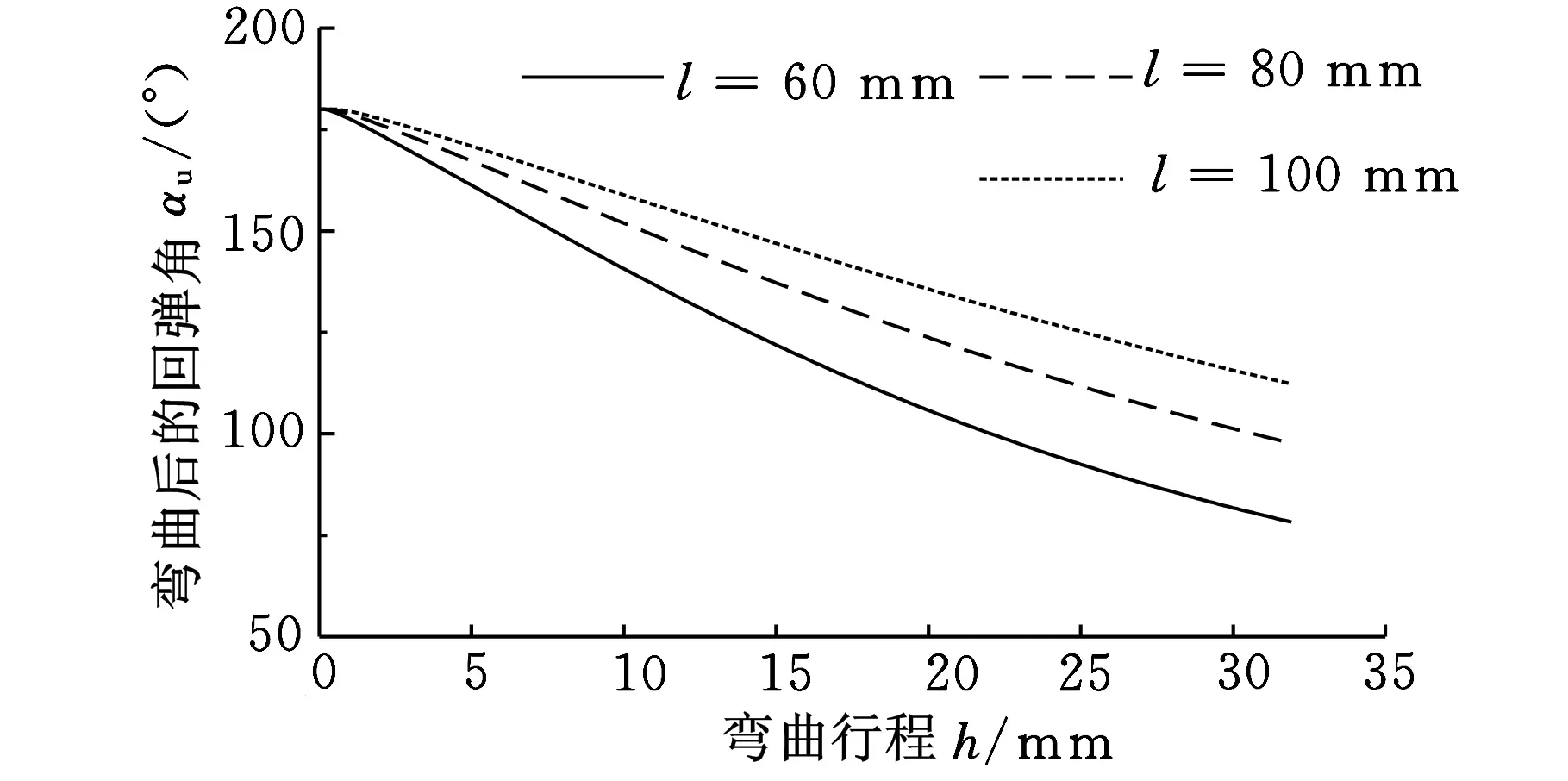
图14 凹模跨度对回弹后弯曲角的影响
3.4厚度比对回弹后弯曲角的影响
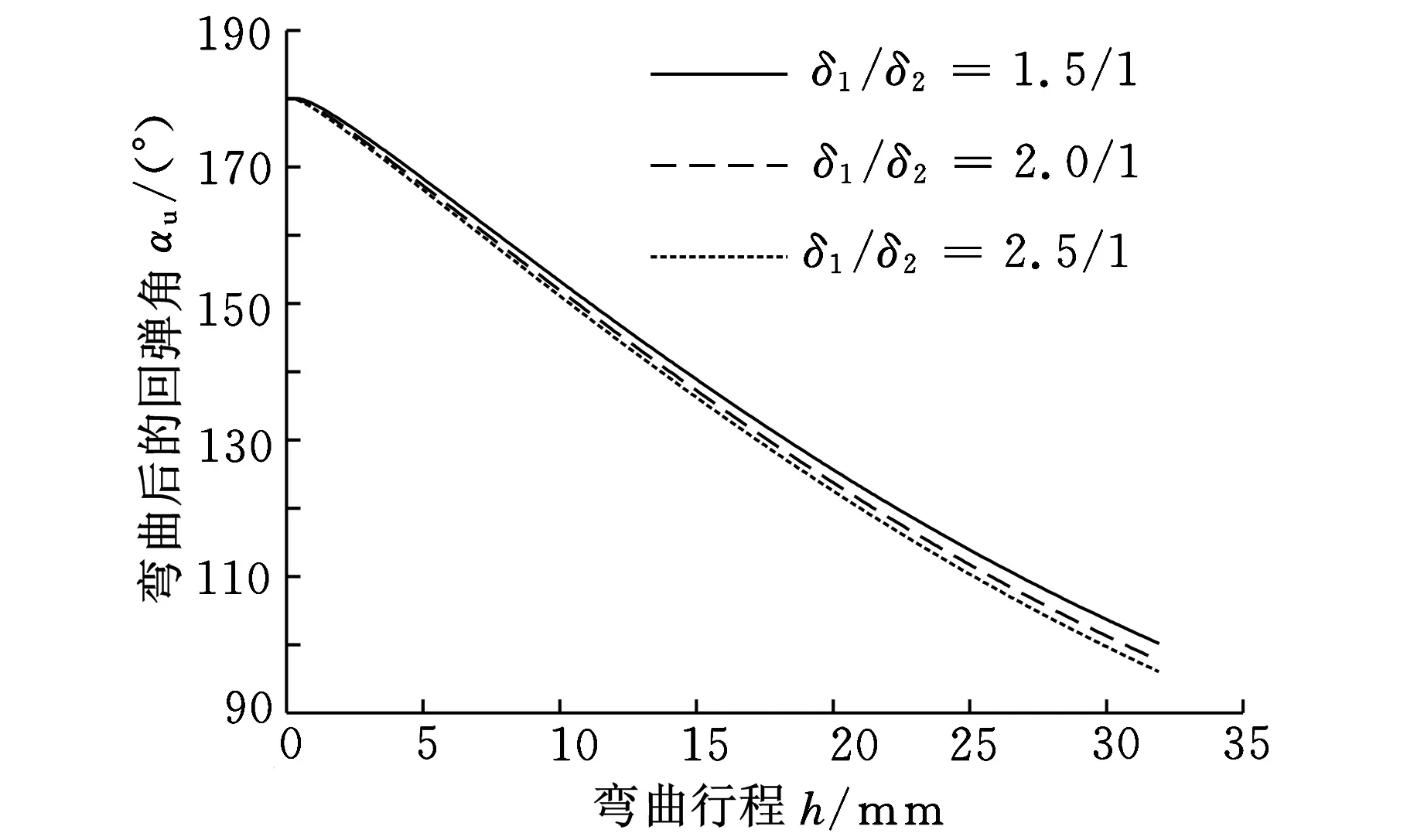
图15 厚度比对回弹后弯曲角的影响
分别取厚度比为1.5/1、2/1和2.5/1,得出不同厚度比下回弹后弯曲角行程曲线,如图15所示。从图15可以看出,随着弯曲行程的增加,3种厚度比下的回弹后弯曲角差值有所增大,厚度比为2.5/1的拼焊板回弹后弯曲角最小。
3.5宽度比对回弹后弯曲角的影响
分别取宽度比为1/2、1/1和2/1,得出不同拼焊板宽度比下的回弹后弯曲角行程曲线,如图16所示。从图16可以看出,3种拼焊板宽度比下的回弹后弯曲角基本相同,宽度比对回弹后弯曲角的影响较小。
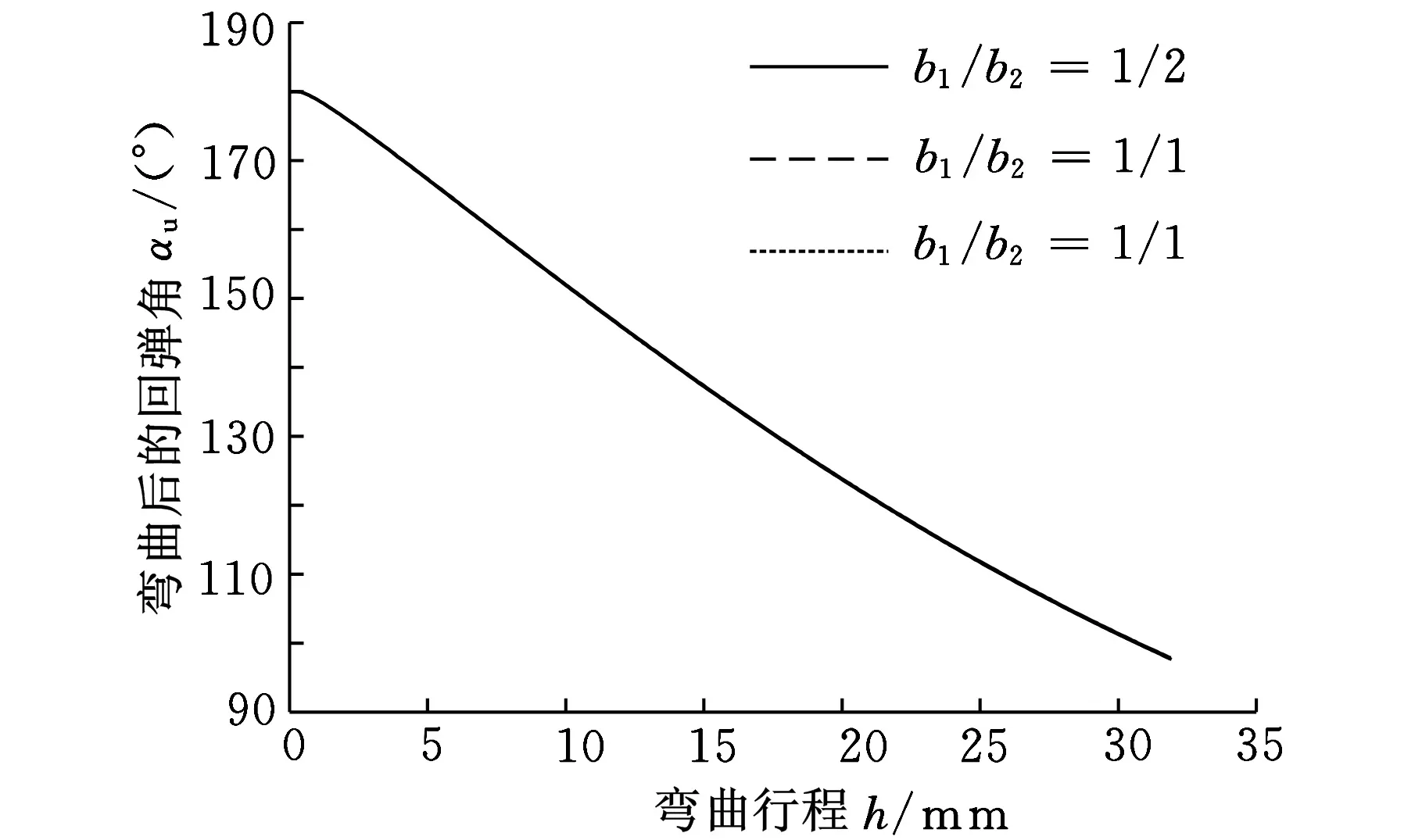
图16 宽度比对回弹后弯曲角的影响
3.6摩擦因数对回弹后弯曲角的影响
分别取摩擦因数为0.1、0.2和0.3,得出不同摩擦因数下的回弹后弯曲角行程曲线,如图17所示。从图17可以看出,3种摩擦因数下的回弹后弯曲角基本相同,摩擦因数对回弹后弯曲角的影响较小。
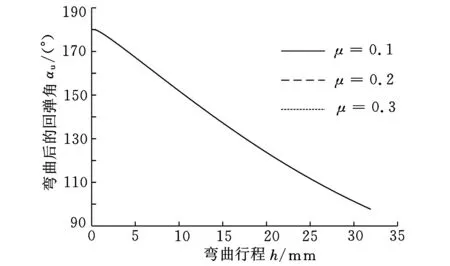
图17 摩擦因数对回弹后弯曲角的影响
4 弯曲回弹控制主要影响因素
拼焊板V形自由弯曲成形及回弹控制系统包含材料性能的识别模型和针对单一个体的特殊性进行相应工艺参数预测的模型。解析模型存在迭代计算,故利用解析法建立的工艺参数识别和预测模型,难以保证系统运行的实时性。神经网络模型可以实现多输入和多输出的映射关系,且算法效率高。利用上述解析模型构造样本集对神经网络进行训练和学习。神经网络模型确定输入输出变量后,需要一定数量的样本数据来训练神经网络,而样本数量的选取与神经网络的输入、输出和隐层节点数相关[5,10],即
KN=αNT
(20)
式中,K为输出节点个数;N为样本数;NT为待定网络参数个数;α为网络调节系数(一般取1~2)。
对于单隐层网络,待定网络参数的个数为[5,10]
NT=J(I+K)+J+K
(21)
式中,I为输入节点数;J为隐层节点数。
从式(20)、式(21)可以看出,输入、输出和隐层节点越多,网络规模越大,训练时间越长,因此,在建立回弹控制模型时,需要确定主要控制变量,减小神经网络规模,提高神经网络在线运行效率。在表1所示各影响水平范围内,根据解析模型得出了不同工艺参数对弯曲力和回弹后弯曲角的影响规律:凸模圆角半径、凹模跨度、厚度比和宽度比对拼焊板V形自由弯曲力影响较大,在建立材料性能识别模型时,应将上述因素作为输入变量;凸模圆角半径、凹模圆角半径、凹模跨度和厚度比对回弹后弯曲角影响较大,在工艺参数预测模型时,应将上述因素作为输入变量。
5 结论
(1)本文建立了可适用于拼焊板小曲率自由弯曲回弹的解析预测模型,所建立的回弹预测模型将成形过程分为贴模阶段和未贴模阶段进行研究。分别根据贴模态和未贴模态的拼焊板弯矩分布特点,构建了2种状态下的曲率分布方程。
(2)在自由弯曲成形阶段,基于行程加载得出了弯曲力和弯曲行程关系;在自由弯曲卸载阶段,考虑了两母板间相互作用的弯矩,基于单一母板求解了拼焊板母板回弹后的弯曲角。
(3)在表1所示水平范围内,根据解析模型得出了不同工艺参数对弯曲力和回弹后弯曲角的影响规律:凸模圆角半径、凹模跨度、厚度比和宽度比对拼焊板V形自由弯曲力影响较大,在建立材料性能识别模型时,应将上述因素作为输入变量考虑;凸模圆角半径、凹模圆角半径、凹模跨度和厚度比均对回弹后弯曲角影响较大,在工艺参数预测模型时,应将上述因素作为输入变量考虑。
[1]陈刚强,李光耀,孙光永,等.拼焊板车门焊缝布置与尺寸优化设计方法研究[J].中国机械工程,2013,24(1):103-109.
Chen Gangqiang,Li Guangyao,Sun Guangyong,et al.Research on Layout of Weld Lines and Size Optimization for TWB Doors[J].China Mechanical Engineering,2013,24(1):103-109.
[2]Chang S H,Shin J M,Heo Y,et al.Springback Characteristics of the Tailor-welded Strips in U-bending[J].Journal of Materials Processing Technology,2002,130/131:14-19.
[3]姜银方,丁新立,袁国定,等.差厚激光拼焊板的拉延切边回弹特性[J].机械工程学报,2008,44(12):203-207.
Jiang Yingfang,Ding Xinli,Yuan Guoding,et al.Investigation of Draw-trimming Springback of Laser Tailor-welded Blanks[J].Chinese Journal of Mechanical Engineering,2008,44(12):203-207.
[4]童正国,林建平,田浩彬,等.直线焊缝差厚拼焊板的成形规律[J].机械工程学报,2008,44(5):215-219.
Tong Zhengguo,Lin Jianping,Tian Haobin,et al.Formability Principles of Linear-weld-line Tailor-weld Blank(TWBs) with Different Thickness Ratios[J].Chinese Journal of Mechanical Engineering,2008,44(5):215-219.
[5]官英平,赵军,苏春建. 宽板V形自由弯曲智能化控制过程材料参数识别及最优工艺参数预测术[J]. 机械工程学报,2005,41(4):199-202.
Guan Yingping,Zhao Jun,Su Chunjian.Material Parameter Identification and Optimal Technological Parameter Prediction for Intelligent Control of V Shape Free Bending Process of Wide Sheet Metal[J]. Chinese Journal of Mechanical Engineering,2005,41(4):199-202.
[6]余同希,章亮炽. 塑性弯曲理论及其应用[M]. 北京:科学出版社,1992.
[7]Kazan R,Firat M,Tiryaki A E.Prediction of Springback in Wipe-bending Process of Sheet Metal Using Neural Network[J]. Materials and Design, 2009,30(2):418-423.
[8]姜银方,袁国定,杨继昌. 拼焊板弯曲回弹的理论与试验研究[J]. 机械工程学报,2005,41(12):200-204.
Jiang Yinfang,Yuan Guoding,Yang Jichang.Springback in the Bending of Tailor Welded Blanks in Theory and Experiment[J].Chinese Journal of Mechanical Engineering,2005,41(12):200-204.
[9]段永川,官英平,赵军. 拼焊板宽板V形自由弯曲回弹预测及试验验证[J]. 机械工程学报,2012,48(20):63-69.
Duan Yongchuan,Guan Yingping,Zhao Jun. Prediction and Experiment Verification of Spring-back of Tailor Welded Blanks Air Bending Process[J].Journal of Mechanical Engineering,2012,48(20):63-69.
[10]闻新.MATLAB神经网络应用设计[M].北京:科学出版社,2000.
(编辑张洋)
Analysis of Effect Factor of Springback Control of Tailor Welded Blanks Air Bending Process
Duan YongchuanGuan Yingping
Key Laboratory of Advanced Forging & Stamping Technology and Science Ministry of Education,Yanshan University,Qinhuangdao,Hebei,066004
An analytical springback prediction model of TWBs for air bending process was put forward for small curvature bending.At the air bending unloading phase,the interaction moment of the two parent blanks was introduced to the model,the unloaded angle was obtained based on a single parent plate in the analytical model.The effect law of bending force and unloaded angle were obtained using analytical model.The main effect factors of bending force and unloaded angle were determined.
tailor welded blank(TWB);air bending;springback control;analytical model;effect factor
2013-09-09
国家自然科学基金资助项目(51275444);高等学校博士学科点专项科研基金资助项目(20121333110003);秦皇岛市科技支撑计划资助项目(201401A034);燕山大学博士基金资助项目(B861)
TG386.31DOI:10.3969/j.issn.1004-132X.2015.02.024
段永川,男,1983年生。燕山大学机械工程学院讲师。主要研究方向为拼焊板冲压成形。发表论文7篇。官英平(通信作者),男,1963年生。燕山大学机械工程学院教授、博士研究生导师。

