周期结构表面散射系数测试及修正方法*

曾向阳　杜博凯　王海涛

（西北工业大学航海学院　西安　710072）

周期结构表面散射系数测试及修正方法*

曾向阳†杜博凯王海涛

（西北工业大学航海学院西安710072）

无规入射散射系数是描述结构声反射特性的重要参数，在周期结构等典型扩散体的声学设计和室内声场模拟中具有重要的作用。本文给出了混响室法测试无规入射散射系数的原理，对半圆型周期结构进行了实验测试，并针对测试中存在的缺陷，提出了一种考虑空气间隙吸声的修正方法，经验证具有较好的修正效果。

周期结构，散射系数，测量方法，空气间隙

1　引言

界面声散射是指由于几何反射和波动衍射而产生的声波在界面入射点向镜面反射方向以外其他方向传播的现象。散射系数是描述结构表面散射性能的关键参数。在各种散射体中，周期结构是一种特殊的界面散射结构，而且应用广泛。

近年来，对于周期结构散射系数的研究越来越多，现有主要方法是实验测量和数值计算。其中，数值计算通常采用基于波动声学理论的方法，包括：Ripoll等提出的KA方法［1］、Kosaka［2］、张建军等［3］提出的边界元法（BEM）；王海涛等［4-5］提出的边界型无网格数值计算模型（Boundary meshless model，BMM）和无网格平面波分解模型（Meshless plane wave decomposition model，MPWD）。这些方法尤其适用于在设计阶段对周期结构散射系数进行预计和分析。

实验测量是另一种获取散射系数的重要途径。2004年，相关的国际标准被提出［6］。不过，由于测试过程比较复杂，从测试原理到测试流程都还存在一些不够完善的地方。例如，对于脉冲响应获取这个关键问题，同步脉冲响应的数量、不同脉冲响应中散射成分之间的相干等因素都会对其精度造成影响。莫方朔等［7］对这方面的问题进行了理论分析，并在不同脉冲响应中散射成分存在相关时，研究了利用T10或T20估计早期衰减速率产生的误差。此外，试件边缘衍射作用、测试装置和测试仪器也会带来一定的误差。

本文以半圆型周期结构为对象，研究了其散射系数测试方法，并针对试件与转台之间的空气间隙吸声导致的测量误差问题，提出了相应的修正方法，并以无网格数值计算结果作为参考，对修正前后的散射系数进行对比，分析修正方法的有效性。

2　无规入射散射系数测试原理

如图1所示，无规入射的声波在界面发生反射，反射能量由镜面反射和散射组成。ISO将无规入射声散射系数s定义为：1减去扩散声场中散射界面上镜面反射声能量后与总反射声能量的比值。因此，散射系数可表示为［8］

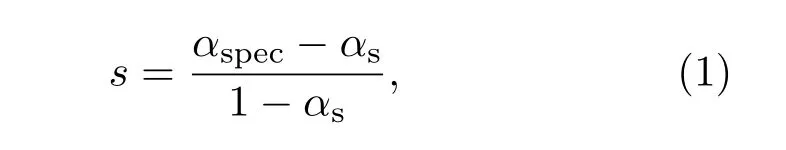
其中αs为界面的无规入射吸声系数，即入射声能减去扩散声场中表面总反射声能之后与入射声能的比值，可由混响室法测得；αspec是无规入射镜面吸声系数（入射声能减去扩散声场中表面上镜面反射声之后与入射声能的比值），即1减去镜面反射声能后与入射声能比值。可见，要测试散射系数，关键是测量无规入射镜面吸声系数αspec，以下对其测量原理加以阐述。

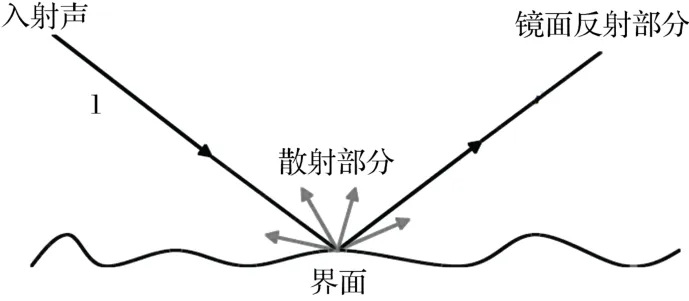
图1　声波在界面处的散射Fig.1 Sound scattering at the interface

图2给出了自由场中从试件不同方位凹凸表面反射引起的3个带通脉冲响应。显然，三者的早期反射部分是高度相关的，被认为是镜面反射分量，而后期部分相位不同且取决于特定方位，反射脉冲的“尾部”能量包括了散射分量。为了从反射脉冲中提取镜面反射能量，可以通过不同试件方位获得的脉冲响应做同步平均得到。

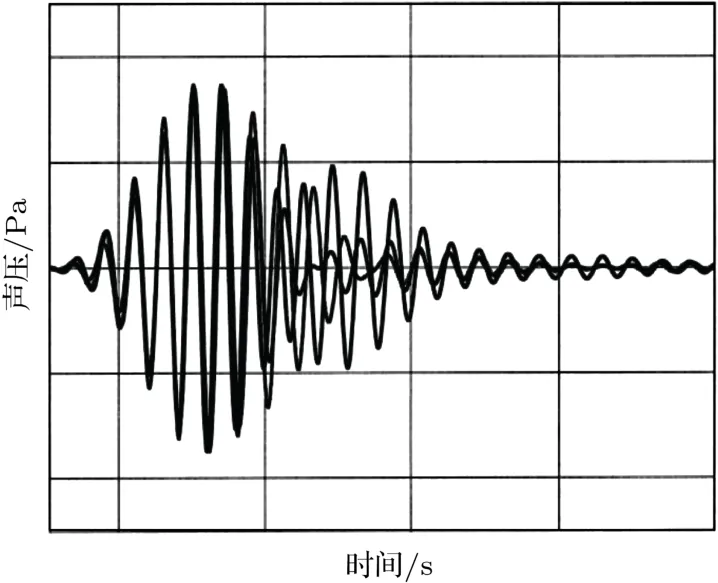
图2　不同位置测得的脉冲响应Fig.2 Three impulse responses measured at the different positions

实验中，将试件置于匀速旋转的转台上，多次测量不同位置处的脉冲响应。由于声源和传声器的位置是固定的，脉冲响应的镜面反射声成分是完全相关的，而散射声成分被假定为不相关，叠加后的能量衰减曲线可以表示为［8］

式（2）中，Tsp是相当于混响室法测量吸声系数时，声场中有吸声系数为αspec试件时的混响时间；Ts为试件的无规入射吸声系数为αs时的混响时间。N表示一个测量周期（即试件旋转一周所用的时间）内测得的脉冲响应的个数。由于Tsp与Ts在数量级上相当，在N取值足够大时，E（t）的后一个指数项相对于前一个指数项非常小，可以忽略，这时不相关的散射成分就近似抵消了。

于是，利用混响室测量吸声系数的方法可以获得αspec。这里仅给出无规入射吸声系数和镜面吸声系数的计算公式。

无规入射吸声系数：

式（3）～（4）中，T1表示在不放置试件、转台也不旋转情况下测得的混响时间，T2、T3、T4分别表示“不旋转、有试件”、“旋转、无试件”和“旋转、有试件”三种情况下测得的混响时间。V表示混响室体积，S表示试件的面积，c表示声速，m表示周围环境对测量的影响因素，当两次测量时间间隔较小时可以不考虑其影响。

3　无规入射散射系数测试实验

实验样品为自制半圆型周期结构，共7个周期，形状为圆形，半径r=0.5 m，每个周期长度l=0.075 m，高度h=0.0375 m，试件面积S=0.785 m2。在5.72 m×3.16 m×4.8 m的西北工业大学航海学院混响室中进行测量，采用球形声源作为激励，利用Dirac软件作为主测系统。实验现场如图3所示。

图3　实验现场Fig.3 Experiment site

每种情况下的测量都随机选择3种声源和传声器的位置，最终得到6个混响时间。进行算术平均获得对应情况下有效的混响时间，以减小随机误差。

转台静止时，根据底板上有、无试件分别得到两组脉冲响应，由此计算得到混响时间T1和T2，再由式（3）计算得到无规入射吸声系数。在转台旋转时，同理可得T3，T4，由式（4）可算得镜面吸声系数。再按照式（1）计算得到散射系数。各个频率处的结果如图4所示。

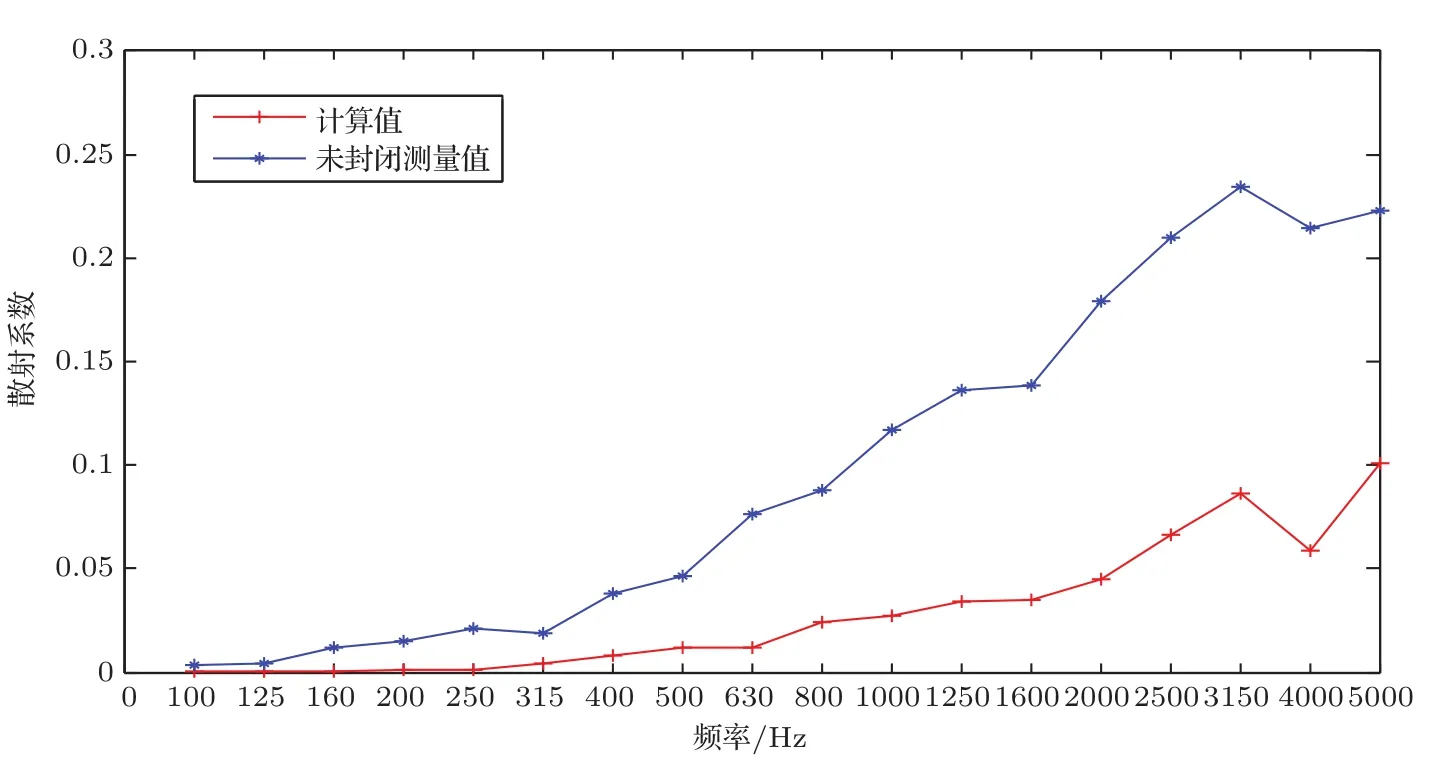
图4　测量值与计算值的比较Fig.4 Comparison of the measured and calculated results

为分析测量结果的有效性，选取自编边界型无网格数值计算程序所得的结果作为参考值（该数值方法的正确性已在文献［4-5］中证明）。对比情况如图4所示。从图4中可以看出，在所有频段，测量值相比于计算值均明显偏大。分析原因，与被测试件与底板的缝隙具有的吸声作用有关，前述测量中，该吸声作用被作为试件吸声系数的一部分，这导致按照混响室法测得的试件吸声系数比实际值偏大，因而按照公式（1）可知，最后所得的散射系数也相应增大。下文针对这一问题提出修正方法。

4　无规入射散射系数测试方法的修正

4.1间隙吸声系数计算方法

为了修正间隙吸声对散射系数测量的影响，首先需要对间隙吸声系数进行估算。这里根据声线与间隙各个表面的碰撞次数来决定其在总吸声中的贡献。首先将射入间隙的声线速度分解成两个方向：沿间隙深度方向v1和垂直于间隙深度方向v2。利用v1计算出声线在间隙内的运动时间t，再结合v2就能计算出声线在间隙平面内的运动路程s。碰撞次数N可以根据s和封闭平面内声线的平均自由程为确定。再按照面积比例可以分别得到声线与地板及试件内表面的碰撞次数N1和N2，结合对应的吸声系数α1和α2即可计算出每条声线在间隙内的声能损失，最后通过积分可得间隙的等效吸声系数α。详细推导过程如下：

如图5所示，声线以速度v由空气间隙左端平面随机射入间隙之中（为简化计算，将间隙简化为一个等腰三角形）。

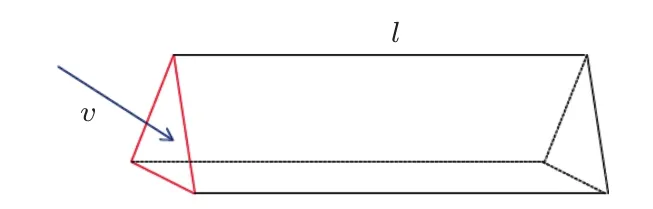
图5　间隙声入射示意图Fig.5 Incidence of the sound at the gap

首先计算平均自由程。如图6所示，假设一根声线以速度v在一个长和宽分别为l1和l2的矩形内运动。

图6　计算平均自由程Fig.6 Calculation of mean free path

声线每秒内与长和宽的碰撞次数分别为vsinθ/l2和v cosθ/l1。

假设每秒发射的声线数为2πn，n为单位角内的声线数，则每秒碰撞次数：

如图7所示，声线进入间隙时，声速v分解为v1和v2。假设等腰三角形间隙深度为lh，边长分别为a、b、c，其中a=b。设声速的方向与平面的夹角为θ，底板的吸声系数与试件内表面吸声系数分别为α1和α2。则声线在间隙内的运动时间t可以由声线沿着lh的方向的速度计算得到

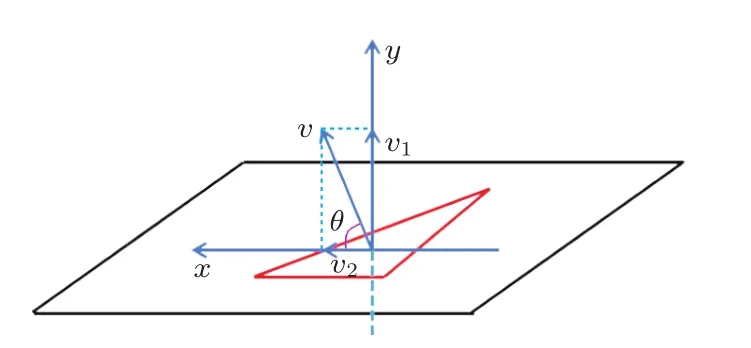
图7　声速的分解Fig.7 Decomposition of sound speed

声线与地板和试件内表面的碰撞次数可以按面积比例分配，这样声线与底板的碰撞次数N1为这样，间隙的总吸声系数可以表示为

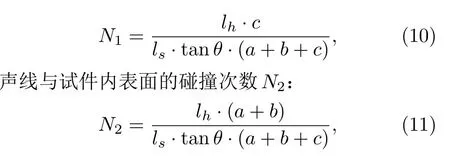
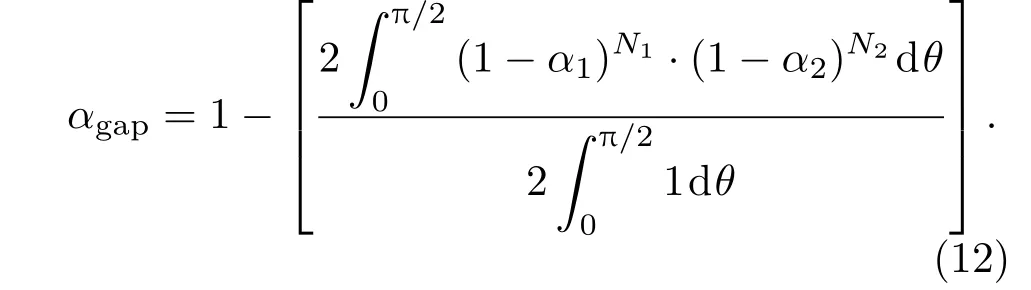
假设某频率处底板吸声系数分别为0.5和0.2，计算间隙等效吸声系数随试件内表面吸声系数的变化情况，结果见表1和表2。可以看出，间隙吸声系数总体较大，且受底板吸声系数和试件吸声系数的影响很大。也不难看出，各种情况下的间隙吸声系数均高于试件吸声系数，这也证明了直接测量方法将间隙吸声计入试件吸声是产生误差的一个原因。4.2散射系数修正方法

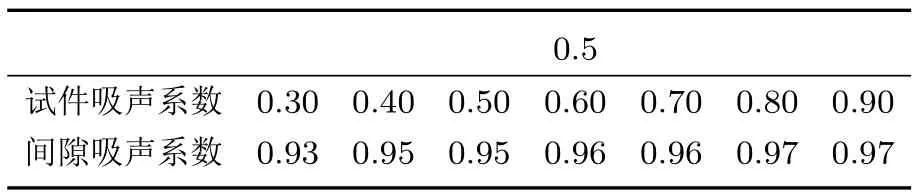
表1　底板吸声系数为0.5时的间隙吸声系数Table 1Absorption coefficient of the air gap（when absorption coefficient of the baseboard is 0.5）

表2　底板吸声系数为0.2时的间隙吸声系数Table 2Absorption coefficient of the air gap（when absorption coefficient of the baseboard is 0.2）

假设每个空气间隙面积相同，则根据Sabine公式可知，在试件未被放置在转台上之前混响时间为

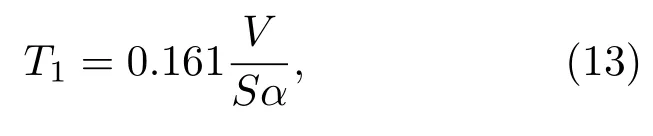
式（13）中，Sα涵盖了在未放置试件之前所有的吸声因素。

当试件被放置在转台上时，将空气间隙因素考虑进去之后，所得的混响时间为

其中Ssample和αsample为试件的表面积和吸声系数；Sgap是空气间隙表面积，αgap为空气间隙的吸声系数。

在单独考虑了空气间隙吸声之后，由式（13）、式（14）可得试件的吸声系数：

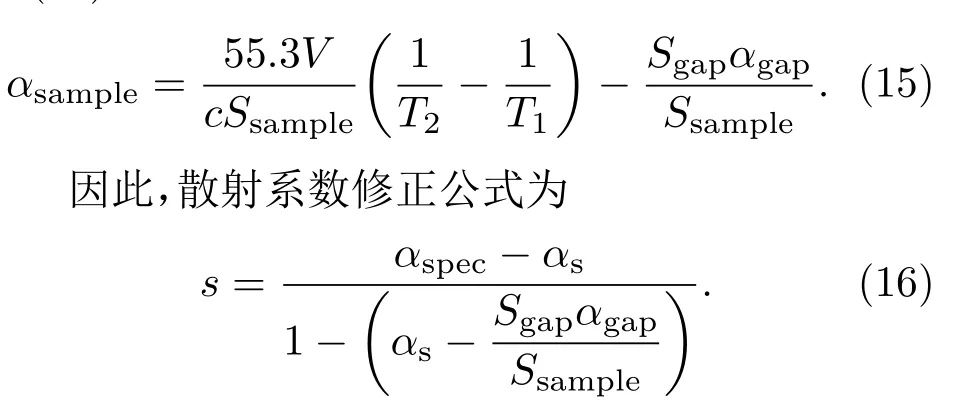
本实验中，底板、试件内外表面吸声系数（内外表面材料相同，吸声系数相同）的吸声系数见表3。

为了证明修正方法的有效性，将间隙用表面光滑的铁片封闭（如图8）后进行测量，以便对比。将测量所得的数据代入修正公式，并将未修正的测量值、间隙封闭后的测量值、修正值以及计算值进行比较，结果如图9所示。

图8　密封的间隙Fig.8 The sealed gap

表3　底板与试件内表面的吸声系数Table 3 Absorption coefficient of the internal surface of the sample and the baseboard

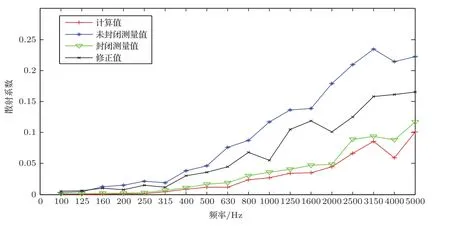
图9　修正方法的验证Fig.9 Validation of the correction method

可以看出，在低频段，四种情况的结果非常接近；在高频段，修正后的散射系数相比于未修正值均有所减小，并更接近计算值和间隙封闭后的测量值。这表明，通过估算间隙吸声有助于提高测量精度，也说明本文提出的修正方法是有效的。

5　结论

本文介绍了周期结构无规入射散射系数及其测量原理，并利用自制的试件和实验系统，按照标准方法完成了测量，然后针对测量方法中存在的空气间隙吸声问题提出了修正方法，并对比数值计算结果、空气间隙存在以及被完全被封闭几种情况下的结果，对修正方法进行了检验，证明修正方法能有效提高测量精度。由于无规入射散射系数测量方法提出的时间还不长，还存在其他一些影响测量精度的问题，后面将进一步开展这方面的研究工作。

［1］RIPOLL J，NTZIACHRISTOS V，CARMINATI R，et al. Kirchhoff approximation for diffusive waves［J］.Physical Review E，2001，64（5）：051917.

［2］张建军，曾向阳，王海涛.周期结构散射系数的边界元算法［J］.声学技术，2011，35（5）：104-106.

ZHANG Jianjun，ZENG Xiangyang，WANG Haitao. Boundary element algorithm for the calculation of scattering coefficients of periodic structures［J］.Technology Acoustics，2011，35（5）：104-106.

［3］KOSAKA Y，SAKUMA T.Numerical examination on scattering coefficients of architectural surfaces using the boundary element method［J］.Acoustical Science and Technology，2005，26（2）：136-145.

［4］王海涛，曾向阳.周期结构声散射系数的无网格数值计算方法［J］.计算物理，2013，30（2）：229-236.

WANG Haitao，ZENG Xiangyang.Meshless models for numerical calculation of scattering coefficients of periodic structures［J］.Chinese Journal of Computational Physics，2013，30（2）：229-236.

［5］WANG Haitao，ZENG Xiangyang.Calculation of sound fields in small enclosures using a meshless model［J］.Applied Acoustics，2013，74（3）：459-466.

［6］ISO17497-1：2004.Acoustics-sound-scatteing properties of surface-Part1：Measurement of the random-incidence scattering coefficient in a reverberation room［S］.

［7］莫方朔，盛胜我.无规入射散射系数测量中的声能衰减分析［J］.同济大学学报，2005，33（3）：404-408.

MO Fangshuo，SHENG Shengwo.Analysis of sound energy decay in measurement of random-incidence scattering coefficient［J］.Journal of Tongji University，2005，33（3）：404-408.

［8］VORLANDER M，MOMMERTZ E.Definition and measurement of random-incidence scattering coefficient［J］. Applied Acoustics，2000，60（2）：187-199.

Measurement and correction method for the surface scattering coefficient of a periodic structure

ZENG XiangyangDU BokaiWANG Haitao
（School of Marine Science and Technology，Northwestern Polytechnical University，Xi'an 710072，China）

Random-incidence scattering coefficient is an important parameter to describe the property of sound reflection on the surface of a structure.This coefficient shows its great importance in the acoustic design of typical diffuser such as periodic structure and the indoor sound field imitation.This paper presents the measurement theory of the random-incidence scattering coefficient by the reverberation chamber method. And the coefficient of a sine periodic structure was measured.Considering the defect of the measurement，a correction method was proposed and it is demonstrated to be effective.

Periodic structure，Scattering coefficient，Measuring method，Air gap

O422.5

A

1000-310X（2015）05-0433-06

10.11684/j.issn.1000-310X.2015.05.008

2015-01-04收稿；2015-06-24定稿

*国家自然科学基金项目（11374241）

曾向阳（1974-），男，湖北人，教授，研究方向：室内声学，声信号处理。†

E-mail：zenggxy@nwpu.edu.cn