稳健宽带波束形成器设计的低阶统计量法*

任维怡　陈华伟　鲍　彧

（南京航空航天大学电子信息工程学院　南京　210016）

稳健宽带波束形成器设计的低阶统计量法*

任维怡陈华伟†鲍彧

（南京航空航天大学电子信息工程学院南京210016）

由于传声器阵列通常对阵元失配误差较为敏感，因此稳健波束形成器的设计已成为传声器阵列处理领域的研究热点之一。概率密度法是目前传声器阵列稳健波束形成器设计中的一类重要方法，但该方法所需的阵元失配误差的概率密度信息在实际中较难获取。针对这一问题，本文研究了基于阵元失配误差低阶统计量的稳健波束形成器设计方法，该方法仅利用在实际中较易获取的阵元失配误差的一阶和二阶统计量信息。本文分别研究了基于阵元失配误差低阶统计量的固定权和变加权最小二乘波束形成器设计，给出了两种波束形成器的相关设计理论。理论和仿真分析表明，在小误差条件下，低阶统计量法所设计的波束形成器仍保持与概率密度法相当的性能。

宽带波束形成，传声器阵列，稳健性

1　引言

波束形成是阵列信号处理领域的关键技术之一，广泛应用于雷达、声呐、无线通信、地质勘探、医学成像、射电天文学等多个领域［1-3］。传声器阵列波束形成源于阵列天线波束形成的思想，改变了传统的单传声器处理模式。传统的单传声器处理模式仅在时频域对声信号进行处理，而传声器阵列还可在空域对声信号进行处理，实现时域-频域-空域联合处理。因此传声器阵列波束形成可以获得更好的性能，成为近年来音频和语音信号处理领域的研究热点之一。

传声器阵列波束形成器本质上可以看作空域滤波器。根据所处理信号频带宽度的不同，波束形成器可分为窄带和宽带波束形成器两大类。对于音频和语音等宽带信号，在实际中需要采用宽带波束形成器进行处理［4］，因而传声器阵列波束形成大多采用宽带波束形成器。经典的宽带波束形成器设计方法包括频域和时域实现方法等，这些方法设计出的波束形成器在理想情况下均能获得较好的性能。然而，当传声器阵元存在失配误差时，如传声器的增益、相位和位置误差，使用这些经典方法设计出的波束形成器的性能会显著下降，尤其对于小型传声器阵列［5-6］。因此设计出稳健的宽带波束形成器在实际应用中具有重要意义。

已有的稳健波束形成器设计方法有白噪声增益约束法、概率密度法等。白噪声增益约束法需要设置门限值对白噪声增益进行约束，但如何根据给定的传声器失配误差选取合理的门限值是该方法存在的一个难点。为此，文献［7］提出了概率密度法，根据阵元的失配误差概率密度函数信息进行稳健波束形成器设计，从而避免了白噪声增益约束法中门限值选取的难题。在该思想的基础上，近年来许多研究者又进一步发展了该方法［7-12］。虽然概率密度法有效解决了宽带波束形成器的稳健设计问题，但在实际应用中，传声器阵元失配误差的概率密度函数较难获取，一定程度上影响了该方法的实用性。针对这一问题，本文研究了基于阵元失配误差低阶统计量的方法，仅利用实际中较易获取的阵元失配误差的一阶和二阶统计量信息。我们分别研究了基于阵元失配误差低阶统计量的固定权和变加权最小二乘宽带波束形成器的设计，给出了这两类波束形成器的设计理论。理论分析和仿真结果表明，在小误差条件下，虽然低阶统计量法只利用了失配误差的低阶统计量信息，但所设计的波束形成器仍保持与概率密度法相当的性能。

2　研究背景

2.1阵列数学模型

考虑如图1所示的滤波求和时域宽带波束形成器结构，传声器阵列为M个传声器组成的均匀线阵列，阵元为具有平坦频率响应1的全向传声器，后接的有限冲激响应（Finite impulse response，FIR）滤波器的抽头数为L，采样频率为fs。当声源信号s（ω）（ω=2πf/fs为归一化频率，f为频率）从阵列的θ角方向入射时，波束形成器的空间响应为

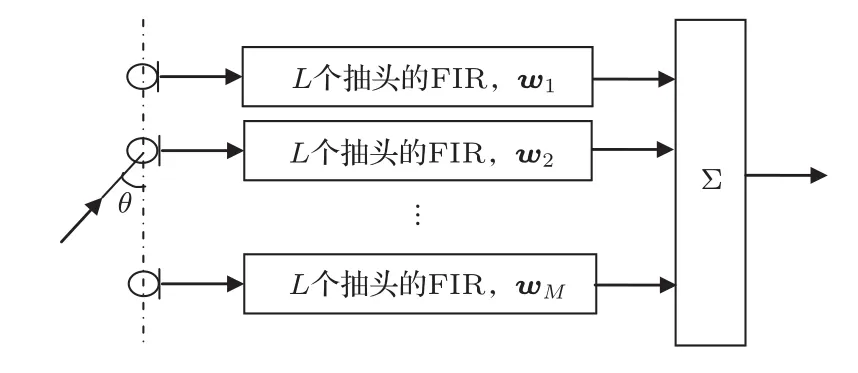
图1　时域宽带波束形成器结构图Fig.1 Time-domain broadband beamformer configuration

式（1）中，w为宽带波束形成器的权值，g（ω，θ）表示阵列的导向矢量，（·）T表示矩阵转置。宽带波束形成器的权值为其中，am表示第m个传声器的增益特性，γm表示第m个传声器的相位特性。传声器特性参数给定时，导向矢量（ω，θ）可以写成：

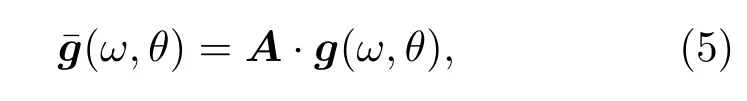
A是由传声器特性参数组成的ML×ML维的对角矩阵：

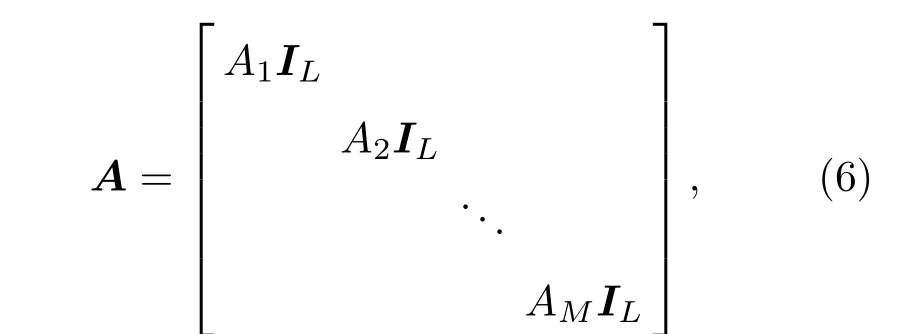
其中，IL是L维的单位矩阵。由式（1）和式（5），给定传声器特性参数时的波束响应为

2.2基于失配误差概率密度函数的稳健宽带波束

形成器设计

在宽带波束形成器的设计中，根据不同的代价函数可以设计不同性能的波束形成器。由于加权最小二乘法具有无需迭代、计算复杂度低等优点［13］，文献［7］根据平均性能最优的准则设计了加权最小二乘法稳健宽带波束形成器，即概率密度法。当传声器阵元存在增益和相位误差时，其代价函数为

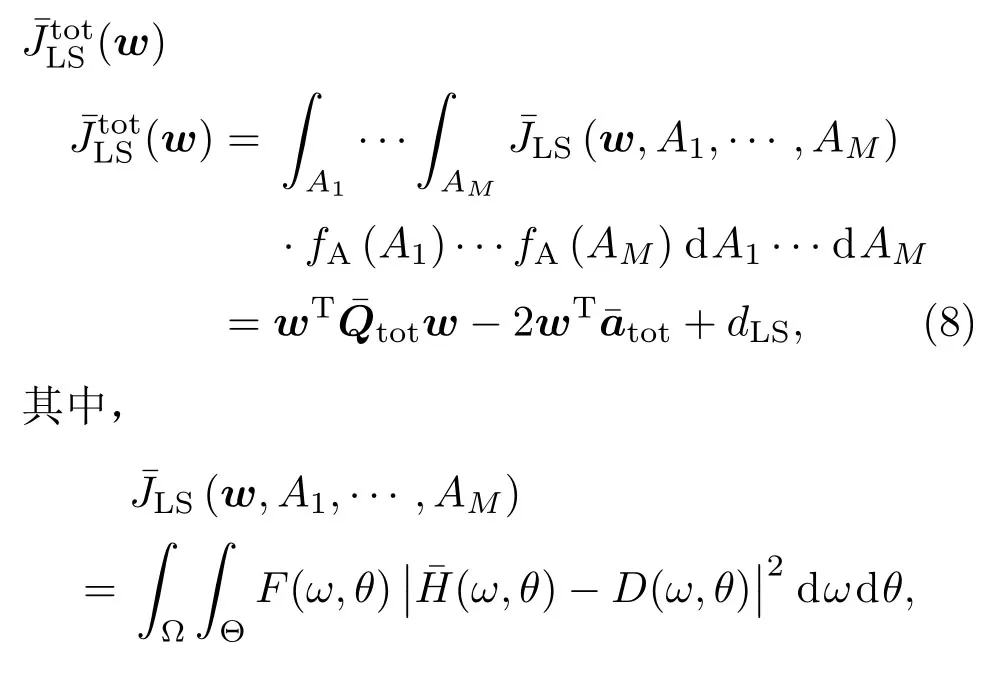
F（ω，θ）为加权函数，用来控制各空间频点对应误差权重的大小，D（ω，θ）为期望波束响应。fA（A）是随机变量A=ae-jγ的概率密度函数，即随机变量a（增益）和γ（相位）的联合概率密度函数，fA（A）= fα，r（a，γ）。如文献［7］，假设fA（A）与频率和角度无关，且所有的传声器特性Am，m=1，2，…，M具有相同的概率密度函数fA（A），并假设a和γ是相互独立的随机变量，则fA（A）=fα（a）fr（γ），其中fα（a）是增益的概率密度函数，fr（γ）是相位的概率密度函数。

3　基于失配误差低阶统计量的稳健宽带波束形成器设计

3.1固定加权最小二乘法

正如前文所述，采用概率密度法设计的稳健宽带波束形成器可以减小阵元增益和相位误差对波束形成器性能的影响，但概率密度函数信息在实际中较难获取，而一阶和二阶统计量信息较易获取。基于此，本节将探讨根据阵元失配误差的低阶统计量设计稳健宽带波束形成器的问题。

对于失配误差较小的情况，根据式（4），传声器特性参数的一阶泰勒近似可表示：

特别地，根据式（10）、式（11）和式（28）、式（29）可以得出，当传声器阵元只存在增益误差时，概率密度法和低阶统计量法设计出的稳健宽带波束形成器具有相同的权系数，即两者等价。综上所述，基于传声器失配误差低阶统计量的稳健宽带波束形成器的设计步骤如表1所示。

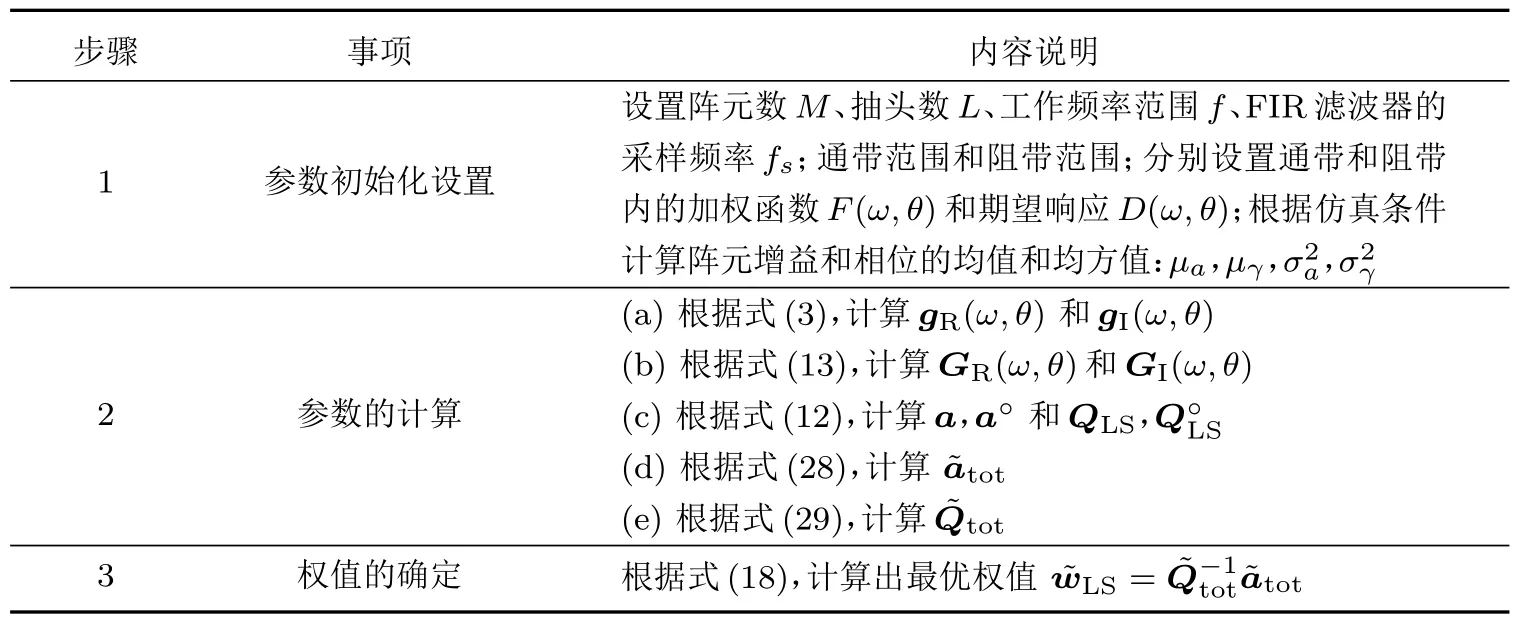
表1　低阶统计量法稳健宽带波束形成器的设计步骤Table 1 Design procedure of robust broadband beamformers using lowerorder statistics

根据式（28）和式（29）可知，通过该方法设计稳健宽带波束形成器时，需要利用传声器阵元增益和相位的一阶、二阶统计量，而根据式（10）和式（11）可知，概率密度法除了需要知道传声器阵元增益的一阶、二阶统计量外，还需要知道相位的概率密度函数信息。相比较而言，一阶和二阶统计量比概率密度函数更容易获取，因此，本文研究的低阶统计量法比概率密度法的实用性要强。

3.2变加权最小二乘法

在固定加权的最小二乘波束形成器设计中，加权函数F（ω，θ）是固定的常数，未在不同的空间频点处对误差权重进行控制，波束形成设计的自由度没有得到充分利用。研究表明，通过优化加权函数F（ω，θ）可以充分利用波束形成设计的自由度，从而进一步提高波束形成器的性能［8］。由于加权函数F（ω，θ）是非线性、非凸的，给加权函数的优化设计带来了困难。而从自适应阵列理论的观点来看待这个问题时，可以把加权函数F（ω，θ）看作从角度θ方向入射到阵列上的频率为ω的干扰信号的强度。一个自适应阵列对一个干扰信号的响应取决于该干扰信号的强度：干扰信号越强，所得波束图的增益越低［14］。因此，通过控制加权函数F（ω，θ），即变加权最小二乘法，可以实现对宽带波束形成器的通带赋形。

文献［8］的研究结果表明，概率密度法稳健宽带波束形成器的代价函数可以表示成Tikhonov正则化的形式。类似地，低阶统计量法的代价函数也可以表示成Tikhonov正则化的形式，即对应的代价函数式（17）与式（30）等价：

本节将采用迭代的方法设计变加权稳健宽带波束形成器，并保持阻带处于较低的增益水平，同时假设期望方向的波束响应为实数。在通带范围内，加权函数Fp（ω，θ）为［14］

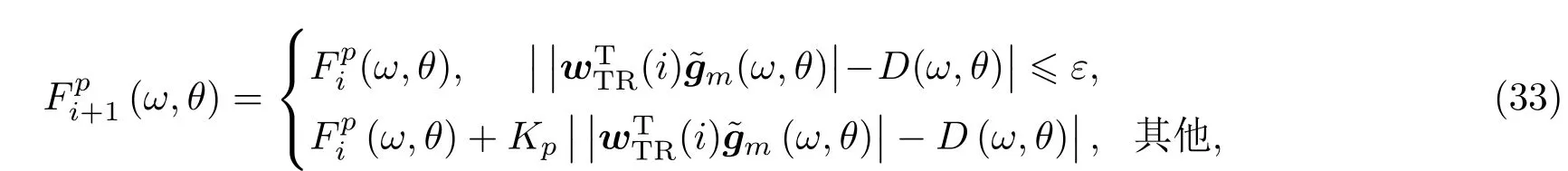
其中，i表示第i次迭代，ε是事先设定的通带内设计波束响应与期望波束响应间的允许误差；Kp是通带内的迭代增益。wTR（i）是第i次迭代时得到的权值。

在阻带范围内，加权函数Fs（ω，θ）为

综上，基于低阶统计量的变加权最小二乘稳健宽带波束形成器的设计步骤如表2所示。

表2　低阶统计量法通带赋形稳健宽带波束形成器的设计步骤Table 2 Design procedure of robust broadband beamformers with passband shaping using lower-order statistics

3.3与概率密度法的关系讨论

根据文献［8］和第3.2节的分析，我们知道，概率密度法和低阶统计量法的代价函数均可写成Tikhonov正则化的形式。下面，我们通过比较这两种方法的代价函数对所设计的波束形成器的性能进行分析。

概率密度法的代价函数式（8）表示成Tikhonov正则化的形式为［8］

由上述分析可知，虽然低阶统计量法只利用了阵元失配误差的低阶统计量信息，但所设计的代价函数与概率密度法代价函数相当，从而两种方法所设计波束形成器的波束图和稳健性相当。该结论进一步说明，在小误差条件下，阵元失配误差的高阶统计量信息在设计稳健波束形成器时是冗余的。因此，与概率密度法相比，低阶统计量法在保证所设计波束形成器的性能相当的条件下，实用性更强。

4　仿真实验与分析

4.1仿真实验I

本节对基于低阶统计量的固定加权最小二乘波束形成器进行仿真，并与概率密度法进行性能比较。设感兴趣的信号频率范围为f=［500，4000］Hz，采样频率fs=8000 Hz，通带范围为［70°，110°］，阻带范围为［0°，50°］∪［130°，180°］，声速c=340 m/s。假设传声器个数M=10，每个传声器的间隔为d=0.04 m。FIR滤波器抽头的个数与波束形成器的性能和实现复杂度有关：通常情况下，抽头个数越多，波束形成器性能越好，但实现复杂度也会增加，反之亦然［15］。为降低波束形成器的复杂度，同时保证波束形成器正常工作，本文设计抽头数L=20。以失配误差均匀分布的传声器为例，比较概率密度法和低阶统计量法所设计波束形成器的性能。仿真结果均由100次蒙特卡洛实验获得。当阵元的增益误差范围为=［-0.15，0.15］，相位误差范围为=［-5°，5°］，非稳健最小二乘法设计的宽带波束形成器的波束图如图2所示，第2.2节概率密度法设计的稳健宽带波束形成器的波束图如图3所示，第3.1节低阶统计量法设计的稳健宽带波束形成器波束图如图4所示。

对比图2～4可看出，当传声器阵元存在失配误差时，非稳健最小二乘法设计的宽带波束形成器已失效；而稳健宽带波束形成器则可以正常工作，有效降低了波束形成器对阵元失配误差的敏感性。

当改变每个阵元所接的FIR滤波器抽头数和阵元失配误差分布范围时，采用概率密度法和低阶统计量法设计的稳健宽带波束图的性能如表3所示。由图3～4和表3的仿真结果可以看出，在传声器存在失配误差时，两种方法均具有良好的稳健性能，并且设计出的波束图性能相当，与3.3节得出的结论一致。

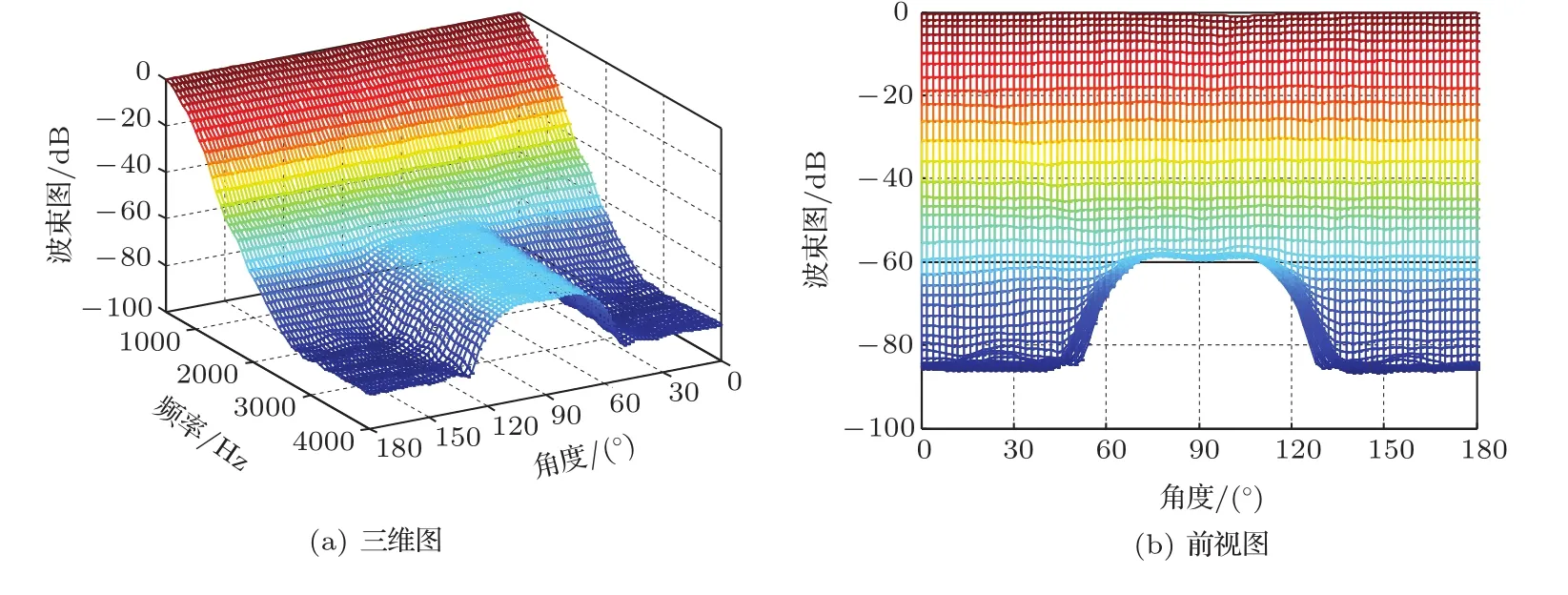
图2　非稳健最小二乘法设计的波束图Fig.2 Beampatterns of the non-robust least squares design

图3　概率密度法设计的波束图Fig.3 Beampatterns of the probability density design

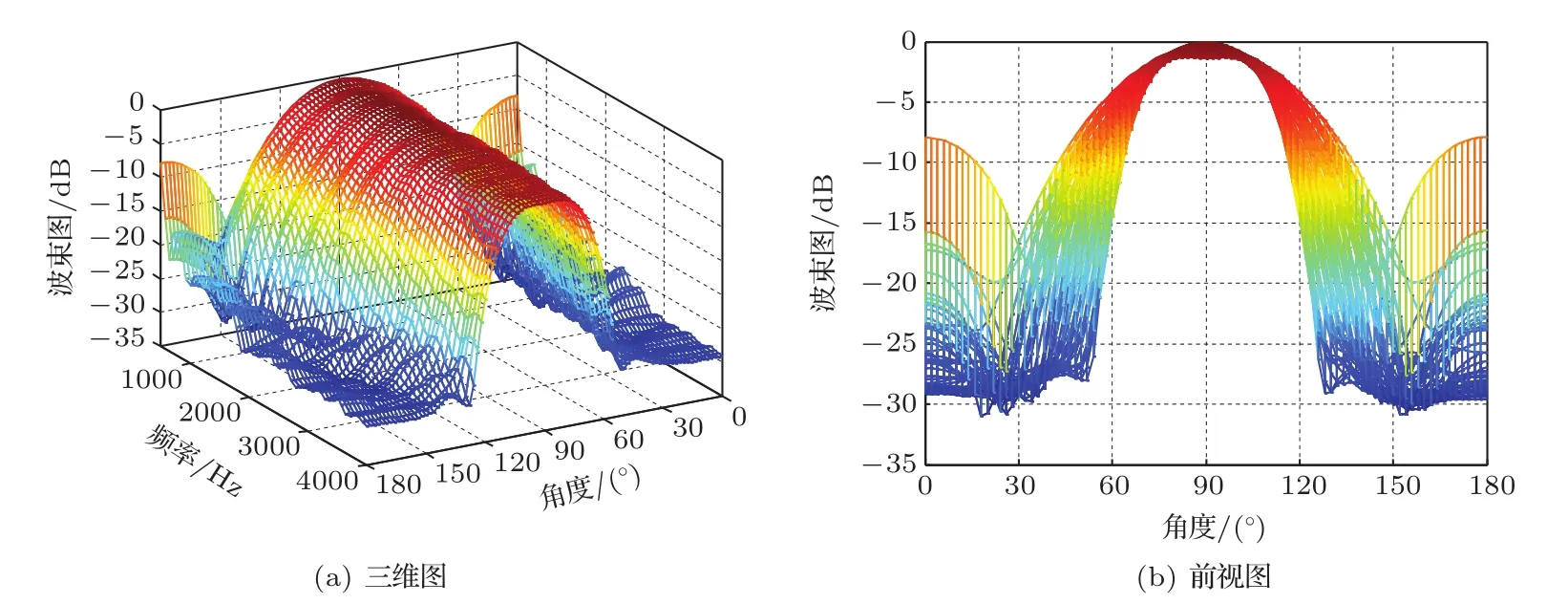
图4　低阶统计量法设计的波束图Fig.4 Beampatterns of the lower-order statistics design

由于低阶统计量法和概率密度法都是稳健的设计方法，而白噪声增益可以表征波束形成器的稳健性能：白噪声增益越大，稳健性能越好。因此我们通过比较这两种方法的白噪声增益来判断两种方法的稳健性能。宽带波束形成的白噪声增益定义为［16］

其中，g（ω，θs）表示期望方向θs的导向矢量。根据概率密度法和低阶统计量法计算出的权值w，可以分别计算这两种方法的白噪声增益。仿真结果表明，在通带范围的任意角度上，两种方法的白噪声增益具有相似的变化规律。因此本仿真实验以θs=90°为例，画出失配误差在3种不同范围内的白噪声增益曲线如图5所示。根据图5可知，两种方法的白噪声增益曲线基本重合，因此两种方法的稳健性能相当，与3.3节得出的结论也是一致的。

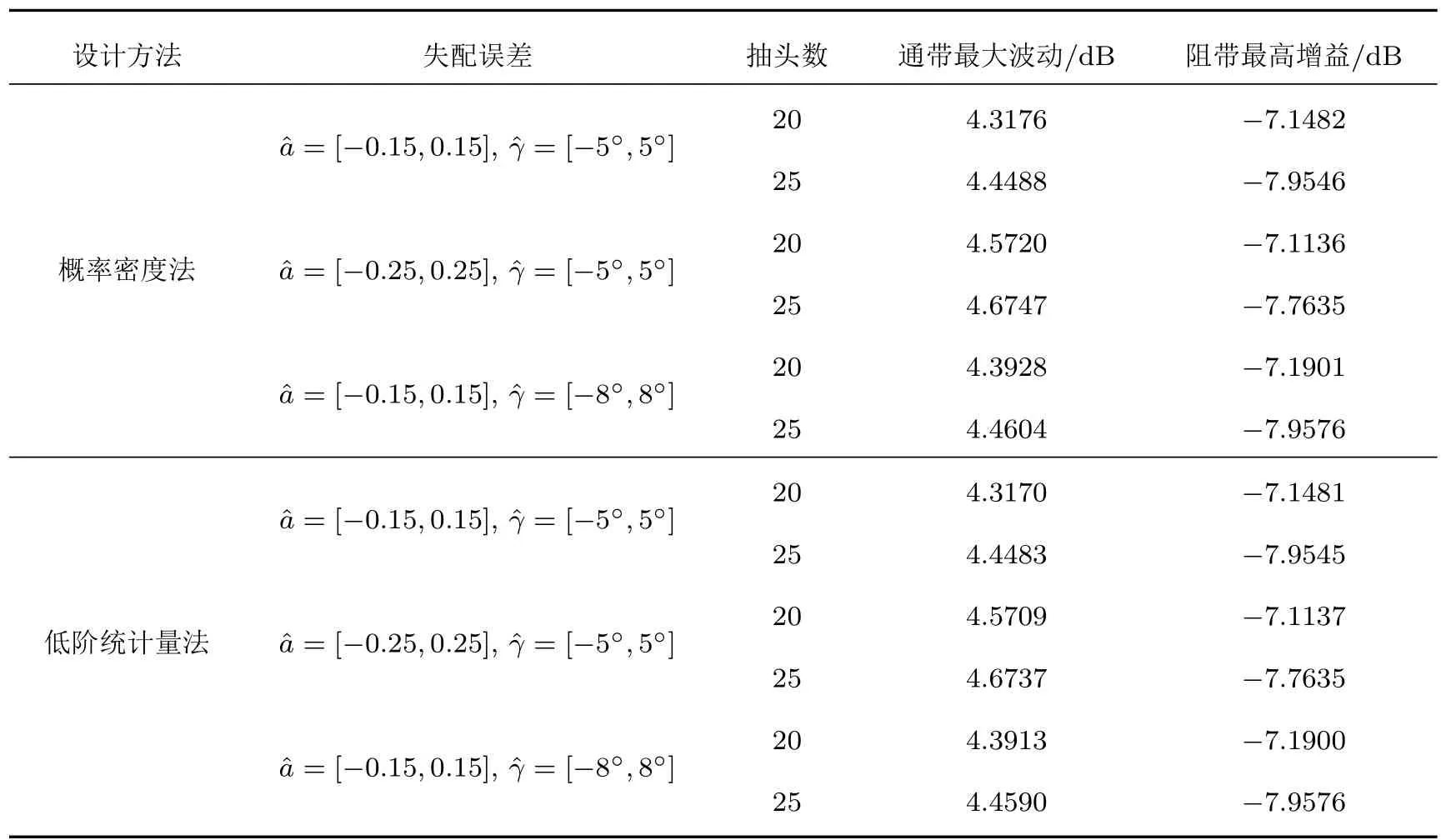
表3　两种稳健设计方法在不同条件下的结果Table 3 Results of two robust design methods under different conditions

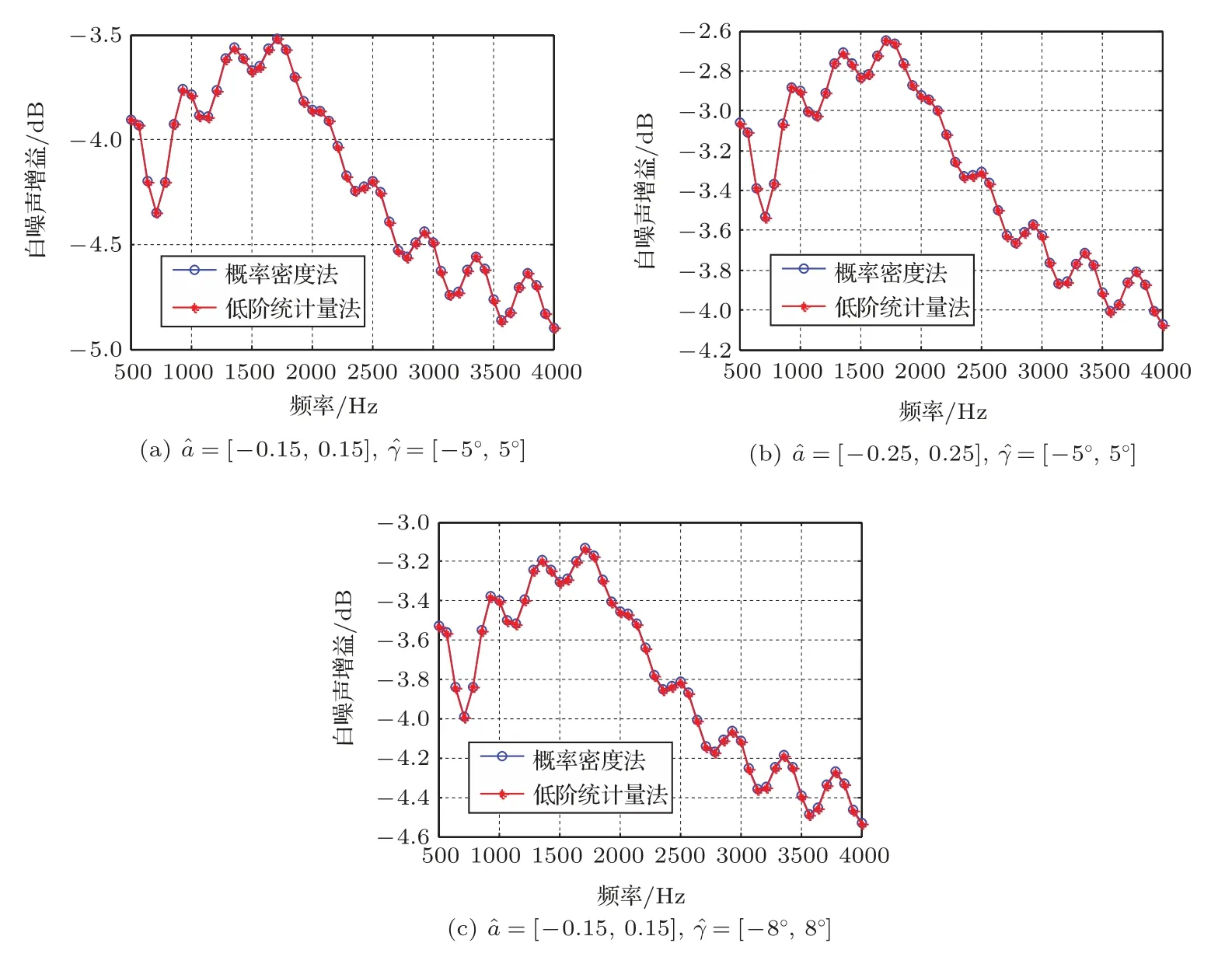
图5　概率密度法与低阶统计量法的白噪声增益曲线（θs=90°）Fig.5 White noise gain curves of the probability density and the lower-order statistics design（θs=90°）

4.2 仿真实验II

本节对低阶统计量法设计的具有通带赋形能力的变加权最小二乘波束形成器进行仿真，并与具有通带赋形能力的概率密度法进行性能比较。类似仿真实验I的仿真条件，设感兴趣信号的频率范围为f=［500，4000］Hz，采样频率fs=8000 Hz，声速c=340 m/s，传声器个数M=10，每个传声器的间隔为d=0.04 m，FIR滤波器抽头数L=20。考虑波束形成器的通带范围为［70°，110°］，阻带范围为［0°，50°］∪［130°，180°］，设置通带增益为1，即平顶通带宽带波束形成器。假设阵元的增益误差范围为=［-0.15，0.15］，相位误差范围为=［-5°，5°］，以失配误差均匀分布的传声器为例，比较两种通带赋形波束形成器的性能。仿真结果均由100次蒙特卡洛实验获得。图6所示为非稳健最小二乘法通带赋形后的波束图，图7所示为概率密度法通带赋形后的波束图。当对低阶统计量法设计的稳健宽带波束形成器进行通带赋形时，设置最大迭代次数T0=100，Kp=2000，Ks=1，ε=1×10-5，所得波束图如图8所示。

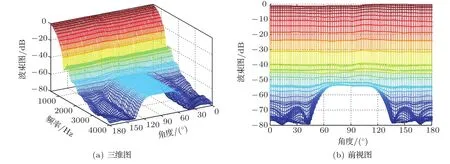
图6　非稳健通带赋形最小二乘法的波束图Fig.6 Beampatterns of the non-robust least squares design with passband shaping

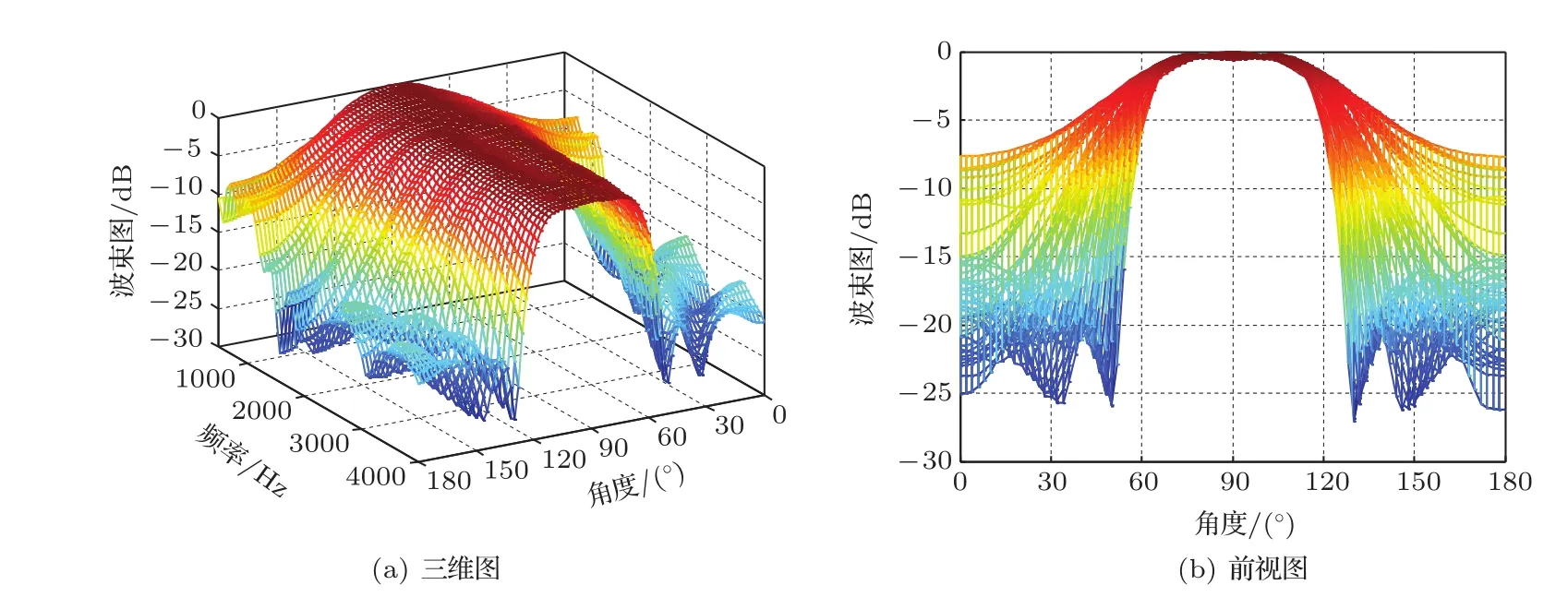
图7　通带赋形概率密度法的波束图Fig.7 Beampatterns of the probability density design with passband shaping

对比图6～8可以看出，当传声器阵元存在失配误差时，通带赋形后的非稳健最小二乘法仍然无法进行波束形成，而稳健的设计方法减小了阵元失配误差对波束形成器性能的影响。对比图4和图8可以看出，通带赋形优化技术不仅可以用于概率密度法，还可以用于低阶统计量法的设计中。对稳健宽带波束形成器进行通带赋形后，所得的波束响应更接近设置的期望响应D（ω，θ），通带范围内的最大波动得到降低：图4的通带最大波动为4.32 dB，而图8的通带最大波动仅为1.29 dB。

当分别改变每个阵元所接的FIR滤波器抽头数和阵元失配误差分布范围时，经过通带赋形技术所得概率密度法和低阶统计量法设计的稳健宽带波束形成器的波束图性能如表4所示。由表4可以看出，通带赋形低阶统计量法设计的波束图性能与通带赋形概率密度法相当。同固定加权最小二乘波束形成器类似，我们将通带赋形低阶统计量法和通带赋形概率密度法的白噪声增益进行对比，取θs=90°，失配误差在3种不同范围内所得白噪声增益曲线如图9所示。根据图9可以看出，通带赋形低阶统计量法的白噪声增益曲线与通带赋形概率密度法基本重合。因此，通带赋形低阶统计量法的稳健性能与通带赋形概率密度法相当。

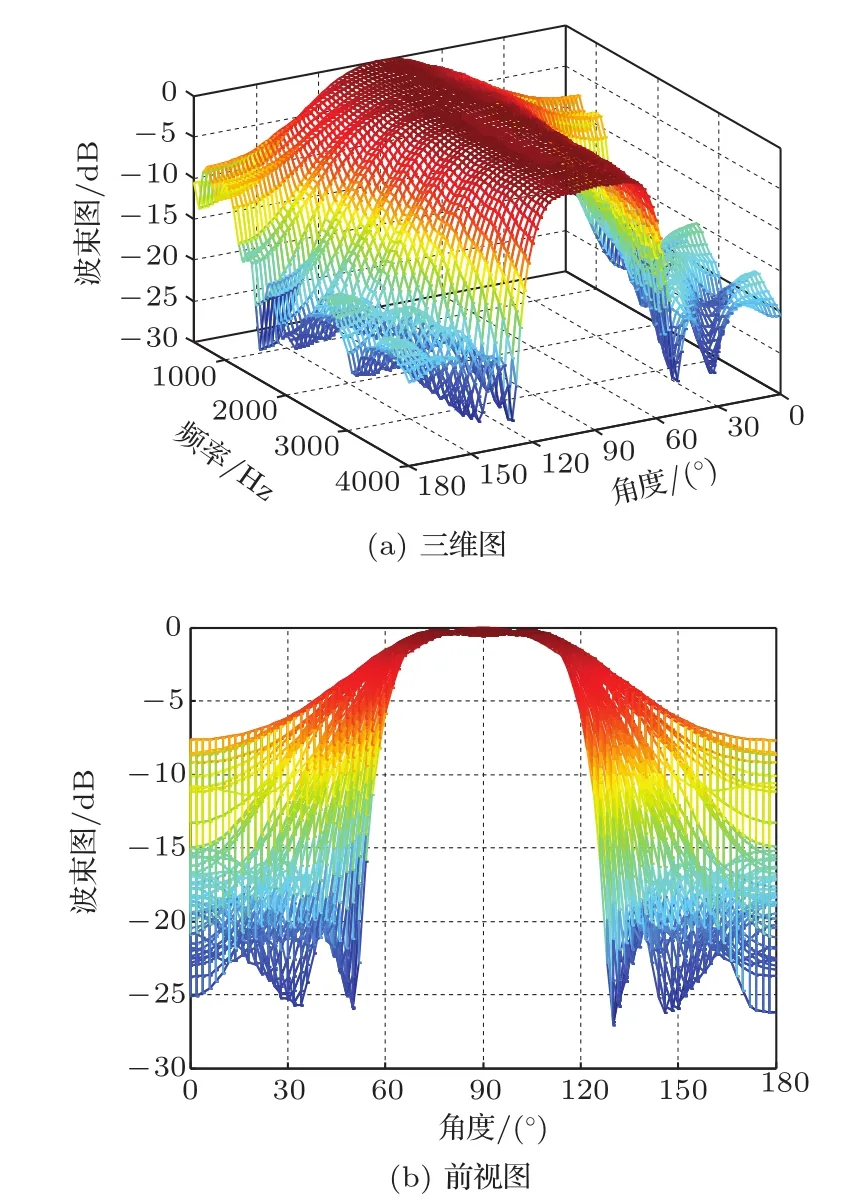
图8　通带赋形低阶统计量法的波束图Fig.8 Beampatterns of the lower-order statistics design with passband shaping

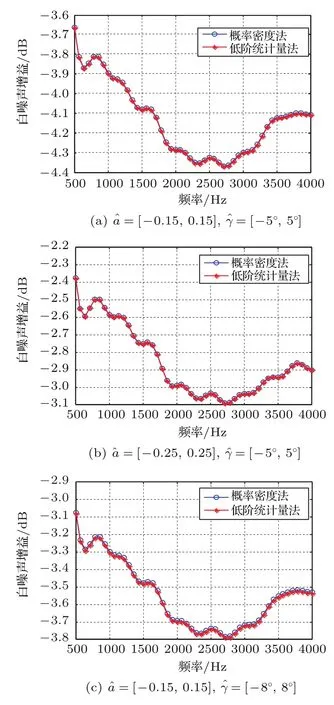
图9　通带赋形后，概率密度法与低阶统计量法的白噪声增益曲线（θs=90°）Fig.9 White noise gain curves of the probability density and the lower-order statistics design with passband shaping（θs=90°）

表4　两种通带赋形稳健设计方法在不同条件下的结果Table 4 Results of two robust design methods with passband shaping under different conditions

5　结论

本文研究了在传声器阵元存在失配误差情况下稳健宽带波束形成器的设计问题。针对概率密度法的失配误差概率密度函数信息在实际中较难获取的问题，本文提出了仅利用传声器阵元失配误差的低阶统计量信息设计稳健宽带波束形成器的方法，分别给出了固定权最小二乘和具有通带赋形能力的变加权最小二乘宽带波束形成器的设计理论。理论和仿真分析表明，在小误差条件下，概率密度法和低阶统计量法设计的波束形成器的波束图和稳健性能相当，从而进一步说明，阵元失配误差的高阶统计量信息在稳健波束形成器的设计中是冗余的。在实际中，由于一阶和二阶统计量较概率密度信息更易获取，因此低阶统计量法的实用性要优于概率密度法。

［1］陶建武.阵列信号处理在雷达和移动通信中的应用研究［D］.长春：吉林大学，2004.

［2］刘凯.声呐波束形成鲁棒性及算法研究［D］.哈尔滨：哈尔滨工程大学，2011.

［3］杨光，王福钋，李淑秋，等.并列式多入多出声纳宽带高分辨波束形成方法［J］.应用声学，2011，30（2）：131-137.

YANG Guang，WANG Fupo，LI Shuqiu，et al.A broadband high-resolution beam forming method for collocated multiple-input multiple-output sonars［J］.J.Appl. Acoust.，2011，30（2）：131-137.

［4］鄢社锋，马远良.传感器阵列波束优化设计及应用［M］.北京：科学出版社，2009.

［5］李静，陈华伟.基于正则化约束最小二乘的稳健频率不变波束形成器设计方法［J］.数据采集与处理，2012，27（2）：202-209.

LI Jing，CHEN Huawei.Robust FIB design using regularized constrained least squares［J］.Journal of Data Acquisition and Processing，2012，27（2）：202-209.

［6］甘甜，王英民.一种稳健的恒定束宽波束形成方法［J］.声学学报，2012，37（1）：18-24.

GAN Tian，WANG Yingmin.A robust broadband beam forming method of constant beam width［J］.Acta Acustica，2012，37（1）：18-24.

［7］DOCLO S，MOONEN M.Design of broadband beamformers robust against gain and phase errors in the microphone array characteristics［J］.IEEE Trans.Signal Process.，2003，51（10）：2511-2526.

［8］CHEN H W，SER W.Design of robust broadband beamformers with passband shaping characteristics using Tikhonov regularization［J］.IEEE Trans.Audio Speech Lang.Process.，2009，17（4）：665-681.

［9］CROCCO M，TRUCCO A.Stochastic and analytic optimization of sparse aperiodic arrays and broadband beamformers with robust superdirective patterns［J］.IEEE Trans.Audio Speech Lang.Process.，2012，20（9）：2433-2447.

［10］TRUCCO A，CROCCO M.Design of an optimum superdirective beamformer through generalized directivity maximization［J］.IEEE Trans.Signal Process.，2014，62（23）：6118-6129.

［11］DOCLO S，MOONEN M.Superdirective beamforming robust against microphone mismatch［J］.IEEE Trans.Audio Speech Lang.Process.，2007，15（2）：617-631.

［12］LAI C C，NORDHOLM S，LEUNG Y H.Design of robust steerable broadband beamformers incorporating microphone gain and phase error characteristics［C］.IEEE International Conference on Acoustics，Speech and Signal Processing，2011：101-104.

［13］卓光宇.宽带恒定束宽波束形成算法及其实现［D］.西安：西安电子科技大学，2010.

［14］ZHOU P Y，INGRAM M A.Pattern synthesis for arbitrary arrays using an adaptive array method［J］.IEEE Trans.Antennas and Propagation，1999，47（5）：862-869.

［15］陈华伟，王天南，张峰，等.基于抽头稀疏化的最小二乘频率不变波束形成器设计［J］.数据采集与处理，2014，29（2）：191-197.

CHEN Huawei，WANG Tiannan，ZHANG Feng，et al.A least square approach to the design of frequency invariant beamformers with sparse tap coefficients［J］.Journal of Data Acquisition and Processing，2014，29（2）：191-197.

［16］MICHAEL B，DARREN W.Microphone arrays：signal processing techniques and applications［M］.Germany：Springer-Verlag，2001.

Design of robust broadband beamformers based on lower-order statistics method

REN WeiyiCHEN HuaweiBAO Yu
（Nanjing University of Aeronautics and Astronautics，College of Electronic and Information Engineering，Nanjing 210016，China）

Since microphone arrays are highly sensitive to microphone mismatch errors，robust beamformer design has been studied extensively in the microphone array processing field.At present，the probability density function（PDF）based method is one of the important methods in robust beamformer design for microphone arrays.However，the PDF of microphone mismatch errors cannot be easily obtained in practice.To overcome this drawback，this paper studies a robust design method based on lower-order statistics of microphone mismatch errors.The proposed method uses only the first-and second-order statistics which are easier to obtain in practice.The design methodologies for fixed-weighted and varying-weighted least squares beamformers based on lower-order statistics of microphone mismatch errors are presented，respectively.Theoretical and simulation analysis show that the performance of the proposed beamformers is comparable to that of the beamformers designed via the PDF method under the condition of small microphone mismatch errors.

Broadband beamforming，Microphone array，Robustness

TN912

A

1000-310X（2015）05-0413-12

10.11684/j.issn.1000-310X.2015.05.006

2015-04-02收稿；2015-07-04定稿

*国家自然科学基金资助项目（61001150，61471190），教育部留学回国人员科研启动基金资助项目，中央高校基本科研业务费资助项目（NS2014041）

任维怡（1991-），女，江苏南通人，硕士研究生，研究方向：阵列信号与信息处理。

E-mail：hwchen@nuaa.edu.cn