MSK信号解调算法研究及其性能仿真比较

芮国胜，陈　强，田文飚，孙文军

（海军航空工程学院a.电子信息工程系；b.研究生管理大队，山东烟台264001）

MSK信号解调算法研究及其性能仿真比较

芮国胜a，陈强b，田文飚a，孙文军a

（海军航空工程学院a.电子信息工程系；b.研究生管理大队，山东烟台264001）

最小频移键控（MSK）信号具有相位连续、包络恒定并且带宽占用小的优点，被广泛应用于现代无线通信领域。对MSK解调算法进行了分析总结，将MSK解调算法分为逐符号检测算法和多符号检测算法。根据这两大类检测算法的核心思想，对算法的误码率性能、运算复杂度及应用环境进行了详细分析，总结归纳了各检测算法的优点及存在的问题。实际工程中考虑到接收机的可靠性和成本因素，可以在误码率性能和复杂度之间选取一个折衷，采用合适的解调算法。

最小频移键控；逐符号检测；多符号检测；相干解调；非相干解调

最小频移键控（Minimum Shift Keying，MSK）是一类信号包络恒定、相位连续、带宽占用小的调制技术，因其优良的频谱特性和功率特性，在现代无线通信领域中得到广泛的应用［1-2］。

随着MSK的发展，对MSK信号解调研究成为关注的焦点。包络非相干解调法、延迟差分解调法和正交相干解调法是经典的MSK逐符号检测算法［3-5］。对全响应MSK信号而言，逐符号检测算法具有较好的误码率性能，但是随着信号的部分响应长度增加，逐符号检测性能会变得越来越差［6］。多符号检测（Multiple Symbol Detection）最初是为了提高CPFSK信号的解调性能而提出的［7］。由于其利用前后码元的相关性来检测，有效解决了逐符号检测算法对部分响应长度的依赖，进而改善了有记忆调制系统的检测性能。

本文主要研究MSK各种解调算法基本原理及其误码性能比较。首先，在AWGN信道下，文中对MSK信号各种解调方法的检测原理进行研究，着重讨论了MSK的多符号检测算法；然后，从误码率性能及运算复杂度2个方面对各检测算法进行分析比较，并归纳总结各算法的优缺点；最后，分析了各算法的应用环境，并给出了相关解调方法应用的选取原则。

1　MSK信号及特点分析

MSK信号属于连续相位调制方式，是调制指数为0.5的CPFSK信号，其一般形式可表示为［8］：

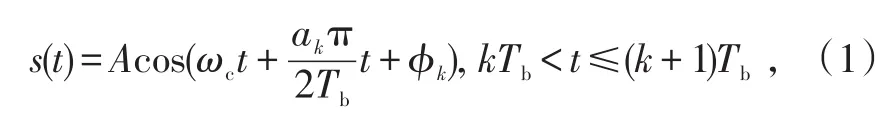
或者

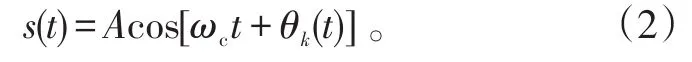
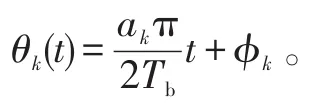
由式（1）可看出，当ak=+1时，码元频率 f1等于；当ak=-1时，码元频率 f2等于所以，f1和 f2频差Δf等于，这是保证2FSK信号正交的最小频率间隔［9］。

相位常数ϕk的选取应保证波形相位在码元转换时刻是连续的，因而可以导出相位递归条件：

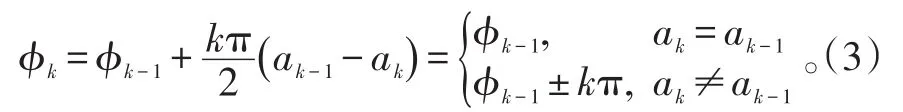
式（3）表明，第k个码元的相位ϕk不仅和当前的输入ak有关，而且和前一码元的相位及ak-1有关，也就是说MSK信号的前后码元之间存在相关性［10］。

2　MSK解调算法

MSK是一种特殊形式的CPFSK信号，结合MSK前后码元记忆的特性，根据观测码元长度，可将MSK解调算法分为逐符号检测法、多符号检测法2大类［6］。

2.1逐符号检测

逐符号检测法是指依据一个符号时间内的接收信号判决出当前符号信息，可分为相干检测法和非相干检测法［4］。在进行码元判决时相干检测需要估计载波相位，误码率性能较好；非相干检测无需相位同步，因而具有较好的抗相差性能，但误码率性能一般［11］。

本文主要对MSK信号的包络非相干解调法、延迟差分解调法以及正交相干解调法进行研究。

1）包络非相干解调。包络非相干解调法的原理是将接收到的MSK信号下先变频得到基带信号；然后，将基带信号分别与2路正交基函数组成的相关滤波器在一个符号时间内作相关运算，并对相关器的输出结果进行平方率检波，选择判决量最大的作为输出。解调原理如图1所示。由于包络非相干解调算法是依据接收信号的包络信息进行符号判决，因而该解调算法具有较好的抗相差性能［2］。

图1　包络解调原理框图Fig.1 Principle diagram of envelop demodulation

2）延迟差分解调。常用一比特延迟法和二比特延迟法［5］。一比特延迟差分解调法是指将通过中频滤波器滤除带外噪声后的接收信号分为2路，其中一路信号延迟Tb时间，并相移π/2，另一路信号保持不变，然后将2路所得信号相乘，结果经过低通滤波器和抽样判决单元即可得到码元判决信息，见图2。

图2　一比特延迟差分解调原理框图Fig.2 Principle diagram of one-bit differential detection

3）正交相干解调。MSK正交相干解调采用图3所示的接收框图。将接收到的MSK信号分I、Q 2个支路，分别与同相、正交分量相乘并积分，上下支路的积分区间都是2Tb。然后，在t=（2k+1）Tb、t=（2k+2）Tb时刻抽样判决，判决后的数据经过并串变换输出。

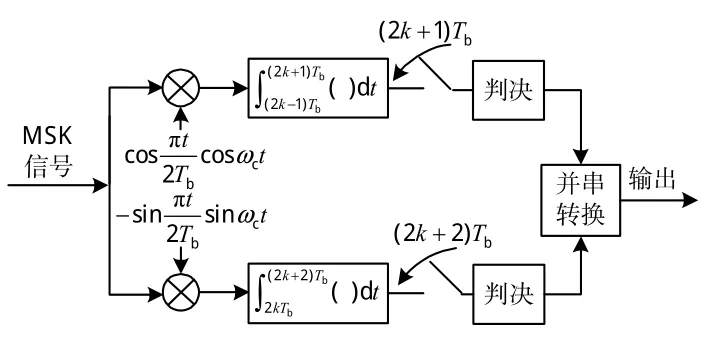
图3　正交相干解调原理框图Fig.3 Principle diagram of orthogonal coherent detection

2.2多符号检测法

对于无记忆调制信号，在最小码元错误概率意义上，逐符号检测法是最佳的。对于有记忆调制信号而言，算法的检测性能一般较差［12］。与逐符号检测不同，经典多符号检测算法是指通过观测接收信号的多个符号，完成当前符号的判决输出。由于多符号检测充分考虑了接收信号的记忆特性，与逐符号检测相比可获得更优的检测性能，保证了系统传输的可靠性。同逐符号检测算法一样，经典多符号检测也可以分为相干多符号检测和非相干多符号检测。

1）相干多符号检测［7］。相干多符号检测算法是通过观测接收信号的N个符号，完成第1个符号的检测。不妨设一次观测的接收信号为：

式中，s（t，a1，Ak）是与数据符号序列相对应的MSK信号，a1为要检测的第1个符号，为a1之后N-1个比特的所有可能的数据序列。

对于相干检测，信号初始相位已知，不失一般性，可假定为0。

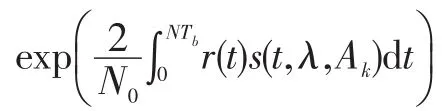
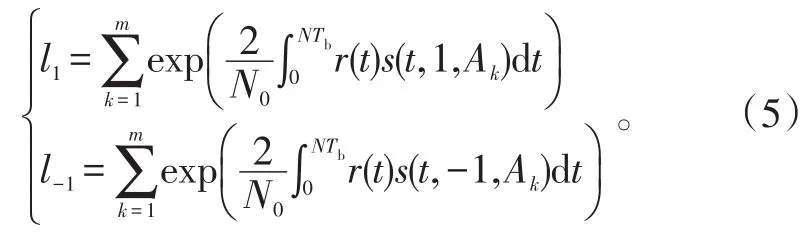
接收机选择较大者对应的数据符号a1作为判决输出。相关器的输出定义为 xλk（λ=1或 -1，k=1，2，…，m），

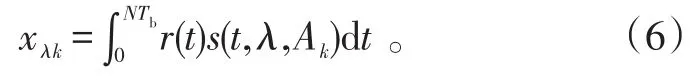
那么，似然函数可以记为

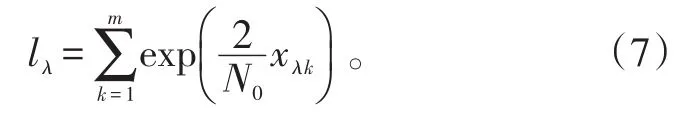
由式（7）可以看出，似然函数lλ的计算量随着观测长度N的增大而指数增加，因而当N很大时，要分析最佳接收机确切的误码率性能不太可能。但在高信噪比下，可以将最佳接收机简化成次佳接收机。

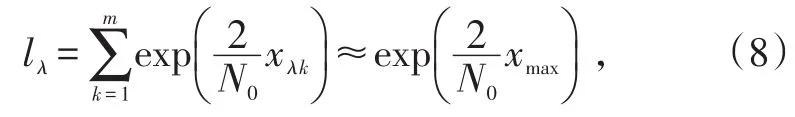
更进一步，由于exp（）是单调递增函数，因而xmax可以作为用于判决的等价参数。因此，图4中的次佳接收机无须求指数函数和求和模块直接检测相关器的输出，判断最大的xmax相应的a1为判决值，这简化了算法的计算量。

MSK的最佳接收机和高信噪比下的次佳接收机如图4所示。

图4　MSK的最佳接收机和次佳接收机Fig.4 MSK best and suboptimal coherent receiver

2）非相干多符号检测。对于非相干检测，载波初始相位ϕ是未知的。假定ϕ服从0到2π的均匀分布，其概率密度函数为：

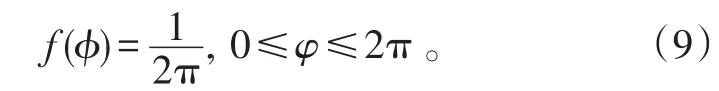
与相干多符号检测不同，非相干多符号检测是指通过观测接收信号r（t）的（2n+1）个符号，完成中间比特的判决和输出［7］。采用简化符号将信号表示为：

Δk总共有 μ=22n个序列，所有的序列是等概率的，即Δ的概率密度为 f（Δ）=1/μ。

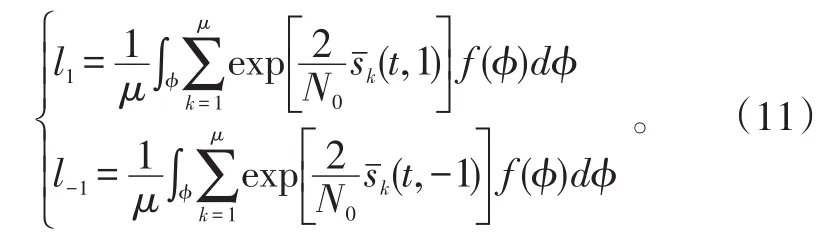
式（11）中：

对相位进行平均的结果为零阶修正贝塞尔函数，因此有：

式（13）中：

MSK的最佳非相干接收机和高信噪比下的次佳非相干接收机如图5所示。图5中，所有的积分区间为0到（2n+1）Tb。与相干检测类似，可以得到高信噪比下的次佳接收机。

图5　MSK的最佳非相干接收机和次佳非相干接收机Fig.5 MSK best and suboptimal noncoherent receiver

在高信噪比下有如下近似式：

式（16）中，zimax为zik的最大值，而且贝塞尔函数为单调递增函数。因此，次佳接收机只须要考察所有zik，然后选择最大zik对应的an+1作为判决值。

3　仿真实验

对上述解调算法进行误码率性能仿真及运算量比较，并进行分析和总结。

3.1性能仿真

性能仿真主要包括2个部分：第1部分是分别在理想同步、定时误差和载波相差3种情况下对各种检测算法进行误码率仿真；第2部分是不同的观测长度N对多符号检测算法的误码率性能仿真。仿真基于Matlab平台，参数设置为：AWGN信道；载波频率fc=1；码元宽度Tb=1；采样速率 fS=10；序列长度L=5×105；其中，第1部分中观测长度N设置为5。

1）理想同步。图6给出了理想同步条件下各MSK检测算法误码率性能比较，其中多符号检测算法的观测长度N=5。可以看出，正交相干解调法与相干多符号检测法的检测性能相当，明显优于其他解调算法，按照解调性能区分依次为非相干多符号检测、差分解调、包络检波。另外，由仿真结果可以看出，在误码率为10-3时，正交相干解调算法的解调性能优于非相干多符号检测法0.5dB，相比差分解调法则提高了2dB。非相干多符号检测算法、包络检波以及差分解调法同属于非相干解调方式，但是，在相同的误码率性能条件下，非相干多符号检测算法明显优于差分解调法和包络检波法的误码率性能。

图6　理想同步下系统误码率性能比较Fig.6 System error performance comparison under ideal synchronization

2）定时误差。为了比较定时误差对于MSK解调算法的影响，设计新的仿真实验。图7是在定时误差为Tb/10情况下进行性能仿真的。由1）的仿真结果可知，包络检波法、差分解调法和非相干多符号检测法性能并无明显下降，非相干解调算法具有较好的抗时差性能；而正交相干解调算法和相干多符号检测算法的检测性能急剧下降，在误码率为10-2时，其误码率性能损失了约5dB，这也说明了相干解调算法严重依赖于定时误差的准确性。

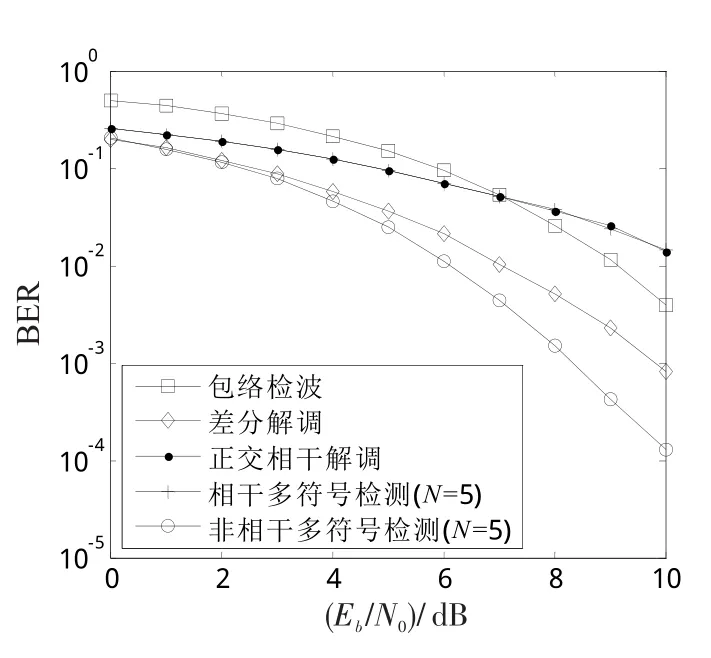
图7　定时误差下误码率性能比较Fig.7 System error performance comparison under timing error

3）载波相差。进一步地研究载波相差对算法性能的影响。图8给出了载波相差为π/10情况下的仿真结果。由图8可知，正交相干解调法和相干多符号检测法的检测性能相当，相比于图6，误码率性能下降明显，这说明相干解调算法的抗相差性能较差；而包络检波、差分解调法以及非相干多符号检测算法的误码率性能基本不受相差影响。

图8　载波相差下误码率性能比较Fig.8 System error rate performance comparison under carrier phase difference

4）观测长度。图9给出了多符号检测算法中不同观测长度条件下的误码率。由图9可知，随着观测长度N的增加，多符号检测算法的误码率性能变好。其中，非相干多符号检测算法的误码率性能随观测长度N的增加逐渐改善，当N→∞时趋近于相干最优的检测性能曲线；然后，对于相干多符号检测算法，当N=3时可以达到相干最优的检测性能。总体来讲，相干解调算法的性能优于非相干类解调算法。当误码率为10-3时，相比于非相干多符号检测算法（观测长度分别为N=3、N=5、N=7），相干解调算法的性能分别提高了约2.3dB、0.6dB、0.3dB。

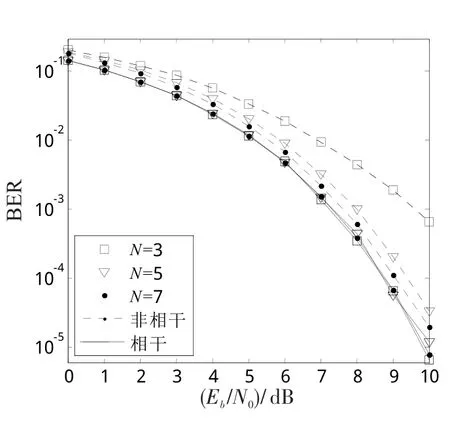
图9　不同观测长度N下多符号检测算法的误码性能比较Fig.9 System error performance comparison of multi-symbol detection algorithm with different observation lengthN

3.2应用环境分析

经过上述仿真比较，可以得出以下结论：

1）从检测的误码率性能而言，同等条件下，相干解调的误码率性能要优于非相干解调的，多符号检测算法的误码率性能要优于逐符号检测算法。

2）从抗时差和相差性能而言，非相干检测算法由于在解调时无需进行载波相位同步，相比于相干检测算法，具有较强的抗时差能力和抗相差能力。

3）从工程实现的难易程度而言，与非相干解调算法相比，相干解调算法需要对接收信号进行载波相位同步，在快衰落信道下，难以取得理想的同步效果。与逐符号检测算法相比，随着观测长度N的增加，多符号检测算法的接收机所需相关器的个数将成指数增长，当N很大时，接收机结构十分复杂，现实中难以实现。

4　结论

文中对MSK信号的解调算法进行了研究，分析并对比了各种解调算法的误码性能。仿真结果表明：在不同的解调环境下，每种解调算法各具优缺点。实际中，可以根据接收机误码率性能需求以及客观的检测环境，在误码率性能和复杂度之间选取一个折衷，采用合适的解调算法。

［1］吴伟仁，刘旺旺，蒋宇平，等.国外月球以远深空探测的发展及启示［J］.深空探测研究，2011，9（3）：1-10. WU WEIREN，LIU WANGWANG，JIANG YUPING，et al.The revelation from the development of foreign deepspace exploration beyond the moon［J］.Deep Space Exploration，2011，9（3）：1-10.（in Chinese）

［2］KOM I.GMSK with limiter discriminator detection in satellite mobile channel［J］.IEEE Transactions on Communications，1991，39（1）：94-101.

［3］DEBUDA R.Coherent demodulation of frequency-shift keying with low deviation ratio［J］.IEEE Transactions on Communications，1972，20（3）：429-435.

［4］吴伟仁，节德刚，丁兴文.深空测控通信中GMSK体制非相干解调算法研究［J］.宇航学报，2014，35（12）：1437-1443. WU WEIREN，JIE DEGANG，DING XINGWEN.A noncoherent demodulation algorithm of GMSK for deepspace missions［J］.Journal of Astronautics，2014，35（12）：1437-1443.（in Chinese）

［5］SIMON M K，WANG C C.Differential detection of Gaussian MSK in mobile radio environment［J］.IEEE Transactions on Vehicular Technology，1984，33（4）：307-320.

［6］李宝龙.深空通信中CPM信号的非相干多符号检测研究［D］.南京：南京航天航空大学，2012：8-12. LI BAOLONG.Noncoherent multi-symbol detection of CPM signals in deep-space communications［D］.Nanjing：Nanjing University of Aeronautics and Astronautics，2012：8-12.（in Chinese）

［7］OSBORNE W P，LUNTZ M B.Coherent and noncoherent detection of CPFSK［J］.IEEE Transactions on Communications，1974，22（8）：1023-1036.

［8］GRONERNEVER S A，MCBRIDE A L.MSK and offset QPSK modulation［J］.IEEE Transactions on Communications，1976，24（8）：809-820.

［9］XIE DINGXIN，HE JING，CHEN LIN，et al.Data-aided channel estimation and frequency domain equalization of minimum-shift keying in optical transmission systems［J］. Chinese Optics Letters，2014，12（4）：1-5.

［10］樊昌信，曹丽娜.通信原理［M］.7版.北京：国防工业出版社，2015：231-242. FAN CHANGXIN，CAO LINA.Principles of Communications［M］.7thed.Beijing：National Defense Industry Press，2015：231-242.（in Chinese）

［11］漆钢，肖仕伟，张伟.极小BT突发GMSK信号定时恢复算法及性能分析［J］.太赫兹科学与电子信息学报，2013，11（4）：547-551. QI GANG，XIAO SHIWEI，ZHANG WEI.Performanceanalysis and simulation of timing recovery for burst GMSK signals with small BT［J］.Journal of Terahertz Science and Electronic Information Technology，2013，11（4）：547-551.（in Chinese）

［12］丁兴文，朱智勇，李海涛.基于维特比算法的GMSK信号非相干解调技术研究［J］.遥测遥控，2011，32（1）：18-21. DING XINGWEN，ZHU ZHIYONG，LI HAITAO.Noncoherent demodulation with viterbi decoding for gmsk signals［J］.Journal of Telemetry Tracking and Command，2011，32（1）：18-21.（in Chinese）

Demodulation Algorithm Reasearch and Performance Simulation of MSK Signals

RUI Guoshenga，CHEN Qiangb，TIAN Wenbiaoa，SUN Wenjuna
（Naval Aeronautical and Astronautical University a.Department of Electronic and Information Engineering；b.Graduate Students’Brigade，Yantai Shandong 264001，China）

MSK has the advantages of constant envelope and continuous phase，is widely used in wireless communication. The demodulations technologies including multiple symbol detection and symbol-by-symbol detection were analyzed in this paper.Furthermore，the performance simulation and algorithm’s complication were compared with each other，and the advantages and the problems of these methods were summarized.Finally，considering the factor of actual applications and the cost，the appropriate methods could be adopted to reach a trade-off between performance and complicity.

minimun shift keying；symbol-by-symbol detection；multiple-symbol detection；coherent demodulation；non⁃coherent demodulation

TN911

A

1673-1522（2015）06-0505-06DOI：10.7682/j.issn.1673-1522.2015.06.002

2015-07-04；

2015-09-06

国家自然科学基金资助项目（41476089）；“泰山学者”建设工程专项经费基金资助项目

芮国胜（1968-），男，教授，博士，博导。