基于改进圆域分割方法的混沌微弱信号检测

谢永兴，黄　隽，胡云安，林　涛

（海军航空工程学院a.研究生管理大队；b.指挥系；c.控制工程系；d.科研部，山东烟台264001）

基于改进圆域分割方法的混沌微弱信号检测

谢永兴a，黄隽b，胡云安c，林涛d

（海军航空工程学院a.研究生管理大队；b.指挥系；c.控制工程系；d.科研部，山东烟台264001）

针对Melnikov方法和Lyapunov指数法在确定Duffing振子混沌阈值时计算繁琐、耗时较长的问题，提出基于改进圆域分割的相图识别方法。以圆域内相点比例为指标，利用其在系统相变时急剧变化这一特性进行微弱信号的检测。改进圆域分割方法的圆域半径取值更加灵活，使混沌阈值的确定更加方便。仿真实验表明，信噪比为-60dB时检测正确率达89%，验证了该方法的有效性。

Duffing振子；改进圆域分割；信号检测；微弱信号

微弱信号检测是研究如何从强噪声中提取有用信号，或者如何提高检测系统输出信号的信噪比［1］。运用微弱信号检测技术可以测量到传统观念认为不能测量的微弱量，使测量精度得到较大的提高。微弱信号检测技术在许多领域具有广泛的应用，例如物理学、化学、生物医学、天文学、地学、雷达、声纳、振动测量、故障诊断、通信等。其应用的广泛性和迫切性促使人们不断探索与研究微弱信号检测的新理论、新方法，以期能更快速、更准确地从强噪声背景中检测出微弱信号。

微弱信号检测方法主要分为基于线性理论的时域、频域、时频域方法和基于非线性理论方法［2-4］。国外研究者将混沌理论应用于微弱信号检测始于20世纪90年代，为混沌理论的工程应用开辟了新领域，探索了实现微弱信号检测的新途径。

1992年，Brown等人［5］首先提出了应用Duffing振子的初值敏感性构造传感器的3种方法；Birx等人采用复映射前向反馈神经网络（Complex Mapping Feed Forward Networks，CMFFNS）识别Duffing方程相平面的变化，从而检测出随机高斯噪声背景下的信号，检测信噪比可达-12dB［6］。

我国在利用混沌振子检测微弱信号领域的研究也不断取得新的进展。1997年，王冠宇等在Birx工作的基础上利用Duffing振子对白噪声背景下微弱正弦信号的检测进行研究［7］，实现了频率已知情况下幅度的测量。在此基础上，他描述了Duffing振子混沌系统的分岔规律［8］，并基于间歇混沌原理提出了利用混沌振子阵列的方法检测微弱信号的频率，并将可检测信噪比范围扩展到-68dB。聂春燕［9］将现代谱估计方法与Duffing振子系统构成混合检测系统，并使用Melnikov方法求解出现混沌的阈值。张宾［10］将Lyapunov特性指数作为混沌判据引入微弱信号混沌检测领域，为混沌检测提供了一种量的标准。李月等人［11］先从非线性方程理论出发论证混沌系统存在周期解，再用定向过零技术计算谐波频率。

微弱信号检测过程中混沌阈值的确定极其重要，而无论是Melnikov方法，还是Lyapunov指数法，这些解析方法，其具体实现计算繁杂、耗时过长，无法满足实际工程应用中的快速性要求。文献［12］提出了用于快速识别相变的圆域分割（CZP）方法，在一定程度上提高了相变的识别效率。本文针对同频正弦信号的检测展开研究，对CZP方法进行改进，采用圆域内相点比例P作为系统状态的判别指标，首先通过考察P随Duffing振子驱动力幅值的变化，利用相变前后P的取值也会产生跳变这一特性确定P的阈值，然后就可以将待检信号输入临界混沌状态的Duffing振子中，计算输出相图的P值，利用获得的阈值作为判据，判断信号存在与否。

1　Duffing振子检测原理

考虑如下Duffing振子［11］：

式（1）中：k为阻尼比；-x（t）+x3（t）为非线性恢复力；γ为内置驱动力幅值；input由待检同频周期信号s（t）和零均值高斯白噪声n（t）组成，即input=s（t）+n（t）；ε为常系数，用于控制加入到Duffing振子中input信号的功率强度。

取t=ωτ，式（1）变为

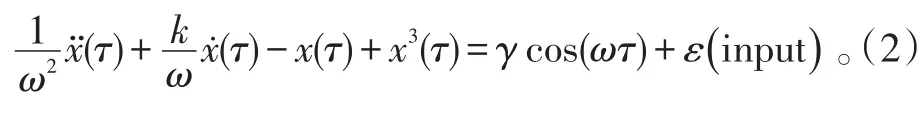
式（2）中，ω=2πf，f为待检信号频率。

因为式（2）是由式（1）推导而来，x（τ）为x（t）在另一时间尺度上的表示，所以其动态特性和临界值保持不变。

为得到Duffing振子的计算模型，取 y1=x，，将式（2）重写为状态方程形式：

进一步写成矩阵的形式有：

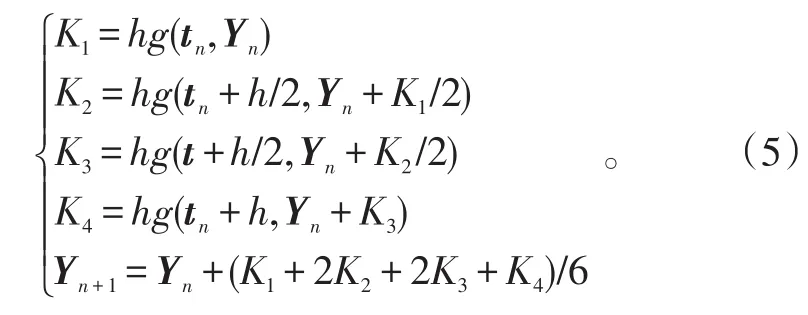
式（5）中：tn=n×h（n=1，2，…）和Yn（n=1，2，…）为第n步计算时的时间和状态向量。

2　圆域分割方法及其改进

圆域分割（CZP）方法，即在振子规则环状轨道内部设置一个圆形区域，通过轨迹是否穿越圆域边界来识别s（t）的存在。CZP方法的具体判定规则是：如果轨迹接触或穿越边界，则s（t）不存在；反之，如果轨迹没有触及或穿越边界，则s（t）存在。详细实现步骤如下。

1）求得由信号s（t）及内置驱动力共同作用下的Duffing振子相轨迹图，在其轨迹内设置一尽可能大的圆域，圆域半径记作R。

2）用高电平表示相轨迹没有进入圆域（s（t）存在），低电平代表相轨迹触及或进入圆域（s（t）不存在）。

3）取高电平为1、低电平为0，圆域边界作为阈值，圆域分割器可表示为：

CZP方法存在的问题有：仅仅用相轨是否穿越圆域边界来判定信号存在并不合理，因为由于噪声的影响，周期轨道会比无噪声时显得更加粗糙，造成部分点落入圆域内部，从而引起误判；另外，圆域半径R要求“尽可能大”，没有定量的指标对R的选取进行指导。针对CZP方法的不足进行改进，提出改进圆域分割方法，即圆域半径取值大到圆域边界和相轨相交，通过考察圆域内部相点所占比例来判定待检信号有无。具体实现如图1所示，其中no、ni分别表示同一时间段圆域外和圆域内相点计数值，记圆域内相点比例为

图1　改进圆域分割法实现Fig.1 Implementation of ICZP method

由图2可知，系统处在混沌态时的圆域内相点比例相对较大；而系统一旦进入大周期状态，圆域内相点比例将明显地减小。这种阶跃性的跳变对划定门限进行信号有无的判决十分有利。因此，本文利用圆域内相点比例来判决系统状态的改变。此时问题转化为判决问题：

式中，Pc为判定阈值。

图2　Duffing振子的2种相图Fig.2 Two states of Duffing oscillator

3　仿真分析

在式（3）中取ε=1，系统方程变为：

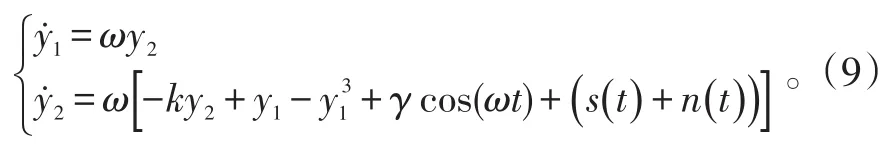
不失一般性，假设加入的待检测同频信号为s（t）=acos（ωt），其中，角频率 ω=10 rad/s，幅度a=0.000l，n（t）为零均值高斯白噪声，此时驱动力总幅值变为A=γ+a。利用Melnikov方法和仿真分析可得，当k=0.5时，Duffing系统式的阈值γc≈0.826 5。当A＞γc时，系统将进入大周期态；反之，则处于混沌态。因此，先将Duffing振子检测系统调整到临界状态（γ=0.826 5），然后将含噪待检信号（s（t）+n（t））加到Duffing系统的驱动力项；利用四阶Runge-Kutta法求解 Duffing系统，取时间步长 h=0.01，初值为（y1，y2）=（0.8，0.9）。根据Duffing系统的解，利用式计算圆域内相点比例与事先设定的判决阈值Pc比较，从而判定信号的有无。根据多次实验所得圆域内相点比例变化图，当圆域半径R=1.5时，取Pc=0.4。

图3 a）～c）为圆域半径R=1.5加入不同强度噪声时圆域内相点比例P随驱动力总幅值A的变化情况。图3 d）～f）为圆域半径R=1.4加入不同强度噪声时圆域内相点比例P随驱动力总幅值A的变化情况。

图3　圆域内相点比例变化图Fig.3 Variations graphs of phase point percentage within the circle area

由图3 a）～c）可知，不同噪声强度下圆域内相点比例整体变化趋势是一致的，在驱动力幅值A=0.826附近急剧下降，对应于Duffing系统由混沌临界状态转变为大尺度周期态。另外，随着噪声强度的加大，过渡阶段的波动增多，这将直接影响混沌阈值的选取以及后期信号检测的正确率。由图3 d）～f）可知，不同噪声强度下圆域内相点比例整体变化趋势是一致的，在驱动力总幅值A=0.826附近急剧下降，对应于Duffing系统由混沌临界状态转变为大尺度周期态。随着噪声强度的加大，过渡阶段的波动也逐渐增多。需要注意的是，同等噪声强度下，其圆域内相点比例P整体比R=1.5时低。所以，可以取不同圆域半径进行微弱信号的检测，并相应地调整阈值即可。

为检验所提算法的有效性，实验时待检测信号s（t）=0.000 1cos（10t）保持不变，加入不同强度的噪声。每种噪声水平重复进行实验1 000次，最终的统计结果见图4。由图可知，当信噪比SNR=-50dB时，改进圆域分割方法的检测概率还能保持在100%，比文献［13］整整降低了20dB；当信噪比为-60dB时，检测正确率高达89%；当信噪比小于-72dB时，检测性能急剧下降，到-80dB时正确检测概率已不足25%。

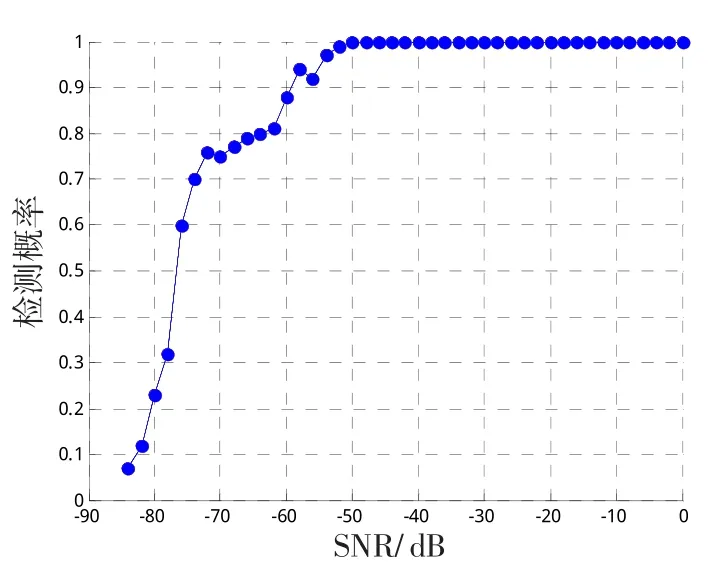
图4　检测性能曲线Fig.4 Detection performance curve

仿真分析时需注意以下几点：

1）仿真中仅对角频率为10rad/s的单频信号进行了检测分析，而根据Melnikov方法计算混沌跃迁阈值的过程可知，Duffing系统的混沌阈值并不随频率的变化而变化。

2）对于与系统驱动力频率存在频差和相差的待检信号，可以通过构造振子阵列进行未知频率信号的检测；因为频差和相差会导致间歇混沌，进一步导致判决门限的变化，须仔细考虑如何调整判决门限，确保判决的正确性。

3）仿真实验中，圆域半径取值采用的是略小于各相点到原点的平均欧氏距离，保证了圆域内总有一部分相点存在，此时圆域内相点比例约为32%左右。

4　结论

本文提出了一种改进圆域分割方法，以圆域内相点比例作为指标进行微弱信号的定量检测。圆域内相点比例能够比较实时地表征系统的动力学行为，有利于提高相图识别的快速性。圆域半径取值不唯一，提高了该方法的灵活性。仿真分析表明，当信噪比为-60dB时，检测正确率达89%，验证了该方法的有效性。尽管文中检测采用的是单频信号，但该方法可以推广至方波信号、直扩信号、BPSK信号的检测，只是需要调整相应判决门限。如何自适应地调整检测门限、提高算法的实用性将是下一步需要研究的问题。

［1］戴逸松.微弱信号检测方法及仪器［M］.北京：国防工业出版社，1994：1-2. DAI YISONG.Weak signal detection method and instrument［M］.Beijing：National Defense Industry Press，1994：1-2.（in Chinese）

［2］夏均忠，刘远宏，冷永刚，等.微弱信号检测方法的现状分析［J］.噪声与振动控制，2011，31（3）：156-161. XIA JUNZHONG，LIU YUANHONG，LENG YONGGANG，et al.Analysis of methods of weak signal detection［J］.Journal of Noise&Vibration Control，2011，31（3）：156-161.（in Chinese）

［3］夏均忠，刘远宏，马宗坡，等.基于调制随机共振的微弱信号检测研究［J］.振动与冲击，2012，31（3）：136-140. XIA JUNZHONG，LIU YUANHONG，MA ZONGPO，et al.Weak signal detection based on the modulated stochastic resonance［J］.Journal of Vibration and Shock，2012，31（3）：136-140.（in Chinese）

［4］王永生，刘爱东，高绍嵩，等.Duffing振子临界态性能研究［J］.海军航空工程学院学报，2008，23（6）：669-673. WANG YONGSHENG，LIU AIDONG，GAO SHAOSONG，et al.Research on the performance of the duffing oscillator critical states［J］.Journal of Naval Aeronautical and Astronautical University，2008，23（6）：669-673.（in Chinese）

［5］BROWN R，CHUA L O，POPP B.Is sensitive dependence on initial conditions nature’s sensory device［J］.International Journal of Bifurcation Chaos，1996，2（1）：193-199.

［6］BIRX D L，PIPENBERG S J.Chaotic oscillators andcomplex mapping feed forward networks（CMFFNS）for signal detection in noisy environments［C］//International Joint Conference on Neural Networks.1992：881-888.

［7］王冠宇，陶国良，陈行，等.混沌振子在强噪声背景信号检测中的应用［J］.仪器仪表学报，1997，18（2）：209-212. WANG GUANYU，TAO GUOLIANG，CHEN XING，et al.Application of chaotic oscillator in signal detection under strong noise background［J］.Chinese Journal of Scientific Instrument，1997，18（2）：209-212.（in Chinese）

［8］WANG G，CHEN D，LIN J，CHEN X.The application of chaotic oscillators to weak signal detection［J］.IEEE Transactions on Industrial Electronics，1999，46（2）：440-444.

［9］聂春燕，石要武，衣文索.测量任意周期信号的混沌解判定［J］.电子测量与仪器学报，2005，19（4）：12-14. NIE CHUNYAN，SHI YAOWU，YI WENSUO.Determing chaotic solution to measure arbitrary periodic signals［J］.Journal of Electronic Measurement and Instrument，2005，19（4）：12-14.（in Chinese）

［10］张宾，李月，马海涛.微弱信号混沌检测临界阈值的Lyapunov指数算法［J］.地球物理学进展，2003，18（4）：748-751. ZHANG BIN，LI YUE，MA HAITAO.An algorithm based on Lyapunov exponents to determine the threshold of chaotic detection for weak signal［J］.Progress in Geophysics，2003，18（4）：748-751.（in Chinese）

［11］李月，杨宝俊，邓小英，等.谐波信号频率的混沌检测方法［J］.电子与信息学报，2005，27（5）：731-733. LI YUE，YANG BAOJUN，DENG XIAOYING，et al.The chaotic detecting method for the frequency of harmonic signal［J］.Journal of Electronics&Information Technology，2005，27（5）：731-733.（in Chinese）

［12］FU Y，WU D，ZHANG L，et al.A circular zone partition method for identifying Duffing oscillator state transition and its application to BPSK signal demodulation［J］.Science China（Information Sciences），2011，54（6）：1274-1282.

［13］魏恒东，甘露，李立萍.基于哈密顿量的Duffing振子微弱信号检测［J］.电子科技大学学报，2012，41（2）：203-207. WEI HENGDONG，GAN LU，LI LIPING.Weak signal detection by duffing oscillator based on hamiltonian［J］. Journal of University of Electronic Science and Technology of China，2012，41（2）：203-207.（in Chinese）

Chaotic Weak Signal Detection Based on Improved Circle Zone Partition Method

XIE Yongxinga，HUANG Junb，HU Yun’anc，LIN Taod
（Naval Aeronautical and Astronautical University a.Graduate Students’Brigade；b.Department of Command；c.Department of Control Engineering；d.Department of Scientific Research，Yantai Shandong 264001，China）

To solve the complex computation and time consuming problem when determining the threshold value of chaos state of Duffing oscillator using Melnikov method and Lyapunov exponent method，improved circle zone partition（ICZP）method was presented to identify the phase state.ICZP method uses phase point percentage within the circle area to deter⁃mine the phase state，which will change dramatically when the state changes from chaos to periodic state.This characteris⁃tic was used to perform weak signal detection.The radius of the circle zone may take different values，which makes it more convenient to determine the chaos threshold.The simulation showed that the detection accuracy could reach up to 89% even when the signal to noise ratio（SNR）got as low as-60dB，which proved the validity of the proposed method.

Duffing oscillator；improved circle zone partition；signal detection；weak signal

TN911.23

A

1673-1522（2015）06-0511-05DOI：10.7682/j.issn.1673-1522.2015.06.003

2015-06-28；

2015-09-21

航空科学基金资助项目（20140184001）

谢永兴（1985-），男，博士生。