四狼大围捕兔子巧脱险

在正方形的中心坐着一只兔子，在四个顶点上各有一只狼.如果狼只能沿着正方形的边跑，且狼的最大速度是兔子最大速度的1.4倍.试问兔子能否从正方形中逃出？（1985年莫斯科数学竞赛题）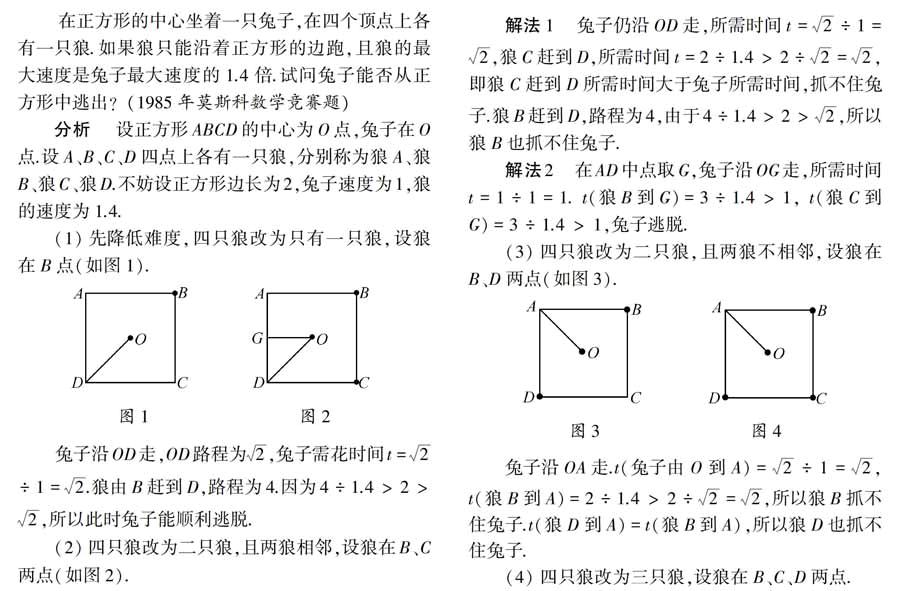

分析 设正方形ABCD的中心为O点，兔子在O点.设A、B、C、D四点上各有一只狼，分别称为狼A、狼B、狼C、狼D.不妨设正方形边长为2，兔子速度为1，狼的速度为1.4.

（4）四只狼改为三只狼，设狼在B、C、D两点.

解法1 如图4，兔子沿OA走，t（兔子由O到A）=2÷1=2，t（狼B到A）=2÷1.4>2÷2=2，即t（狼B到A）>2，狼B抓不住兔子.又因为t（狼D到A）=t（狼由B到A），t（狼C到A）>t（狼D到A），所以狼D、狼C也抓不住兔子.

解法2 如图5，在CD上取一点E，使DE=0.01.过E作EM∥AD交OD于M，过M作MF∥CD交AD于F，连接EF交OD于N，兔子视情况沿ONE或沿ONF走.

t（兔子沿ONE走）=t（兔子沿ONF走）=t（兔子沿OD走）=2÷1=2，t（狼C到F）>t（狼C到E）=1.99÷1.4>1.981÷1.4=1.415>2，狼C抓不住兔子.t（狼B到F）=t（狼B到E）>t（狼C到E），狼B更抓不住兔子.兔子现在可以不考虑狼B和狼C了，只要对付好狼D就行了.兔子先由O走到N点，观察一下狼D的位置（记狼D此时位置为P）.若P在DC上（不包括D），兔子沿NF走.t（兔子由N到F）=时间（兔子由D到F）÷2<时间（兔子由D到F）÷1.4=时间（狼D由D到F）

（5）当四只狼坚持岗位.

如图6（图中，E、M、F、N位置同图5），兔子沿ON走，走到N点时，观察狼D该时刻的位置P，若P在DC上（不包括D），兔子沿NF走，若P在AD上（不包括D），兔子可沿NE走，若P刚好就在D点上，兔子沿NE或沿NF走均可，但无论走那条路线，兔子所花t均为2.由（4）的解法2知兔子能逃脱狼B、狼C、狼D的追捕，而t（狼A到E）>t（狼A到F）=t（狼C到E）=1.99÷1.4>1.981÷1.4=1.415>2，狼A同样也抓不住兔子.因此兔子完全可以逃脱“四狼大围捕”！

反思 本题是一道较复杂和困难的竞赛题，题中兔子所走路径、四只狼所走路径看似都可以千变万化、你变我也变，呈现出一派纷繁复杂的图象，令人难以梳理，但其结果却是出人意料的简单.这里我们采用的解题策略是：先把问题退到一个最简单地方，着手解决这个最简单的问题，再逐步加深问题，而对每一步所加深的问题，都想全想透，让每一步启发着下一步，这样，一步一步进而解决原先较难的问题.事实上，这种“退”的方法，在当代数学的研究中应用非常广泛，同时这种方法也是学习数学、思考数学、研究数学的好方法.

作者简介 蔡历亮，男，中国数学会会员，发表文章50余篇.