用定义导航数学思考
蔡卫兵
以已有的知识为基础,设计一个陌生的数学情景,并给出一个新的定义,要求使用新给出的定义作出某种判断或计算、推理、迁移,我们不妨称这类试题为“新定义”试题.这类问题关键在于阅读,核心在于理解,目的在于应用.其重点考查考生的阅读理解能力、接受能力、应变能力和创新能力,培养学生自主学习、主动探究的品质.纵观北京市2012年至2015年的中考数学试卷,“非常距离”、“关联点”、“有界函数、边界值”、“反称点”闪亮登场;纵观宁波市2011年至2015年的中考数学试卷,“奇异三角形”、“n阶准菱形”、“和谐四边形”、“三分线”、“智慧角”更是犹如一棵“常青树”屡见不鲜,但这些考题区分度比较大,学生的得分率比较低.事实上,“给什么,用什么”是解答这类试题的基本思路,通过不断地回到定义去进行数学阅读、信息获取和加工以及反思概括,强化对概念之间联系的关注,从而让定义导航数学思考,使问题的解答在定义的启发下拾级而上.
1 拨云见雾取真经
有些新概念包含4个要素,即概念的名称、定义、例子和属性.有时为更简洁地反映异类对象在数与形方面内在、固有的属性,还会引进反映本质特征的符号和图形来表示定义的内涵.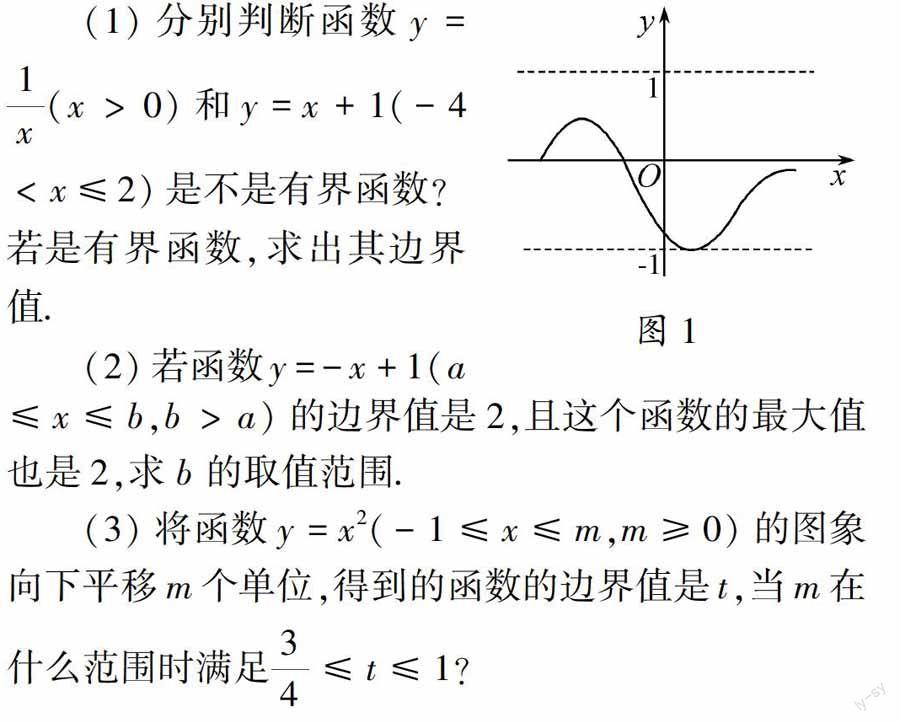

例1 (2014年北京卷第25题)对某一个函数给出如下定义,若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值,例如,图1中的函数是有界函数,其边界值是1.图1
(1)分别判断函数y=1x(x>0)和y=x+1(-4 (2)若函数y=-x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b 的取值范围. (3)将函数y=x2(-1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值是t,当m在什么范围时满足34≤t≤1? 此题中有两个新的概念,一个是有界函数,这个新概念中包含实数M>0的存在性和函数值y满足-M≤y≤M的任意性,抽象难理解,通过数形结合借助直观的图像便能获得图形语言,有界函数的图像必须夹在平行于x轴的两条平行线之间;另一个是边界值,在所有满足条件的M中M的最小值,这对新概念的理解是只停留在直接性理解层次,往往在解答问题时不会用这个概念,只有深刻理解概念的内涵和外延,能揭示概念之间的联系,把握边界值概念中的M是指什么,来源于何处?如何求M的最小值,这与函数有何关系?透过现象看本质,函数的边界值M0就是函数的最小值、最大值的绝对值中较大的一个,拨云见雾取真经,边界值问题可转化为函数的最值问题.因此在数形结合思想和转化与化归思想的引领下进行解答: 2 回归本源化矛盾 “新定义”压轴题为有效地检测出学生在新概念的学习活动中的一系列表现,往往设计成一个有条理的分层级问题串,各小题之间会按某种逻辑递进展开,在探究和应用环节时易受其他信息的干扰,学生在解题过程中会忽视一些关键属性和概念之间的联系. 例2 (2015年宁波卷第25题)如图2,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA·OB=OP2,我们就把∠APB叫做∠MON的智慧角. 此题清晰地展示了一类课题学习的研究模式:定义——问题——判断——探究——应用.问题涉及单动点和旋转问题、相似三角形的判定和性质、反比例函数的性质、曲线上点的坐标与方程的关系等知识,要求学生通过阅读理解、判断推理、操作计算、分类讨论等方式进行即时的学习和研究.问题的设置起点低、梯度明显,有利于不同层次学生的发挥,有利于考查学生数学素养和潜能.第(3)问重视学生对新知识的理解和应用能力,而学生关注的重点在反比例函数y=3x和条件BC=2CA,忽视∠AOB的智慧角∠APB的顶点P的特征而无从下手. 回归本源化矛盾,不但可以促进对新概念本质属性的把握,而且还会强化学生对概念之间联系的关注,∠AOB的智慧角∠APB的顶点P在∠AOB的平分线上,要求点P的坐标,只需求出OP的长度,而∠APB绕点P旋转时始终满足OA·OB=OP2,因此将问题转化为综合运用相似三角形、反比例函数等知识求OA·OB的值.因此在智慧角定义的导航下进行思考和解答: 3 “新定义”压轴题的教学思考 “回到定义去”是一种元认知监控,即对思维的起点和方向进行思维监控,并适时调控自己认知的过程,这是波利亚怎样解题表中的一条基本原则.对于立意鲜明、背景深刻、情境新颖、设问灵活的“新定义”压轴题,由我们曾经学过的定义派生出新定义,虽然在题目的外表上作了变化,而实际还是用已学过的知识和方法来解决问题,变的是我们对题目的认识,不变的是我们对新题型解决的方法和数学思想.但因具有信息量大,学生不易深入理解新定义与各小题之间的内在联系以及问题中其他信息的干扰,所以我们更应仔细阅读,拨云见雾取真经,不断地把文字语言、符号语言、图形语言相互转化,透过现象看本质,抽丝剥茧现原形,同时不断地“回到定义去”,回归本源化矛盾,真正把握新概念的本质属性,关注新概念之间的联系,在定义的导航下对问题的认识得到加深,解题思路得到拓展,解题效率得到提高. 李邦河院士曾说过“数学,根本上是玩概念的”.象本文一定意义上也是在倡导“玩概念”,对于引导重视概念教学无疑是十分有利的,关注学生参与和体验,注重学生自主学习能力、类比、拓展、迁移能力的培养,能够转变学生学习数学的方式,实现数学语言的相互转换,扩展学生的数学思维,提高学生掌握知识的水平.特别是在解题教学中,它可以是新的概念、新的运算、新的符号、新的图形、新的定理或新的操作规则与程序、新的情境等等,注重学法指导,引导“学生回到定义去”,如果能及时地“回到定义去”,则往往能有效地达到解决问题的目的,让定义导航着我们的数学思考,是一个重要的解题策略.然而,要使学生养成“回到定义去”的思考习惯,则需要平时在“做”的过程和“思考”的过程中不断积累. 参考文献 [1] 李梦虎,蒋荣清.学生解答新概念型问题的困惑及教学对策[J].中国数学教育(初中版),2014(12):51-55. [2] 贾俊.把关预设新定义 “距离”考题频登场[J].中学数学(初中版),2015(7):44-46.

中学数学杂志(初中版)2015年5期
