微积分在大学物理中的应用分析

王金华

（天津职业技术师范大学理学院，天津300222）

微积分在大学物理中的应用分析

王金华

（天津职业技术师范大学理学院，天津300222）

结合大学物理中的一些实例，具体分析了微分、导数、积分、微分方程、近似等在大学物理中的应用，旨在为学生应用微积分研究分析和解决物理问题提供思路，更好地促进大学物理的学习。

大学物理；微积分；微分方程；近似法；导数

数学是解决物理问题的重要基础。运用数学知识定义物理概念、推导物理定律，可使物理问题变得简洁，并能定量地解决问题。微积分发明以后，数学在物理学中的作用更为显著。牛顿利用微积分来解决运动学问题，论证了万有引力定律；麦克斯韦将微积分与电磁理论结合得到麦克斯韦方程组，推动了电磁理论的诞生。在大学物理教学中，微积分的应用是学生理解和解决物理问题的重点和难点。本文结合物理教学中的一些典型实例，如微分方程、中值定理、泰勒公式等来着重讨论大学物理课程中常用的微积分知识及相关应用，帮助学生在大学物理的学习中把微积分知识与物理问题有机结合起来，掌握解决物理问题的思路与方法，更好地促进大学物理课程的学习。

1　导数方法

导数是一个量在某一点附近的变化率，处理物理问题时经常需要利用导数来求物理量的变化率。如力学问题中已知运动方程，利用位移对时间的导数求速度，速度对时间的导数求加速度。

以绳拉物体运动问题为例。在离水面高度为h的岸边，有人用绳子拉船靠岸，人以v0的速率收绳。试求船在离岸边s距离时的速率和加速度。

分析：建立绳拉物体运动坐标系，坐标系如图1所示。运动的分解是难点，人拉绳的速度和船前进的速度之间的关系学生容易混淆，而运用导数知识很容易求解。

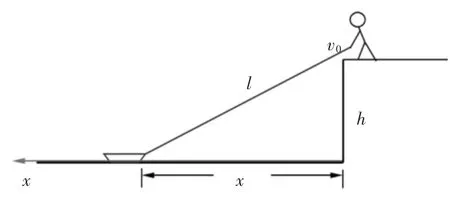
图1　绳拉物体运动示意图

由l2=x2+h2，此式两边对时间求导得：

2　微分方法

微积分包含变与不变的辩证关系、整体与局部的关系（化整为零）及量变到质变的关系（求和-积分）［1-4］。把复杂的物理问题进行无限分割，使局部范围无限小，即微分；把所有无限多个微元的结果求和，即积分。

微分就是利用微元法处理较复杂的物理问题。把整体分成许多微小部分，变量看作常量进行处理，使问题简单化。如变力做功，首先把路径分成许多微元d，这些微元上质点所受的力可视为恒力，在每一段位移上力所做的元功可由算出，然后对所有元功求和得到沿整段曲线力对质点做的功。

例如，在刚体力学中，求质量为m、半径为R的均匀圆盘绕与盘面垂直并通过盘心的轴的转动惯量，如图2所示。

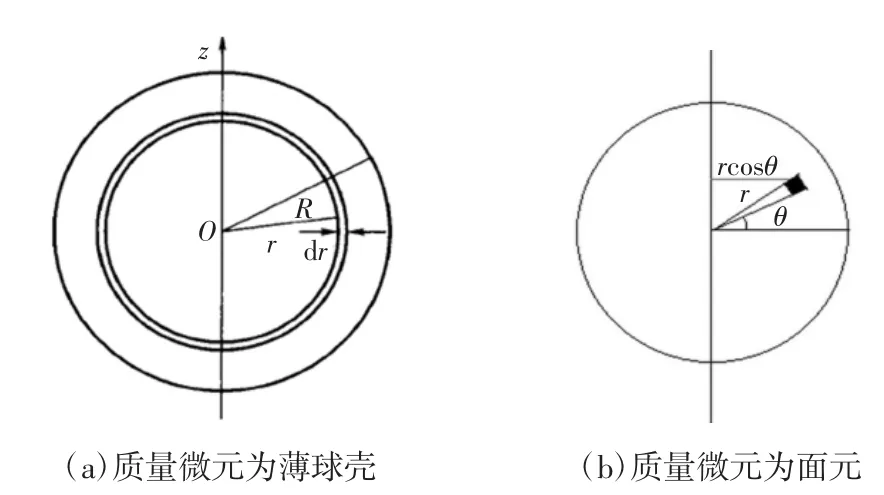
图2　质量微元的选取

分析：圆盘可看做连续分布的质点系，求解其转动惯量，要利用单个质点或已知模型对某一轴的转动惯量表达式，因此对连续体先选取微小质量单元dm，然后再积分（质点系求和），关键在于选取合适的微元并写出其表达式。为使计算简单，将圆盘视为由许多薄圆环组成，取一半径为r、宽度为dr的薄圆环作为微元，如图2（a）所示。薄圆环的质量记为dm；圆盘的密度为σ，σ=m/πR2。有dm=σds=m/πR22πrdr=2m/R2rdr，则该薄圆环绕盘心轴的转动惯量为：

将所有质量微元dm对该转轴的转动惯量dJ进行积分计算可得问题的解，即：

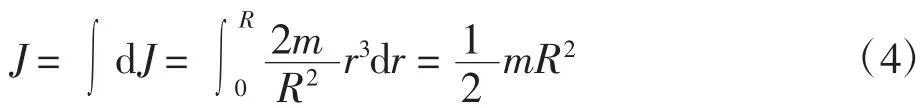
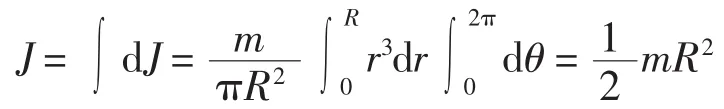
应用微分处理物理问题时，本质上是处理物理量间“变”与“不变”的对立关系。本题中，组成圆盘整体的质点系与轴间相对位置并非恒定，因此直接利用质点对轴的转动惯量公式无法求解。但对于质量微元而言，可以认为质量微元对轴的距离是不变的，其转动惯量可以直接利用质点转动惯量表达式表示。微元的选取并不唯一，应遵循便于问题分析和计算的原则，选取不同微元，其结果都是相同的。

3　积分方法

积分与微分互为逆运算，积分即对微分进行求和。积分路径和积分上下限的选择既要符合客观规律，又要尽量简单以减少计算量。积分方法在力学、电学等许多问题中有着广泛的应用。如在求解变力做功时，要先判断是保守力还是非保守力做功，若为保守力做功，因保守力做功与路径无关，故可选择最简便的积分路径。当积分区域具有对称性时，可利用其对称性缩小积分范围，减少计算量。在解决定积分、含积分的极限等问题时，应用积分中值定理可使复杂的问题简单化。

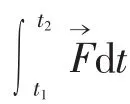
得到动量定理

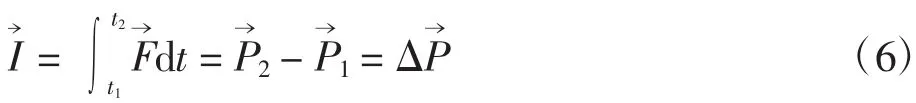
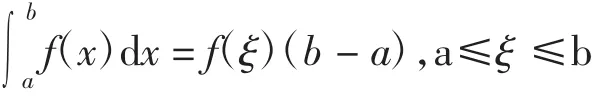
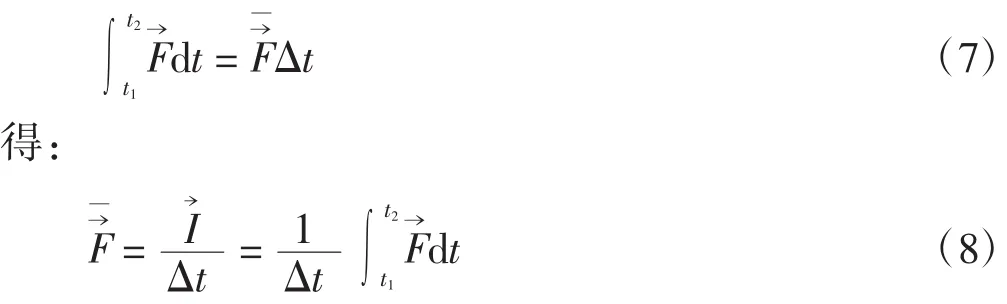
运用积分运算的定义、特点和性质时，需要结合物理问题的不同特点，选择不同的处理方法。需要注意的是，在处理物理问题时要结合问题的实际意义分析结论的可取性。

4　微分方程方法

微分方程是表示未知函数的导数以及自变量之间关系的方程，其应用十分广泛。力学、天文学、量子力学等领域的许多问题都可以用微分方程来求解。微分方程在物理学中的重要应用，在于求得满足一定边界条件的解。如谐振子模型可以解决许多量子力学中的实际问题，固体中原子的振动问题就可以利用该模型研究［5］。通过求解一定边界条件下的常微分方程，可以得到谐振子的能量本征值。

假设一维谐振子的势能函数为：

质量为m、频率为ω的振子的哈密顿量可表示为：

一维谐振子的定态薛定谔方程为：

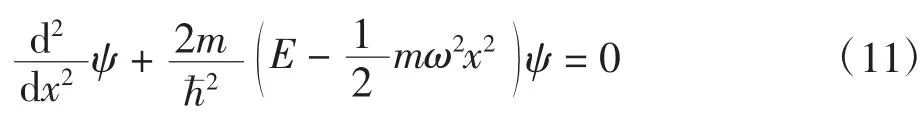
为简化求解，引入

上式为一个变系数二阶常微分方程。求解此方程，并使波函数满足单值、有限和连续的束缚条件，就可得谐振子的能量本征值。

当|y|→∞时，上式中λ可忽略，写为：

设波函数的解为：

上式代入薛定谔方程可得：

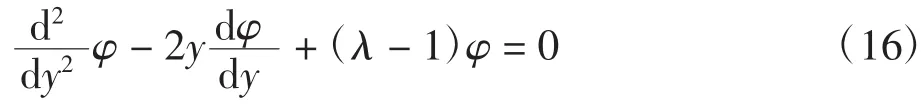
应用级数法，把φ展开成y的函数。该级数必须只含有限项，才能在|y|→∞时使φ（y）有限，即λ为奇数，λ=2n+1，（n=0，1，2，…），得谐振子的能量值为：

再有就是要加强对教师自身的安全知识培训与学习，加强自身素质的提高也很有必要。如：经常性地开设各种法制、心理健康等安全知识专题讲座，不定期开展安全知识竞赛等活动，加强对各种常见安全事件发生的防范措施和应急处理方法等所进行的讲解和示范，切实把安全管理与安全教育有机地结合起来很有必要。

微分方程建立了变量导数与变化量间的关系式。它不仅是各物理参量间的方程，而且也是物理量变化率的方程式。因此，理解并掌握微分方程对大学物理学习至关重要。

5　近似计算法

近似法是一种常用的解题方法，在解决物理问题时广泛使用。如物理模型的近似是指研究物体运动时，将研究对象近似为有质量但不考虑体积或形状的质点。其他如刚体、点电荷、理想气体等也都是采用了一定程度近似的理想化模型。在物理规律的推导及相关问题求解中，也经常需要结合数学知识进行近似处理，如利用泰勒级数，忽略高阶小量，可得函数的近似解，很多物理定律都是相应泰勒级数展开式一阶项下的线性近似结果［6-7］。上文中提到的简谐振动往往可作为复杂运动的初步近似，如双原子分子中两原子间的势V是二者相对距离x的函数，如图3所示。

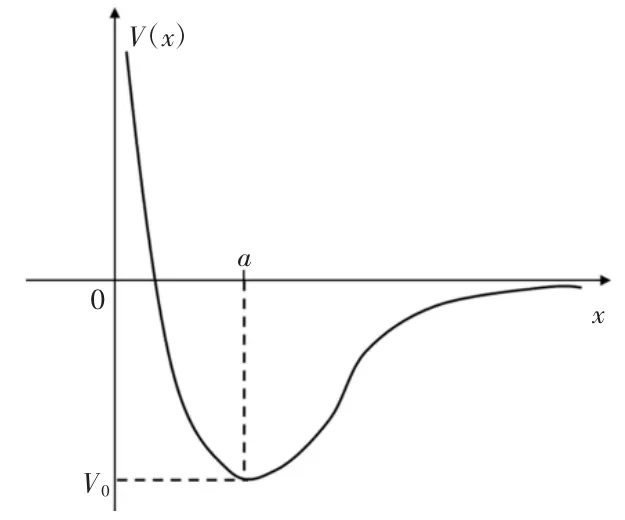
图3　双原子分子两原子间的势函数V（x）

在x=a处，V有一极小值V0。在平衡态x=a附近势能可以展开成泰勒级数多项式：

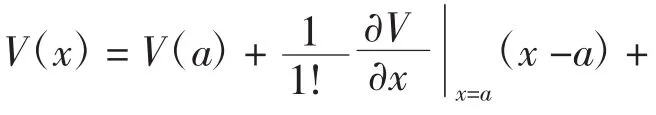
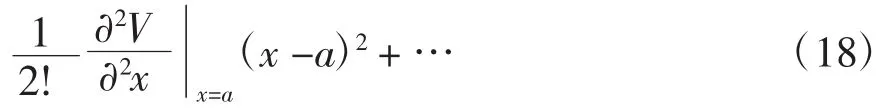
式（18）精确到二级近似，可写为：

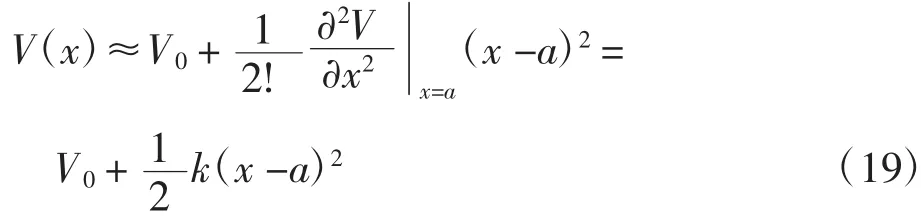
取新坐标原点为（a，V0），则势能可表示为标准谐振子势能形式：

式（20）容易精确求解。一些复杂势场中粒子的运动可以用线性谐振动来近似描述，这种处理方法在物理中有着广泛应用。

在电磁学部分公式及定律的推导中也会利用泰勒级数进行近似处理［7］。例如，2个完全相同且彼此平行的线圈，其电流的流向相同，如图4所示。

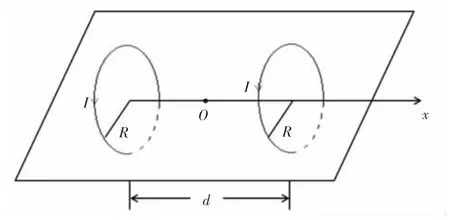
图4　两圆电流线圈示意图

求证当2线圈中心间距d等于线圈半径R时，在2线圈中心连线的中点O附近区域，磁场可看成是均匀磁场。

分析：建立如图4所示的坐标系，设磁感应强度在Ox轴线上的分布为B（x），如果在轴线上某点处dB/dx=0，同时满足d2B/dx2=0，该点附近区域为均匀磁场。

证明：在x轴上任一点的磁感强度为2个电流线圈在轴线上磁感应强度的叠加，

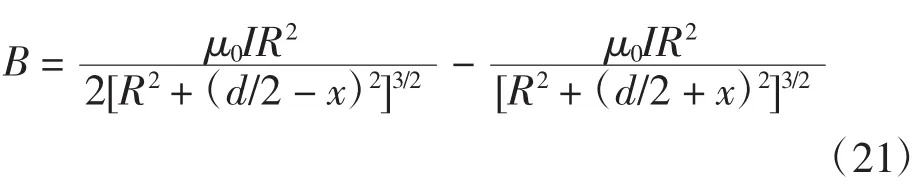
当dB/dx=0和d2B/dx2=0时，磁感强度在该点附近区域内是均匀的。

利用泰勒级数将磁感应强度B（x）在2线圈中点O附近展开，得：

在上述证明过程中，利用泰勒级数展开近似求得2线圈中点附近区域为均匀磁场，同时运用了数学中的极值法。

6　结束语

本文通过一些实例分析了微积分中微分、积分、导数、微分方程以及近似等方法在大学物理学习中的应用。本研究旨在对学生的大学物理学习有一定的指导作用，为学生应用微积分知识研究、分析和解决物理问题提供解题思路和有效方法。

［1］黎定国，邓玲娜，刘义保，等.大学物理中微积分思想和方法教学浅谈［J］.大学物理，2005，24（12）：51-54.

［2］阳喜元，蒋彬.有关大学物理微积分应用的若干问题［J］.物理通报，2011（6）：13-16.

［3］马新泽.浅析大学物理中的微积分教学［J］.昌吉学院学报，2009（2）：111-114.

［4］曹剑英.微积分在大学物理教学中的应用研究［J］.赤峰学院学报：自然科学版，2013，29（5）：13-14.

［5］张三慧.大学物理学下册［M］.3版.北京：清华大学出版社，2011.

［6］邢永丽，陈建春.泰勒级数在近似计算中的应用［J］.湘潭师范学院学报：自然科学版，2004，26（1）：5-8.

［7］马文蔚.物理学系题分析与解答［M］.5版.北京：高等教育出版社，2006.

Application of calculus in university physics

WANG Jin-hua
（School of Science，Tianjin University of Technology and Education，Tianjin 300222，China）

Based on some specific examples，the application of differential，derivative，integral，differential equation，approximation is analyzed in university physics.The analysis provides useful reflections on researching，analyzing and solving physical problems for students，and meanwhile promotes the learning of university physics.

university physics；calculus；differential equation；approximate method；derivative

O172

A

2095－0926（2015）04－0050－04

2015-07-07

王金华（1981—），女，讲师，博士，研究方向为物理教学及材料物理.