波概念迭代算法原理分析

姬五胜，张玉

（1.天津职业技术师范大学天线与微波技术研究所，天津300222；2.深圳信维通信股份有限公司上海分公司，上海201315）

波概念迭代算法原理分析

姬五胜1，张玉2

（1.天津职业技术师范大学天线与微波技术研究所，天津300222；2.深圳信维通信股份有限公司上海分公司，上海201315）

介绍了波概念迭代算法（WCIP）基本计算流程，从波概念的形成、迭代技术和横波技术等方面剖析了算法原理，提出该算法具有计算复杂度低、计算时间短、所需内存小等优点，也指出了该算法存在的问题及局限性。基于该算法，利用Matlab语言编程仿真了一个发夹型滤波器的散射参数以及电路表面切向电场、切向电流密度分布，并验证了算法的可行性和正确性。

WCIP原理；迭代技术；计算效率；发夹滤波器

电磁场的数值计算可为微波电路的建模和设计提供高效准确的分析。目前，已经有诸多数值计算方法分析单片微波集成电路（monolithic microwave integrated circuit，MMIC）和平面结构。当前应用较多的数值计算方法主要有2大类：一类是以电磁场问题的积分方程为基础的数值方法，如矩量法系列；另一类以电磁场问题微分方程为基础的数值方法，如有限差分法系列。基于变分原理的有限元法可以归为微分方程法，也可以用矩量法的语言来描述［1］。这些算法存在着原理复杂、计算时间长、存储容量大等缺点。

1996年，Azizi和Baudrand等［2］提出了波概念迭代方法（wave concept iterative procedure，WCIP）。此后，很多学者在激励源建模、电路等效、不均匀网格划分等问题上对该方法展开了较为深入的研究，其应用范围也日趋广泛，包括：天线、滤波器、频率选择表面、平面多层结构、分形结构、柱状问题等［3-5］。Ayari等［6］基于该方法开发了一款电磁分析软件。相比而言，国内研究进展缓慢，对该算法未给予足够重视。

本文简要介绍WCIP算法的基本原理，从传输线方程的解、边界条件、谱域传输线理论等方面分析该算法的3个关键技术；结合算法原理详细讨论该算法的优缺点及局限性；最后以一个发夹滤波器为例，应用Matlab编程仿真该滤波器电路表面切向电场、切向电流密度分布，计算其散射参数，并与参考文献结果进行比较，验证了该算法的正确性、可行性和高效性。

1　WCIP算法基本原理

根据希尔伯特空间变换，利用电路不连续性表面的切向电场ET和电流JT引入波概念方程为：

式中：Ai为电路表面的入射波；Bi为电路表面的反射波；Z0i为介质i（i=1，2）的特征阻抗，其值为Z0i=。WCIP算法电路模型如图1所示［7］。

图1　WCIP算法电路模型

在空域中，微波电路不连续表面按其属性可划分成金属区域、介质区域和源区域。

根据各区域的边界条件，计算出整个区域的散射矩阵。边界条件为：

将式（2）～式（4）代入式（1），得到空域散射矩阵为：

在电路表面，空域入射波和空域散射波之间的关系为：

波从电路表面传播到上下介质区域，为使用传输线理论计算波的反射情况，将波从空域转化为模式域。FMT表示空域向模式域转换，IFMT则反之。

FMT、IFMT的计算式为：

模式域中，入射波和反射波的谱域反射关系为：

式中：m、n表示模式数；α=TE，TM；Yαmn，i代表介质区域i中第mn阶模式的导纳，表示为：

WCIP算法计算流程如图2所示。

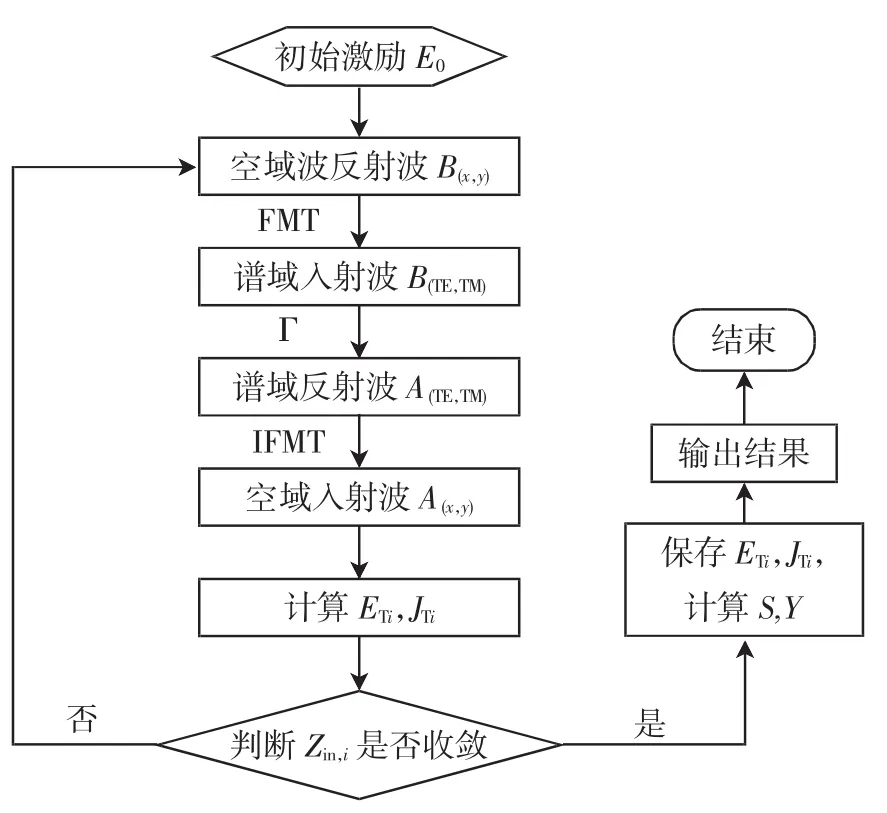
图2　WCIP算法计算流程

每次迭代之后计算输入阻抗Zin，计算公式如式

（12），迭代到Zin收敛为止。l、w为介质基片的长和宽。

2　WCIP算法的关键技术

2.1波概念的形成——由场到波

波概念是该方法的理论创新之处，也是最关键之处。下面从波动方程的解来引入波概念。

波动方程的通解为：

磁场和电流密度的关系为：

式（15）中：A1e-jkz为入射波，记为A；A2ejkz为反射波，记为B。由（15）式得：

此式实现了用切向电场和切向电流表示入射波和反射波，波概念由此产生。

2.2迭代技术

迭代是一种逐次逼近法，迭代的前提是问题本身能够收敛，对WCIP算法而言是波的运动状态趋于稳定。WCIP算法的迭代过程也是波的传输过程，通过波在空域和模式域的不断转换来求解场分布，避免了大矩阵的求逆运算，降低了存储空间，缩短了计算时间。

迭代初始时，在分界面上放置沿x方向极化的激励源E0，它在上下区域产生2项波B01（x，y）和B02（x，y），它们分别向空气和介质中传播。由于空气层、介质层的特性阻抗与电路层的特性阻抗不相同，在上下层会出现反射。反射波又回到电路表面，完成一次迭代，迭代过程如图2所示。

迭代过程建立在空域波和模式域波互相转化的基础上。为缩短转化时间，引入3种不同的基底：笛卡尔基底（CB）、傅里叶基底（FB）和模式基底（MB）［8］。笛卡尔基底应用在电路表面，用于电路建模及计算电路表面散射系数；傅里叶基底作为空域和模式域的过渡，将空域波利用傅里叶变换为谱域波；模式域基底用来将波表示成本征模叠加模式，以方便使用谱域反射系数对各模式进行处理。

2.3横波技术

从广义传输线角度考虑，波在导波系统的传输方向具有共性，包括入射波和反射波；而在导波系统的横向具有个性，不同的横截面具有不同的边界条件，这就决定了不同的本征模。所以，在波概念的推导中，不考虑波传播的方向因子e-jkz和ejkz，这就简化了求解过程。

WCIP算法基于横波而不是切向电场，可以方便地利用散射算子，而不用操作阻抗或导纳算子。散射算子描述入射波和反射波之间的关系，可用横波描述；阻抗或导纳算子描述广义电压和电流之间的关系，用切向电磁场描述。WCIP算法的优势是避免求解复杂的微积分方程，而用简单的代数方程代替。横波建立在波概念基础上，跳出了在电路表面求解电磁场问题的定式，而在垂直于电路表面的方向，利用波的空域散射和谱域反射理论求解电场和电流密度分布。

另外，根据谐振腔理论提出了与矩形波导相类似的模式基底［9］。传输模式的确定也可参照矩形波导截止频率公式计算，如式（17）。传输模式的确定，关系到导纳和模式反射系数的计算，可参考文献［10］。

3　WCIP算法的优点及局限性

3.1算法原理简单，物理意义清晰

WCIP算法涉及的计算分为空域和模式域2部分。空域计算主要包括空域散射，如式（6）。其中，A、B、S都是m×n维矩阵；m、n为划分网格的维数。谱域主要包括谱域反射，如式（9）。空域到模式域的转化经过2个步骤：①利用FFT2先将空域转换为谱域；②用模式转换矩阵P将谱域转换成模式域。算法整个过程物理意义清晰，计算只涉及矩阵乘法和加法，利用Matlab语言编程可轻松实现。

3.2计算复杂度低、效率高，存储容量小

设NT为电路模型的总网格数，n为迭代次数，K为电路表面金属部分占总面积的百分比。对于WCIP，空域、谱域的计算复杂度均为NT；FMT的正、反变换计算复杂度均为2NTln NT。由于迭代一次要进行1次空域计算、2次谱域计算、FMT和IFMT各1次，所以1次完整的WCIP迭代计算复杂度为3NT+4NTln NT，总的计算复杂度为n（3NT+4NTln NT）；而MOM的计算复杂度为（KNT）3/3；FEM的计算复杂度为2NT3/3。由此可以看出，矩量法的计算复杂度最高，而WCIP的计算复杂度最低。计算过程中，只需为变量开辟第1次迭代时的空间，以后各次迭代结果都存储在上一次的空间中，以代替原来的结果，这对节约CPU的存储空间十分有利。在模式变换过程中，利用快速FFT算法，进一步加快了计算速度。

3.3电路描述简单

任何形状的电路都能用海维赛德函数表示，如式（5）。这种方式实际上就是用0和1构成的矩阵将电路拓扑形状数字化。用矩阵表征电路几何形状的前提是对电路整体进行矩形网格划分。为了能够使用FFT快速算法，网格划分m×n中的m、n最好是2的指数形式。网格划分的最小单位必须小于或等于电路中最小的几何尺度。本算法网格划分与有限元法的最大不同之处在于前者是在电路平面上，利用矩形网格划分；后者则是在三维电路上，利用四面体对整个体积进行划分。显然WCIP的网格划分比有限元法简单且节省空间。此外，使用非均匀网格划分技术后，WCIP算法的计算速度也有显著提高［4］。

WCIP算法在应用过程中，受电路结构和传输模式的限制。WCIP算法假设层与层之间的介质是均匀的，这样可应用广义传输线理论的一些基本结论。但是当层与层之间存在通孔或其他垂直结构时，波的传播方向上会存在径向波或其他复杂波，不能简单地用传输线理论来等效。目前该算法主要应用在单层平面电路或多层均匀介质平面电路。WCIP算法属于电路分析算法，计算中只考虑传输主模；但实际中传输模式往往有多个，故该算法仿真结果与其他数值算法的结果存在一定误差。

4　仿真计算

用WCIP算法分析一种发夹滤波器［11］，基底材料为r-Al2O3（相对介电常数10.05），其拓扑结构如图3所示，其他参数如表1所示。

图3　发夹滤波器的拓扑结构（单位/mm）

表1　发夹滤波器的其他参数

在计算中，利用Matlab建立发夹滤波器部分模型，网格数为128×128。计算得到电路表面切向电场分布和电流密度分布分别如图4和图5所示；S参数与原始文献的结果对比如图6所示。

图4　发夹滤波器电路表面切向电场分布

从图中可以看出，WCIP所得S参数曲线形状与原始文献结果大致吻合，中心频率有一定的偏移。一方面是因为WCIP算法只用主模计算，另一方面是因为原始文献中未给出介质基片的尺寸。本文根据传输线匹配等原则假设介质区域的长和宽，因此可能存在差异。在主频为2 GHz、内存为2 GB的计算条件下，仿真计算时间不到1 min，而采用基于FEM的Ansoft HFSS软件对同一电路的仿真时间约需4 min。因此，相对于FEM，WCIP具有较高的计算速度。

图5　发夹滤波器电路表面电流密度分布

图6　WCIP计算发夹滤波器参数

5　结束语

本文介绍了WCIP算法的原理及关键技术，并提出该算法对电路的描述方式简单，对激励端口的处理方便；整个分析过程物理意义明晰，算法原理简单，计算容易实现；计算复杂度低、存储容量小，计算时间短。但WCIP算法对电路结构和模式选取有一定的限制，故其应用范围和计算精度受到限制。

［1］王秉中.计算电磁学［M］.北京：科学出版社，2002.

［2］AZIZI M，BOUSSOUIS M，AUBERT H，et al.A three-dimensional analysis of planar discontinuities by an iterative method［J］.MicrowaveandOpticalTechnology Letters，1996，13（6）：372-376.

［3］BRAHIM T I E，ZAIRI H，GHARSALLAH A，et al.Analysis of an EBG filter using an iterative method［C］//2008 2nd International Conference on Signals，Circuit and Systems. Monastir：IEEE，2008：1-4.

［4］TITAOUINE M，RAVEU N，NETO A G.Dual-band and enhanced band FSS characterization using WCIP method［J］. Microwave and Optical Technology Letters，2010，52（4）：836-839.

［5］SBOUI N，LATRACH L，GHARSALLAH A，et al.A 2D design and modeling of micro strip structures on inhomogeneous substrate［J］.International Journal of RF and Microwave Computer-Aided Engineering，2009，19（3）：346-353.

［6］AYARI M，AGUILI T，BAUDRAND H.An extended version of the differential-integral approach based on the transverse wave formulation［C］//2006 6th International Conference on ITS Telecommunications Proceedings.Chengdu：IEEE，2006：457-460.

［7］JI W S，LUO Q Z，YANG F.Analysis of H-shaped patch antenna by wave concept iterative procedure［C］//2010 International Conference on Microwave and Millimeter Wave Technology.Chengdu：IEEE，2010：797-800.

［8］AYARI M，AGUILI T，BAUDRAND H.More efficiency of transversewaveapproach（TWA）byapplyinganisotropicmesh technique（AMT）for full-wave analysis of microwave planar structures［J］.Progress in Electromagnetic Research B，2009，14：383-405.

［9］TITAOUINE M，NETO A G，BAUDRAND H，et al.Analysis of frequency selective surface on isotropic/anisotropic layers using WCIP method［J］.ETRI Journal，2007，29（1）：36-44.

［10］TITAOUINE M，NETO A G，BAUDRAND H，et al.WCIP method applied to active frequency selective surfaces［J］. Journal ofMicrowave and Optoelectronics，2007，6（1）：1-16.

［11］SEKIYA N，NAKAGAWA Y，SAITO A，et al.Novel trimming technique for tunable HTS microstrip filters［J］.Physica C Superconductivity，2008（15/16/17/18/19/20）：1958-1961.

Analysis of wave concept iterative process

JI Wu-sheng1，ZHANG Yu2
（1.Institute of Antenna and Microwave Techniques，Tianjin University of Technology and Education，Tianjin 300222，China；2.Shanghai Center of Shenzhen Sunway Communication Co Ltd，Shanghai 201315，China）

The elementary procedures of Wave Concept Iterative Process（WCIP）are briefly introduced in this paper，and the principle of algorithm is analyzed with respect to the formation of wave concept，the technique of iterative process and the technique of transverse wave.The advantages of lower complexity，shorter computing time and lower memory cost are also discussed in detail，while the disadvantages of the algorithm and limitations of application are pointed out.Based on the algorithm，scattering parameters，tangential electrical field on the circuit surface and tangential current density distribution of a hairpin filter are simulated through Matlab language programming，which verifies the correctness and feasibility of the method.

WCIP principle；iterative technique；computing efficiency；hairpin filter

TN713；TP301.6

A

2095－0926（2015）04－0010－05

2015-07-23

甘肃省高等学校研究生导师科研计划项目（0811-05）；天津职业技术师范大学预研基金项目（KJY14-05）.

姬五胜（1968—），男，教授，博士，研究生导师，研究方向为微波电路三维集成、无线电技术与信息系统和计算电磁学.