五轴数控机床旋转轴几何误差辨识新方法

付国强,傅建中,沈洪壵

（浙江大学流体动力与机电系统国家重点实验室,浙江杭州310027）

五轴数控机床旋转轴几何误差辨识新方法

付国强,傅建中,沈洪壵

（浙江大学流体动力与机电系统国家重点实验室,浙江杭州310027）

为了系统、快速方便地测量五轴数控机床2个旋转轴所有的几何误差项,提出一种基于球杆仪测量的六圈法几何误差辨识方法.基于五轴数控机床几何误差模型分析旋转轴几何误差项对机床综合几何误差的影响,与平动轴9线法辨识原理比较,并结合球杆仪测量的特点,建立六圈法辨识方法.该方法根据旋转轴各个几何误差项的性质可辨识得到每个旋转轴包括垂直度误差和安装误差的全部10项几何误差.为了提高六圈法辨识精度,分析球杆仪安装误差对测量数据的影响,并用最小二乘法得到球杆仪安装误差,从测量数据中剔除安装误差的影响,仿真结果验证了消除安装误差方法的正确性.采用六圈法测量辨识机床旋转轴误差,并比较补偿旋转轴误差前后的测量数据,补偿后误差降低了50%到80%,实验结果表明,六圈法辨识精度高,系统性好,可以测量不同的旋转轴.

六圈法；球杆仪；旋转轴；几何误差；安装误差

随着加工精度要求的提升,五轴数控机床在制造业中所占的比例越来越大.机床的加工精度是衡量一个机床的重要标准.影响五轴数控机床精度的因素包括几何误差、热误差、切削力误差、振动误差等,其中几何误差和热误差占60%左右［1］.几何误差重复性好,在长时间内稳定不变,所以易实现几何误差的建模和补偿来提高机床的加工精度［2］.

数控机床几何误差模型大多基于多体理论建立［3］,指数积理论也可建立几何误差模型［4］.模型可预测和补偿机床的几何误差,前提是测量辨识得到模型中的各个基本几何误差项.三轴机床的21项几何误差的辨识方法比较成熟,包括基于激光干涉仪的9线法［14］,12线法,体对角线分步法［15］等,其中9线法测量线数少,测量方便,系统性好,且无原理误差,适合不同的三轴数控机床.对于五轴数控机床旋转轴误差的测量国内外也出现了很多装置,包括3D探头［5］,球杆仪,R-test等［6］.基于球杆仪测量的误差辨识方法很多,Zargarbashi等［7］提出了基于球杆仪的5种测试阶段来辨识机床A轴的几何误差,只需A轴单独旋转运动.Tsutsumi等［8］采用三轴同步运动将球杆仪分别置于旋转轴的轴向、径向和切向3个位置来辨识旋转轴几何误差.Tsutsumi等［9］又提出了四轴同步运动的方法.Tsutsumi等［10］在三轴同步运动测量的基础上用球杆仪分别在圆柱坐标系和笛卡尔坐标系下进行测量,分析了球杆仪安装误差对这2种辨识方法结果的影响.Lee等［11］将C轴几何误差用参数化形式表示,然后结合5种测试路径来辨识旋转轴的几何误差项.Lee等［12-13］用球杆仪辨识旋转轴的垂直误差和位置误差,对误差辨识精度进行不确定分析.这些方法为更好的旋转轴几何误差辨识方法奠定了基础.但是这些方法只能得到旋转轴的某几项误差项,且不能同时测量五轴数控机床的2个旋转轴的几何误差.另外也没有如9线法这种测量方便,与机床误差模型无关的适合于不同旋转轴的辨识方法.

针对这些问题,本文提出一种基于球杆仪测量的六圈（six circle）几何误差辨识方法.首先分析旋转轴几何误差对机床精度的影响,其次利用各个几何误差项的性质,得到每个旋转轴的10项几何误差.然后分析球杆仪安装误差对六圈法中球杆仪轨迹的影响,并采用最小二乘法来消除安装误差.采用仿真分析来验证安装误差分离方法的正确性.最后采用六圈法测量辨识机床旋转轴几何误差来验证其有效性和正确性.

1 五轴数控机床几何误差模型

1.1 五轴数控机床几何误差建模

几何误差是影响五轴数控机床精度的主要因素之一,几何误差模型多是基于多体理论采用D-H齐次矩阵的形式表示的.以CAFYXZ型双转台五轴数控机床为例,

简述五轴数控机床几何误差建模方法.如图1所示为该机床结构简图.五轴数控机床可视为由2个开环运动链组成：工件链和刀具链.该机床工件链为床身—A轴—C轴—工作台；刀具链为床身—Y轴—X轴—Z轴.

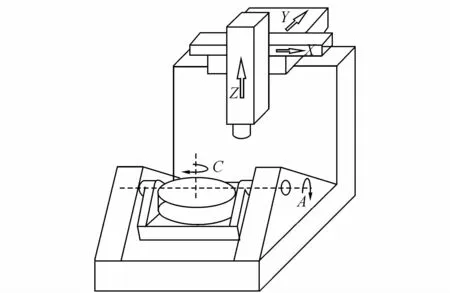
图1 CAFYXZ型双转台五轴数控机床示意图Fig.1 Structure of CAFYXZ type five-axis machine tool

采用D-H几何误差建模方法,对于工件链,工作台上工件在参考坐标系（床身）下的齐次变换矩阵可表示为

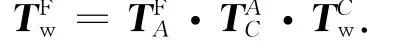
对于刀具链,刀具上刀尖相对于床身的齐次变换矩阵为

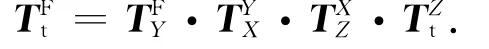
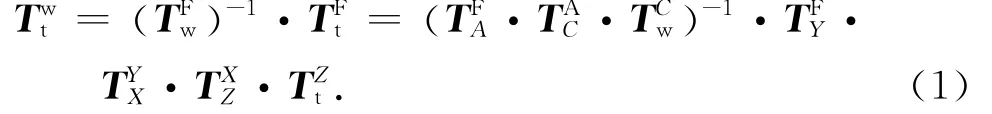
在实际情况中,由于装配、制造等一系列的原因,使得相邻部件之间存在几何误差,那么部件之间的齐次变换矩阵就应包括误差齐次矩阵,则实际的齐次变换矩阵应表示为

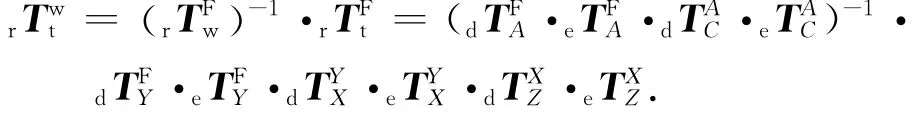
则五轴数控机床刀具相对于工作台的综合几何误差可表示为

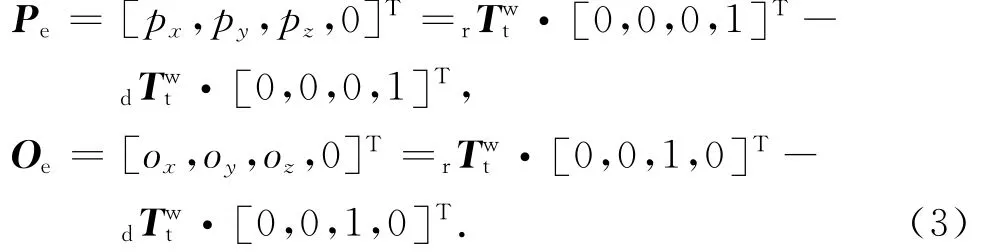
式中：Pe为刀具相对于工作台的位置误差,Oe为姿态误差.

1.2 旋转轴几何误差项

相对于三轴数控机床,五轴数控机床的旋转轴会给机床带来额外的几何误差项.因为每个物体存在6个自由度,那么每个物体存在6个误差源.与平动轴一样,每个旋转轴有6项基本误差项,包括3项线性误差和3个转角误差.如图2所示描述了C轴的6项基本误差项.δxc、δyc、δzc分别是x,y,z方向的线性误差,εxc、εyc和εzc分别表示绕x,y,z轴的转角误差.同时由于安装等原因,C轴旋转轴线与X轴和Y轴之间存在角度和位置偏差,即垂直度误差和位置误差.C轴存在2项垂直度误差,分别为Scx和Scy,同时存在2项位置误差为ocx和ocy.那么C轴共存在10项几何误差项.则C轴的误差齐次矩阵可表示为［16］

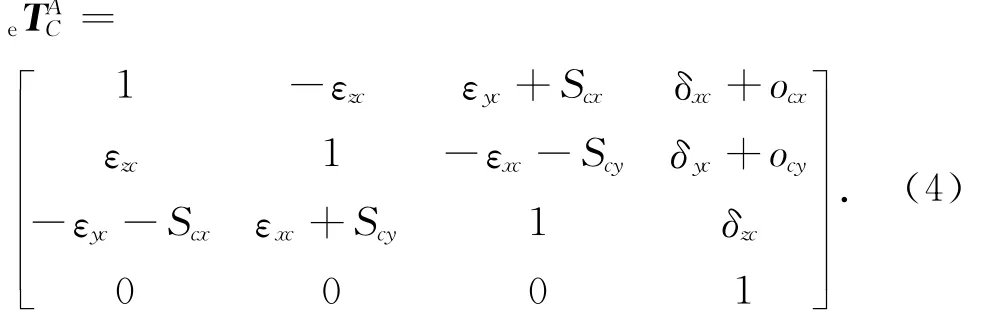
同理,对于A轴,3项线性误差为x方向的δxa,y方向的δya和z方向的δza,3项转角误差为绕x轴旋转的εxa,绕y轴旋转的εya和绕Z轴旋转的εza,2项垂直度误差为与Y轴之间的Say和与Z轴之间的Saz, 2项位置误差为y方向的oay和z方向的oaz.A轴的误差齐次矩阵为

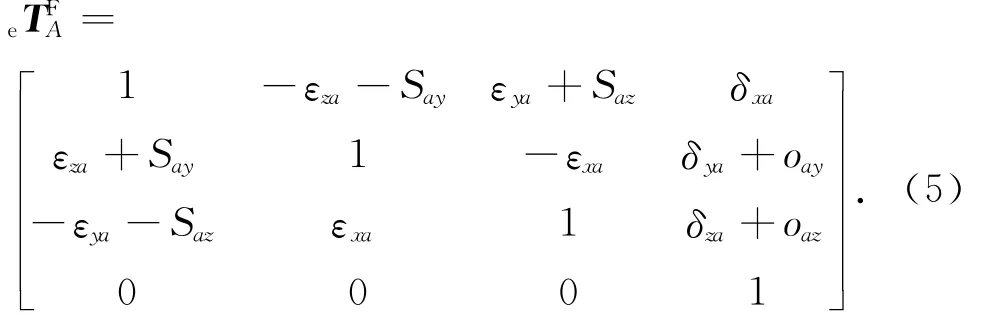
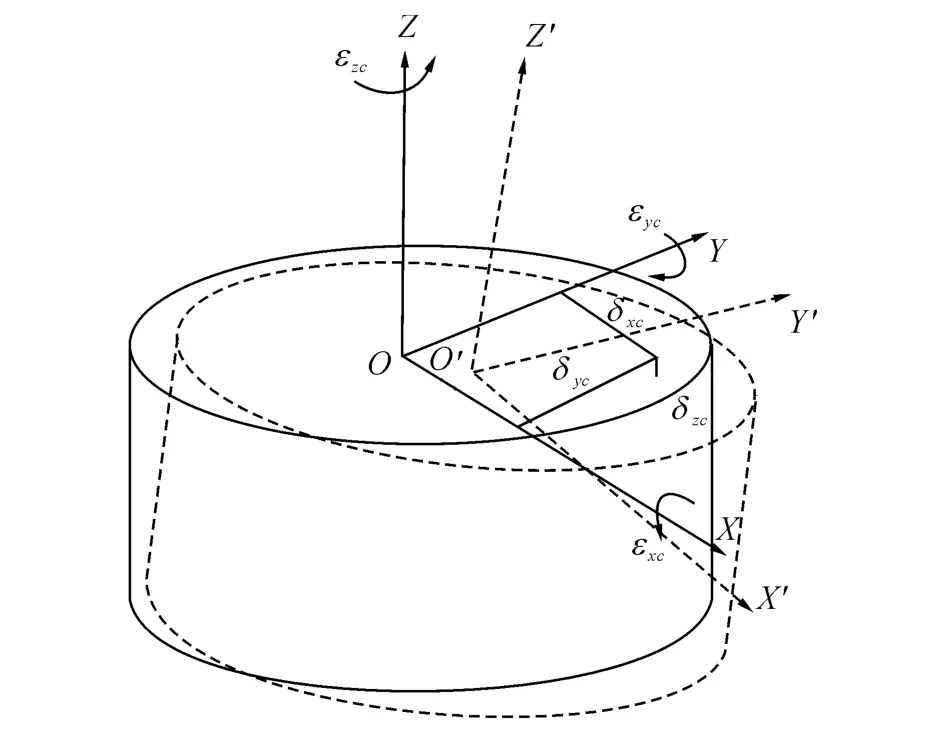
图2 C轴6项基本几何误差示意图Fig.2 Six basic geometric error components of C-axis

2 基于球杆仪的旋转轴误差测量方法

2.1 基于球杆仪的六圈法

五轴数控机床共存在41项基本误差项,其中3个平动轴的21项几何误差项的辨识方法比较成熟.对于旋转轴几何误差项的测量仍需要一种系统的、准确的辨识方法.首先根据上转轴误差项的定义可以得知,各个轴的基本误差项是相对于本身坐标系进行测量,同时在建模过程中式（2）是根据“左基右一”的原则得到各个轴实际的齐次转换矩阵,进一步说明各个轴的几何误差项是相对于轴本身坐标系测量的,而不是相对于整个机床的参考坐标系测量得到的.那么旋转轴基本几何误差项应在旋转轴自身坐标系下进行测量辨识,这就要求测量装置在测量时相对于旋转轴坐标系静止不动,或者将测量数据根据坐标变换转换到旋转轴坐标系下进行辨识.而球杆仪测量时本身轨迹是圆或者圆弧,那么球杆仪测量旋转轴时就具有一定的优势,可以选择它辨识旋转轴误差,同时还通过球杆仪的安装,或者机床RTCP功能等,保证球杆仪在旋转轴本身坐标系下测量方向不动.

对于双转台五轴机床,工作台安装在C轴上,则机床几何误差模型表示了在C轴坐标系下的综合误差.为了测量方便,在测量C轴几何误差项时,保持A轴静止.假设在初始状态下,即在C轴转角为0时,刀具在C轴坐标下的坐标为［xo,yo,zo］,那么当C轴旋转一定角度γ后,为了保证刀具在C轴坐标下的坐标不变,即

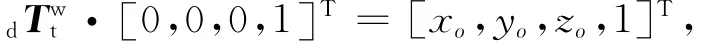
则可得到3个平动轴相应的进给量为

则根据式（3）和（4）可以得到C轴运动γ角度后的各个方向的综合误差为

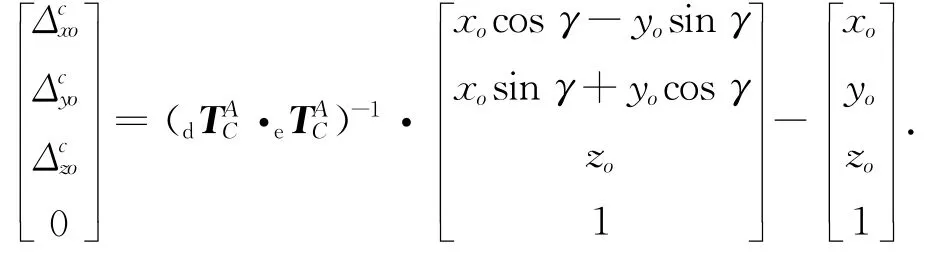
为了辨识方便,只探索C轴误差对综合几何误差的影响,经过整理得到

用同样的方法可以得到A轴旋转轴误差对机床精度的影响,首先得到A轴旋转一定角度后,平动轴进给量为

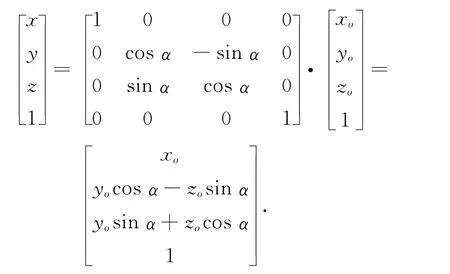
则根据式（3）和（5）可以得到A轴运动α角度后的综合几何误差：

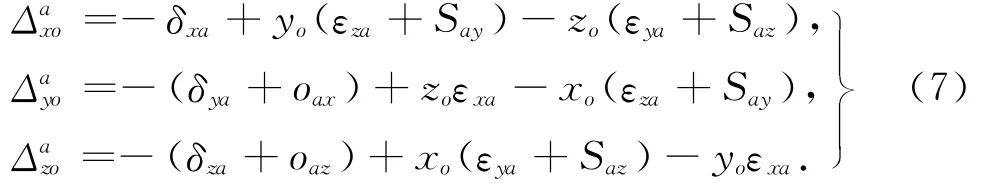
不考虑旋转轴垂直度误差和位置误差时,式（6）和（7）与平动轴几何误差辨识方法9线法辨识原理一致.9线法中每3条线可以辨识得到一个轴的6项基本几何误差项,该方法要求双频激光干涉仪可以测量定位误差和2个方向上的直线度误差,对测量仪器要求较高,也是因为该仪器可以一次性测量得到不同方向的误差,所以只需3条线即可辨识一个轴的6项基本误差项.而球杆仪本身只能测量一个方向的定位误差,那么就至少需要6次不同的测量来辨识一个旋转轴的6项基本误差.本文就提出了基于球杆仪的“六圈法”来辨识旋转轴几何误差项.

“六圈法”是球杆仪在6个不同的位置处跟随测量旋转轴同步转动一圈来测量辨识旋转轴几何误差项的测量方法.对于C轴,根据机床联动功能保证球杆仪与C轴同步转动.先不考虑垂直度误差和位置误差的影响,即可先将垂直度误差视为相应的转角误差的一部分,位置位差作为相应线性误差的一部分,那么式（6）变为

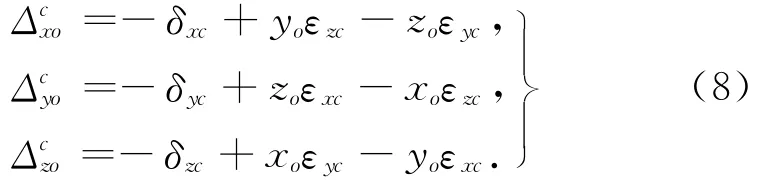
式（8）与9线法中的辨识原理［14］是一样的,其本身与机床误差模型无关,可以根据各个误差的定义和坐标系变换直接得到,只要式中xo,yo,zo选择合适的值就可以辨识得到这6项误差.六圈法中球杆仪的6个位置如图3所示,其中位置1,4,5处球杆仪的方向与被测旋转轴坐标系x轴方向平行,即球杆仪测量的是旋转轴坐标系x方向的综合线性误差；位置2和6处球杆仪的方向与被测旋转轴坐标系y轴方向平行,测量旋转轴坐标系y方向的综合线性差；位置3处球杆仪位于测旋转轴坐标系Z轴,量旋转轴坐标系z方向的综合线性误差.那么由（8）可以得到六圈法中各个位置处的综合误差为

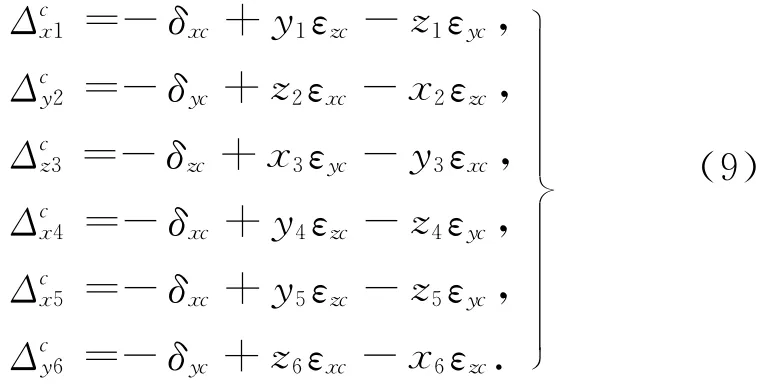
则矩阵形式可表示为

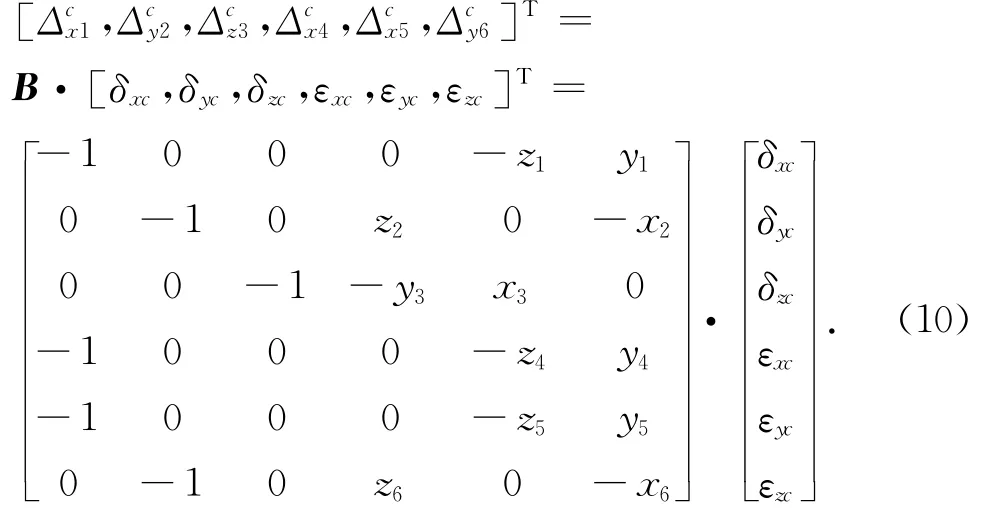
为了能够辨识得到几何误差项,就需要选择合适的坐标值来保证矩阵B满秩.同时为了辨识方便,六圈法中6个位置应尽可能在坐标轴上,如图3所示,即位置1,2,3分别位于旋转轴x,y,z轴上,则式（10）中辨识矩阵变为

式中：z1≠z5,y4≠0.理想状态是z1为0,而z5不为0,但是由于机床结构以及工作台的安装等很难保证z1为0,故只需保证z1≠z5即可.则C轴6项几何误差表示为

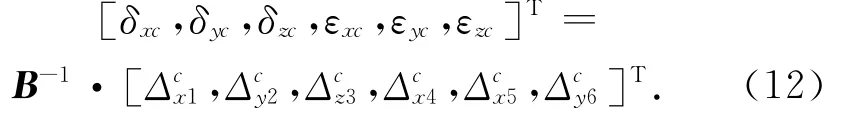
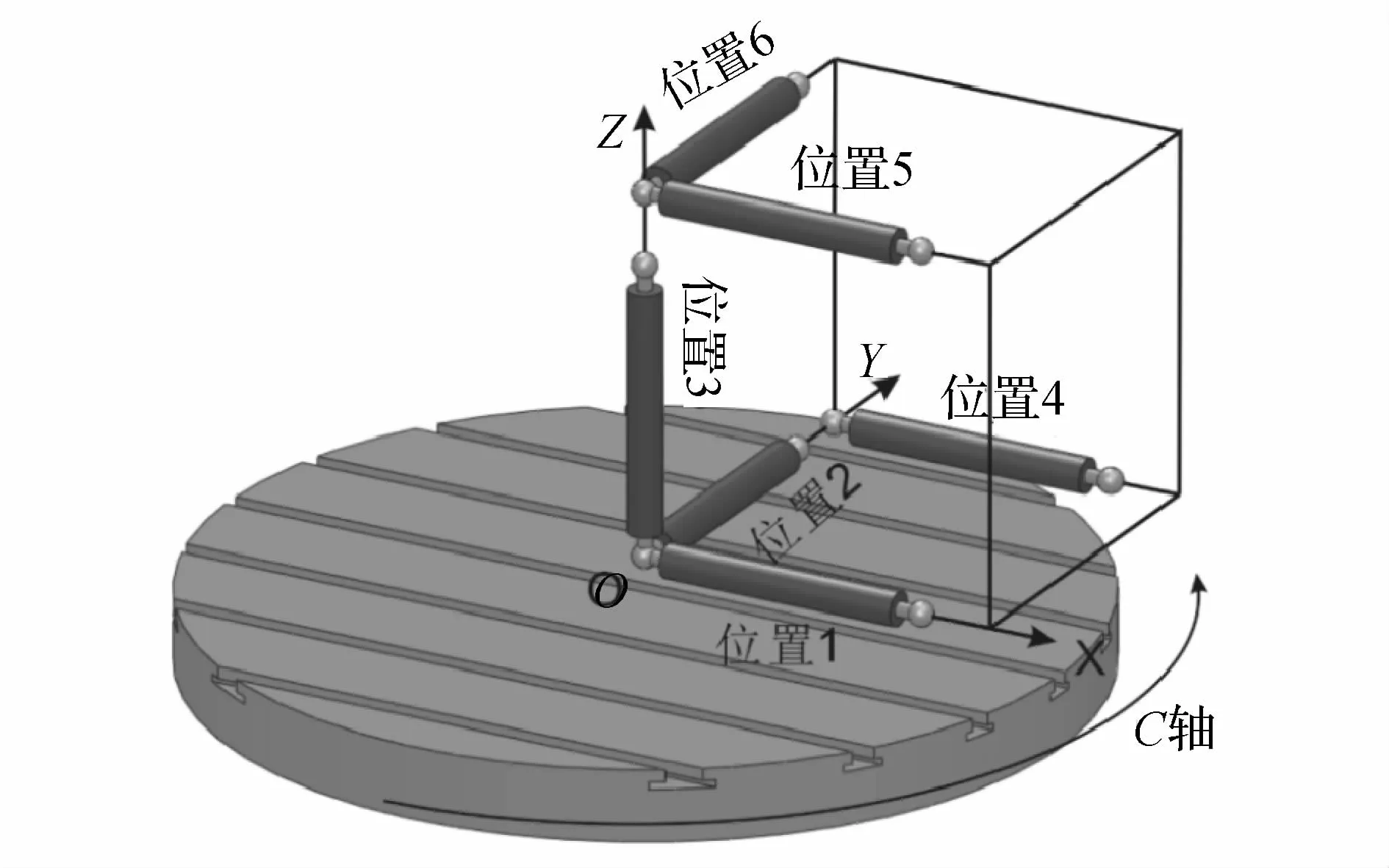
图3 六圈法中球杆仪6个位置示意图Fig.3 Six positions of ballbar in six-circle technology

同理,对于A轴,六圈法中6个位置可与辨识C轴时相同,只是要求球杆仪与A轴同步旋转,且相应的读数记为A轴综合误差读数,这里同样先将垂直度误差作为相应转角误差的一部分,位置误差作为相应线性误差的一部分,则A轴6项几何误差为

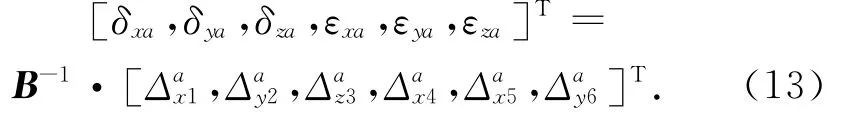
因为旋转轴旋转角度不同球杆仪读数就不同,则式（12）和（13）得到的基本误差项都是相对于旋转轴转角变化的值.

2.2 垂直度误差和位置误差辨识

六圈法中式（12）和式（13）是不考虑垂直度误差和位置误差,采取的处理方法是将垂直度误差作为转角误差的一部分,将位置误差作为线性误差的一部分.那么需要进一步辨识得到旋转轴的垂直度误差和位置误差.垂直度误差和位置误差是与旋转轴旋转角度无关的误差,表示相邻轴的角度和位置偏差关系,其误差值是一个恒定数值.而基本几何误差项是随着旋转轴旋转角度而变化的,而且在旋转轴零位置处的6项基本误差项定义为0.那么可以利用旋转轴初始位置处误差数值来辨识得到垂直度误差和位置误差.

用六圈法辨识C轴时将垂直度误差Scx作为转角误差εyc的一部分,而Scy是转角误差εxc的一部分,位置误差ocx作为线性误差δxc的一部分,ocy是线性误差δyc的一部分.因为在C轴转角为零时,转角误差εyc和εxc为0,同时线性误差δxc和δyc为0.所以在零角度处由式（12）辨识得到的转角误差εyc即为垂直度误差Scx,转角误差εxc即为垂直度误差Scy,线性误差δxc即为位置误差ocx,线性误差δyc即为安装误差ocy,那么

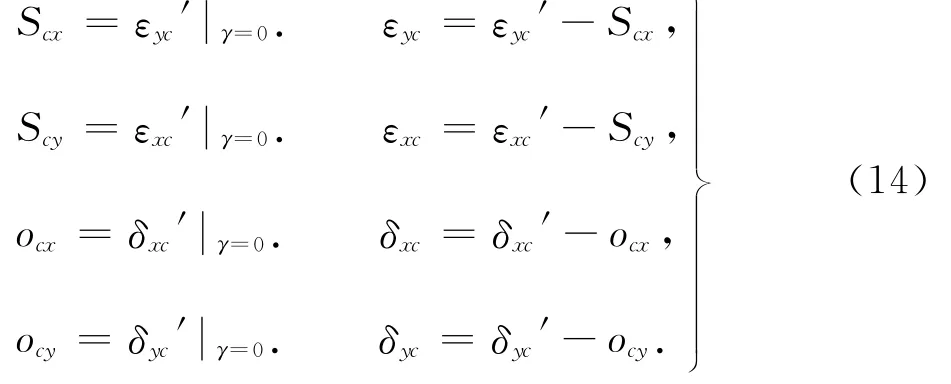
式中：εyc′和εxc′表示由式（12）辨识得到相应的转角误差,δxc′和δyc′表示由式（12）辨识得到的相应的线性误差.

辨识A轴时是将垂直度误差Say作为转角误差εza的一部分,而Saz是转角误差εya的一部分,位置误差oay作为线性误差δya的一部分,oaz是线性误差δza的一部分那么用同样的方法可以得到这垂直度误差和位置：

式中：εza′和εya′表示由式（13）辨识得到的相应的转角误差,δya′和δza′表示由式（13）辨识得到的相应的线性误差.

这样基于球杆仪的六圈法辨识得到了每个旋转轴的10项几何误差.为了进一步提高辨识精度,六圈法中每个位置处进行多次测量得到多组球杆仪读数.同时因为六圈法中位置1,2和3这3处的工件球位置是一样的,位置5和6处的工件球位置是一样的,则该方法只需安装调整3次球杆仪中与工件球相连的中心座的位置.同时因为在初始位置时2个旋转轴的坐标系是重合的,则在测量A轴和C轴时这6个位置是相同的,那么每个位置处只需装夹球杆仪一次即可测量A轴和C轴,即采集完C轴辨识数据后,接着采集A轴相应的辨识数据,只需运行相应的NC代码即可,这样整个过程中就可以大大的减少球杆仪的装夹次数,在很大程度上提高了六圈法的测量效率,达到快速测量的目的.另外,与平动轴的9线法类似,六圈法适合于不同的旋转轴测量,也没有机床几何模型原理误差.

3 球杆仪安装误差处理方法

3.1 安装误差的的影响与辨识

球杆仪测量时需要对球杆仪进行安装,很难保证工件球和刀具球能够安装在理想位置,这就不可避免的会产生安装误差.安装误差在一定程度上对辨识精度产生影响,那就需要从测量数据中消除安装误差的影响来保证辨识精度.

一种方法是在测量辨识旋转轴后单独运行与旋转轴同步运动的平动轴来辨识球杆仪的安装误差［10］.另一种方法是设计一种微调装置,来调节球杆仪2个球的安装位置［13］.但是这2种方法对于“六圈法”来说就比较繁琐,且会大大增加测量工作量,甚至需要额外制造精密的微调装置.对于六圈法,最好的方法是通过分析球杆仪安装误差对辨识精度的影响并对测量数据进行分析处理来消除安装误差.

球杆仪刀具球和工件球都存在安装误差,这样就使得工件球的坐标和刀具球的坐标与理想坐标产生偏差.假设刀具球在x,y,z这3个方向上的安装误差分别为tx,ty和tz,工件球的安装误差分别为wx, wy和wz.那么机床综合几何误差模型应表示为

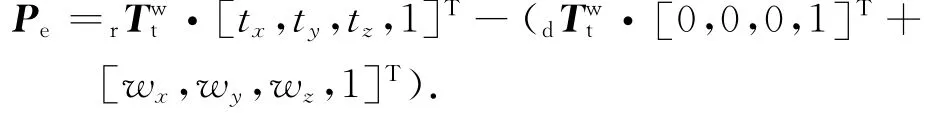
那么测量C轴时综合误差应表示为

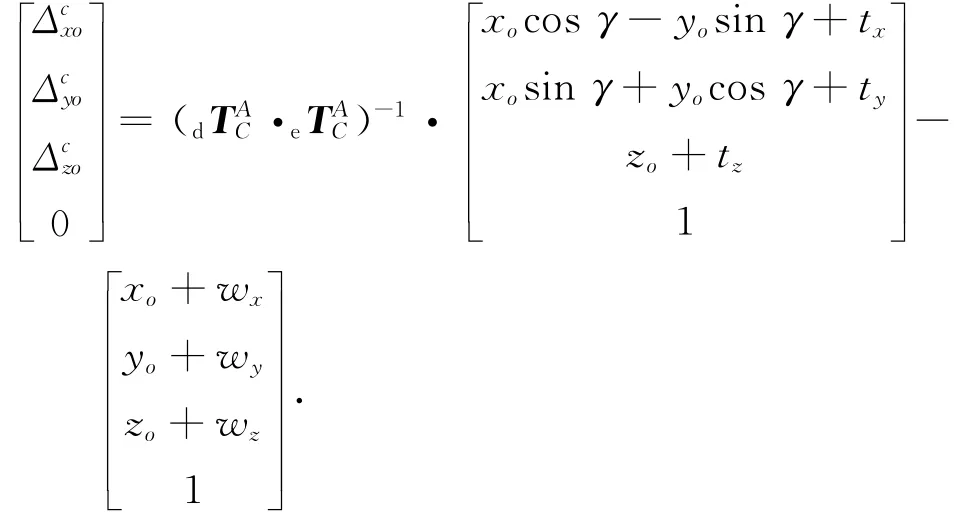
整理后得到包含安装误差在内的球杆仪的误差读数为

同样的,对于A轴,球杆仪的误差读数为

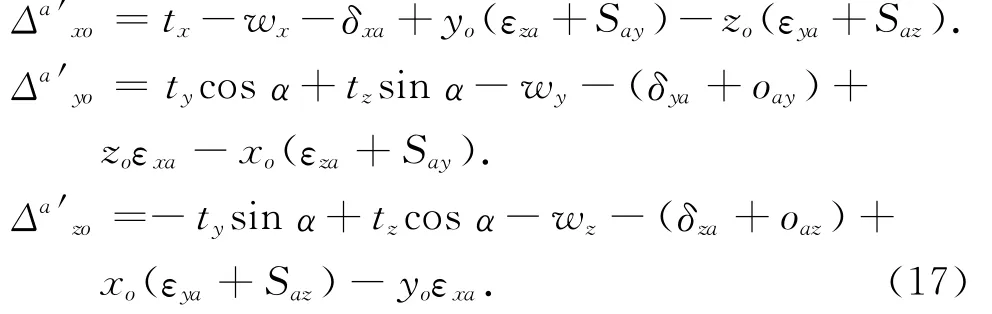
式中：Δa′xo、Δa′yo、Δa′zo、分别表示A轴运动时在x、y、z方向上包含安装误差在内的球杆仪误差读数.可以看到不同的安装误差对同一方向球杆仪读数的影响是不同的,同时同一个误差对不同方向上读数影响也不同,所以安装误差对“六圈法”中不同位置处的影响是不同的.这些球杆仪读数对不同位置处的影响可以通过仿真分析来得到［7］.

同时式（17）也直接表明工件球的安装误差影响球杆仪轨迹的半径,而刀具球的安装误差的影响比较复杂,它们会给C轴x方向和y方向上的球杆仪轨迹带来偏心误差,给z方向造成半径偏差,而对A轴测量则会造成y方向和z方向上的球杆仪轨迹偏心,带来x方向的半径误差.球杆仪读数与球杆仪公称长度之间的差值即为测量的该方向的综合误差,而球杆仪可以辨识的误差范围为±1 mm,其远远小于球杆仪公称长度,所以球杆仪读数本身还是保持一个圆的形状,即球杆仪轨迹本身还是一个近似圆,并没有发生很大的畸形变化.那么安装误差对于六圈法中各个位置球杆仪轨迹的影响可以详细的分析得到,见表1.

可以根据球杆仪读数利用最小二乘法得到安装误差.数控机床各个几何误差项是在微米级别的,而球杆仪的安装误差很难保证在微米级别,甚至于0.1 mm级别的,那么就说明安装误差相对于机床的几何误差项数量级大,所以最佳拟合圆的半径偏差和偏心可以认为是安装误差造成的.根据式（16）和（17）只考虑安装误差影响,对各个位置处球杆仪读数采用最小二乘法得到相应的安装误差.那么就可以从测量数据中直接剔除安装误差,在式（16）和（17）基础上可以式（18）和式（19）,从测量数据中减去安装误差对各个方向（位置上）的影响,得到只包含机床几何误差项的综合误差读数,然后根据六圈法辨识公式得到旋转轴相应的几何误差.

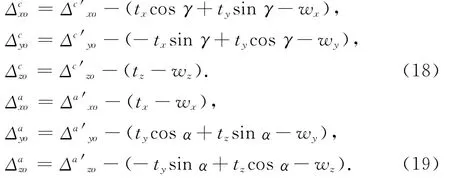
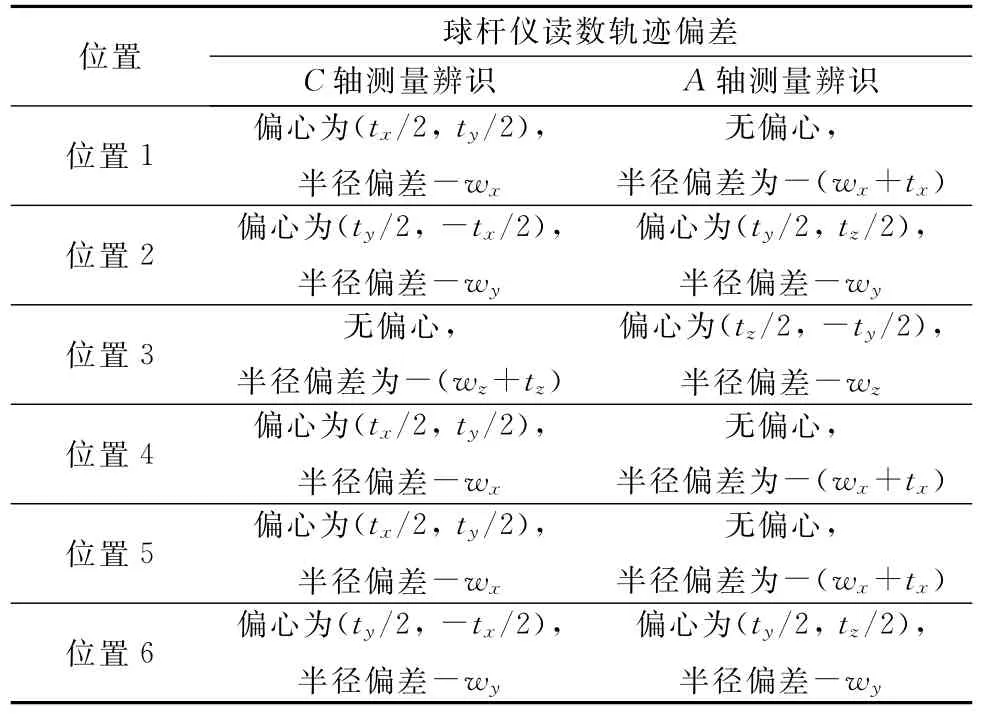
表1 安装误差对六圈法中球杆仪轨迹的影响Tab.1 Influences of set-up errors on trajectory of ballbar in six-circle technology

3.2 安装误差的仿真

以测量C轴为例来对六圈法中球杆仪安装误差进行仿真验证.首先产生C轴的几何误差项数据和球杆仪安装误差,其中6项基本几何误差项随机产生,其随C轴旋转角度的变化而变化,垂直度误差,位置误差以及安装误差为定值,如表2所示为仿真产生的球杆仪安装误差数据.然后根据机床几何误差模型计算六圈法中各个位置读数,其中数据额外增加噪声的影响,如图4所示为仿真得到球杆仪读数数据,设球杆仪公称长度为100 mm.接着对球杆仪读数进行最小二乘法拟合,得到球杆仪安装误差.如表3所示为各个位置处安装误差的仿真结果.计算得到的安装误差与仿真产生的安装误差的最大残差为－6.8和6.3μm,仿真结果表明辨识球杆仪安装误差的可行性与正确性.那么就可以从球杆仪测量数据中剔除安装误差来提高六圈法的精度.

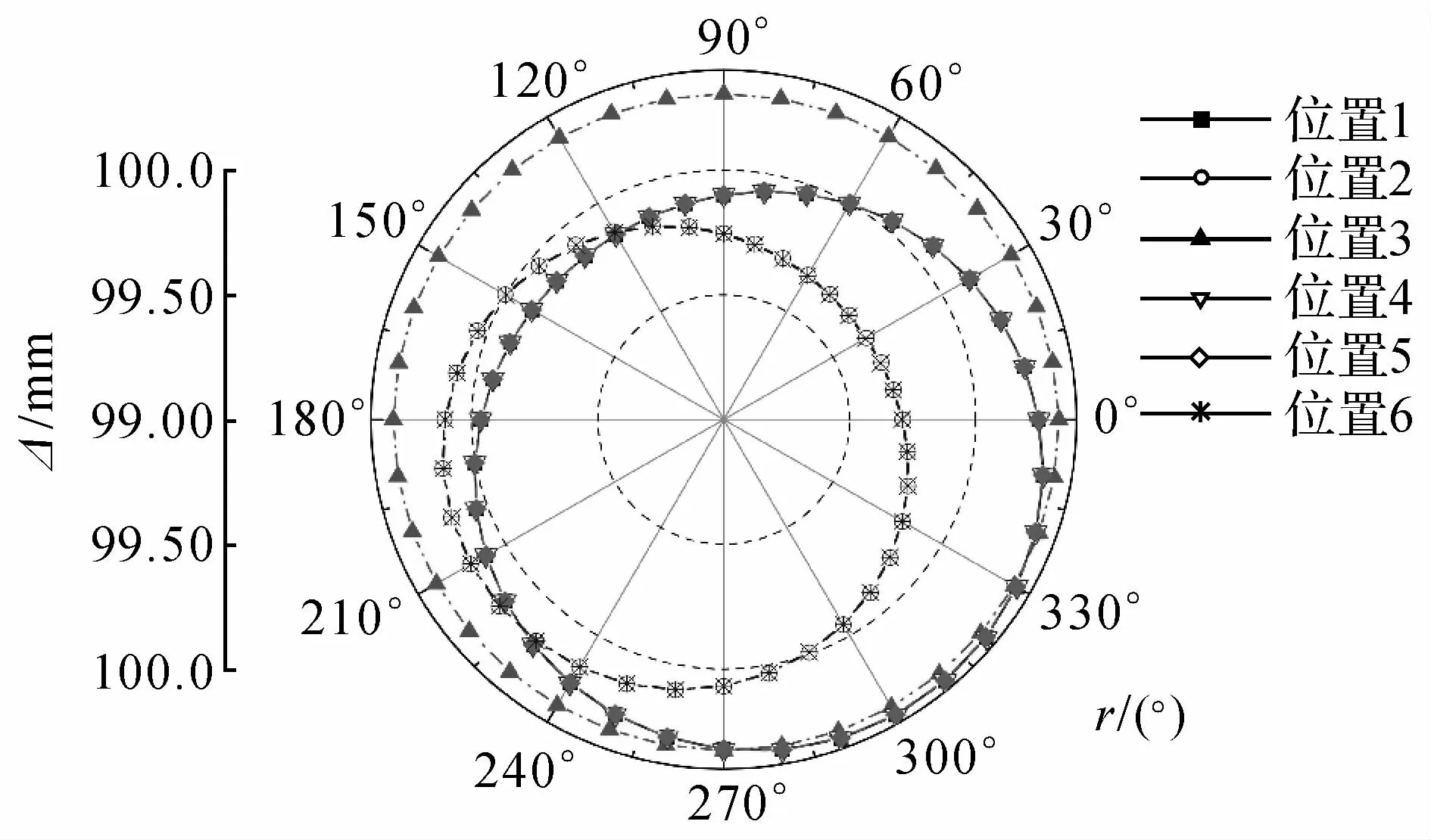
图4 六圈法测量时各个位置处球杆仪仿真读数Fig.4 Simulated ballbar readings of each position with six-circle technology

表2 仿真产生的刀具球和工件球安装误差Tab.2 Generated set-up errors for simulationμm

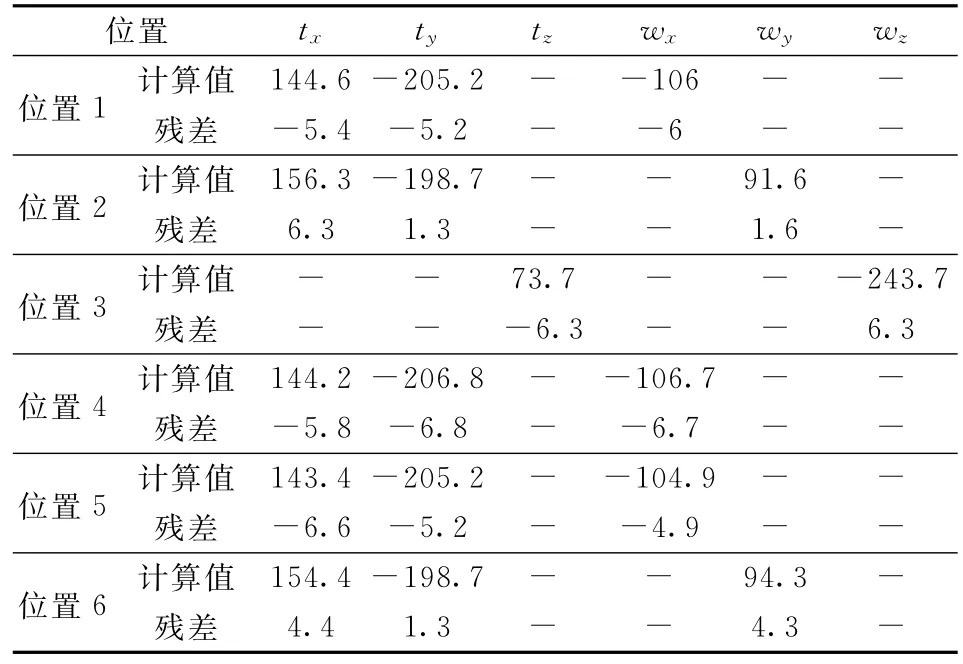
表3 计算得到的各个位置的安装误差以及相应残差Tab.3 Calculated set-up errors and corresponding residual error for each position μm

4 实验验证

用雷尼绍公司的QW20球杆仪采用本文的六圈法对北京精雕Smart CNC500五轴加工中心进行旋转轴几何误差辨识,如图5所示.因为机床结构限制,六圈法中位置1、2、3的z坐标不能够为0,根据安装实际情况使得z1＝68 mm,位置4的y4＝40 mm,位置5和6的z5＝90 mm,那么就可以得到辨识矩阵B.C轴的旋转角度为0到360°,A轴为－90°～90°.每个位置处C轴测量数据采集完后,然后进行A轴的测量,完成后再进行下个位置的测量数据采集.如图6所示为六圈法辨识C轴时各个位置处的测量数据,如图7所示为辨识A轴的各个位置处测量数据.对于A轴,0～90°和0～－90°是分开测量的.由于机床Z轴行程的限制,使得位置2处和5处球杆仪无法从－90°直接旋转至90°,采取的方法是－90°到0°和0到90°分开测量,这2个阶段球杆仪方向相反,以保证Z轴在行程范围内.同时图7表明球杆仪读数0到90°和0到－90°是在2个不同的圆上,这就是由于测量时不是一次性测量造成的.也可以通过改变位置2和5处y坐标来保证同步运动时Z轴在行程范围内从而避免这种问题.对各组数据进行最小二乘法拟合,得到各个位置处的安装误差.消除安装误差的影响后,利用六圈法辨识原理得到旋转轴的各项几何误差.如图8（a）所示为辨识得到的C轴线性误差曲线图,图8（b）为C轴转角误差曲线图；如图9（a）所示为A轴线性误差曲线图,图9（b）为A轴转角误差曲线图.如表4所示为辨识得到的2个旋转轴的垂直度误差和位置误差.

图5 球杆仪六圈法测量旋转轴误差Fig.5 Scenes of measurement for rotary axis using sixcircle technology with ballbar

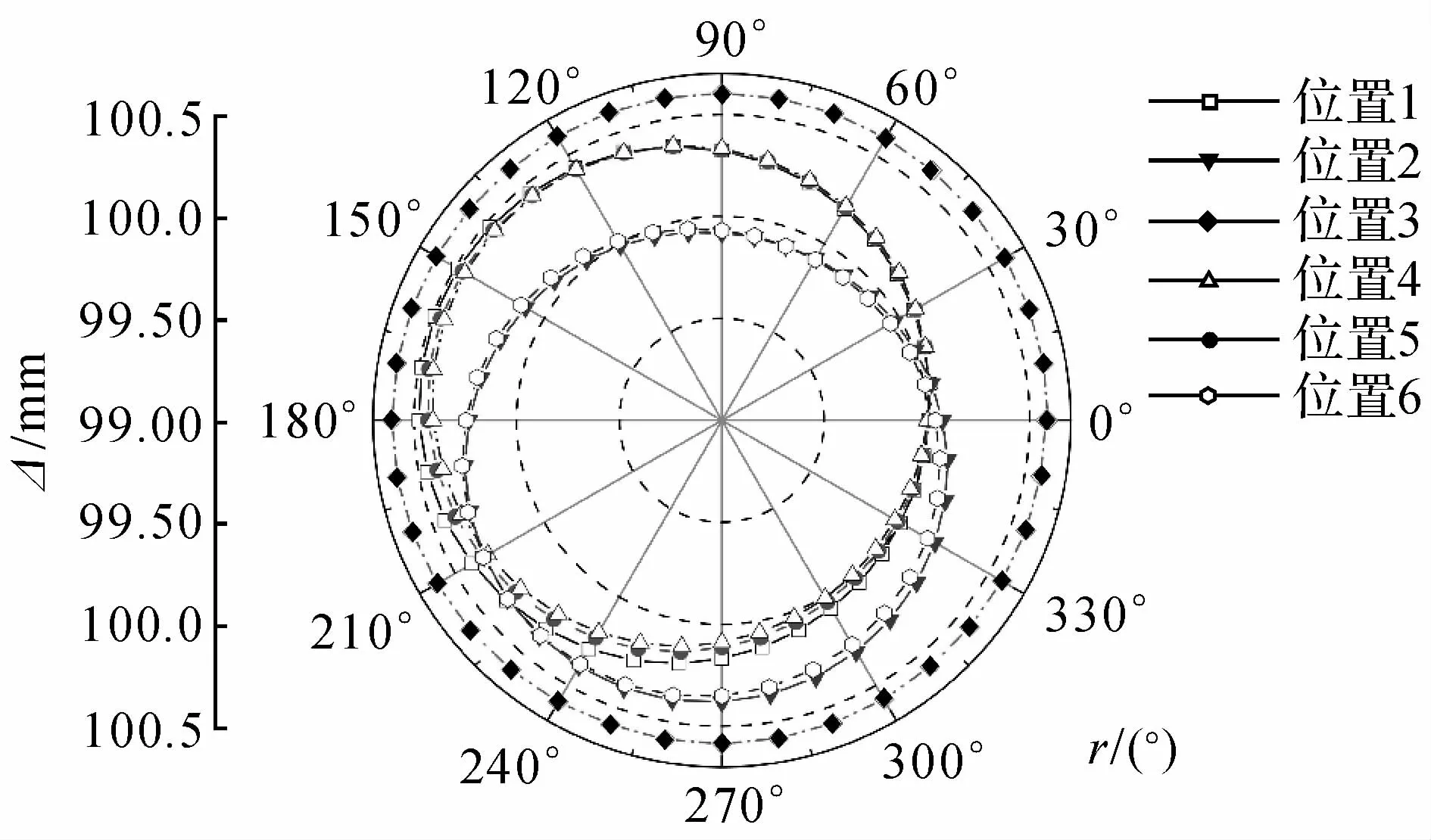
图6 六圈法测量C轴时各个位置处球杆仪读数Fig.6 Ballbar readings of each position for C-axis identification with six-circle technology

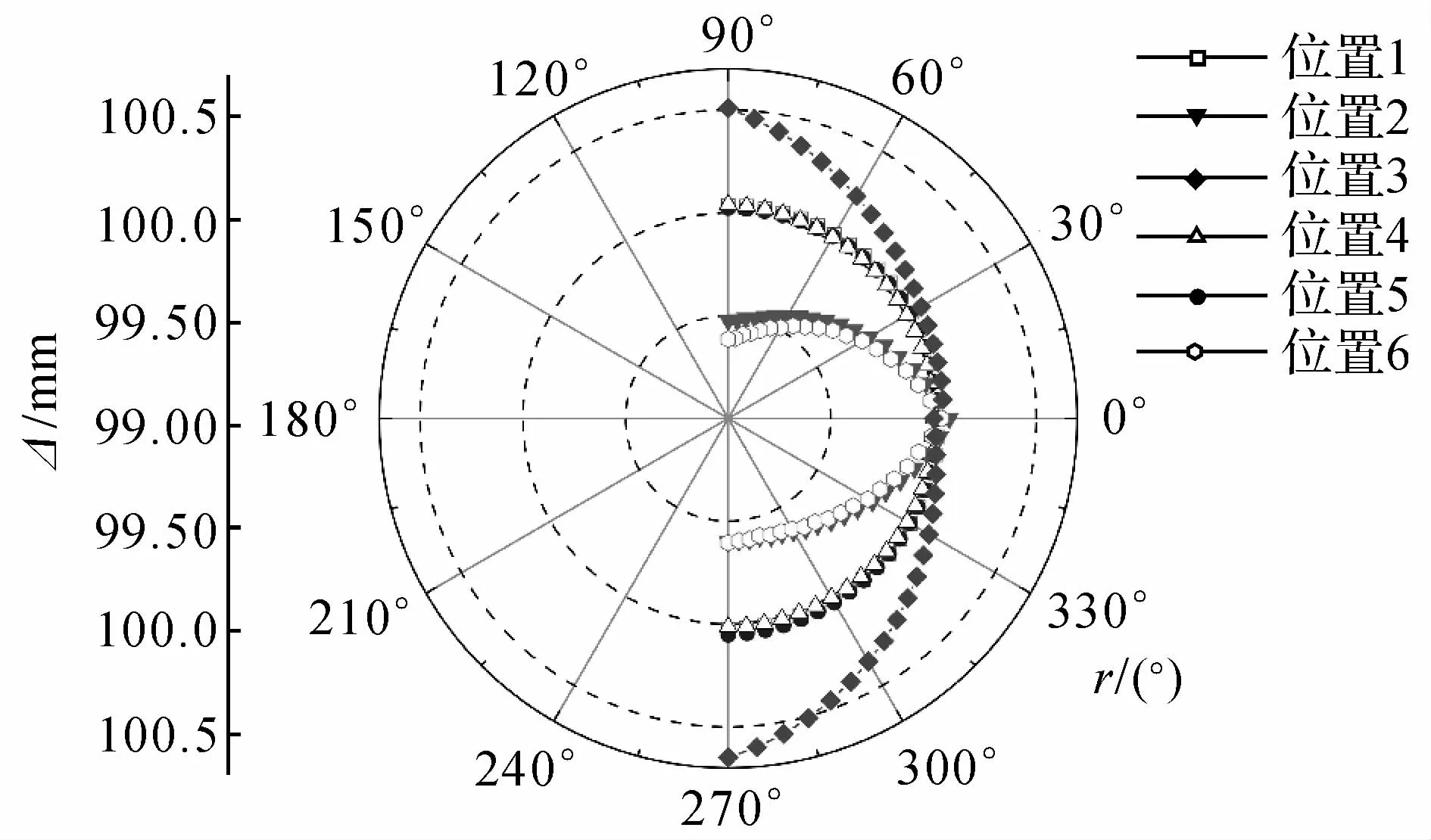
图7 六圈法测量A轴时各个位置处球杆仪读数Fig.7 Ballbar readings of each position for A-axis identification with six-circle technology

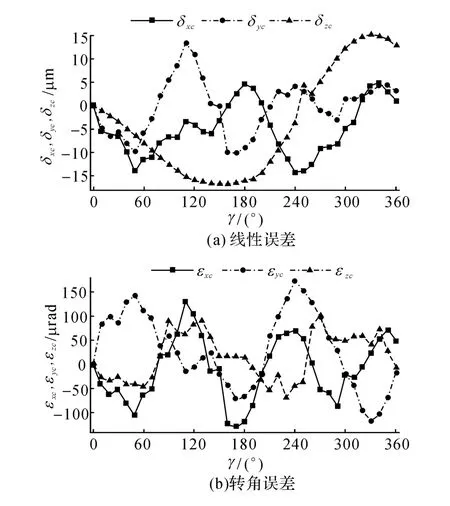
图8 辨识得到的C轴6项基本误差项Fig.8 Six identified basic geometric errors of C-axis

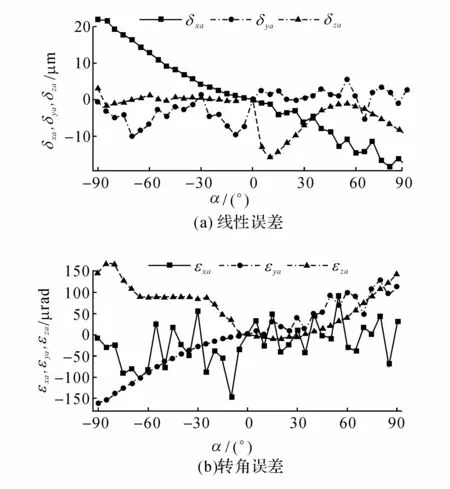
图9 辨识得到的A轴6项基本误差Fig.9 Six identified basic geometric errors of A-axis

表4 2个旋转轴的垂直度误差和位置误差Tab.4 Squareness errors and offset errors of two rotary axes

为了进一步验证六圈法的辨识精度,可将辨识得到的旋转轴误差进行补偿,然后测量补偿后各个位置处球杆仪读数,并与未补偿的测量读数进行比较.辨识得到的旋转轴误差值,可用相应的平动轴来补偿,如C轴δxc和εyc影响机床位置1精度,可将C轴误差值通过X和Y轴来补偿；对位置2,C轴δyc和εxc的影响也可通过X和Y轴来补偿.如图10所示为位置1处C轴δxc和εyc误差补偿前后球杆仪测量值的比较图,如图11所示为位置2处C轴δyc和εxc误差补偿前后球杆仪测量值的比较图.第3组数据是消除安装误差和C轴误差后的计算值.

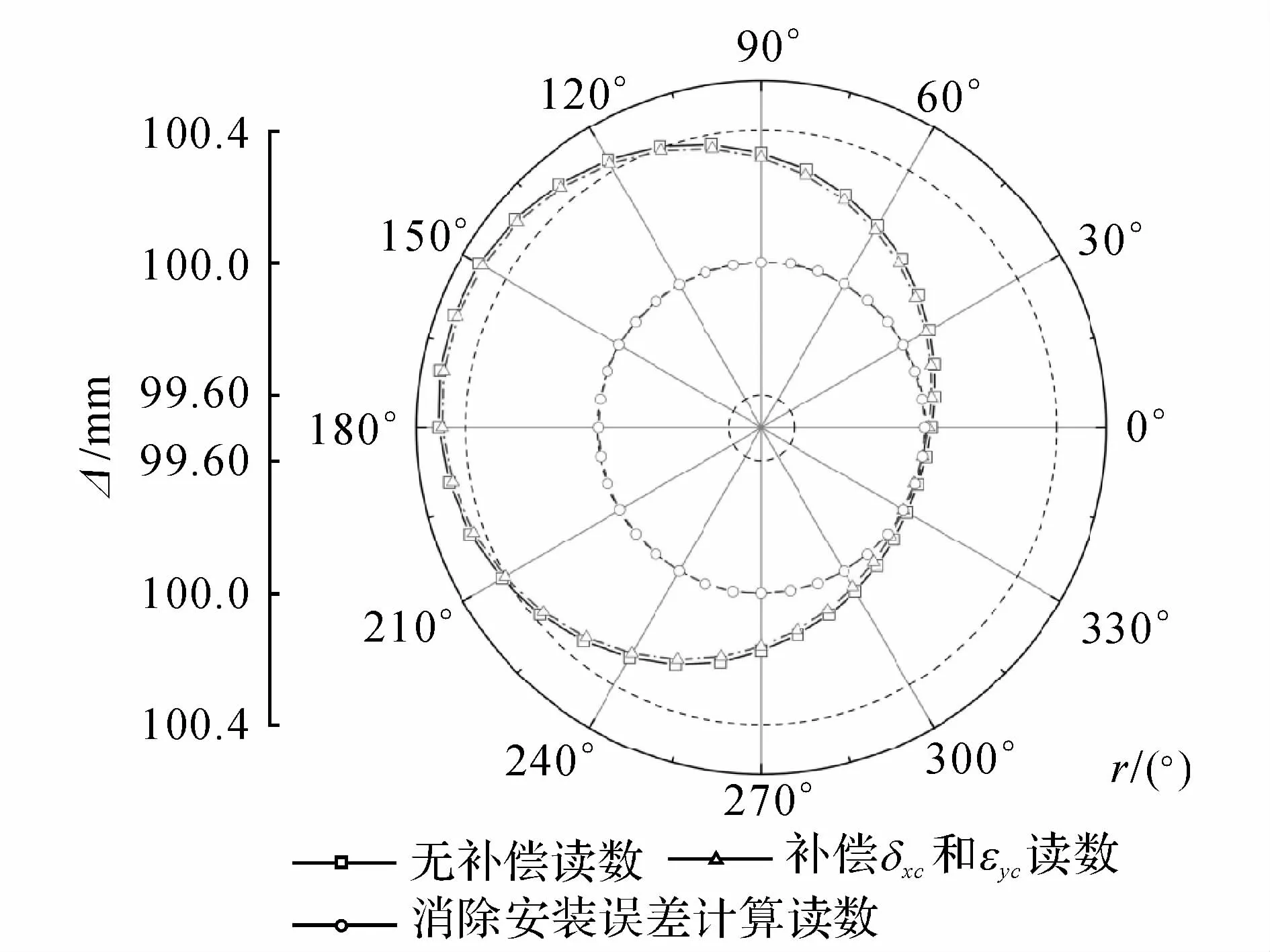
图10 位置1处δxc和εyc误差补偿前后测量数据Fig.10 Measured data of first position one with and without compensation ofδxc andεyc

为了更清楚地比较误差补偿效果,对补偿前后的球杆仪读数采用安装误差分类方法进行消除安装误差处理.如图12所示为位置1处补偿前后读数消除安装误差后的数据比较图,如图13所示为位置2处补偿前后读数消除安装误差后的数据比较图.其中第3组数据为理想的标准圆轨迹读数.消除安装误差后,位置1处误差从±5μm减少到±0.9μm内,补偿后的误差减少了80%,而且补偿后轨迹圆度大大提高.位置2处补偿前误差从－2.86μm到4.47μm,补偿后误差减少到±2μm内,降低了50%左右,补偿效果明显,同时补偿后球杆仪轨迹圆度也有明显提高.那么进一步验证了六圈法误差辨识精度高.

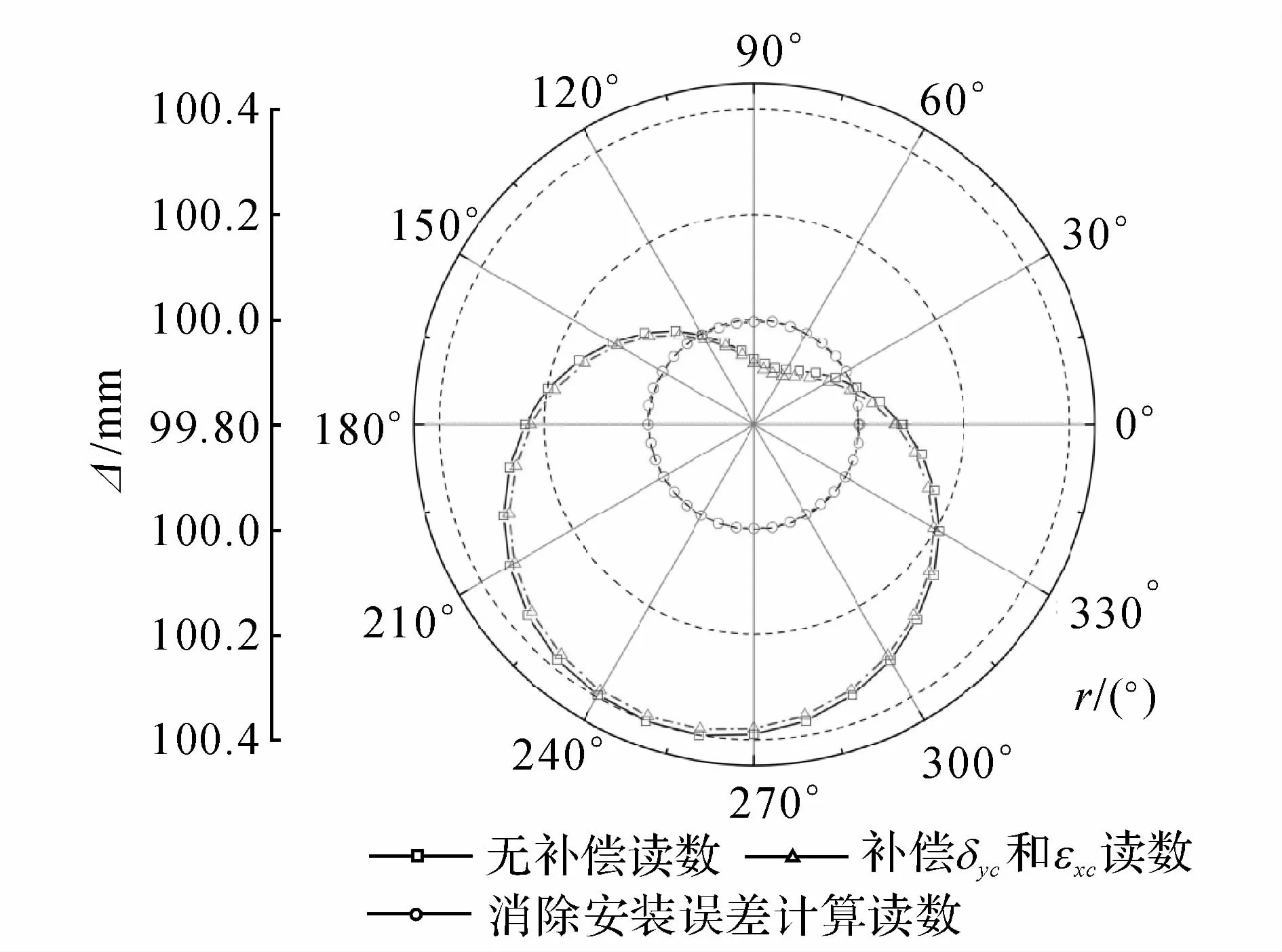
图11 位置2处δyc和εxc误差补偿前后测量数据Fig.11 Measured data of second position with and without compensation ofδyc andεxc

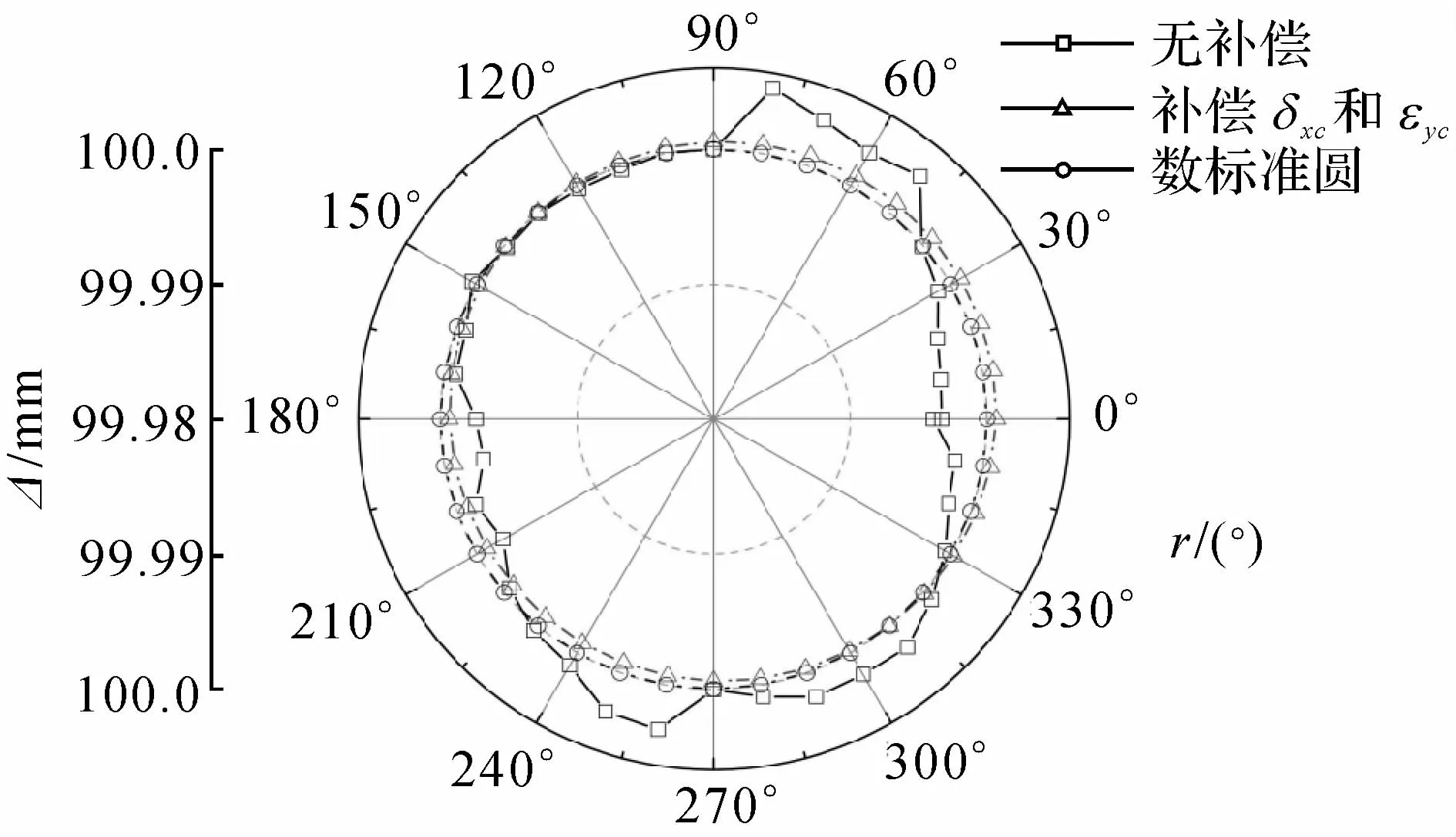
图12 位置1处消除安装误差后对比数据Fig.12 Data of first position without set-up errors

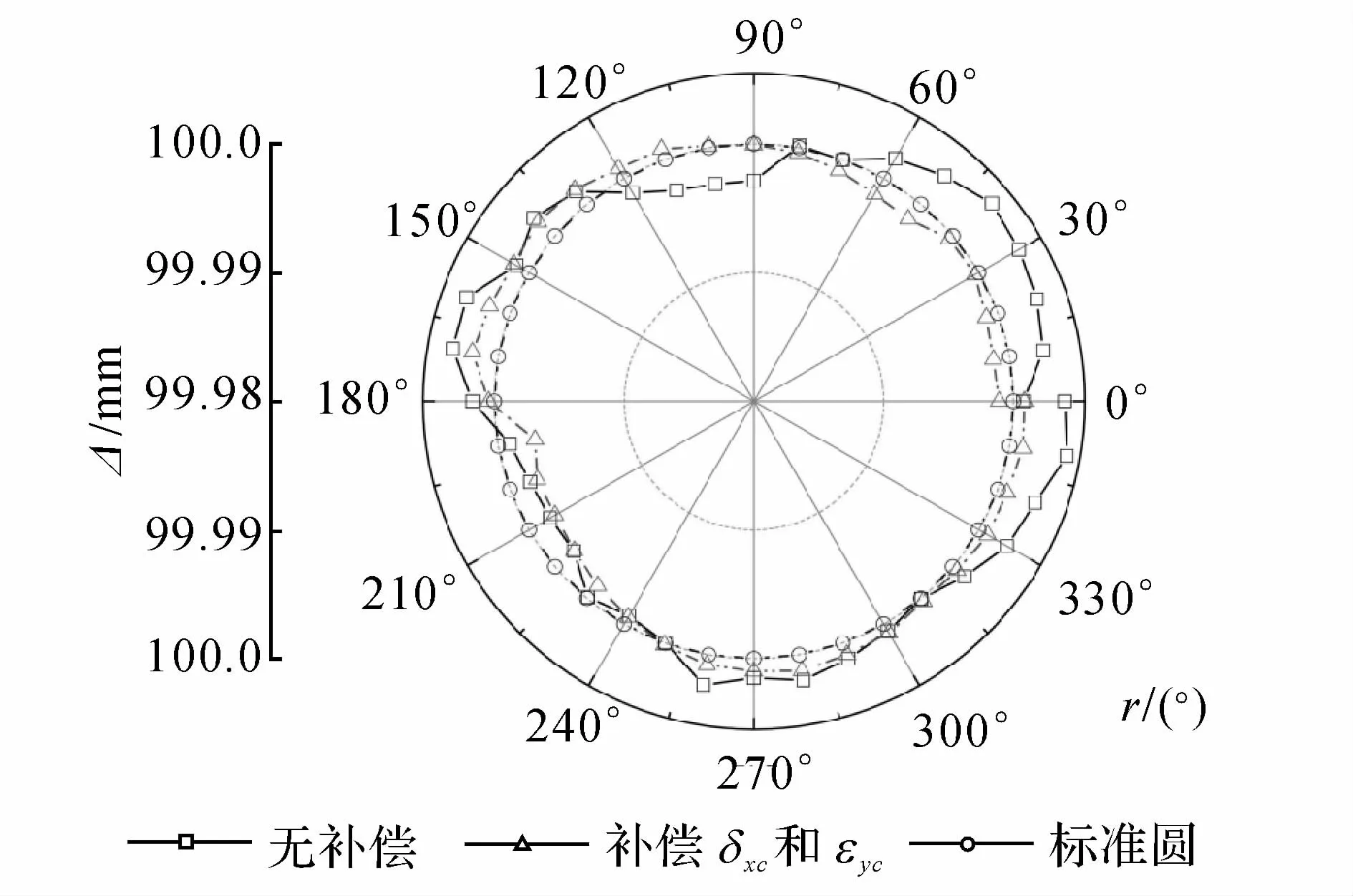
图13 位置2处消除安装误差后对比数据Fig.13 Data of the second position without set-up errors

5 结 论

旋转轴几何误差辨识是五轴数控机床几何误差建模与补偿的基础,本文提出了基于球杆仪测量的六圈法来系统地、快速地辨识双转台五轴机床2个旋转轴的全部几何误差项.

（1）从机床几何模型出发分析得到旋转轴误差辨识原理与平动轴9线法相同,提出了基于球杆仪的六圈法来辨识旋转轴基本几何误差项,然后通过分析几何误差项的性质辨识得到旋转轴的垂直度误差和位置误差.该方法中球杆仪安装次数少,测量方便、快速,可系统地得到每个旋转轴10项几何误差.同时可辨识不同的旋转轴,且无原理误差.

（2）具体分析球杆仪工件球和刀具球安装误差在每个位置处对球杆仪轨迹的影响,然后采用最小二乘法对球杆仪读数拟合得到相应的安装误差,从而消除其对六圈法辨识精度的影响,并仿真验证该方法得到安装误差的正确性与可行性.

（3）以精雕SmartCNC500为例,采用本文的六圈法测量辨识A轴和C轴的几何误差,测量方便快捷.同时比较旋转轴误差补偿前后的测量值来验证六圈法的可行性与准确性.

（References）：

［1］SHEN H,FU J,HE Y,et al.On-line asynchronous compensation methods for static／quasi-static error implemented on CNC machine tools［J］.International Journal of Machine Tools and Manufacture,2012.60（0）：14-26.

［2］王金栋,郭俊杰,费致根,等.基于激光跟踪仪的数控机床几何误差辨识方法［J］.机械工程学报,2011（14）：13-19.

WANG Jin-dong,GUO Jun-jie,FEI Zhi-gen,et al.Method of geometric error identification for numerical control machine tool based on laser tracker［J］.Chinese Journal of Mechanical Engineering,2011.47（14）：13-19.

［3］ZHU S,DING G,QIN S,et al.Integrated geometric error modeling,identification and compensation of CNC machine tools［J］.International Journal of Machine Tools and Manufacture,2012.52（1）：24-29.

［4］FU G,FU J,XU Y,et al.Product of exponential model for geometric error integration of multi-axis machine tools［J］.The International Journal of Advanced Manufacturing Technology,2014.71（9／12）：1653-1667.

［5］LEI W T,HSU Y Y.Error measurement of five-axis CNC machines with 3D probe-ball［J］.Journal of Materials Processing Technology,2003.139（1／3）：127-133.

［6］WEIKERT S.R-Test,A new device for accuracy measurements on five axis machine tools［J］.CIRP Annals-Manufacturing Technology,2004.53（1）：429-432.

［7］ZARGARBASHI S H H,MAYER J R R,Assessment of machine tool trunnion axis motion error,using magnetic double ball bar［J］.International Journal of Machine Tools and Manufacture,2006.46（14）：1823-1834.

［8］TSUTSUMI M,SAITO A.Identification and compensation of systematic deviations particular to 5-axis machining centers［J］.International Journal of Machine Tools and Manufacture,2003.43（8）：771-780.

［9］TSUTSUMI M,SAITO A.Identification of angular and positional deviations inherent to 5-axis machining centers with a tilting-rotary table by simultaneous four-axis control movements［J］.International Journal of Machine Tools and Manufacture,2004.44（12／13）：1333-1342.

［10］TSUTSUMI M,TONE S,KATO N,et al.Enhancement of geometric accuracy of five-axis machining centers based on identification and compensation of geometric deviations［J］.International Journal of Machine Tools&Manufacture,2013,68：11-20.

［11］LEE K I,LEE D M,YANG S H.Parametric modeling and estimation of geometric errors for a rotary axis using double ball-bar［J］.International Journal of Advanced Manufacturing Technology,2012.62（5／8）：741-750.

［12］LEE K I,YANG S H.Robust measurement method and uncertainty analysis for position-independent geometric errors of a rotary axis using a double ball-bar［J］.International Journal of Precision Engineering and Manufacturing,2013.14（2）：231-239.

［13］LEE K I,YANG S H.Measurement and verification of position-independent geometric errors of a five-axis machine tool using a double ball-bar［J］.International Journal of Machine Tools and Manufacture,2013.70（0）：45-52.

［14］胡建忠,王波雷,王民,等.基于双频激光干涉仪的DM1007数控铣床几何误差辨识的实验研究［J］.制造技术与机床,2010（04）：103-106.

HU Jian-zhong,WANG Bo-lei,WANG Min,et al.The study of geometric error identification of DM1007 milling machine based on laser interferometer［J］.Manufacturing Technology&Machine Tool,2010（4）：103-106.

［15］HE Z Y,FU J Z,YAO X H.Volumetric error modeling and Analysis for CNC machine tool based on multibody system［J］.Key Engineering Materials,2010.426-427：441-446.

［16］LIN Y,SHEN Y.Modelling of five-axis machine tool metrology models using the matrix summation approach［J］.The International Journal of Advanced Manufacturing Technology,2003.21（4）：243-248.

One novel geometric error identification of rotary axes for five-axis machine tool

FU Guo-qiang,FU Jian-zhong,SHEN Hong-yao
（The State Key Laboratory of Fluid Power Transmission and Control,Zhejiang University,Hangzhou 310027,China）

In order to obtain all the geometric errors of rotary axes for a five-axis machine tool systematically and easily,a geometric error identification approach with ballbar measurement,six-circle technology,is developed.The influences of geometric errors of rotary axes on the integrated errors of five-axis CNC machine tools were obtained based on the geometric error model.By comparing with the nine-line method of linear axes,six-circle technology was established due to the characteristic of ballbar.This approach identified all the ten errors of each axis,including squareness errors and offset errors through analyzing the property of geometric errors.The impact of the set-up errors of ballbar was analyzed to improve the accuracy of six-circle technology.The set-up errors were obtained using the least square method,and they were removed from the measured data of ballbar.He simulation validated that elimination of set-up errors is appropriate enough.Six-circle technology was used to identify the geometric errors of rotary axes for five-axis machine tools.The measured data with compensation of geometric errors of rotary axis were compared with those without compensation.The measured errors with compensation decreased about from 50%to 80%.The experiments show that six-circle technology is precise in a systematic way and can identify different types of rotary axes.

six-circle technology；ballbar；rotary axis；geometric error；set-up error

傅建中,男,教授,博导.E-mail：fjz＠zju.edu.cn

TH 161

A

1008-973X（2015）05-0848-10

10.3785／j.issn.1008-973X.2015.05.006

2014-05-26. 浙江大学学报（工学版）网址：www.journals.zju.edu.cn／eng

国家自然科学基金资助项目（51175461）；高等学校博士学科点专项科研基金资助项目（20120101110055）浙江省自然科学基金项目（Y14E050069）.

付国强（1988－）,男,博士生,从事精密仪器、先进数控技术研究工作.E-mail：fuguoqiang_1988＠126.com