综合模态控制力下压电致动器的优化布局

杨依领,娄军强,魏燕定,傅 雷,田 埂,赵晓伟

（1.浙江大学现代制造工程研究所浙江省先进制造技术重点研究实验室,浙江杭州310027；2.宁波大学机械与力学学院,浙江宁波315211）

综合模态控制力下压电致动器的优化布局

杨依领1,娄军强2,魏燕定1,傅 雷1,田 埂1,赵晓伟1

（1.浙江大学现代制造工程研究所浙江省先进制造技术重点研究实验室,浙江杭州310027；2.宁波大学机械与力学学院,浙江宁波315211）

针对智能挠性结构中致动器的优化布局问题,在分析挠性结构动力学方程和状态空间方程的基础上,采用模态理论,对系统控制矩阵进行奇异值分解,提出一种表征最大综合模态控制力的评价准则,该评价准则兼顾保留模态和截断模态对模态控制力的影响,综合考虑模态权重.最后以粘贴有压电致动器／应变传感器的挠性梁为例,通过理论计算和改进的遗传算法进行优化分析,得到综合模态控制力最大时压电致动器的布局位置,并建立实验测控系统进行验证.实验结果表明：采用优化结果中的致动器布局时,系统具有较好的综合模态控制力,控制效果也更优,所提出的评价准则和优化方法是可行的.

智能挠性结构；综合模态控制力；压电致动器；优化布局

由于具有质量轻、操作空间大、发射成本低和能耗低等优点,挠性结构被广泛地应用在航空航天领域［1-2］.然而,在使用过程中,挠性结构因自身低刚度、低阻尼和低固有频率等特性,很容易产生弹性振动,影响系统的性能,因此需要对挠性结构进行振动控制研究［3］.

压电材料制成的致动器具有频响宽、响应速度快和动态性好等优点,被广泛地应用于智能挠性结构的主动振动控制［4-5］.致动器／传感器的布局位置密切影响着挠性结构的控制性能,不当的布局位置会导致系统产生控制和观测溢出等问题［6］,因此,有必要对智能挠性结构中致动器／传感器的优化布局进行研究.

对于挠性结构中致动器／传感器的优化布局问题,国内外许多研究者进行了相关研究.系统能控性／能观性准则广泛地应用在致动器／传感器的优化布局中,钱锋等［7］研究模态能控准则下致动器／传感器的优化布局问题.考虑致动器的致动能力,Lindberg等［8］研究了简单控制力准则下致动器的优化布局问题；考虑到模态截断会导致溢出效应,Ambrosio等［9］和邱志成［10］通过采用H2范数准则,研究了智能结构中致动器／传感器的布局问题；Bruant等［11］和Nestorovic等［12］在系统能控性／能观性的基础上,通过考虑截断模态来限制溢出效应,提出了一种改进的控制力准则,并对简支板上的压电致动器进行了优化布局研究.然而,对于智能挠性结构而言,振动具有多模态特性［13］,在实际应用中,传感器一般与致动器同位布局,而致动器的致动能力又往往有限,为了使控制效果达到最佳,又希望致动器对受控模态具有最大控制力［14］,因此需要对在综合模态下如何实现致动器的控制力最优这一问题,进行深入地研究.

针对智能挠性结构中致动器的优化布局问题,本文首先提出一种表征最大综合模态控制力的评价准则,然后以粘贴有压电致动器／应变传感器的挠性梁为例,通过理论计算和改进的遗传算法进行优化分析,得到综合模态控制力最大时压电致动器的布局位置,最后建立实验测控系统验证所述评价准则和优化方法的有效性.

1 系统建模

描述挠性结构振动的动力学方程一般可以表示为

式中：M为质量矩阵,K为刚度矩阵,F（t）为广义力矢量,x（t）为位移矢量.

考虑挠性结构的阻尼效应,得到挠性结构动力学方程的常微分方程形式：

式中：D为阻尼矩阵.

对式（2）作模态变换,得到挠性结构振动的模态坐标方程：

式中：q（t）为广义模态坐标矢量；Dm、Km和Bm分别为进行模态变换后的阻尼矩阵、刚度矩阵和控制矩阵；u（t）为输入矩阵.

为了对挠性结构进行特性分析,引入状态变量X（t）,得到挠性结构动力学方程的状态空间表达形式：

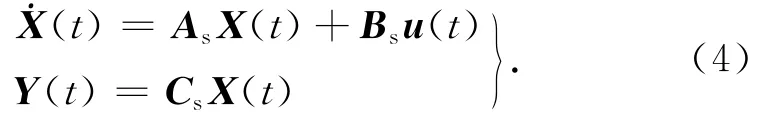
式中：X（t）为状态变量,是2k×1矩阵；Y（t）为输出变量,是p×1矩阵,具体表达式如下：

As,Bs,Cs分别为2k×2k状态矩阵、2k×r控制矩阵和p×2k输出矩阵,具体表达式如下：

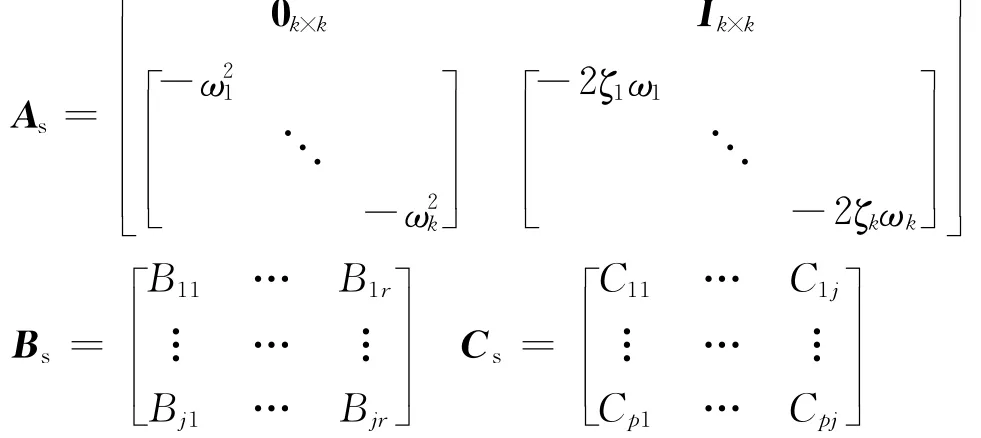
式中：ζk为第k阶模态阻尼比,ωk为第k阶固有频率,Bjr是与致动器位置有关的振型函数,Cpj是与传感器位置有关的振型函数,j等于2k.

2 评价准则

系统能控性用来分析输入变量u（t）对状态变量X（t）的控制能力,由系统状态方程中的状态矩阵As和控制矩阵Bs决定,而状态矩阵As取决于系统结构和内部参数,控制矩阵Bs则取决于控制力的施加位置.在智能挠性结构中,受致动器致动能力的制约,有必要对致动器的位置进行优化布局,希望致动器对受控模态具有最大控制力,以使控制效果达到最佳［14］.

根据式（4）,致动器控制力的表达式为

将式（5）两边分别左乘其转置矩阵,得到

采用奇异值分解,令Bs＝WSNT

式中：W为2k×2k矩阵,WTW＝I；N为r×r矩阵, NTN＝I；S为2k×r矩阵,其表达式如下：

代入式（6）,并进行简化可得

将v＝NTu代入式（7）,并进一步简化得到

式中：Δi代表矩阵S中第i行第i列的元素.

由于vTv＝uTu,从能量输入的角度来看,输入变量v与输入变量u等价.由式（8）可知,模态控制力与参数Δi和输入变量vi有关,参数Δi的大小取决于致动器的位置和大小；参数Δi越大,用于抑制挠性结构振动的输入变量越小；在同等输入情况下,致动器所能产生的模态控制力也越大.

对于保留的模态,也就是受控模态,模态控制力越大,代表控制力越强,容易达到较好的控制效果；而对于未考虑的截断模态,由于不需要进行控制,故希望模态控制力越小越好.因此,定义如下所示考虑模态权重比值的最大综合模态控制力评价准则

式中：1≤i≤d1,d1为保留的模态数；1≤j≤d2,d2为截断的模态数；1／ζiωi为第i阶模态的权重,其大小反映了不同阶次模态控制力能所占的比重.

由式（9）可知,Δi越大,受控模态的控制力越大；Δj越小,不予考虑的模态控制力越小；提出的综合考虑模态权重比值的最大模态控制力评价准则的数值也越大,致动器所处位置也越好；当评价准则取最大值时,致动器所处布局位置最优.

3 改进的遗传算法

针对日益出现在各领域中的多种复杂优化问题,一些学者提出采用仿生智能优化算法进行求解.其中,粒子群算法和遗传算法是2种常用而典型的智能优化算法.粒子群算法较为简单、易于实现,然而其理论基础尚未完善、收敛速度较慢,容易陷入局部最优解,从而影响求解精度［15］.

遗传算法具有算法简单、寻优过程自适应和能够并行处理等优点,广泛应用于参数估计、函数优化和控制系统的最优设计等领域.但是传统的遗传算法存在容易早熟收敛和后期搜索效率较低的缺点,为了提高求解精度和算法求解效率,本文采用改进的遗传算法进行求解.

与二进制编码相比,浮点数编码求解精度更高,无需解码,使用起来更为方便.因此,根据数学模型所确定的搜索空间,将致动器位置xasn这一待优化变量,直接组成染色体串进行编码.

与标准遗传算法相比,自适应遗传算法的交叉算子和变异算子可以根据个体适应度值进行相应改变,提高遗传算法的求解效率和收敛能力,因此,交叉算子和变异算子可采用如下公式进行自适应调整［16］：

式中：zmax为种群中最大适应度值,zavg为种群的平均适应度值,z′为可能进行交叉的2个个体中较大的适应度值,z为要变异的个体适应度值；h1、h2、h3、h4∈［0,1］.

4 算例分析

具体的针对贴有n组压电致动器的智能挠性梁结构,如图1所示,挠性梁的长、宽和高分别为Lb、bb和hb,压电致动器的宽和高分别为ba和ha,第n组压电致动器起始和终止位置距梁固定端的距离分别为xasn和xaen.

图1 智能挠性梁模型示意图Fig.1 Model of smart flexible beam

假设挠性梁为Euler-Bernoulli梁模型,同时忽略压电致动器的引入对原挠性梁系统的影响,以n组压电致动器的控制电压作为输入变量,则智能挠性梁的控制矩阵为

φk（x）为一端固定一端自由边界条件下,挠性梁的第k阶模态振型函数,具体表达式如下：

式中：βk为第k阶无量纲弯曲振动频率,由挠性梁频率方程（15）确定.

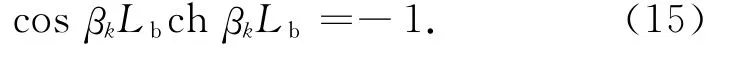
联合控制矩阵Bs和评价准则F,最终建立挠性梁系统致动器优化布局问题的数学模型如下：

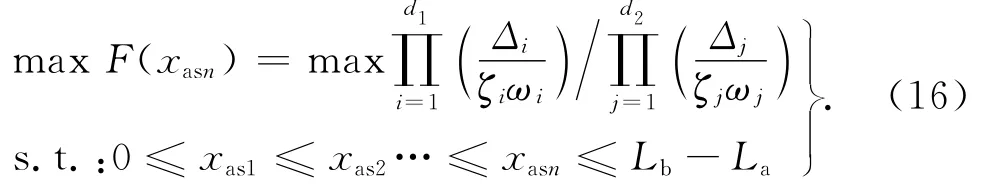
选取挠性梁的几何尺寸Lb、bb和hb分别为620.0、30.0和3.0 mm,Eb＝34.6 GPa,ρb＝1 840 kg／m3.选取压电致动器的La、ba和ha分别为40.0、10.0和0.8 mm,Ea＝117.0 GPa,密度ρa＝7 500 kg／m3,d31＝187×10－12C／N.设定挠性梁的模态阻尼比分别为0.02、0.01和0.006.

考虑到二阶以上的模态对挠性梁系统的输出贡献非常小,首先研究单组压电致动器的优化布局问题,如图2所示给出了单组压电致动器位置与评价准则F之间的对应关系.图2（a）仅仅选取了挠性梁的一阶模态作为保留模态,而图2（b）则选取了挠性梁的前两阶模态作为保留模态.从图2中可以看出,选取的保留模态不同时,致动器位置与评价准则F的关系曲线明显不同,同时将单组压电致动器布局在挠性梁根部时,评价准则F最大,综合模态控制力也最大.

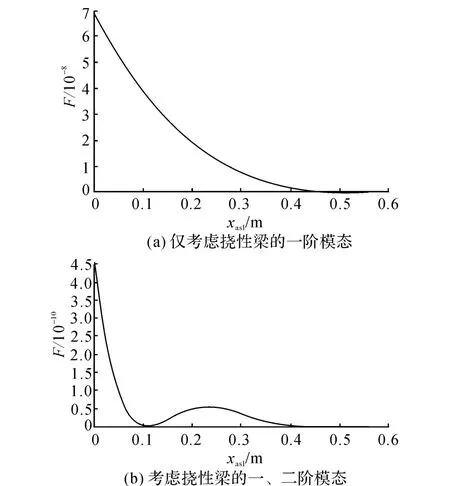
图2 单组致动器位置与评价准则F关系图Fig.2 Relationship between evaluation criteria F and location of single actuator

为了佐证评价准则的普适性,采用改进遗传算法对2组压电致动器的位置进行优化,并与理论计算结果相比较.取挠性梁的前两阶模态作为保留模态,挠性梁的第3阶模态作为截断模态,遗传算法初始参数设置如下：群体规模15,最大进化代数50,遗传优化过程如图3所示,图中G代表进化代数,R代表适应度函数,与评价准则F成倒数关系.由图3可知,适应度函数R在40代左右收敛到最优值.

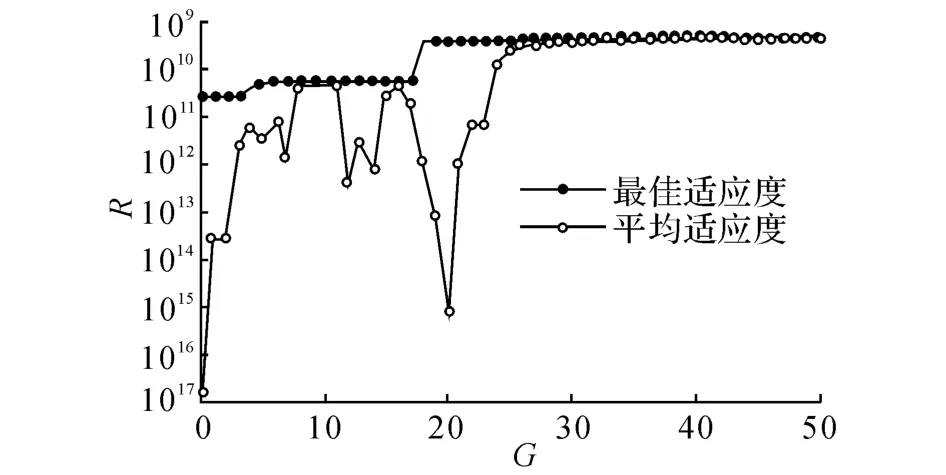
图3 平均及最佳适应度的优化过程Fig.3 Optimization process of mean and best ftness

经过多次优化,当一组压电致动器布局在距挠性梁根部0.004 m处,另一组压电致动器布局在0.278 m处时,F取得最优解.如图4所示给出了多组压电致动器优化布局位置与评价准则的关系曲线,与优化结果对比可知：采用2组压电致动器对挠性梁的前两阶模态进行控制时,一组致动器布局在挠性梁根部,另一组致动器布局在挠性梁中部时,获得的综合模态控制力最大.

图4 多组致动器位置与评价准则F关系图Fig.4 Relationship between evaluation criteria F and location of multiple actuators

5 实验研究

建立如图5所示的智能挠性梁实验系统,挠性梁采用环氧树脂材料制成.根据算例分析结果,并考虑实验布线情况,在距离挠性梁的根部25和280 mm处分别对称地粘贴一组压电致动器（PZT-5型压电材料制成）.为了检测挠性梁的变形,在挠性梁根部粘贴有一组采用半桥接法的应变传感器（电阻应变片,电阻值120Ω,灵敏度系数2.08）.

研制的最大放大倍数5 000的应变放大器,可将挠性梁的弹性变形转换放大为±10 V的电压信号；数据采集卡采用研华科技PCI-1742U多路数据采集卡,可以实现数据A／D、D／A转换；研制的以运算放大器3 583芯片为核心的功率放大器,可将D／A转换后的±10 V电压信号放大输出为±150 V.

实验研究包括模态特性实验、综合模态主动激振实验和冲击信号下的振动控制实验.通过冲击锤敲击激起挠性梁的自由振动,经过计算,得到挠性梁前两阶模态的固有频率和阻尼比的理论值和实验值如表1所示,其中f1、f2分别代表挠性梁的一阶、二阶固有频率,ζ1、ζ2分别代表挠性梁的一阶、二阶模态阻尼比.

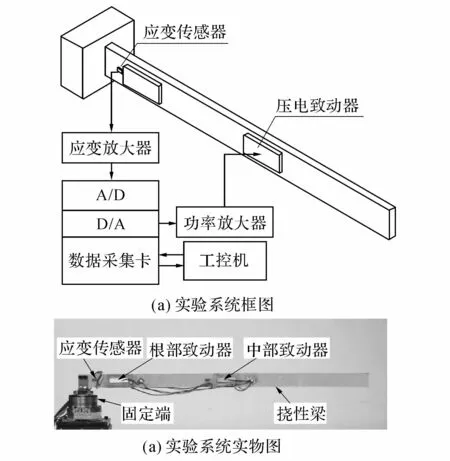
图5 智能挠性梁实验系统Fig.5 Experimental system of smart flexible beam

由表1可知,挠性梁固有频率的实验值与理论值有些差异,为了消除理论计算中忽略的黏结层和材料实际特性等因素对优化结果的影响,需要对优化结果中的致动器的布局效果进行实验验证.

表1 前两阶模态的固有频率和阻尼比Tab.1 Natural frequency and damping ratio of first two modes

对布局在挠性梁根部和中部的压电致动器分别施加16 s的综合模态激励信号为

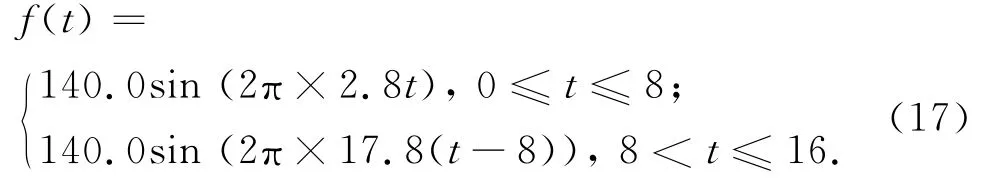
在根部致动器施加综合模态激励信号,粘贴在挠性梁根部的应变传感器的输出信号如图6（a）所示,其中U为传感器时域输出,t为时间；对中部致动器施加相同激励信号后,应变传感器的输出信号如图6（b）所示,2种情况下频域信号的对比情况如图7所示,其中M为传感器频域输出,f为频率.

图6 不同位置致动器激励下应变传感器时域信号Fig.6 Time domain response of strain sensors actuated by piezoelectric actuators in different position

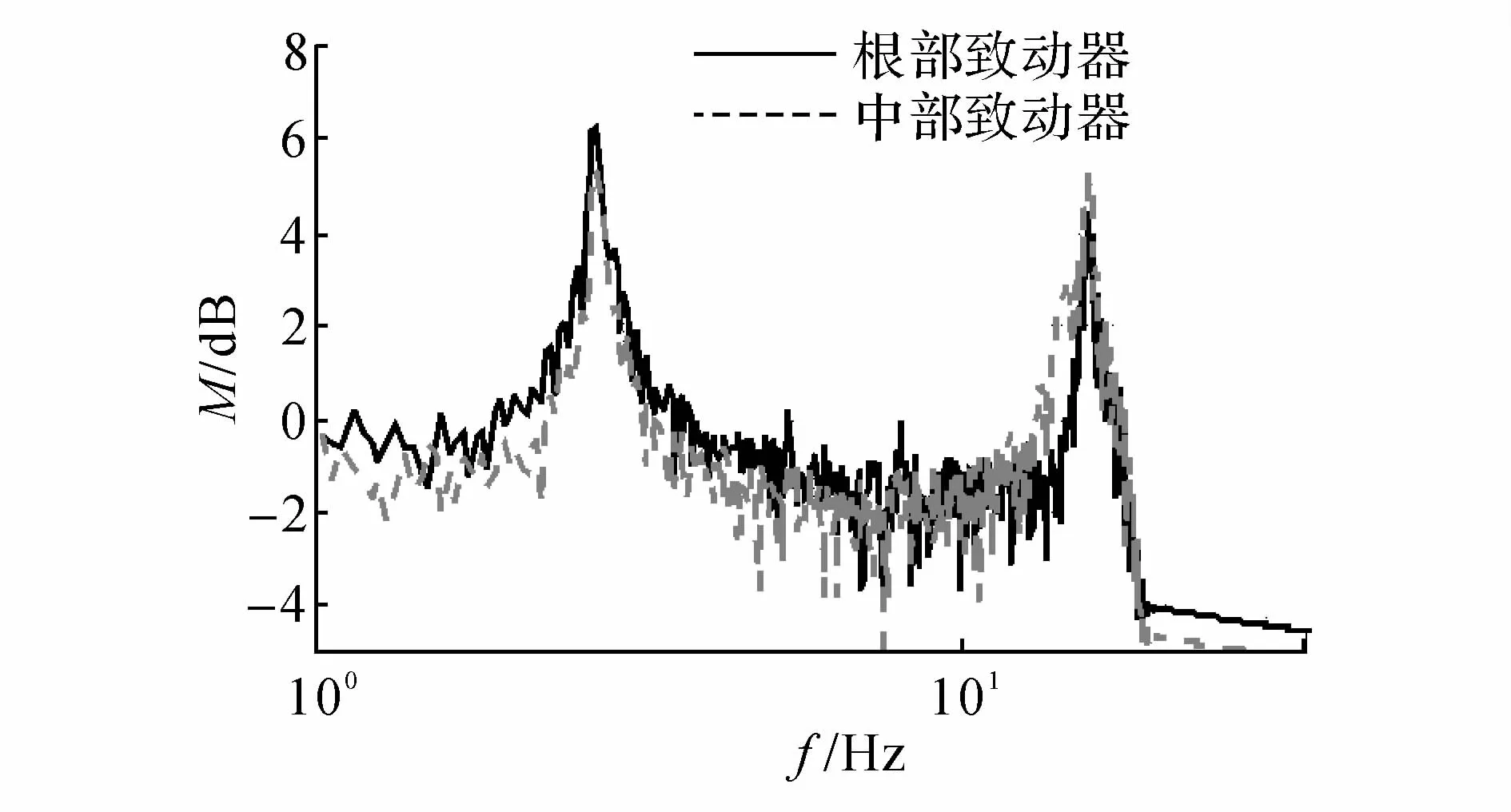
图7 不同位置致动器激励下应变传感器频域信号Fig.7 Frequency response of strain sensors actuated by piezoelectric actuators in different position

图6和7实验结果表明：在综合模态激励信号f（t）的作用下,虽然在10 s以后,布局在挠性梁中部的压电致动器激起的综合模态振动略大,但从总体来看,布局在挠性梁根部的压电致动器激起的综合模态振动更大,这说明对于挠性梁的综合模态振动,单组压电致动器布局在根部比布局在中部时,致动能力更强,综合模态控制力也更大.

如图8所示给出了经模态提取后得到的挠性梁一阶模态响应.实验结果表明：在相同激励信号作用下,布局在挠性梁根部的压电致动器激起的一阶模态振动更大；这说明对于挠性梁的一阶模态振动,单组压电致动器布局在根部时比布局在中部时,致动能力更强,一阶模态控制力也更大.而对于挠性梁系统,其一阶模态占主导地位,因而根部致动器的综合模态控制力也更大.

图8 不同位置致动器激励下挠性梁的一阶模态响应Fig.8 Response of first mode of beam actuated by piezoelectric actuators in different position

为了从控制效果的角度来比较不同布局位置下压电致动器的控制性能,在挠性梁的中部施加一冲击激励信号,并采用负反馈控制对挠性梁的振动进行抑制,如图9所示给出了利用布局在挠性梁根部、中部的压电致动器进行振动抑制的实际控制效果曲线,从图中可以看出,根部和中部压电致动器均能较为有效地抑制挠性梁的振动,但根部致动器的控制效果明显要优于中部,因此,当采用单组压电致动器时,将压电致动器布局在挠性梁根部,所获得的综合模态控制力更大.

如图10所示给出了仅利用根部压电致动器和同时利用根部、中部压电致动器进行振动抑制的实际控制效果曲线,从图中可以看出,同时利用根部、中部压电致动器的控制效果要优于仅利用根部压电致动器,因此,当采用2组压电致动器时,一组布局在挠性梁根部,另一组布局在挠性梁中部时,所获得的综合模态控制力更大.

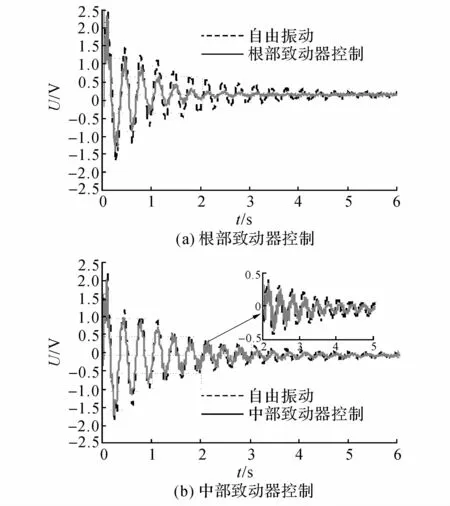
图9 单组致动器控制时应变传感器的时域信号Fig.9 Time domain response of strain sensors for single actuator

图10 单组与多组致动器控制时的应变片传感器的时域信号Fig.10 Time domain response of strain sensors for single and multiple actuators

综上,对比实验结果和算例分析可知：在相同激励信号下,当采用单组压电致动器时,将致动器布局在挠性梁根部时,获得的综合模态控制力最大,当采用多组压电致动器时,分别将其布局在挠性梁根部和中部时,所获得的综合模态控制力更大,与算例分析结果一致.

6 结 语

采用提出的表征最大综合模态控制力的评价准则,对智能挠性结构中致动器的优化布局问题进行了研究,理论分析和实验结果表明：采用优化结果中的致动器布局位置时,系统具有更好的综合模态控制力,振动抑制效果也更优,所提出的评价准则和优化方法是可行的.虽然文中选择的梁为简单的挠性梁结构,但研究方法可以延伸到其他复杂的智能挠性板壳结构上,从而丰富了致动器优化布局的方法.

（References）：

［1］RAMOS F,FELIU V,PAYO I.Design of trajectories with physical constraints for very lightweight single link flexible arms［J］.Journal of Vibration and Control, 2008,14（8）：1091-1110.

［2］朱灯林,吕蕊,俞洁.压电智能悬臂梁的压电片位置、尺寸及控制融合优化设计［J］.机械工程学报,2009,45（2）：262-267.

ZHU Deng-lin,LV Rui,YU Jie.Integrated optimal design of the PZT position,size and control of smart cantilever beam［J］.Chinese Journal of Mechanical Engineering,2009,45（2）：262-267.

［3］魏燕定,娄军强,吕永桂,等.振动主动控制中性二次型最优控制问题研究［J］.浙江大学学报：工学版,2009, 43（3）：420-424.

WEI Yan-ding,LOU Jun-qiang,LV Yong-gui,et al.Research on linear quadratic optimal control problem in active vibration control［J］.Journal of Zhejiang University：Engineering Science,2009,43（3）：420-424.

［4］HU Q L,MA G F.Vibration control of flexible spacecraft actuated by piezoceramics via variable structure strategy［J］.Journal of Harbin Institute of Technology, 2007,14（5）：604-608.

［5］DUTTA R,GANGULI R,MANI V.Swarm intelligence algorithms for integrated optimization of piezoelectric actuator and sensor placement and feedback gains［J］.Smart Materials&Structures,2011,20（10501810）：1-14.

［6］GURSES K,BUCKHAM B J,PARK E J.Vibration control of a single-link flexible manipulator using an array of fiber optic curvature sensors and PZT actuators［J］.Mechatronics,2009,19（2）：167-177.

［7］钱锋,王建国,汪权,等.基于模态应变能分布的压电致动器／传感器位置优化遗传算法［J］.振动与冲击, 2013,32（11）：161-166.

QIAN Feng,WANG Jian-guo,WANG Quan,et al.Optimal placement of piezoelectric actuator／sensor using genetic algorithm based on modal strain energy distribution［J］.Journal of Vibration and Shock,2013,32（11）：161-166.

［8］LINDBERG R E,LONGMAN R W.On the number and placement of actuators for independent model space control［J］.Journal of Guidance,Control,and Dynamics,1984,7（2）：215-221.

［9］AMBROSIO P,RESTA F,RIPAMONTI F.An H2norm approach for the actuator and sensor placement in vibration control of a smart structure［J］.Smart Materials and Structures,2012,21（12）：125016.

［10］邱志成.挠性板振动抑制的敏感器与驱动器优化配置［J］.宇航学报,2002,23（4）：30-36.

QIU Zhi-cheng.Optimal placement of sensors and actuators for flexible plate of vibration suppression［J］.Journal of Astronautics,2002,23（4）：30-36.

［11］BRUANT I,PROSLIER L.Optimal location of actuators and sensors in active vibration control［J］.Journal of Intelligent Material Systems and Structures,2005,16（3）：197-206.

［12］NESTOROVIC T,TRAJKOV M.Optimal actuator and sensor placement based on balanced reduced models［J］.Mechanical Systems and Signal Processing, 2013,36（2）：271-289.

［13］SUN D,MILLS J K,SHAN J,et al.A PZT actuator control of a single-link flexible manipulator based on linear velocity feedback and actuator placement［J］.Mechatronics,2004,14（4）：381-401.

［14］WANG Q,WANG C M.A controllability index for optimal design of piezoelectric actuators in vibration control of beam structures［J］.Journal of Sound and Vibration,2001,242（3）：507-518.

［15］BIGLAR M,MIRDAMADI H R,DANESH M.Optimal locations and orientations of piezoelectric transducers on cylindrical shell based on gramians of contributed and undesired Rayleigh-Ritz modes using genetic algorithm［J］.Journal of Sound and Vibration,2014, 333（5）：1224-1244.

［16］SRINIVAS M,PATNAIK L M.Adaptive probabilities of crossover and mutation in genetic algorithms［J］.Systems, Man and Cybernetics,1994,24（4）：656-667.

Optimal placement of piezoelectric actuators using synthetic modal control force

YANG Yi-ling1,LOU Jun-qiang2,WEI Yan-ding1,FU Lei1,TIAN Geng1,ZHAO Xiao-wei1
（1.Institute of Manufacturing Engineering,Key Laboratory of Advanced Manufacturing Technology of Zhejiang Province,Zhejiang University,Hangzhou 310027,China；2.College of Mechanical Engineering and Mechanics,Ningbo University,Ningbo 315211,China）

This paper dealt with the optimal placement of actuators in smart flexible structures.Based on the analysis of dynamic equations and state space equations of flexible structures,the modal theory was adopted and the singular value decomposition of control matrices was employed.Then,a criterion of the maximum synthetic modal control force was proposed.The criterion involved the effect of reserved and residual modes to the modal control force.Meanwhile,modal weights were considered.Finally,a flexible beam with piezoelectric actuators／strain sensors was chosen as an example,theoretical calculations and the improved genetic algorithm were used for the optimal analysis.Thus,the optimal positions of piezoelectric actuators with maximum synthetic modal control force were found,and an experimental system was set up to verify the proposed method.The experimental results demonstrate that the system has a good synthetic modal control force and control effect by using the optimal placement result of actuators.The proposed evaluation criterion and optimal method is feasible.

smart flexible structures；synthetic modal control force；piezoelectric actuators；optimal placement

10.3785／j.issn.1008-973X.2015.05.005

TP 24；TH 113

A

1008-973X（2015）05-0841-07

2014-10-17. 浙江大学学报（工学版）网址：www.journals.zju.edu.cn／eng

国家自然科学基金资助项目（51375433）；浙江省自然科学基金资助项目（LY13E050008）.

杨依领（1987－）,男,博士生,从事振动主动控制、压电应用等方面研究.E-mail：meyangyl＠zju.edu.cn

魏燕定,男,教授.E-mail：weiyd＠zju.edu.cn