机器人末端位移传感器的安装位置标定方法
袁康正,朱伟东,陈 磊,薛 雷,戚文刚
(1.浙江大学机械工程学系,浙江杭州310027;2.上海飞机制造有限公司,上海200436)
机器人末端位移传感器的安装位置标定方法
袁康正1,朱伟东1,陈 磊2,薛 雷2,戚文刚2
(1.浙江大学机械工程学系,浙江杭州310027;2.上海飞机制造有限公司,上海200436)
针对机器人末端激光位移传感器位置的标定问题,基于平面和球面模板拟合的标定模型,设计一种同时标定位移传感器方向和位置参数的标定方法.以机器人离线编程与机器人运动学仿真为基础,对2种标定算法进行系统的仿真对比实验.分析影响2种标定模板标定精度的影响因素,如传感器测量误差、测量长度以及标定参数数量.引入可观测指数来评价机器人运动空间中测量姿态的标定效率.通过优化算法计算得出一组近似最优测量姿态以及最佳评价指数,减少非建模误差以及测量误差对标定结果的影响,有效地提高算法的抵抗噪声能力、标定精度以及标定效率.实验结果表明,使用该标定方法标定后的位置参数标准差为0.37 mm,方向参数标准差为0.35°.
机器人TCP标定;激光位移传感器;最小二乘法;可观测指数
将激光位移传感器、激光扫描仪、照相机等非接触式测量设备安装于机器人末端法兰盘上,构成对环境具有一定感知功能的智能机器人是机器人的主要发展趋势[1].对于在法兰上装有传感器设备的机器人,传感器相对于法兰盘的位置和方向需要事先标定,这一过程称为机器人刀尖点标定(tool center point,TCP)[2].另外,随着机器人仿真和离线编程技术在工业中的应用日益增加[3],为了更加有效地使用机器人离线编程,需要进行准确的机器人标定和机器人TCP标定.
国内外对机器人TCP标定问题的研究已经取得较大进展,但主要是用于解决机器人与工业相机、3D扫描仪之间的标定问题.Shiu等[4]通过四元代数法和线性最小二乘法来分步求解相机位姿的旋转矩阵和平移矩阵.Li等[5-6]以标准球作为标定对象,并通过机器人的平移运动和旋转运动分步求解扫描仪与机器人之间的旋转和平移矩阵.而针对机器人末端执行器夹持激光位移传感器的TCP标定问题,目前采取的方法主要是通过求解机器人在特定几何约束(点、线、面)下的闭环运动链方程[2].王胜华等[1]采用多次改变机器人位姿对同一点进行测量,利用运动学方程和最小二乘原理求出机器人末端坐标系与传感器坐标系之间的齐次变换矩阵.此标定方法很难保证每次测量点都在同一点上,且标定结果受实验环境、实验操作影响较大.吴聊等[7]采用基于平面模板的标定方法,在不同位姿下对平面进行测量,利用非线性最小二乘法拟合平面求解标定问题.该方法虽然能够快速标定出结果,但是参数分布对结果影响较大,因此标定精度受实验操作影响.Zhu等[8]提出了基于球面拟合的标定算法,标定精度较高.但该方法首先需要机器人视觉伺服控制系统辅助标定位移传感器方向参数,不具有通用性.Awei等[9]通过设计圆柱面和锥面复合标定对象,提出了一种串联坐标测量机标定以及TCP标定新算法.卢科青等[10]通过设计一种方向可调的标定面,在三坐标测量机平台上对点激光测头激光束方向进行了标定.这2种方法虽然能满足标定精度的要求,但标定过程往往需要将位移传感器的方向和位置参数分步标定,标定过程较为繁琐,而且需要复杂的标定对象或者精密的辅助测量设备,标定成本高.同时,在位移传感器标定过程中,机器人的测量姿态和测量条件对标定结果的影响很大,而国内外学者在姿态选择问题上研究较少,使得标定算法的移植性较差.
为了实现TCP标定算法的快速性和通用性,本文在非线性最小二乘优化算法的基础上,建立了基于平面和球面拟合的标定理论模型,对位移传感器的方向和位置参数进行同时标定,简化了标定步骤.通过引入可观测指数和优化算法得出最优测量姿态以及最佳评价指数,提高了算法的抗干扰能力、标定精度和标定效率.
1 标定数学模型
1.1 平面标定模型
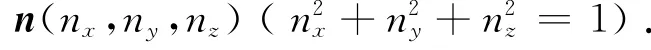

图1 平面标定模型Fig.1 Calibration model based on plane
测量点在法兰坐标系XtYtZtOt下的坐标x可以表示为

式中:x=[x,y,z]T,x0=[x0,y0,z0]T,n=[nx,ny,nz]T.
测量点在机器人base坐标系下的坐标为pw(xw,yw,zw).由法兰盘和机器人base坐标系之间齐次变换关系可得

由于测量点在固定板平面上,因此pw满足平面方程:

联立方程(2)、(3)可得位移传感器测量点到平面的距离为

操作机器人到不同的位姿进行测量,获取m组测量结果,可得di=fi(x0,y0,z0,α,β,a,b,c)(i=1,2,….,m),其中(cosα=nx,cosβ=ny).即可以通过非线性最小二乘法求解待标定参数,问题转化为求解如下最小二乘问题:
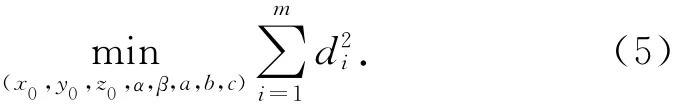
1.2 球面标定模型
与平面拟合标定模型相似,球面拟合标定模型如图2所示.测量点pw(xw,yw,zw)在已知半径R的固定球面上,满足空间球面方程:
联立方程(2)、(6)可得到测量点到球心pc(xc,yc, zc)的距离为


图2 球面标定模型Fig.2 Calibration model based on sphere
通过控制机器人使激光位移传感器在不同姿态下测量球面上m个点,可以得到m个形式如式(7)的等式.则位移传感器标定问题即为求解非线性最小二乘问题:

2 仿真分析
针对建立的平面和球面标定模型,在三维设计软件CATIA中建立相应的三维模型并在拟合面上选取若干个离散测量点.通过离线编程前置处理软件提取测量点信息并导入到DELMIA软件中的离线编程模块进行机器人测量仿真,获取机器人法兰位姿矩阵T以及测量长度l数据,仿真实验平台如图3所示.在测量值l上添加均匀分布噪声来近似模拟机器人运动误差、传感器测量误差、拟合面误差等因素对测量值的影响.最后,非线性最小二乘问题可通过数值分析软件MATLAB中Levenberg-Marquardt算法求解[11].
2.1 2种标定算法标定结果对比
分别在l上添加随机测量误差±Δε,对2种标定算法进行多次优化实验.2种标定算法标定的传感器参考点位置绝对误差Δd和激光束方向角度绝对误差Δθ与Δε的关系如图4(a)和(b)所示.
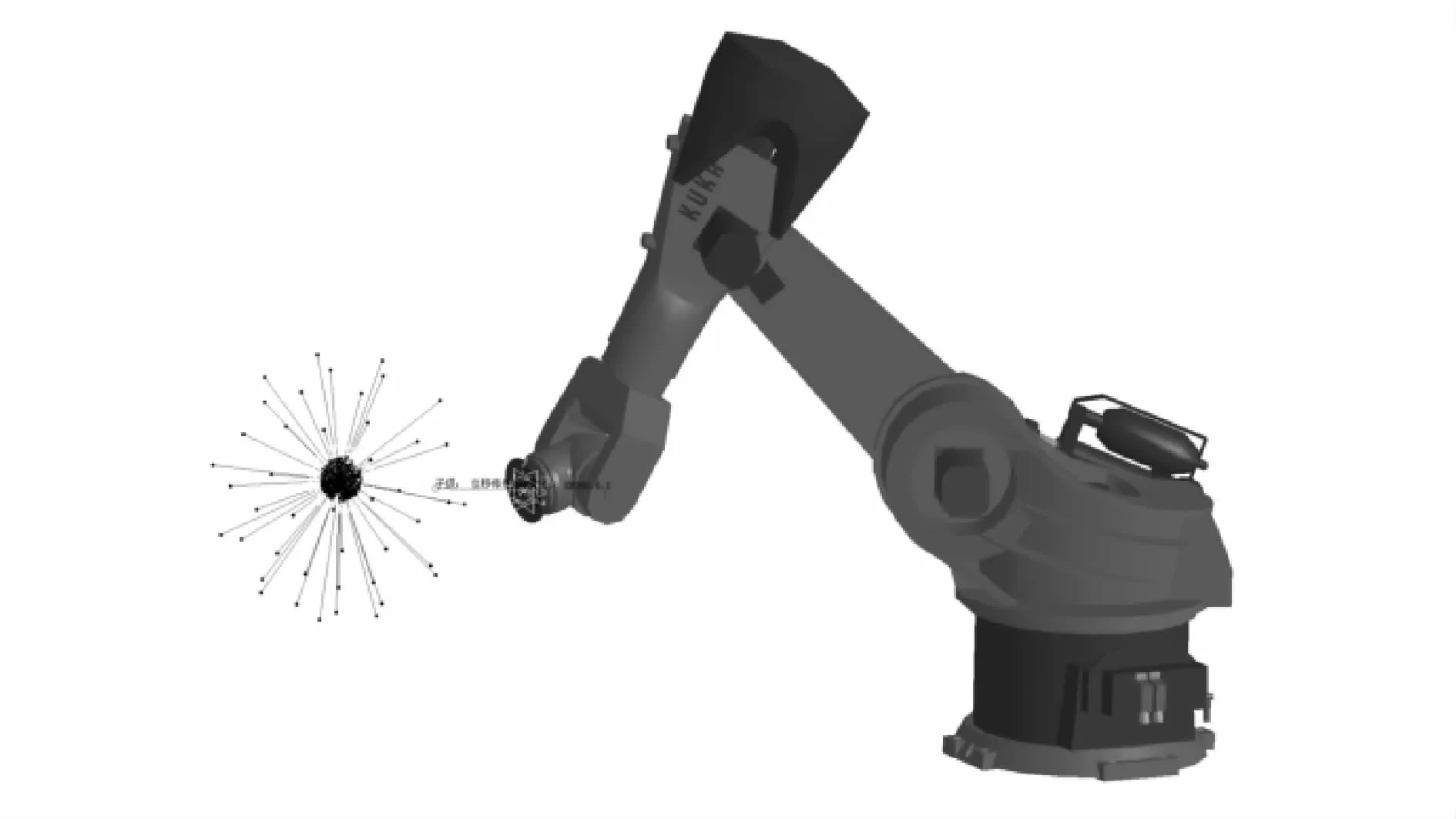
图3 仿真分析实验平台Fig.3 Experimental platform for simulation analysis
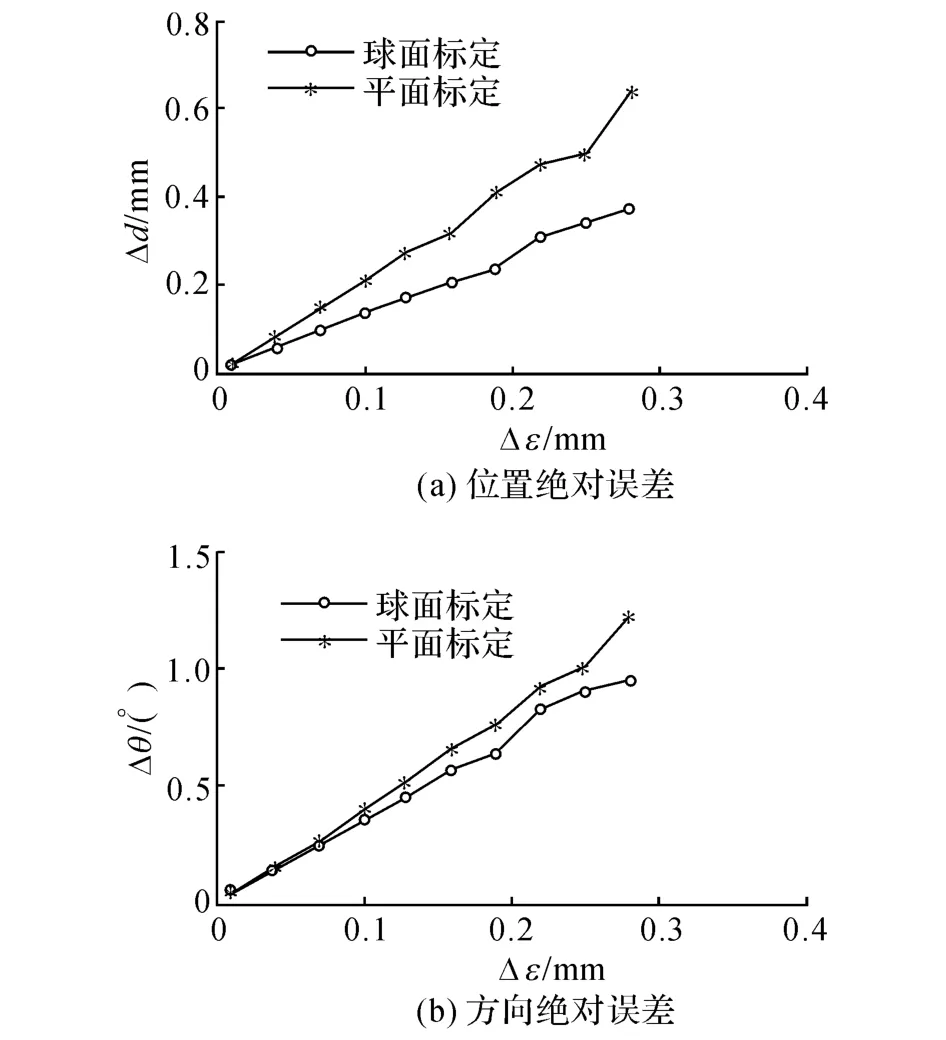
图4 不同噪声情况下2种标定算法的标定结果对比Fig.4 Comparison of calibration results of two calibration algorithms with varied noise
在Δε=±0.2 mm的噪声等级下,分别对平面和球面标定算法随机进行2 000次优化计算,位置绝对误差Δd和方向角度绝对误差Δθ的直方图如图5所示,其中f为频率数.从仿真结果图4和5可知,球面算法与平面算法相比,球面算法的标定精度高、收敛性好,且误差越大效果越明显.
2.2 参数影响仿真分析
测量长度:针对球面标定算法,分析了位移传感器测量值分布情况对标定结果的影响.在传感器测量位置、方向相同,噪声大小相同,测量长度l均值¯l分别为20、40、60、80、100 mm条件下进行优化计算.5种情况下的标定结果如图6所示.
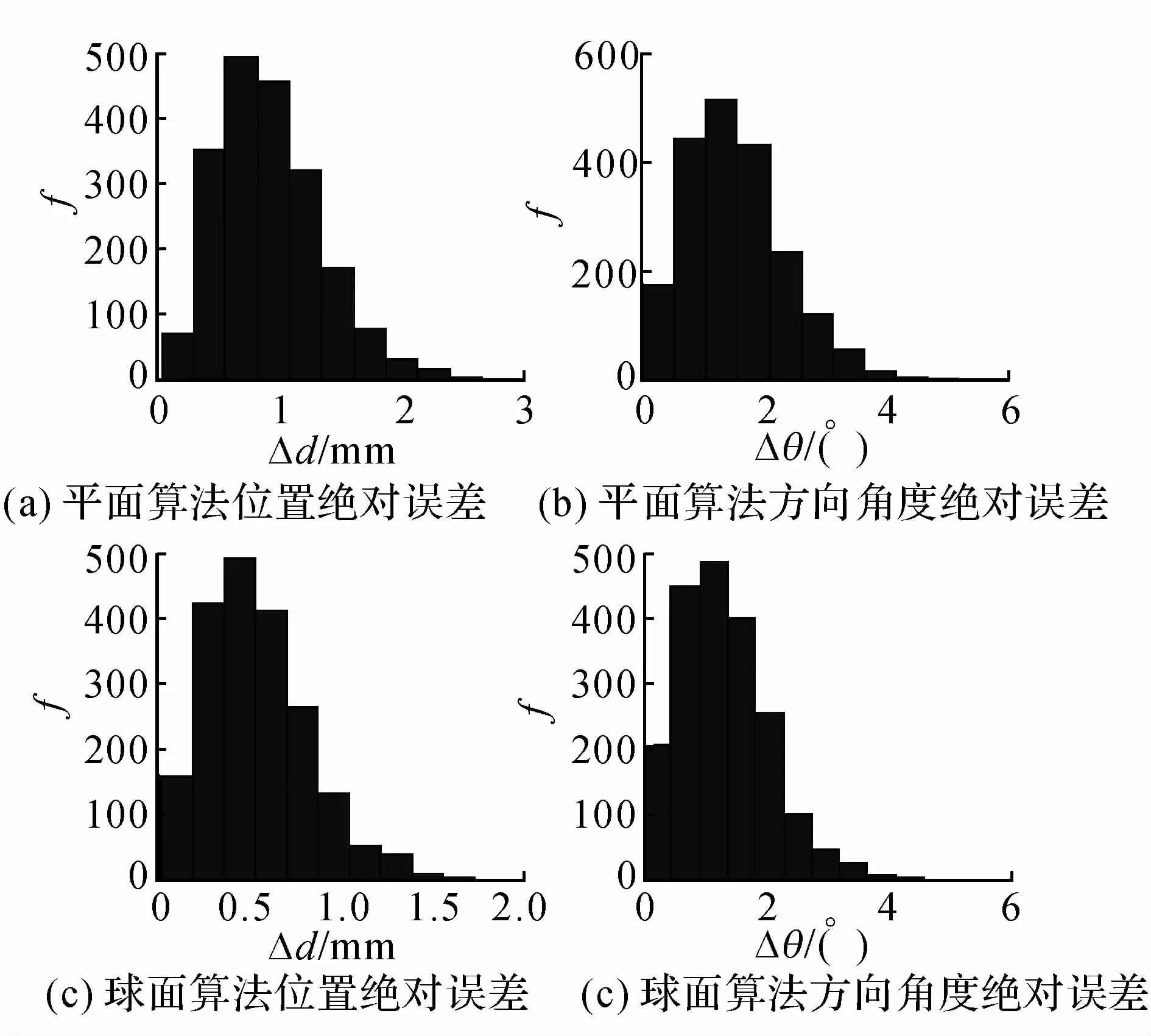
图5 2种算法的优化结果Fig.5 Optimization results of two calibration algorlthms
标定参数个数:针对球面标定算法,位移传感器需标定的参数个数n对位置标定精度影响较大.在所有参数都未知的情况下,此时标定参数个数n=8(传感器位置、方向、球心位置).若球心在机器人base下坐标已知,则需要标定参数个数n=5.若传感器方向参数事先通过其他方法标定,此时需要标定参数个数n=6.在不同标定参数个数下,球面算法的位置标定误差和噪声误差的关系如图7所示.
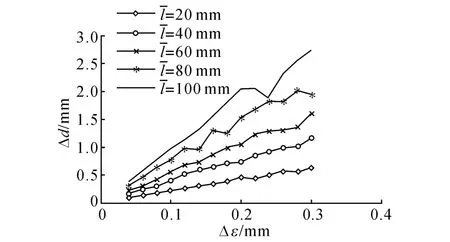
图6 不同测量长度下的标定误差Fig.6 Calibration errors with different measuring distances
2.3 姿态仿真优化
针对图2球面标定理论模型,可得

式中:ω为待标定参数(x,y,z,α,β,xc,yc,zc),ε为传感器测量误差、机器人运动误差等引起的测量点到球心距离误差.将上式对T进行微分可得

式中:ΔF为函数误差,J为雅克比辨识矩阵,ΔT为机器人姿态矩阵误差,对J进行奇异值分解可得
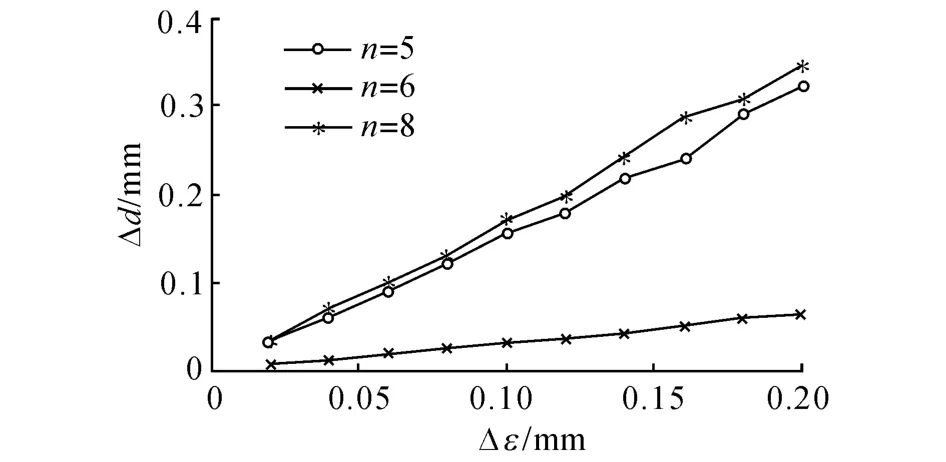
图7 参数个数对标定误差的影响Fig.7 Influence of the number of optimized parameters on calibration error

式中:U、V为正交矩阵,Σ为对角矩阵,对角元素为σi(i=1,…,m),其中σ1≥σ2…≥σm≥0.

可观测指数[12]基于雅克比辨识矩阵的奇异值分解,量化在特定位姿下参数辨识的可观测性.指数数值越大,则位置误差对于参数误差的贡献越大,即未建模误差和测量误差的影响越小[13].
5种可观测指数定义如下:

最优姿态优化算法流程如下:
1)在机器人测量运动空间内随机选取足够多的N组测量姿态作为候选姿态.
2)在候选姿态中选取n(n<N)组姿态作为初始标定姿态集合,用Ω表示.
3)从余下的(N-n)组候选姿态中,选取一个姿态ξ+增加到Ω,使得增加后的标定姿态Ω+1的可观测指数与Ω相比增加最大.
4)从Ω+1中去掉一个姿态ξ-,使得去掉后的标定姿态Ω可观测指数减小最少.
5)重复步骤3和4直到ξ+与ξ-相等.
由仿真模型获取N=2 000组候选姿态,分别应用5种可观测指数对候选姿态进行优化计算.5种可观测指数优化前后对比如图8所示.

图8 5种可观测指数优化结果Fig.8 Optimization results of five OIs
2.4 仿真结论
由仿真实验结果可以得出以下结论:球面标定算法比平面算法收敛性好,且标定精度高.在实验条件允许情况下,方向参数通过辅助设备单独标定,能够有效地提高球面算法的标定精度,而球心坐标参数在已知的情况下对传感器位置标定精度的提高不大.在测量姿态相同的情况下,传感器的测距越小位置参数标定精度越高.5种可观测指数优化姿态在一定程度上均能提高球面标定算法的稳定性和精度,其中O5指数优化效果最好.
3 机器人制孔系统测量实验

图9 实验平台Fig.9 Experiment platform
为了检验球面标定算法的有效性,进行了基于球面拟合的位移传感器标定实验,实验平台如图9所示.实验中采用KUKA KR360-2型号六自由度机器人,重复定位精度±0.08 mm.机器人法兰末端执行器上安装由Baumer公司生产的ch-8501型号激光位移传感器,最大测距120 mm,分辨率0.01 mm,线性误差0.08 mm.固定的标定球采用直径为30 mm的标准球,其球面圆度0.08μm.
通过改变机器人姿态使激光位移传感器对标定球面进行30次测量,并记录相关数据.将待标定参数的粗略测量值作为迭代计算的初始值,通过Matlab优化工具箱中lsqnonlin函数,求解球面标定模型中的非线性最小二乘问题.采用球面算法求解参数的优化结果如表1所示.位移传感器位置参数标准差为0.37 mm,接近传统视觉测量方法标定精度(标准差为0.2 mm)[8].

表1 基于球面标定模型激光位移传感器标定结果Tab.1 Calibration results of laser displacement sensor with calibration model based on sphere
4 结 语
本文详细分析了基于平面和球面拟合的位移传感器标定理论模型,并通过仿真分析对比得出球面模板方法在收敛性和标定精度上要优于平面模板方法.为了避免使用额外的附加测量设备,本文同时标定位移传感器方向和位置参数,简化了标定流程.为了减小传感器测量误差和测量姿态对球面标定算法的精度、稳定性和标定效率的影响,本文引入了可观测指数对标定姿态进行评价,进而获得最优姿态.实验结果显示,采用本文的标定方法,激光位移传感器的标定结果位置参数最大标准差为0.37 mm,方向参数最大标准差0.35°,接近传统视觉测量方法标定精度.
(References):
[1]王胜华,都东,张文增,等.机器人定点变位姿手-眼标定方法[J].清华大学学报:自然科学版,2007,47(2):165-168.
WANG Sheng-hua,DU Dong,ZHANG Wen-zeng,et al.Hand-eye calibration for the robot by measuring a fixed point from different poses[J].Journal of Tsinghua University:Science and Technology,2007,47(2):165-168.
[2]GAN Z,TANG Q.Visual sensing and its applications: integration of laser sensors to industrial robots[M].Hangzhou:Zhejiang University Press,2011.
[3]MITSI S,BOUZAKIS K D,MANSOUR G,et al.Offline programming of an industrial robot for manufacturing[J].The International Journal of Advanced Manufacturing Technology,2005,26(3):262-267.
[4]SHIU Y C,AHMAD S.Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX=XB[J].Robotics and Automation,IEEE Transactions on,1989,5(1):16-29.
[5]LI J,ZHU J,DUAN K,et al.Calibration of a portable laser 3-D scanner used by a robot and its use in measurement[J].Optical Engineering,2008,47(1):017202-017202-8.
[6]REN Y J,YIN S B,ZHU J G.Calibration technology in application of robot-laser scanning system[J].Optical Engineering,2012,51(11):114204-114204.
[7]吴聊,杨向东,蓝善清,等.基于平面模板的机器人TCF标定[J].机器人,2012,34(1):98-103.
WU Liao,YANG Xiang-dong,LAN Shan-qing,et al.Robotic TCF calibration based on a planar template[J].Robot,2012,34(1):98-103.
[8]ZHU Z,TANG Q,LI J,et al.Calibration of laser displacement sensor used by industrial robots[J].Optical Engineering,2004,43(1):12-13.
[9]ZHOU A,GUO J,SHAO W,et al.A segmental calibration method for a miniature serial-link coordinate measuring machine using a compound calibration artefact[J].Measurement Science and Technology,2013,24(6):065001.
[10]卢科青,王文,陈子辰.点激光测头激光束方向标定[J].光学精密工程,2010,18(4):880-886.
LU Ke-qing,WANG Wen,CHEN Zi-chen.Calibration of laser beam-direction for point laser sensors[J].Optics and Precision Engineering,2010,18(4):880-886.
[11]陈淑铭,乔田田.一个求解非线性最小二乘问题的新方法[J].烟台大学学报:自然科学与工程版,2004,01:14 -22.
CHEN Shu-ming,QIAO Tian-tian.A new method of solving problem of nonlinear least square[J].Journal of Yantai University:Natural Science and Engineering Edition,2004,17(1):14-22.
[12]SUN Y,HOLLERBACH J M.Observability index selection for robot calibration[C]//IEEE International Conference on Robotics and Automation.Pasadena:IEEE,2008:831-836.
[13]JOUBAIR A,BONEV I A.Comparison of the efficiency of five observability indices for robot calibration[J].Mechanism and Machine Theory,2013,70:254-265.
Approach for calibrating position of displacement sensor mounted on robot end-effector
YUAN Kang-zheng1,ZHU Wei-dong1,CHEN Lei2,XUE Lei2,QI Wen-gang2
(1.Department of Mechanical Engineering,Zhejiang University,Hangzhou 310027,China;2.Shanghai Aircraft Manufacturing Limited Company,Shanghai 200436,China)
In order to calibrate the position and orientation of laser displacement sensors mounted on a robot,an approach was devised for calibrating the position and orientation parameters simultaneously,based on the model of plane and sphere fitting.A contrast experiment was proposed and conducted systematically based on robot off-line programming and robot kinematics simulation.Effects on the accuracy of the two calibration algorithm were also analyzed such as the measurement error,length of sensor and the number of calibration parameters.Observability indices were introduced to evaluate the efficiency of parameter identification with the measurement configurations in robot motion space.Optimal measurement configurations and best evaluation index were calculated using on optimization algorithm.The effects of the nonmodeling error and measurement error are reduced.The stability,accuracy and efficiency of the algorithm are improved.Experiment results of our improved calibration algorithm indicate that the standard deviation of position is 0.37 mm,the standard deviation of orientation is 0.35°.
robot TCP calibration;laser displacement sensor;least square method;observability index
10.3785/j.issn.1008-973X.2015.05.003
TP 242
A
1008-973X(2015)05-0829-06
2014-05-20. 浙江大学学报(工学版)网址:www.journals.zju.edu.cn/eng
国家自然科学基金资助项目(51205352).
袁康正(1990-),男,硕士,从事机器人精密制孔、视觉测量等研究.E-mail:441090246@163.com.
朱伟东,男,副教授.E-mail:wdzhu@zju.edu.cn.
下期论文摘要预登

