基于方差平方根CKF算法在鱼雷跟踪中的应用

刘清慧，　高　江，　邓南明

（中国人民解放军91388部队， 广东 湛江， 524022）

基于方差平方根CKF算法在鱼雷跟踪中的应用

刘清慧，高江，邓南明

（中国人民解放军91388部队， 广东 湛江， 524022）

针对现有无迹卡尔曼滤波（UKF）算法在高维系统中易出现协方差非正定导致滤波不稳定甚至发散的问题，探讨了基于方差平方根的容积卡尔曼滤波（CKF）算法在鱼雷目标跟踪中的应用。该算法首先基于Cubature准则，获得一组具有相同权重的Cubature点， 然后经过非线性系统方程将该点集进行转换产生新的点， 以此预测下一时刻系统的状态， 并在滤波更新过程中通过传播状态的方差平方根， 确保了方差矩阵的对称性和正定性。仿真结果表明， CKF的滤波精度要高于UKF。

鱼雷； 目标跟踪； 方差平方根； 无迹卡尔曼滤波； 容积卡尔曼滤波

0　引言

鱼雷作为一种现代化的水中武器， 是水面舰艇和潜艇面临的主要水下威胁。对来袭鱼雷目标进行跟踪识别， 是反鱼雷技术需解决的首要难题，现有技术仅靠鱼雷报警声呐测得的纯方位信息难以实现对鱼雷目标的精确定位跟踪［1-2］。

为此， 很多学者提出了基于鱼雷的运动学模型以及鱼雷报警声呐测得的信息， 构造鱼雷目标跟踪的状态空间模型， 并建立可应用于该模型的滤波算法， 以提高鱼雷目标跟踪精度， 实现对目标状态准确估计。扩展卡尔曼滤波（extend Kalman filter， EKF）是最早在工程中实现运用的非线性滤波算法［3］， 其主要思想是利用1阶泰勒级数将非线性系统方程模型在滤波状态预测值处进行展开，从而使得线性化系统模型仍能应用于线性卡尔曼滤波中， 但是在强非线性模型下高阶项的忽略会使得EKF滤波估计精度不高， 同时非线性函数泰勒级数展开中雅克比矩阵的求取， 使得EKF算法计算量增大， 复杂度提高［4］。

基于此， Julier和Uhlman基于无迹变换（unscented transformation， UT）思想， 提出了一种新的滤波算法——无迹卡尔曼滤波（unscented Kalman filter， UKF）［5］。它通过具有不同权值的2n+1个确定性Sigma采样点， 并利用上述Sigma点经过非线性系统方程转换后产生新的点来估计下一时刻系统状态的均值和方差， 理论推导证明UKF滤波估计精度能够达到非线性系统泰勒级数展开的3阶项， 因此UKF精度高于EKF， 计算量却与EKF相同。但是， UKF中Sigma点集的选取缺乏数学推导依据， 且在高维数系统中UKF的Sigma点权值容易出现负值， 导致滤波过程中的协方差矩阵非正定， 出现滤波数值不稳定性，致使算法中断运行。

为了克服UKF算法中存在的问题， 很多学者开始研究数学推导更为严谨的容积卡尔曼滤波（cubature Kalman filter， CKF）［6］。CKF算法依据理论依据更为严格的Cubature准则获得2n个同等权值的Cubature点， 同样利用这些点来估计下一时刻系统状态。

文中针对鱼雷目标跟踪问题， 在CKF的基础上通过利用状态的方差平方根替代方差在滤波过程中计算， 确保方差矩阵的对称性和正定性， 解决了UKF在非线性估计中易出现协方差非正定导致滤波不稳定甚至发散的问题。最后利用CKF算法与UKF算法进行仿真对比分析， 结果表明CKF算法的滤波精度要高于UKF。

1　高斯滤波器的一般形式

假设系统离散非线性系统模型［7］

式中： F和H为已知任意函数； x为系统状态向量； z为量测向量； v和w分别为系统噪声和量测噪声， 均满足零均值高斯分布， 即

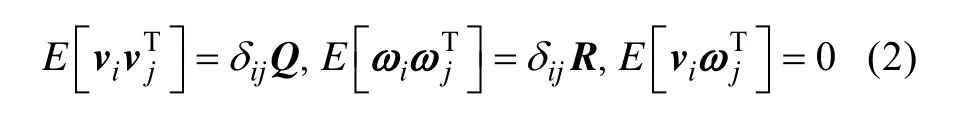
贝叶斯滤波是应用广泛的估计算法， 根据系统的观测序列矢量Zk-1=｛z，…，z｝迭代计算系

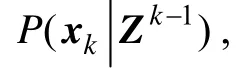
1） 时间更新

其中， d为积分符号。

2） 观测更新

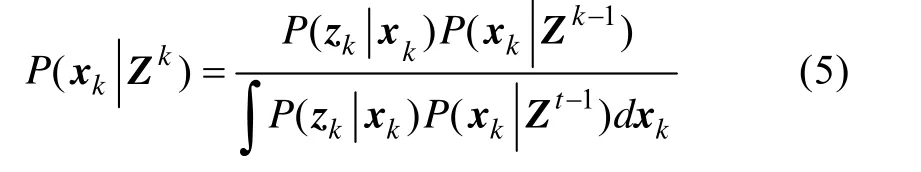
2　UKF算法

UKF算法的核心思想是UT变换。该算法首先进行UT变换将系统状态离散成一组Simga点集，然后利用此点集计算式（2）～式（5）得到滤波算法， 每个滤波周期内进行时间更新和量测更新。根据上述分析， 得UKF算法的简要步骤如下。

1） 初始化

2） 计算Sigma点集（k=1，2，…）

继续求解上述Sigma点各自相应的权值为

式中， n和κ必须满足

3） 时间更新

4） 再次计算Sigma点集（k=1，2，…）

5） 观测更新

从而可得状态估计值和状态误差协方差估计值分别为

以上即为UKF算法的计算步骤。从上述分析可知， UKF中Sigma点集的选取缺乏严格数学推导依据， 且从式（9）可知， 当系统维数（维数n≥4）较高时， UKF中的自由调节参数κ将会小于零， 又据式（4）可知， 某些Sigma点的权值也将小于零， UKF滤波过程中的协方差非正定， 从而导致滤波数值不稳定性， 出现算法中断运行情况发生。

3　基于方差平方根的CKF算法

针对UKF算法缺乏严格数学推导的不足， 文中提出把CKF算法应用在鱼雷目标跟踪中。该算法根据理论依据更为严格的Cubature准则， 通过2n个同等权值的Cubature点经非线性系统方程转换后产生新的点来给出下一时刻系统状态的预测， 与UKF相同， CKF算法也不需对非线性模型线性化， 但是CKF算法比UKF算法使用的采用点更少。同时， 文中在滤波过程中利用状态的方差平方根来替代方差完成算法的迭代运算， 确保了方差矩阵的对称性和正定性， 解决了UKF在非线性估计中协方差出现非正定的问题。

根据上述分析， 可得基于方差平方根的CKF算法的简要步骤如下。

文奇的“奇点”理论提出后，并没有立即获得人们的广泛认同，只是得到一部分人的支持，如库兹韦尔。库兹韦尔于1990年出版《智能机器时代》(The Age of Intelligent Machines)一书，认为随着计算机性能的不断提升，未来经过足够多的时间，人类将会创造比他自身更聪明的实体[27]。库兹威尔的推断是基于计算能力的指数级增长及技术的加速循环规则。

3） 基于Spherical-Radial Cubature准则， 计算Cubature点集ξi（i=1，2，…）及其权值

其中， ［1］i表示单位矩阵的第i列。

4） 时间更新

5） 利用Cholesky分解误差协方差

6） 再次计算Cubature点集ξi（i=1，2，…）及其权值

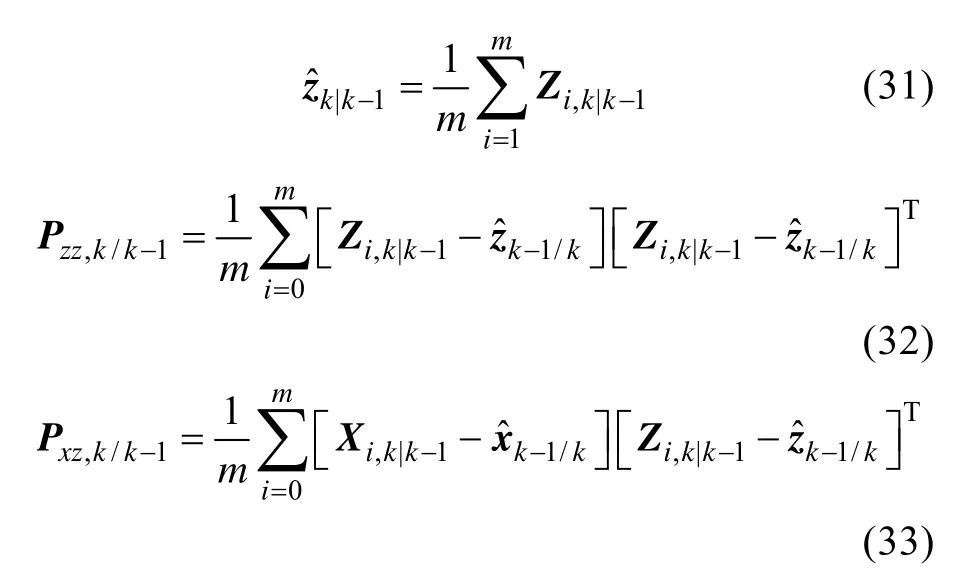
根据以上式子， 可得基于方差平方根的CKF算法的增益

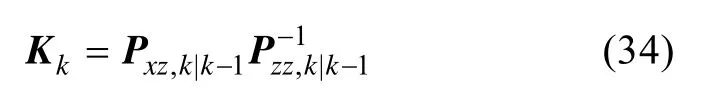
从而可得状态估计值和状态误差协方差估计值分别为

以上即为CKF算法的计算步骤。从上述分析可知， CKF与UKF的滤波过程类似， 都是通过一组具有权重的点集经过非线性转换来计算系统状态的预测， 其优点是不仅避免了线性化处理非线性模型， 而且不局限于系统模型的具体非线性方程。同时， CKF具有比UKF更优越的滤波性能。首先， CKF因其经过严格的Cubature准则数学推导， 所以在理论上有一定的保证； 其次， 由式（23）可知， Cubature点集的权值均为1/m， 该值始终大于0， 提高了滤波的数值稳定性和滤波精度； 最后CKF再利用式（22）和式（28）， 确保了CKF算法中协方差的正定性， 解决了UKF在高维系统中存在的问题， 实现了滤波器建立的优化设计。

4　仿真结果与性能分析

利用Matlab软件平台对上述方差平方根的CKF算法以及UKF算法进行仿真验证， 假设鱼雷目标的非线性运动学方程［8］

同时， 仿真试验中假设鱼雷报警声呐对鱼雷目标进行测量， 设两者斜距为r， 方位角为θ， 则鱼雷跟踪模型的量测方程［8］

同时， 设置系统的真实初始值

仿真时间200 s， 进行50次Monte Carlo仿真。采用均方根误差（root mean square error， RMSE）来评估UKF和EKF算法的估计效果方法。定义k时刻位置、速度和角速度的均方根误差

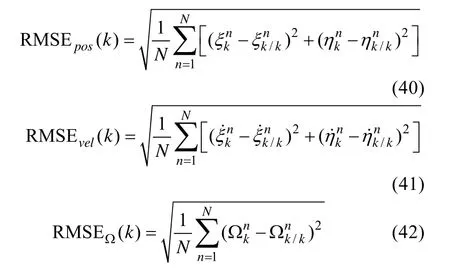
其中， N为Monte Carlo仿真次数。

图1～图3分别给出了50次Monte Carlo位置、速度和角速度的仿真结果。从图中可知， UKF误差曲线在开始的0～50 s中没有结果输出， 这是由于系统状态维数n=5， 根据式（9）可知， UKF的自由调节参数κ=-2， 从而导致某些Sigma点权值出现负值， 进一步导致协方差矩阵的非正当，造成算法中断运行， UKF滤波估计无结果输出。同时可知， 基于方差平方根的CKF算法由于利用状态的方差平方根来替代方差完成算法的迭代运算， 确保了方差矩阵的对称性和正定性， 故CKF滤波估计结果曲线没有出现算法中断现象， 虽然由于系统噪声和观测噪声的存在， 使得基于方差平方根的CKF误差曲线存在振荡情况， 但是都能稳定在一定范围内， 达到了滤波估计效果。

图1　基于容积卡尔曼滤波算法和无迹卡尔曼滤波算法得到的位置均方根误差曲线Fig. 1　Curves of root mean square error(RMSE) of position versus time with cubature Kalman filter (CKF) algorthm and unscented Kalman filter (UKF) algorthm

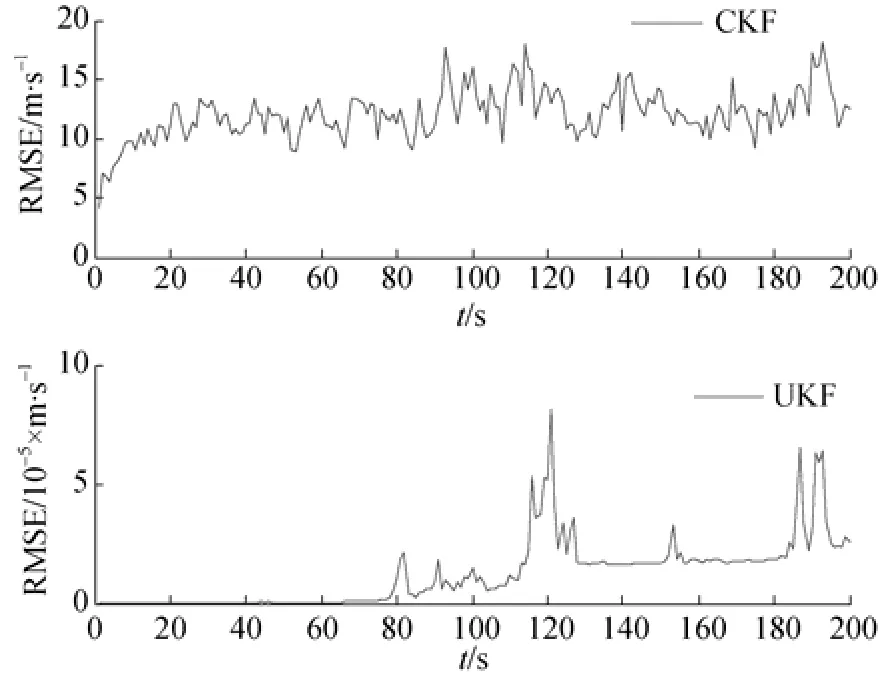
图2　基于CKF和UKF算法得到的速度均方根误差Fig. 2　Curves of RMSE of velocity versus time with CKF algorthm and UKF algorthm

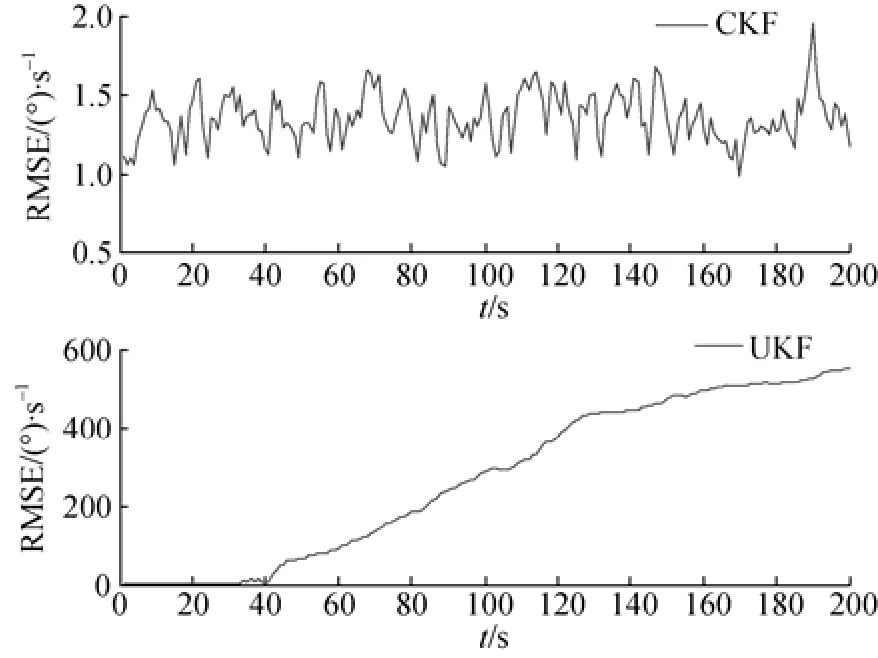
图3　基于CKF和UKF算法的角速度均方根误差曲线Fig. 3　Curves of RMSE of angular velocity versus time with CKF algorthm and UKF algorthm

综上所述， 无论是在滤波稳定性以及收敛精度上CKF都远远优于UKF， 因此证实了CKF算法性能上优于UKF。

5　结束语

针对于鱼雷目标跟踪问题， 文中提出了基于方差平方根的CKF算法， 将该算法滤波性能与UKF算法进行比较， 并进行了仿真试验验证。通过仿真结果分析可知， CKF算法估计精度优于UKF算法。文中的研究对工程实际应用具有一定的参考价值。

［1］ 陈敬军. 国外反舰鱼雷的现状与发展趋势［J］. 声学技术， 2013， 32（2）： 164-170.

Chen Jing-jun. The Status Quo and Development Trend of Overseas Anti-surface Ship Torpedo［J］. Technical Acoustics， 2013， 32（2）： 164-170.

［2］ 肖碧琴， 袁富宇， 苗艳. 鱼雷目标定位跟踪技术［J］. 火力与指挥控制， 2014， 39（1）： 103-105.

Xiao Bi-qin， Yuan Fu-yu， Miao Yan. Review of Localization Algorithms for Torpedo-Target［J］. Fire Control & Command Control， 2014， 39（1）： 103-105.

［3］ Athans M， Wishner R P， Bertolini A. Suboptimal State Estimation for Continuous Time Nonlinear Systems from Discrete Noisy Measurements［J］. IEEE Transactions on Automatic Control， 1968， 5（13）： 504-514.

［4］ Kalman R E. A New Approach to Linear Filtering and Pediction Poblems［J］. Journal of Basic Engineering， 1960，1（82）： 34-45.

［5］ Julier S J， Uhlman J K. A New Extension of the Kalman Filter to Nonlinear Systems［J］. Proceedings of the Society of Photo-Optical Instrumentation Engineers， 1997， 3068（1）： 182-193.

［6］ Arasaratnam I， Haykin S. Cubature Kalman Filters［J］. IEEE Transactions on Automatic Control， 2009， 54（6）：1254-1269.

［7］ 占荣辉， 张军. 非线性滤波理论与目标跟踪应用［M］.北京： 国防工业出版社， 2013： 256-257.

［8］ 高文娟， 李亚安， 陈晓， 等. 基于交互式多模型的水下机动目标跟踪［J］. 鱼雷技术， 2015， 23（3）： 196-201.

Gao Wen-juan， Li Ya-an， Chen Xiao， et al. Application of IMM to Underwater Maneuver Target Tracking［J］. Torpedo Technology， 2015， 23（3）： 196-201.

（责任编辑： 杨力军）

Application of CKF Algorithm Based on Square Root
of Variance to Torpedo Tracking

LIU Qing-hui，GAO Jiang，DENG Nan-ming
（91388thUnit， The People′s Liberation Army of China， Zhanjiang 524022， China）

The existing unscented Kalman filter（UKF） algorithm results in non-definite covariance easily in high-dimensional system， which leads to instability of filter and even divergence. In this paper， the application of cubature Kalman filter（CKF） algorithm based on square root of variances to underwater target tracking is discussed. This algorithm can achieve a group of cubature points with same weight based on the cubature principle， transform the points set into the new points by non-linear system equation in order to predict the system state at next time， and ensure symmetry and positive definiteness of the covariance matrix by using the square root of the variances of propagation state. Simulation results show that CKF is better than UKF in estimation precision.

torpedo； target tracking； square root of variance； unscented Kalman filter（UKF）； cubature Kalman filter（CKF）

TJ630.34； TN953

A

1673-1948（2015）06-0428-05

10.11993/j.issn.1673-1948.2015.06.007

2015-09-06；

2015-10-30.

刘清慧（1974-）， 男， 硕士， 工程师， 主要从事水中兵器试验研究.