水下航行器释放机构动作可靠性分析

周　炜，　薛　来，　赵　敏

（1. 海军驻昆明七五〇试验场军事代表室， 云南 昆明， 650051； 2. 昆明船舶设备研究试验中心， 云南， 昆明，650051）

水下航行器释放机构动作可靠性分析

周炜1，薛来2，赵敏2

（1. 海军驻昆明七五〇试验场军事代表室， 云南 昆明， 650051； 2. 昆明船舶设备研究试验中心， 云南， 昆明，650051）

水下航行器的释放机构是该装备的重要组成部分， 释放机构能否正常动作， 是该装备完成作战任务的关键。该文以验算点法为依据， 利用FREET机械可靠性分析软件分析了释放机构关键组成部件的可靠性， 所得结论为水下航行器释放机构的设计提供参考。

水下航行器； 机械可靠性； 释放机构； 验算点法

0　引言

水下航行器的舱体设计有一个释放机构， 其功能是在航行器发射一定时间后在水中打开舱体舱盖， 舱体内的组件在负浮力作用下脱离舱体完成作战任务。该机构主要组成零件包括锁定机构、动力产生装置、连杆、转轴及曲柄， 当释放机构启动时，首先是锁定机构解锁， 然后动力装置产生驱动力使连杆运动， 连杆固定在转轴一端带动转轴转动， 固定在另一端的曲柄在转轴转动下运动， 从而将舱盖打开， 完成释放动作。释放机构是水下航行器的重要组成部分， 其能否正常动作是水下航行器完成作战任务的关键。释放机构的可靠性设计通常采用安全系数法， 由于该方法有很大的盲目性和保守性［1］，导致设计结果存在不合理之处。文章基于验算点法建立了释放机构可靠性计算模型， 利用FREET软件对现有释放机构的可靠性进行计算分析， 得出其可靠度， 通过分析结果可有效指导设计。

1　理论依据

1.1机械可靠性计算模型

机械产品进行可靠性设计分析时， 根据其设计功能建立相对应的状态函数g（X）， 当g（X）可看作只有广义应力r和广义强度l两个随机变量时

机械产品在任意时刻是否能够保持其规定功能， 在数学上可用状态函数的取值是否大于0来决定， 把产品状态分为可靠状态（用g（X）＞0表示）和失效状态（用g（X）＜0表示）， 而产品可靠状态向失效状态转换的临界状态（用g（X）=0表示）称为极限状态， g（X）=0称为极限状态方程。在解析几何中， 极限状态方程是坐标系中的一个多维曲面，称为极限状态曲面［2］。

在机械可靠性中， 常用可靠度指标β代替可靠度， 它被定义为状态函数的均值与标准差之比， 即

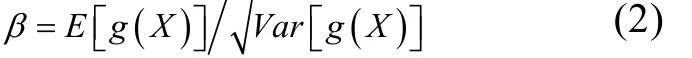
当基本随机变量均服从正态分布， 且状态方程为基本变量的线性函数时， 可靠度为

其中， Φ（·）为标准正态分布函数。

1.2一次二阶矩法

一次二阶矩（first order second moment， FOSM）法在机械结构可靠性领域得到了广泛应用， 经过几十年的研究发展已成为世界各国结构安全标准、规范的基础。验算点法是FOSM法的一种， 在1974年由Hasofer和Lind提出［3］， 他们将可靠性指标β定义为标准正态空间内坐标原点到极限状态曲面的最短距离， 并将最短距离在极限状态面对应当点定义为设计验算点（most probabile point， MPP）使得对应于同一失效面建立失效方程的不同表达式可得唯一可靠性指标。验算点法能够考虑非正态随机变量， 在计算工作量差不多的条件下， 可对可靠度指标进行精度较高的近似计算。具体算法如下。

1） 假定初始验算点

2） 根据设计验算点， 计算非正态随机变量的等效正态分布参数；

3） 计算可靠度指标

4） 计算重要度系数

5） 计算新的验算点

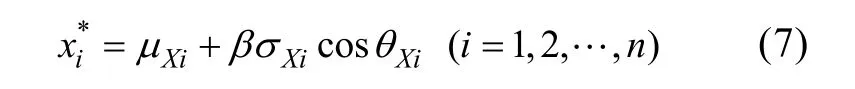
1.3FREET机械可靠性软件

FREET（feasible reliability engineering tool）软件用于对简单与复杂机械结构产品进行统计分析及可靠性和敏感性分析。该软件的特点是在精度要求约束下有效减少仿真样本量， 使设计人员定义的工程问题能以相对简单快速的方法进行评估，可极大减少设计人员的计算时间。FREET可自定义状态方程， 计算可靠度所用方法为验算点法。

2　释放机构可靠性计算模型

2.1释放机构组成

释放机构主要由曲柄、转轴、连杆及锁定机构构成， 如图1所示。

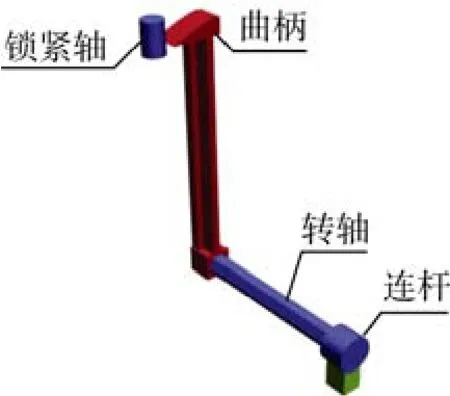
图1　释放机构示意图Fig. 1　Schematic of releasing device

曲柄负责将气源驱动下转轴的旋转动作传递给舱盖， 实现释放机构舱盖的打开与关闭。转轴负责在连杆驱动下旋转， 带动舱盖运动， 实现释放机构舱盖的打开与关闭。连杆负责将气源产生装置产生的动力传递给转轴， 将直线运动转变为转轴的旋转运动。释放机构设计有锁定机构， 安装好机构内待释放组件并关闭舱盖后， 对释放机构进行锁定， 开舱前要先解锁， 才能打开舱盖，避免舱盖在发射气流（或水流）冲击下产生误动作。舱盖关闭后， 其外形与航行器壳体外表面共形， 可减小航行阻力。

2.2状态方程

2.2.1曲柄

对曲柄进行受力分析后， 确定曲柄的主要受力为拉伸应力。曲柄材料采用06Cr19Ni10， 其截面如图2所示。则曲柄的拉伸应力为

式中： ε为拉伸应力； F为拉力最大值； a1， b1， c， h为曲柄截面尺寸。

根据应力-强度干涉理论， 以应力极限状态表示的状态方程为

其中， r1为曲柄材料强度。

2.2.2转轴

对转轴进行受力分析后， 确定转轴的主要受力为扭转应力。转轴材料采用06Cr19Ni10， 其截面可近似正八角形（见图3）。则转轴所受的扭转应力

式中： τ为转轴承受的扭转应力； T为扭矩； a2为八角形厚度。

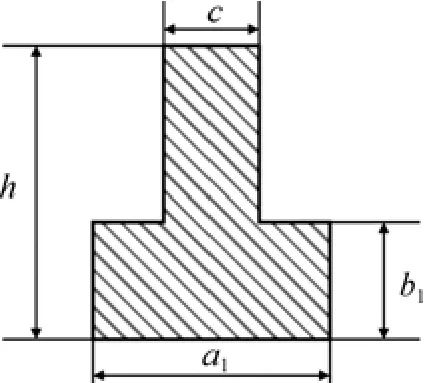
图2　曲柄截面图Fig. 2　Section of crank

　图3　转轴截面图Fig. 3　Section of shaft

根据应力-强度干涉理论， 以应力极限状态表示的状态方程为

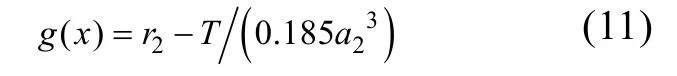
其中， r2为转轴材料强度。

2.2.3连杆

对连杆进行受力分析后， 确定转轴的主要受力为剪切应力。连杆材料采用45号碳素钢， 其截面为矩形， 见图4。则连杆所受的剪切应力为

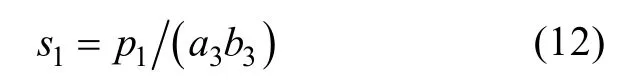
式中： s1为连杆剪切应力； p1为连杆承受的剪切载荷； a3为连杆截面宽度； b3为连杆的截面厚度。

根据应力-强度干涉理论， 以应力极限状态表示的状态方程为

式中： r3为转轴材料剪切强度。

2.2.4锁定机构

对锁紧装置进行受力分析后， 确定装置的主要受力零件锁紧轴的受力为剪切应力。锁紧轴材料采用06Cr19Ni10， 其截面为圆形， 如图5所示。则锁紧轴的剪切应力为

式中： s2为锁紧轴剪切应力； p2为锁紧轴承受的剪切载荷； d为锁紧轴截面直径； n为剪切面数。

图4　连杆截面图Fig. 4　Section of connecting rod

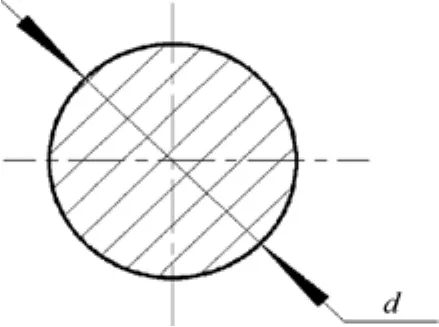
图5　锁紧轴截面图Fig. 5　Section of clamp　axis

根据应力-强度干涉理论， 以应力极限状态表示的状态方程为

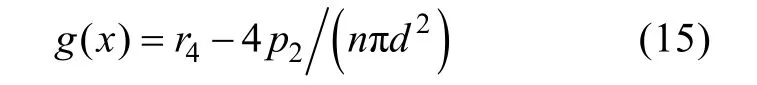
式中： r4为锁紧轴材料剪切强度。

3　释放机构可靠度计算

3.1设计参数数据的统计处理

为简化计算， 假设基本随机变量相互独立且服从正态分布， 这是因为正态分布能反映多数零部件的实际情况， 并且即使当强度与应力均为非正态分布时， 若采用正态分布假设， 一般将得到偏于保守的结果［1］。

3.2各部分可靠度计算

释放机构中任一部分发生失效， 整个机构均不能正常工作， 因此认为释放机构的可靠性模型为串联模型， 则释放机构的可靠度为

计算得释放机构可靠度约为1.000。

表1　释放机构各部件的参数及可靠度计算结果Table 1　Parameters and calculated reliabilities of releasing device′s components

4　计算结果分析

经计算释放机构可靠度约为1.000， 而实际上该机构的可靠度规定值为0.99， 可以看出其设计较为保守。对释放机构的各组件重新进行可靠性设计， 得出了当释放机构各组件可靠度达到0.999 9时的设计参数， 并计算出按新的设计参数计算出的机构减少的质量， 如表2所示。从表2可以看出， 原本各组件尺寸设计过大， 导致质量的增加以及不必要的材料浪费。

表2　释放机构各部件的可靠性设计结果Table 2　Designed reliabilities of releasing device′s components

5　结束语

文章在基本随机参数的概率特性已知情况下，应用验算点法对现有释放机构可靠度进行计算，找出释放机构可靠性设计的不足， 通过上述各零件可靠度分析可知， 采用可靠性设计结果与常规设计相比， 能极大的节省材料， 降低产品质量，但从计算过程可知， 要保证这一高可靠度必须使材料的强度和应力的均值、标准差保持稳定不变，即可靠性设计的先进性是要以材料制造工艺的稳定性及对载荷测定的准确性为前提条件。各零件的可靠性设计中还进行了敏感分析， 以便在今后的设计中注意控制那些影响显著的参数。文中提供的可靠性分析方法对水下航行器机械零件设计的指导具有通用性， 可以在未来水下航行器的可靠性设计中加以应用。

［1］ 刘惟信. 机械可靠性设计［M］. 北京： 清华大学出版社，1996.

［2］ 张建国， 苏多， 刘英卫. 机械产品可靠性分析与优化［M］. 北京： 电子工业出版社， 2008.

［3］ Hasofer A M， Lind N C. An Exact and Invariant First Order Reliability Format［J］. Journal of Engineering Mechanics， 1974， 100（EMI）： 111-121.

［4］ Zotos J. Mathematical Modeling of the Chemical， Mechanical and Physical Properties of Engineering Alloys［M］. Massachusetts Toronto： D.C. Health and Company Lexington， 1977.

（责任编辑： 陈曦）

Mechanical Reliability Analysis of Releasing Device for Underwater Vehicle

ZHOU Wei1，XUE Lai2，ZHAO Min2
（1. Navy Representative Office Stationed in Kunming 750 Test Range， Kunming 650051， China； 2. Kunming Shipborne Equipment Research & Test Center， Kunming 650051， China）

Whether an underwater vehicle can complete its mission depends on the normal operation of its releasing device. In this paper， the mechanical reliability analysis software FREET is employed to analyze the reliability of the key components of the releasing device with the JC method. The results obtained may be a reference for further design of an underwater vehicle.

underwater vehicle； mechanical reliability； releasing device； JC method

TJ630

A

1673-1948（2015）06-0410-04

10.11993/j.issn.1673-1948.2015.06.003

2015-07-26；

2015-09-13.

周炜（1979-）， 男， 工程师， 研究方向为水中兵器研制过程管理方法.