任意阵型下分层海底空时混响建模与仿真

赵栋良，　梁　红，　杨长生，　郑亚宁

（西北工业大学 航海学院， 陕西 西安， 710072）

任意阵型下分层海底空时混响建模与仿真

赵栋良，梁红，杨长生，郑亚宁

（西北工业大学 航海学院， 陕西 西安， 710072）

针对实际海底环境的分层介质特性， 建立了一种适用于任意阵型的分层海底空时混响模型。充分考虑了多普勒频移、散射体方位、海底沉积层与基层的不均匀性、以及海水与沉积层界面对混响形成的影响， 将所有散射信号在接收阵元处叠加， 得到单通道混响的输出， 从而建立了更加符合复杂海底环境的混响空时模型。以连续波（CW）信号作为发射信号对建立的混响模型进行了仿真， 所得到混响的时域特性和2D空时特性符合理论分析，验证了该海底空时混响模型的有效性和准确性。

海底混响; 任意阵型; 分层海底; 空时模型

0　引言

混响作为声呐主动工作方式下的特有干扰，一直是水声信号处理的难题。混响建模与仿真是进行水下声信号处理中的一个重要组成部分， 国内外学者已对海洋混响的建模与仿真做了大量研究［1-3］， 但随着水下信号处理新技术的出现和应用， 在各类复杂的环境下， 现有的一些混响模型和仿真方法已不能满足研究的需求， 因此对海洋混响的建模与仿真技术也提出了更高的要求。

实测结果表明， 浅海海底散射强度远大于体积散射强度和海面散射强度， 所以海底混响是主动声呐工作的主要背景干扰之一。

现有的大部分混响空时模型如随机点散射累积模型、网格模型等［4-6］， 在建立的时候一般只在单一阵型下考虑海底界面散射对混响的影响， 并没有充分考虑其他阵型和海底沉积层的不均匀性对混响的贡献， 而实际在混响产生过程中， 复杂的海底环境对混响有很大的影响， 这使得现有的很多模型不能够准确反映实际的海底混响并且在阵型选择上具有很大的局限性。

文章针对实际海底介质环境和其对混响的显著影响， 全面考虑了多普勒频移、散射体的方位、海底沉积层内不均匀粒子、沉积层介质的变化以及沉积层界面对混响的共同作用， 建立了一种符合分层海底环境且可以满足阵元在空间位置上任意配置的海底空时混响模型， 利用所建立的模型，对混响的频谱特性、瞬时值分布、包络值分布以及空时特性进行验证， 仿真结果符合实际要求。

1　海底混响的空时2D分布

如图1所示， 声呐运动平台距海底距离为h，保持匀速直线运动， 速度为V， 方向沿x轴正方向， 发射波长为λ， 散射体相对于y轴方向的入射锥角为α， 相对于速度方向的入射方位角为φ，相对于xoy面的夹角为俯仰角θ。于是海底某散射单元的多普勒频移

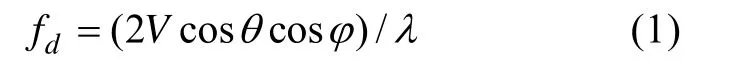
图1　基阵与散射单元的几何关系Fig. 1　Geometry of array and scatterering cell

由图1可知， cosα=sinφcosθ ， 将此关系式代入式（1）可得

式中： fdmax=2V/λ为最大多普勒频移。当θ一定， fd和cosα的关系为圆方程。实际上主动声呐基阵只向前辐射声能， 所以实际的混响空时2D分布是1个半圆； 如果平台静止， 则fdmax=fd=0，混响的多普勒频率在空时2D分布为存在于零频的一条直线， 如图2所示。由于界面散射体随机起伏造成的多普勒展宽， 在不考虑运动平台自身多普勒抑制的情况下， 使得运动平台混响分布应为环状， 静止平台混响分布应为条状。

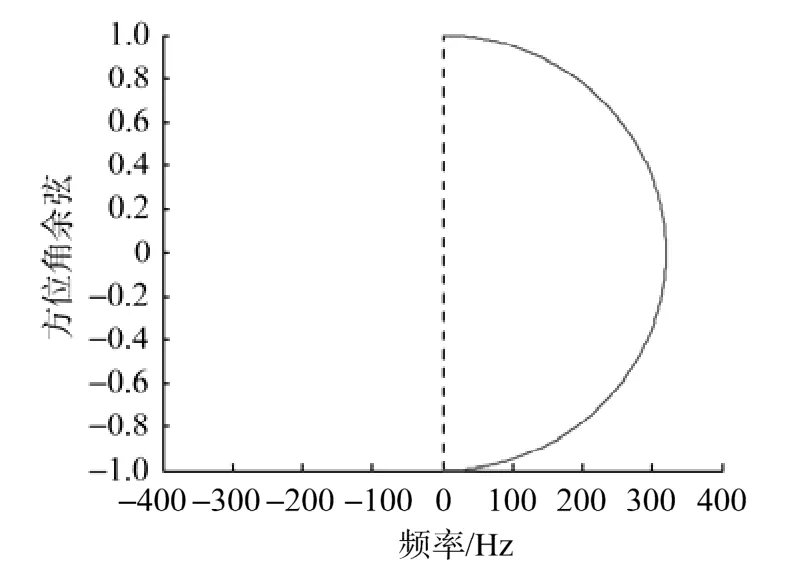
图2　混响空时分布图Fig. 2　Distribution of Space-time distribution of reverberation

2　任意阵型下分层海底混响空时建模

2.1散射体分布及散射单元的划分

由于散射体到声源的距离各不相同， 所以在某一时刻海底界面上对混响有贡献的区域为圆环状， 散射体海底分布如图3所示。假设声呐阵元已经加挡， 不考虑后向辐射， 所以散射元仅分布在阵列的前方。

图3　海底散射体分佈Fig. 3　Distribution of the seafloor scatterering body

根据散射体在海底的分布与散射单元面积的关系， 以及考虑声呐分辨力的一般规律， 方位角分辨单元和距离分辨单元的划分均采用等间隔划分方法， 每个散射单元中的散射体数目服从泊松分布。

2.2散射元的散射强度

收发合置的声呐发出信号后， 一部分声波直接由海底界面散射入水中， 另一部分则进入海底沉积层， 在海底沉积层发生折射、散射， 重新射入水中， 因此， 散射不仅在海底界面上产生， 在进入沉积层后遇到散射体同样发生散射。GABIM（geoacoustic bottom interaction model）模型［7］是充分考虑了海底任意分层介质、沉积层界面的粗糙度以及介质的弹性效应等环境因素对海底散射的影响而建立的一种较为复杂的海底散射模型， 具有优化的散射强度计算方法， 并且可以适应多变的海洋环境。

由于海底的复杂环境对散射强度存在很大的影响， 为了计算出更为准确的散射强度和便于仿真实现， 在 GABIM模型的基础上， 根据海底介质特性的不同， 将海底分为常见的泥沙沉积层和由岩石构成的基层， 两层都是粗糙、各向同性的，并将其引入到混响的空时模型中， 然后充分考虑粗糙海底界面、沉积层与基层之间界面以及在沉积层中发生的体积散射等对散射回波的共同作用。其中， 海底环境参数主要包括： 海底界面粗糙度、沉积物类型、沉积物密度、沉积层衰减系数和谱强度等。

散射强度

式中： ξr（θ）表示海底沉积层和水之间界面粗糙度散射截面； ξvs（θ）和ξvb（θ）分别表示沉积层和基层的体积异质性对散射截面的贡献； ξbr（θ）表示基层粗糙度散射截面， 它们都是无量纲的量。

从计算过程中， 海底的散射强度与掠射角大小、发射信号的参数、海底环境因素有关， 即随着海底环境的变化来改变谱强度、谱指数等环境参数的取值， 其中， 谱强度的取值反映了海底的起伏粗糙程度， 仿真时的取值一般小于0.000 6，谱指数的常用取值范围为（2，4）， 从而所建立的散射模型具有良好的环境适应性。

2.3混响的时域模型

对于收发合置的声呐， 综合信号发射强度、散射单元散射强度、基阵指向性、传播扩散衰减、海水吸收性以及海底不同介质的影响， 可得阵元接收到的混响信号为

式中： Nr为距离分辨单元数， 距离单元被允许的最大时延间隔为Δτ， Δτ小于声呐系统的时延分辨率； L为方位角分辨单元数；代表收发基阵的指向性； A为散射单元的随机幅度，服从正态分布；是海底散射项；是界面散射的衰减函数， 其中1/r是球面距离扩展损失， r为散射单元与声呐的径向距离； α是吸收系数， 且α=0.036×f（3/2）；Np为每个分辨单元的散射体数， 散射体数服从泊松分布； x（ t）为发射信号； τn为双程传播时延；φ为散射过程中引起的随机相位扰动。

2.4阵列空时信号模型

图4为M个阵元空间位置上任意分布的基阵。

图4　任意分布基阵模型Fig. 4　Model of arbitrary array

基阵第m个阵元接收到的信号为

假设接收到的N个散射信号均为窄带信号，且中心频率均为f0， 对于较小的时延τm（θsn，φsn），可近似用其解析信号的1个相移来表示， 则M元任意分布基阵的输出信号用矩阵形式表示为

创新是引领发展的第一动力，是建设智慧城市的战略支撑。扬中市产业特色鲜明，智慧城市建设给扬中传统产业带来新机遇的同时也带来了新挑战。虽然扬中已经在加快主导产业与现代信息技术的融合，但不可否认的是扬中市传统产业的自主创新能力仍然较弱，部分产业项目建设进展较为缓慢，而新产业、新业态的成长需要更长时间，大项目、新项目的储备不足，导致城市发展后劲较弱。

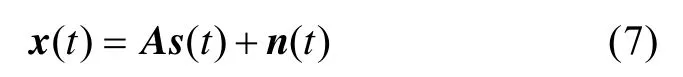
其中， M个阵元输出为

N个散射信号为

M个阵元上的加性噪声为

矩阵A称为阵列流形（array manifold）， 且

其中， a（θsn，φsn）称为基阵对第n个散射信号的响应向量， 且

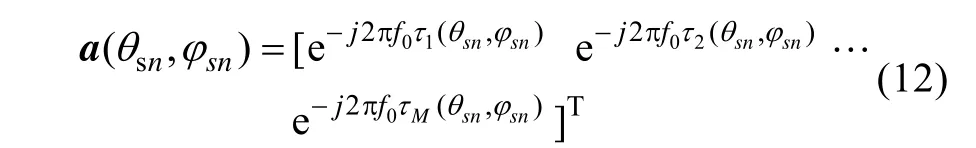
2.5混响空时2D谱

采用最小方差谱功率谱来分析混响2D分布空时特性。在混响矩阵确知的情况下， 估计空时2D混响的功率谱

式中： R-1为混响协方差矩阵的逆； S（θs， φs，fd）表示空时2D数据矢量， 是方位（θs， φs）和多普勒频移fd的函数， 且

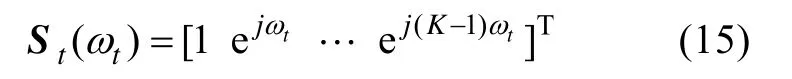
式中， ωt=2πfd/fs为归一化的时域角频率，

Ss（ωs）为空域导向矢量， 线列阵的空域导向矢量可表示为

式中， ωs=2πd sinθs/λ为归一化的空域角频率。

关于混响协方差矩阵的求取， 待检测数据的时域采样点数为K。设xmk（m=1，2，…，M， k= 1，2，…，K）表示第M个阵元第K次时域采样的数据， 则空时2D采样数据为X=［XT，…，XT］T，s，1s， K其中Xs，k=［X1k，…，XMk］T表示第k次空间快拍数据（k=1，2，…，K）。空时数据X就是所有K次快拍数据顺次排列形成。基阵的空时协方差矩阵为

3　仿真结果与分析

设一收发合置的均匀线列阵在距海底60 m处， 阵元个数M=8， 阵元间距为半波长， 海底散射体（N=1 000）在（150， 1 000） m的距离内均匀分布。平台沿x轴方向运动，航行速度20 kn。采用脉宽为 0.1 s的CW信号， 载频f0=20 kHz 。海底泥沙沉积层衰减系数为0.01， 谱强度为0.000 1，谱指数为3； 岩石基层衰减系数为0.02， 谱强度为0.006 5， 谱指数为3.25。

图5给出了海底混响的时域波形。

图5　混响时域波形图Fig. 5　Waveform of reverberation in time domain

由于基阵与散射体之间的相对运动引起了多普勒频移， 因此导致了混响信号的频谱相对于发射信号有了一定的带宽， 图6中从发射信号频域图和混响频域图的对比中可以看出， 混响的频谱展宽约为500 Hz。在不同的海洋环境下， 海洋环境参数发生明显变化时， 仿真得到的混响数据也不同。而且越是起伏粗糙的海底环境， 使得散射强度增大， 从而造成混响的强度变大。

从图7可以看出， 混响信号与发射信号的时间相关具有较好的一致性。

从图8和图9可以看出， 混响瞬时值近似服从高斯分布， 混响包络近似服从瑞利分布， 仿真结果同理论期望相符合。

图6　发射信号频域图与混响频域图Fig. 6　Waveform of transmitted signal and reverberation in frequency domain

图7　混响信号的自相关Fig. 7　Autocorrelation of reverberation signals

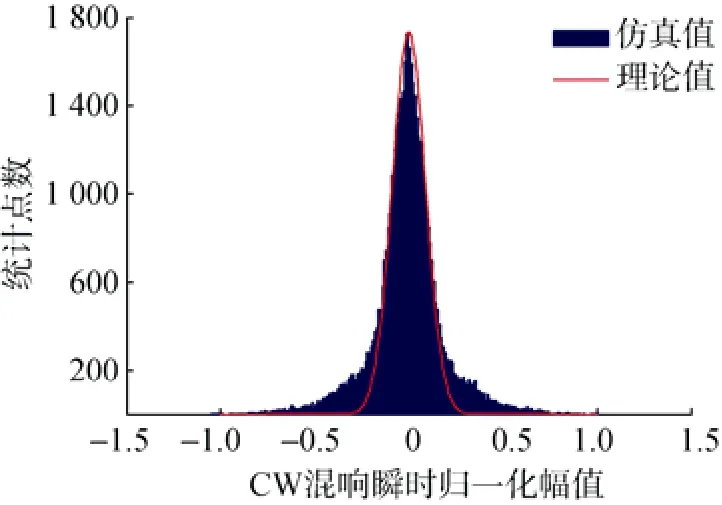
图8　仿真数据的瞬时值Fig. 8　Instantaneous value of simulation data

图9　仿真数据的包络值Fig. 9　Envelop value of simulation data

下面利用上述2.5节中的理论分析， 分别对前视阵和侧视阵的空时2D混响功率谱进行仿真，如图10～图11所示。

图10　前视阵混响功率谱Fig. 10 Power spectrum of reverberation for forward-looking array

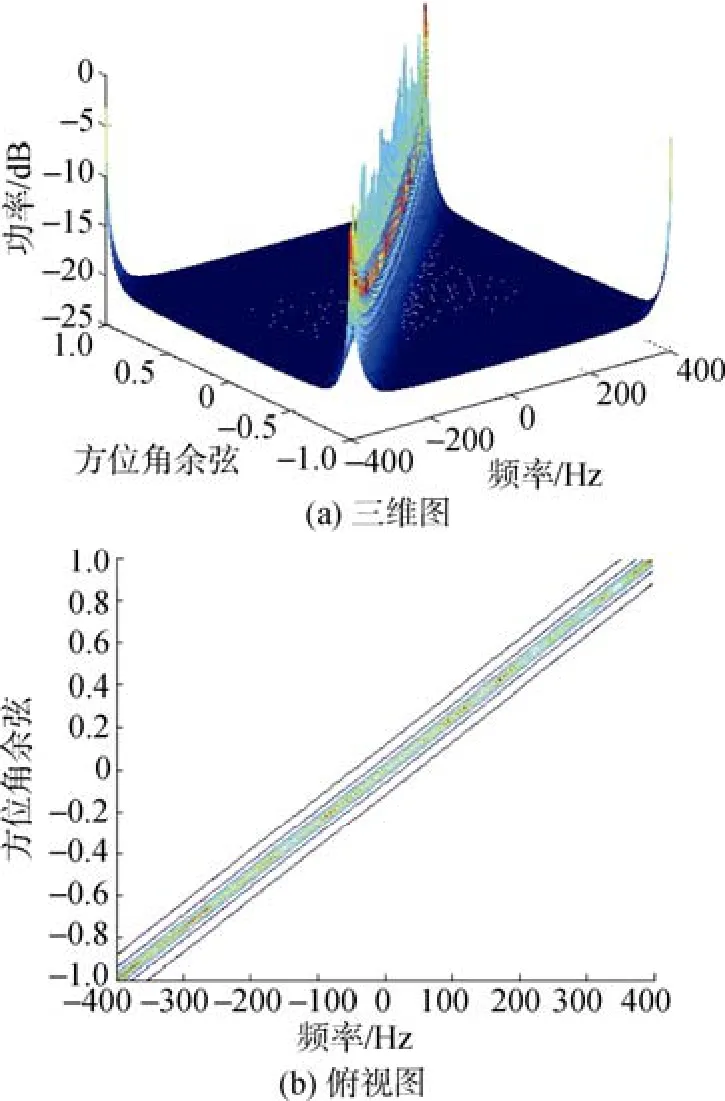
图11　侧视阵混响功率谱图Fig. 11　Power spectrum of reverberation for side-looking array

由仿真结果可知， 该仿真模型能够很好地反映海底混响频域扩展特性和海底混响的空时特性，符合混响多普勒频移和空间入射角的关系， 验证了文中空时混响模型的正确性。

4　结束语

为了使海底混响更加符合实际的海洋环境，充分考虑海底介质对混响的显著影响， 建立了可适用于任意阵型的分层海底环境下的混响空时模型， 在不同的海底介质、散射体的不同分布以及选取不同阵型等情况下， 可以适时调整模型参数来产生相应的混响信号， 通过对混响频谱、瞬时值分布、包络分布及其空时特性的仿真验证， 结果表明， 混响模型符合理论要求和实际的海底环境， 并且适应性强， 可有效地应用于混响信号的模拟和空时处理技术之中。

［1］ Luby J C， Lytle D W. Autoregressive Modeling of Nonstationary Multibeam Sonar Reverberation［J］. IEEE Journal of Oceanic Engineering， 1983， 12（1）： 116-129.

［2］ 璟苏绍， 郭熙业， 王跃科. 一种海底混响时间序列仿真方法研究［J］. 系统仿真学报， 2010， 88（8）： 1853-1861.

Su Shao-jing， Guo Xi-ye， Wang Yue-ke. A Bottom Reverberation Time Sequence Simulation Method Research［J］. Journal of System Simulation， 2010， 88（8）： 1853-1861.

［3］ 赵烨， 冯西安， 郑玉峰， 等. 海底混响的空时模型及仿真［J］. 计算机仿真. 2011， 28（12）： 398-401.

Zhao Ye， Feng Xi-an， Zheng Yu-feng， et al. Seafloor Reverberation Space-time Model and Simulation［J］. Computer Simulation， 2011， 28（12）： 398-401.

［4］ Stanley G C， John C G．A Model for Numerical Simulation of Nonstationary Sonar Reverberation Using Linear Spectral Prediction［J］. IEEE Journal of Oceanic ngineering， 1983， OE-8（1）： 21-36.

［5］ 耿云辉， 冯西安. 一种基于K-分布模型及多次途径的浅海混响仿真方法［J］. 鱼雷技术， 2013， 21（3）： 179-183.

Geng Yun-hui， Feng Xi-an. A Simulation Method of Shallow Water Reverberation Based on K-distribution Model and Multipath［J］. Torpedo Technology， 2013， 21（3）： 179-183.

［6］ 房媛媛， 李亚安， 崔琳. 基于运动平台的海底混响建模与仿真［J］. 声学技术， 2013， 32（6）： 473-476.

Fang Yuan-yuan， Li Ya-an， Cui Lin. Modeling and Simulation of Sea Bottom Reverberation Based on Moving Platform［J］. Technical Acoustics. 2013， 32（6）： 473-476.

［7］ Jackson D R， Odom R I， Boyd M L， et al. A Geoacoustic Bottom Interaction Model（GABIM）［J］. IEEE Journal of Oceanic Engineering， 2010， 35（3）： 603-617.

（责任编辑： 杨力军）

Modeling and Simulation of Layered Seafloor Reverberation Space-Time for Arbitrary Array

ZHAO Dong-liang，LIANG Hong，YANG Chang-sheng，ZHENG Ya-ning
（School of Marine Science and Technology， Northwestern Polytechnical University， Xi′an 710072， China）

Considering the layered medium in the seafloor environment， a reverberation space-time model adapted to the arbitrary array was established for the layered seafloor. The impacts of the Doppler shift， the direction of scattering body，the inhomogeneity of sediment and basement， and the sediment-water interface on the reverberation were considered in the model. All the received scattering signals were superposed at the array element to form the single channel output of the reverberation. The proposed space-time model of the reverberation was adapted to the complex seafloor environment. The reverberation of continuous wave（CW） signal was simulated using this model. By comparing the characteristics of the simulated reverberations in time domain and 2D space-time domain with the theoretical expectation， the validity and accuracy of the proposed reverberation space-time model are proved.

seafloor reverberation； arbitrary array； layered seafloor； space-time model

TJ630.34

A

1673-1948（2015）06-0414-06

10.11993/j.issn.1673-1948.2015.06.004

2015-04-12；

2015-10-29.

国家自然科学基金（61379007）

赵栋良（1991-）， 男， 在读硕士， 研究方向为水下信号与信息处理.