环形气囊水下充气展开过程仿真与分析
叶慧娟,王昕晔, 张 宁
(1. 海军工程大学 兵器工程系, 湖北 武汉, 430033; 2. 海军工程大学 科研部, 湖北 武汉, 430033)
环形气囊水下充气展开过程仿真与分析
叶慧娟1,王昕晔2, 张宁1
(1. 海军工程大学 兵器工程系, 湖北 武汉, 430033; 2. 海军工程大学 科研部, 湖北 武汉, 430033)
为了对水下航行器环形气囊的水下充气过程进行研究, 依据控制体积方法基本思想, 运用热力学和弹性体弹性本构模型等理论, 建立了气囊水下充气过程数学模型, 并在此基础上编制计算程序, 对该气囊水下充气过程进行了仿真, 同时对影响气囊水下快速充气的因素进行分析。仿真结果表明, 所建立的模型能基本反映环形气囊水下充气过程相关参数的变化规律, 可为后续水下航行器上浮过程的仿真研究提供参考。
水下航行器; 环形气囊; 弹性体
0 引言
气囊在各个行业中的应用比较广泛, 例如汽车安全气囊[1]、航天器着陆缓冲气囊等[2]。此外,其在特殊领域业中也发挥着重要作用, 如船舶水下气囊等[3]。文中所介绍的环形气囊主要应用在水下航行器(如鱼雷操雷或无动力运载器)上[4],环形气囊布置在水下航行器头部, 其功用是, 当水下航行器需要上浮时, 其内部气瓶充气阀打开给气囊充气以产生浮力, 从而将水下航行器带到水面。
以往气囊的充气展开仿真方法多采用控制体积(control volume, CV)法和任意拉格朗日-欧拉(arbitrary Lagrange-Eulerian, ALE)法[2], 适用于计算气囊充气展开过程中结构的变形, 其目的是为气囊结构设计服务, 这些方法结果精度高, 但计算建模复杂, 计算量大, 对硬件要求高且计算时间长, 不大适合于水下航行器上浮运动仿真研究。为此, 文章将依据CV法的基本思想, 运用热力学和弹性体的弹性本构模型等理论, 建立了水下航行器环形气囊水下充气展开过程的1D数学模型, 进行了气囊水下充气过程的仿真, 并分析了影响气囊水下充气膨胀的因素, 以获得气囊容积随时间的变化规律以及影响其容积变化的主要因素, 从而为进一步研究水下航行器上浮过程提供参考。
1 气囊充气过程建模基本假设
水下航行器环形气囊的实际水下充气展开过程十分复杂。考虑到实际充气过程经历时间极短,为便于问题研究, 做如下假设: 1) 不考虑气囊折叠部分展开时间(该过程时间极短); 2) 气体从气瓶流经充气阀给气囊充气是一个绝热膨胀的节流过程, 忽略气囊内空气通过气囊与海水的热交换损失; 3) 气囊内部气压均匀, 其外部所受的海水压强均为气囊环形中心处的海水压强。
2 气囊充气过程数学建模
2.1气囊内气体状态方程
将气囊内部视为控制体, 根据以上假设, 可用热力学第一定律描述该控制体内的过程: 气囊内气体的内能等于气囊内原始气体的内能加上通过充气阀注入气囊的气体热焓之累积值, 减去气囊膨胀克服海水压强所做的功, 再减去克服气囊弹力所做的功。根据以上的描述, 气囊水下充气过程的能量平衡方程可表示为
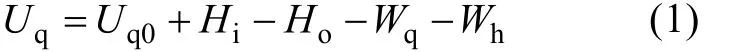
式中: Uq为气囊控制体内气体的内能; Uq0为气囊控制体(未展开前)原有气体的内能; Hi为通过充气阀注入气囊的焓; Ho为充气过程中泄漏的焓(若无泄漏则Ho=0); Wq为气囊内气体克服气囊弹力所做的功; Wh为气囊膨胀克服海水所做的功。
根据能量守恒方程以及气体热力学定理, 经推导得到气囊内气体状态方程为
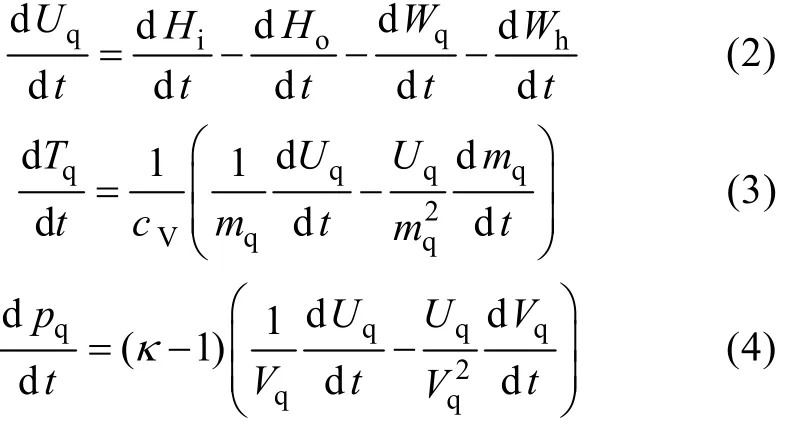
式中: Tq为气囊内气体温度; pq为气囊内气体压强; mq为控制体内气体质量; cV为空气的定容比热; κ为空气比热比(绝热指数); 。
其中, 由气瓶注入气囊的热焓注入率可按下式计算

式中: mB为气瓶中气体的瞬时质量; TB为气瓶中气体的热力学温度; cp为空气的定压比热。
2.2气囊充气流量方程
设通过充气阀流入气囊的气体质量流量为
气体的瞬时质量变化率为

流经充气阀的气体质量流量可按下式计算
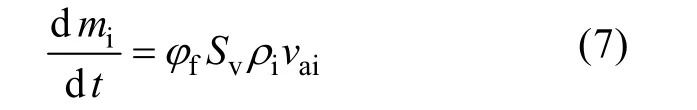
式中: φf为充气阀的空气流量系数; Sv为充气阀流通面积, Sv=πdv2/4, 其中, dv为充气阀通径; ρi为充气阀特形孔处气流的密度; vai为气流通过充气阀的流速。

式中: pB为气瓶的瞬时压强; pi和Ti分别为充气阀通孔处的气体压强与温度; R为空气的气体常数。
2.3气囊容积变化率模型
以环形气囊微元为研究对象(见图1), 假设忽略其弯曲应力, 则有微元力平衡方程为


图1 气囊受力示意图Fig. 1 Schematic of the forces acting on a bladder
式中: pq为气囊内部气体压强; pH为气囊外部海水压强, 其中:hρ为海水密度, H为海水深度, p0为大气压; r为环形气囊圆形切面内径; τ为环形气囊厚度; σ为气囊弹性材料因膨胀产生的拉伸应力。
将气囊膨胀过程中微元所受应力视为单轴拉伸微元所产生应力, 则依据弹性材料的弹性本构模型中的高斯定理[5], 则有

式中: λ为弹性材料的伸长率; CR为橡胶初始剪切弹性模量。
当微元的伸长率为λ时, 由于弹性体在膨胀过程中体积保持不变, 因此有

其中: r0和0τ分别为气囊充气前圆形切面内径与厚度。将上式代入式(12), 有
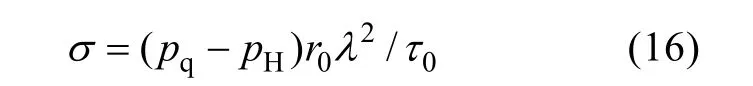
联立式(13)和式(15)进行求导, 经整理后有

环形气囊容积的计算模型为
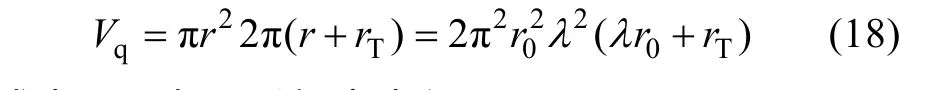
式中: rT为环形气囊内径(见图1)。
则其容积变化率为
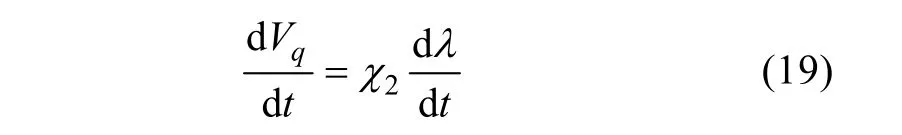
2.4气囊克服海水压强做功的功率方程
由气囊容积变化率有气囊克服海水压强做功的功率方程为

2.5克服气囊弹力做功的功率方程
当气囊弹性材料微元的伸长率为λ时, 经推导有气囊内气体克服气囊弹力所做的功为

对式(20)求导有其功率方程
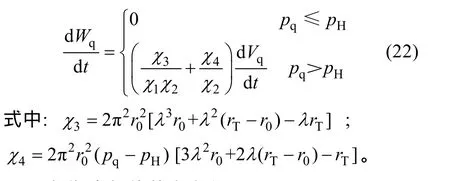
2.6气瓶内气体状态方程
假设充气过程为理想气体绝热过程, 则气瓶内气体状态模型为
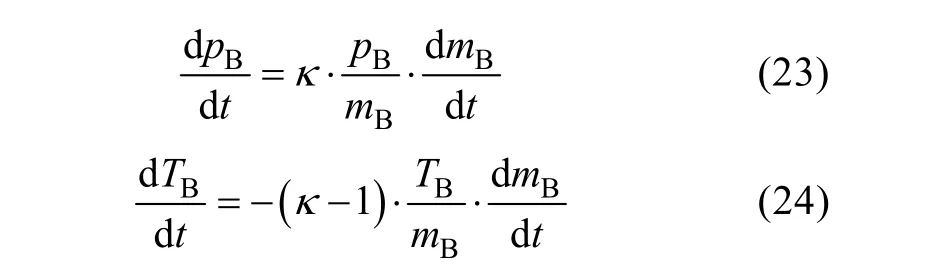
3 气囊水下充气过程仿真与分析
根据以上建立的数学模型, 以4阶龙格-库塔算法作为求解微分方程的基本算法编制仿真程序。在给定初始条件下, 运用仿真程序即可对气囊水下充气过程进行仿真。
3.1仿真主要参数
气瓶初压pB0=10 MPa; 气瓶气体初温TB0=288.0 K; 气瓶初始容积VB0=10 L; 气囊初始厚度τ0=0.01 m; 气囊橡胶材料的初始剪切弹性模量CR=0.5 MPa; 充气阀通径dv=0.01 m; 海水深度H=50 m; 海水密度ρh=1 025.0 kg/m3; 环形气囊内径rT=0.5 m。
考虑到实际情况中, 气囊的容积增长是有限度的。通过对文献[6]中气象气球充气前后容积情况进行分析可知, 气象气球的橡胶材料最大伸展率为5~7, 因此, 在仿真中以充气阀打开为计时开始点, 以气囊达到最大充气容积(即橡胶材料伸展率等于5)时为结束点, 整个仿真时间即气囊充气时间。
3.2仿真结果与分析
在以上仿真条件下的仿真结果如图2~图5所示。
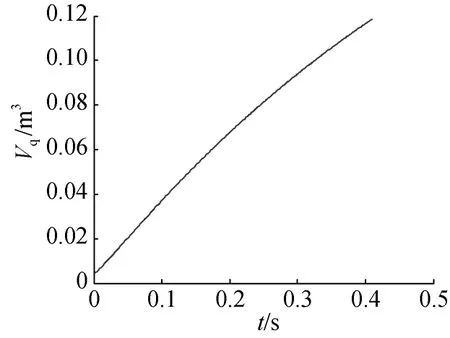
图2 气囊容积随时间变化图Fig. 2 Curve of the bladder volume versus time
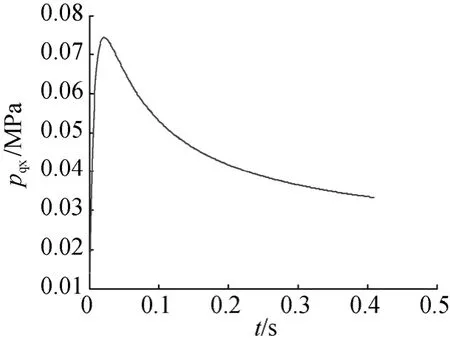
图3 气囊内气体相对压强随时间变化图Fig. 3 Curve of the relative air pressure in bladder versus time

图4 气囊内气体质量随时间变化图Fig. 4 Curve of the air mass in bladder versus time
下面给出海水深度、气瓶初始压强、充气阀通径单个因素变化时的仿真结果。
1) 不同海水深度条件下的仿真结果如图6~图8所示。
2) 不同气瓶初始压强条件下的仿真结果如图9~图11所示。

图5 气瓶内压强随时间变化图Fig. 5 Curve of the air pressure in bottle versus time

图6 不同海水深度条件下气囊容积曲线Fig. 6 Curves of the bladder volume versus time under different depth below sea level

图7 不同海水深度条件下气囊内气体相对压强曲线Fig. 7 Curves of the relative air pressure in bladder versus time under different depth below sea level

图8 不同海水深度下气囊内气体质量曲线Fig. 8 Curves of the air mass in bladder versus time under different depth below sea level
3) 不同充气阀通径条件下的仿真结果如图12~图14所示。

图9 不同气瓶初始压强条件下气囊容积曲线Fig. 9 Curves of the bladder volume versus time under different initial pressure in bottle

图10 不同气瓶初始压强条件下气囊内气体相对压强曲线Fig. 10 Curves of the relative air pressure in bladder versus time under different initial pressure in bottle
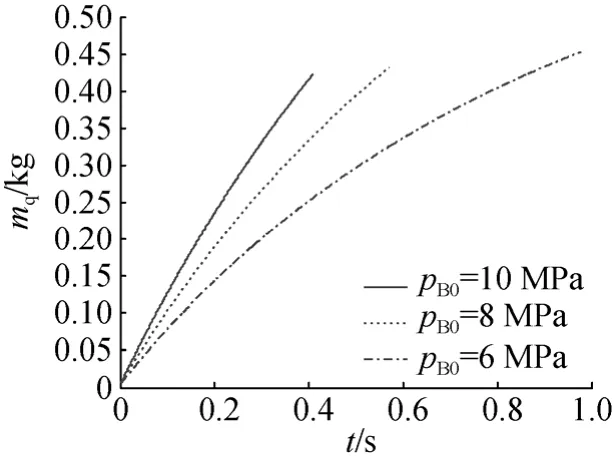
图11 不同气瓶初始压强条件下气囊内气体质量曲线Fig. 11 Curves of the air mass in bladder versus time under different initial pressure in bottle

图12 不同充气阀通径条件下气囊容积曲线Fig. 12 Curves of the bladder volume versus time under different diameter of gas charging valve

图13 不同充气阀通径条件下气囊内气体相对压强曲线Fig. 13 Curves of the relative air pressure in bladder versus time under different diameter of gas charging valve

图14 不同充气阀通径条件下气囊内气体质量曲线Fig. 14 Curves of the air mass in bladder versus time under different diameter of gas charging valve
通过对仿真结果进行分析, 可以看出:
1) 在3.1节给定条件下, 气囊在0.41 s内完成气囊充气, 其充气展开后的容积为0.12 m3(见图2)。在充气过程中, 气囊内部的相对气体压强在充气开始时有压强峰值(接近0.074 MPa, 见图3), 这主要是因为充气开始时, 气囊初始容积较小, 气囊容积增长滞后造成的。在充气后期, 气囊内部的相对气体压强逐渐趋于平稳(约为0.033 MPa)。
2) 气囊充气时间与展开后容积受海水深度影响较大。在10 m, 30 m和50 m深度进行气囊充气时, 达到给定容积对应的充气时间分别为0.21 s, 0.3 s和0.41 s(见图6)。可见随着深度的增加, 气瓶内空气能量中用于克服海水压力做功的部分增大, 相应的用于克服气囊弹力做功的部分减少, 导致气囊容积增长率减小, 充气时间增大。气囊充气展开后的内部气体相对压强随深度变化很小(见图7), 气囊内总充气质量随深度增加而增加(见图8)。
3) 气瓶初始压强主要影响气囊水下充气的容积增长率与充气时间。在气瓶容积给定时, 气瓶初始压强体现为气瓶内压缩空气对气囊充气时的做功能力。当气瓶初始压强由10 MPa减少到6 MPa时, 气囊充气时间由0.41 s增加到0.97 s(减少约0.56 s, 见图9), 充气质量变化率与气瓶初始压强成正比(见图11), 而气囊充气展开后的内部气体相对压强与总充气质量变化不大(见图10和图11)。
4) 充气阀通径变化直接影响充气时进入气囊的气体质量流量, 进而影响气囊充气展开时间。充气阀通径增加, 气囊水下充气的容积增大,气囊充气时间变短(见图12)。充气阀通径对气囊内部总充气质量以及气囊内部相对气体压强等影响不大(见图12~图14)。
4 结论
在所建立的数学模型基础上, 对环形气囊水下充气过程进行了仿真, 仿真结果表明, 所建立的数学模型能基本描述环形气囊水下充气过程。仿真中还对充气时不同的海水深度、气瓶初始充气压强以及充气阀的通径对环形气囊水下充气过程的影响进行了定量分析得到以下结论:
1) 气囊充气时所处的海水深度增大, 气囊克服海水压力做功相应增大, 导致气囊容积增长率减小, 充气时间增加;
2) 气瓶初始充气压强直接体现为对气囊的做功能力, 该压强与气囊容积增长率成正比;
3) 充气阀的通径影响气囊充气的效率, 因而对充气时间影响显著, 两者成反比关系。这些变参数的仿真也进一步表明所建立的数学模型能反映气囊充气过程的基本变化规律, 该模型有待后续试验对比验证再进一步完善后, 可用于水下航行器上浮过程的仿真研究中。
[1]钟志华, 杨济匡. 汽车安全气囊技术及其应用[J]. 中国机械工程, 2002, 11(Z1): 234-238.
Zhong Zhi-hua, Yang Ji-kuang. Automotive Airbag Technology and Its Application[J]. China Mechanical Engineering, 2002, 11(Z1): 234-238.
[2]温金鹏, 李斌, 杨智春. 缓冲气囊冲击减缓研究进展[J].宇航学报, 2010, 31(11): 2438-2447.
Wen Jin-peng, Li Bin, Yang Zhi-chun. Progress of Study on Impact Attenuation Capability of Airbag Cushion System[J]. Journal of Astronautics, 2010, 31(11): 2438- 2447.
[3]孙菊香. 船舶气囊下水技术综述[J]. 中国修船, 2010,23(6): 42-46.
Sun Ju-xiang. Something on Technique for Ship′s Going Into Water by Air Bag[J]. China Shiprepair, 2010, 23(6):42-46.
[4]王栋, 金先龙, 曹源, 等. 波浪作用下浮囊式操雷海面漂浮数值模拟[J]. 系统仿真学报, 2013, 25(5): 894-898.
Wang Dong, Jin Xian-long, Cao Yuan, et al. Numerical Simulation of Floating Airbag-type Experimental Torpedo Under Wave[J]. Journal of System Simulation, 2013,25(5): 894-898.
[5]罗文波, 谭江华. 橡胶弹性材料的一种混合本构模型[J]. 固体力学学报, 2008, 29(3): 277-281.
Luo Wen-bo, Tan Jiang-hua. A Hybrid Hyperelastic Constitutive Model of Rubber Materials[J]. Chinese Journal of Solid Mechanics, 2008, 29(3): 277-281.
[6]肖迪娥, 张望. 气象气球的现状与发展(一)[J].中国橡胶,2009, 25(9): 11-14.
Xiao Di-er, Zhang Wang. The Current Situation and Development of Meteorologic Balloon (1) [J]. China Rubber,2009, 25(9): 11-14.
(责任编辑: 陈曦)
Simulation on Underwater Inflation Process of Annular Bladder
YE Hui-juan1,WANG Xin-ye2,ZHANG Ning1
(1. Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China; 2. The Scientific Research Department, Naval University of Engineering, Wuhan 430033, China)
To reveal the underwater inflation process of an underwater vehicle′s annular bladder, mathematical models of the underwater inflation process are built based on the theories of thermodynamics and the elastic constitutive model of elastic body. Simulation is conducted to analyze the factors influencing the bladder′s underwater inflation process. The result shows that the present mathematical models can be used to analyze the change rules of the related parameters during underwater inflation process of an annular bladder, and to simulate floating process of an underwater vehicle.
underwater vehicle; annular bladder; elastic body
TJ630
A
1673-1948(2015)03-0166-06
2014-12-03;
2015-01-08.
叶慧娟(1974-), 硕士, 副研究员, 硕士生导师, 主要研究方向为武器系统仿真与试验.

