用于运动声源定位的解多普勒算法

姜成坤，白建斌，陈志菲

（1. 中国船舶重工集团公司 第705研究所， 陕西 西安， 710075； 2. 陕西师范大学 物理学与信息技术学院，陕西 西安， 710119）

用于运动声源定位的解多普勒算法

姜成坤1，白建斌1，陈志菲2

（1. 中国船舶重工集团公司 第705研究所， 陕西 西安， 710075； 2. 陕西师范大学 物理学与信息技术学院，陕西 西安， 710119）

针对获取运动目标各部位噪声源的位置信息意义重大, 但其辐射噪声存在多普勒效应的问题。介绍了面向阵列接收信号的基于非线性插值运算的解多普勒算法, 包括单通道单聚焦点型, 单通道多聚焦点型和多通道多聚焦点型, 以补偿辐射噪声的多普勒频移和幅度衰减, 从而提高运动目标噪声源识别定位的准确度。外场试验中解多普勒前后的试验结果表明, 该算法能有效消除多普勒效应带来的影响, 提高了噪声源定位的精度。

多普勒效应； 噪声源定位； 非线性插值

0　引言

多普勒效应是1842年由奥地利物理学家多普勒首先在声学上发现的， 主要是指当波源和接收器之间有相对运动时， 接收到的频率与波源的实际频率出现差别的现象。如今， 多普勒效应已广泛应用于医学诊断、气象探测、卫星定位等多个领域［1］。但对于向外辐射声波的运动目标而言，要想获得真实的辐射信号， 还需要对接收信号通过解多普勒运算进行频率和幅度补偿。

近年来， 国内学者对该领域进行了较为深入地研究。周晓华利用小波变换法消除了运动声源的多普勒效应［2］， 但方法较为复杂； 徐初杰介绍了对水下运动目标进行多普勒测向的方法， 但仅适用于波源做匀速圆周运动的情况［3］； 刘方提出的多普勒声音信号时域插值拟合校正方法则对采样初始时刻的要求特别严格［4］； 李兵针对短时多普勒效应提出的短时运动波叠加分析法则没有进行幅度补偿［5］。

文中针对阵列接收信号提出了适用于任意航迹基于非线性插值的解多普勒算法， 并通过合理选择解多普勒后各阵元数据的起始时间点， 保持了各阵元间信号的时延差异关系， 有利于后续的噪声源识别处理。该算法简单易懂， 能够同时对频率和幅度进行处理和补偿， 不需要预知噪声源的频率特征。

1　用于运动声源定位的解多普勒算法

1.1多普勒的影响

经典阵列信号处理方法基本都是针对静止声源， 因此需要根据运动声源的航迹对接收信号解多普勒， 去除多普勒效应造成的频移和幅度增益后再进行噪声源定位。解多普勒前后的信号分别属于运动和静止声源辐射信号， 图1给出了近场点声源的信号辐射模型［6］。

图1　近场点声源辐射模型Fig. 1　Radiation model of point source in near field

图中， 点声源D作直线运动， 静止的阵元S1，S2等采集其辐射的信号， 并假定声源D辐射波形为xe（te）， 阵列接收到的信号为xr（tr）， 其中te和tr分别为辐射端和接收端的时间轴， 则xr（tr）可表示为

式中， c为声速。式（1）表示各阵元在tr时刻接收的信号是D点在te时刻下辐射的经幅度衰减后的信号， 声源运动时r（te）随时间变化， 导致接收端信号的瞬时频率和幅度都在变化。

图2给出了静止和运动情形下信号波形变化的示意图。图2（a）中声源D保持静止， 因此接收端波形xr与辐射端信号xe相比， 仅存在固定的幅度衰减和初相位的变化， 信号频率保持不变。采用经典阵列信号处理方法对近场目标定位时， 可截取［tra， trb］时间段内各阵元接收信号后， 根据空间搜索点的位置补偿幅度衰减和相位差后即可得到空间谱， 从而定位噪声源。

图2　静止和运动声源接收信号示意图Fig. 2　Schematic of received signal from static and moving sound sources

图2（b）中声源D运动时， 有如下特点。

1） 接收端信号xr与辐射端波形xe相比， 由于辐射端te时间轴上的时间间隔Δt， 对应到接收端tr时间轴上会不断变化， 即拉伸或压缩波形使接收端信号存在时变多普勒频移。

2） 声源D与阵元S间距离r（te）不断变化， 使得波形的幅度衰减量也随时间变化。

3） 若截取［tra， trb］时间段内各阵元接收信号，各阵元初相位差异也与静止声源的初相位差异不同， 因此无法直接采用经典阵列信号处理方法来定位噪声源。

1.2辐射和接收端时间轴关系

为了将接收信号解多普勒为静止情形下的声辐射， 可进行式（1）的逆过程

即根据航迹将接收信号对应到辐射时刻， 并补偿传播衰减。式（2）的核心在于tr和te间的对应关系， 这需要根据航迹和阵元间的几何关系来推导。

如图3所示， 假设已知空间中某直线航迹上若干点的坐标及其辐射时刻， 并且阵元S的坐标已知。对于给定的接收时刻tr， 若其对应的辐射时刻为te， 并且此时声源位于D点， 则有

图3　3D空间中航迹示意图Fig. 3　Schematic of the track in three-dimensional space

另外， 若与D点相邻的2个航迹上的已知点为A和B， 其辐射时刻为tga和tgb， 则AB段的矢量速度可表示为这样D的坐标为， 从而DS可表示为

式（5）和式（6）等价， 它们分别是te和tr的一元二次方程， 给定其一即可求解另一个。

上述推导中假定AB段目标作匀速直线运动，实际中AB两点的时间间隔较小， 故式（5）和式（6）成立。理想情况下， 若目标作匀速直线运动， 则可任意选取航迹上2点作为AB点。

1.3聚焦点的坐标转换

图3中假设聚焦点为D， 即将接收信号解多普勒为D点辐射的静止声信号， D点在航迹时间轴tg下的空间坐标D=［A； B； …］是已知的。若运动目标不是1个点声源， 而是假定为1个线性尺寸物体， 就会存在多个聚焦点。对于聚焦点， 则需要根据Di和D之间的几何关系来将tr换算为te。

如图4所示， 某参考源位于运动目标上的D点， 其航迹［tg， D］已知。对于运动目标上某个聚焦点Di≠D， 需要估计其航迹［tg， Di］， 才能利用式（5）和式（6）来计算tr和te。

图4　聚焦点的坐标转换Fig. 4　The coordinates transition at focus point

另一方面， 为了便于解多普勒时划分网格点，通常要在运动目标上建立以参考源D为原点的本地坐标系px-py-pz， 这样求解本地坐标Di的航迹［tg， Di］就需要进行坐标系转换。px-py-pz坐标系中假定运动目标航向方向为x轴正向， x和px轴近似同向时， py轴也和y轴近似同向， 否则方向相反， pz轴总是指向上方。这里主要关心px轴方向的噪声源， 即在px轴上划分网格点。这样针对py和pz轴旋转平移即可实现坐标变换， 即

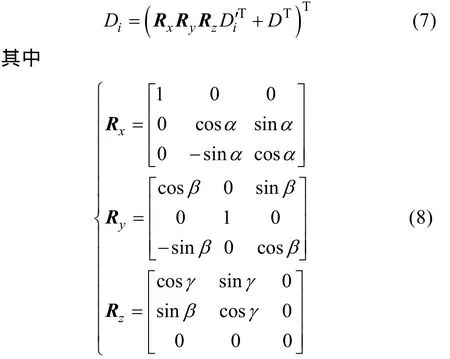
式中， α， β和γ分别是绕px， py和pz轴旋转的角度。由于pz轴总是垂直向上， α和β取值范围为［-π/2， π/2］， γ的取值范围则为［0， 2π］。通过式（7）就可以将D点的航迹［tg， D］换算成Di点的航迹［tg，Di］， 进而利用式（5）和式（6）换算tr和te。

1.4插值解多普勒

1.4.1单通道单聚焦点

设定本地坐标系下的聚焦点Di的航迹为［tg，Di］， 所截取的［tra， trb］时段内的接收信号的时间轴tr是等间隔时间序列， 根据式（5）可得到其对应的［tea， teb］时段内的非等间隔辐射时间序列， 这样补偿传播损失后得到的解多普勒后信号是非等间隔采样信号， 不利于后续处理。为此， 需要构建［tea， teb］时间段内的等间隔辐射时间序列te=（tea：1/frs：teb）， 其中frs为重采样频率， 即解多普勒后信号的采样频率， 通常它小于接收信号采样频率fs。然后根据式（6）得到其对应的接收时刻tr＇， tr＇即为非线性的插值拟合时间序列， 再依照最小二乘算法拟合出以（tr， xr（tr））为插值点的插值函数， 非线性插值序列在插值函数中所对应的值即为补偿传播损失后即为xe（te）。为了模拟静止声源辐射得到的接收信号， 还需添加固定的传播损失， 即

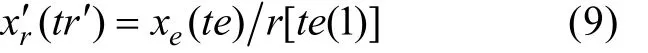
1.4.2多通道单聚焦点

对于给定的聚焦点Di， 不同阵元通道的共同截取时刻［tra， trb］对应的辐射起止时刻为［teaj，tebj］， j=1，…， M， 且M为阵元数。显然各个辐射时段的时长是不一样的， 为便于后续阵列信号处理，各通道应截取相同时长的辐射时段的信号， 即

各通道起始时刻仍取teaj， 以保持各通道的相位差异， 然后构造出各通道的辐射时间序列，通过非线性插值和传播损失补偿后得到辐射信号，最后由式（9）得到阵元接收的Di点辐射的静止声源信号， 具体步骤与单通道单聚焦点相同。

1.4.3多通道多聚焦点

实际噪声源识别时， 强线谱声源所在的聚焦点位置是未知的， 因此需要通过在运动目标上划分聚焦点， 分别针对每个聚焦点作噪声源识别。这与针对静止声源的空间谱搜索过程相似， 故运动声源噪声识别时需要在每个聚焦点上对阵列接收信号解多普勒， 分别估计每个聚焦点上的声辐射能量以确定强线谱声源的部位。

由多通道单聚焦点部分的介绍可知， 每个聚焦点下阵列解多普勒后信号的时间长度为，i=1，…，N， 其中N为聚焦点数， 它们存在一定差异。这不利于比较各聚焦点下的声源辐射能量，故要对各聚焦点采取相同的时间长度。实际处理中可根据截取的阵列接收信号时段［tra， trb］， 分别计算各聚焦点的时长Tei， 取其最小值作为最终采用的辐射时间长度， 即

余下的解多普勒步骤与单通道单聚焦点所述的过程相同。按照上述步骤解多普勒后的阵列接收信号和图2（a）中静止声源的接收信号相似， 后面可利用其计算采样协方差矩阵来估计噪声源的参数［7］。

2　试验验证

如图5所示， 试验中电瓶车携带2个扬声器作直线运动， 2个扬声器辐射单频信号的频率分别为600 Hz和1 200 Hz。航迹上放置6个间距4 m的加装加速度传感器的丁字尺， 用于记录真实航迹， 目标运动速度在4.47 m/s左右。信号接收端采用29元2.02 m长的线列阵， 线列阵与航迹间距45.6 m， 采集运动声源辐射信号解多普勒后进行声源定位。

图6给出了接收端和辐射端的部分仪器。采集系统连接29个传声器通道， 另有2个通道采集6个加速度传感器信号。在信号发射端， 试验中使用的是2个惠威D8.8+扬声器（A和B）。

根据航迹估计结果对接收信号解多普勒后即可对噪声源定位。由图7可知， 运动声源发出的信号被固定传声器接收后， 信号的幅值出现了尖峰， 即幅度发生了变化。

图5　试验示意图Fig. 5　Schematic of the experiment

图6　试验仪器Fig. 6　Experimental apparatus

图7　传声器接收信号的时域图Fig. 7　Time-domain curve of the signal received by microphone

由图8可知， 其频谱以 600 Hz 和1 200 Hz为中心向两边扩展， 产生了频移现象。由图9和图10可看出， 多普勒效应消除后信号的幅度没有了峰值， 基本保持平稳， 信号频率聚焦性也明显改善， 基本集中在中心频率处。

图8　传声器接收信号的频域图Fig. 8　Frequency-domain curve of the signal received by microphone

图9　解多普勒后信号时域图Fig. 9　Time-domain curve of the signal after eliminating Doppler effect

图10　解多普勒后信号频域图Fig. 10　Frequency-domain curve of the signal after eliminating Doppler effect

解多普勒后就可以用波束形成类算法进行噪声源定位。声源A和B在电瓶车本地坐标系上的坐标为［0.34，-0.32］m， 两者间距AB=0.66 m。下面给出不进行解多普勒运算直接用波束形成类算法对声源A和B的定位结果。参见图11。

图11　解多普勒前定位结果Fig. 11　Position result before eliminating Doppler effect

可以看出， 不解多普勒直接进行声源定位时误差很大， 但按照文中提到的方法进行解多普勒运算后， 声源的定位结果得到明显改善， 已经能够清晰的分辨2个声源。参见图12。

图12　解多普勒后定位结果Fig. 12　Position result after eliminating Doppler effect

正横距离为45.6 m时， 对噪声源B的定位误差在0.04 m左右， 对噪声源A的定位误差略大，在0.32 m左右， 这就直接增大了对两声源间距的定位误差。究其原因， 主要是因为A声源的频率较低， 太阳暴晒对扬声器低频辐射性能有较大影响， 而且阵列孔径太小也会使中低频声源的定位性能有所下降。表1是解多普勒前后准确定位值比较。

表1　具体定位结果比较Table 1　Comparison of position results

6　结束语

文中介绍的基于非线性插值的解多普勒算法，不需要预知噪声源的频率特征， 能够处理多频信号， 对频率和幅度同时进行补偿， 能有效应用于运动目标的噪声源识别中。但目前该算法只在针对强线谱噪声源进行解多普勒运算时精度较高，而且该算法需要预知运动声源的航迹信息， 这在后续工作中还需不断改进。

［1］刘广生， 李慧. 多普勒效应及其应用［J］. 南阳师范学院学报， 2006， 5（6）： 38-44.

［2］周晓华. 运动噪声源识别技术的研究［M］. 长春： 吉林大学出版社， 2008.

［3］徐初杰. 基于多普勒效应的水下目标定位技术研究［M］.广州： 华南理工大学出版社， 2013.

［4］刘方， 何清波， 沈长青， 等. 运动声源多普勒畸变信号的一种时域校正方法［J］. 声学学报， 2014， 39（2）： 185-190.

Liu Fang， He Qing-bo， Shen Chang-qing， et al. A Time Domain Correction Method for Doppler-distortion Signal form Acoustic Moving Source［J］. Acta Acustica， 2014，39（2）： 185-190.

［5］李兵. 运动汽车声场可视化方法研究［M］. 北京： 清华大学出版社， 2010.

［6］王静， 黄建国， 管静， 等. 运动点声源声传播模型的数值算法［J］. 云南大学学报（自然科学版）， 2003， 25（6）：503-506.

［7］Michel U. History of Acoustic Beamforming［M］. 1th ed. Berlin： Berlin Beamforming Conference， 2006.

（责任编辑： 杨力军）

Doppler Elimination Algorithm for Moving Sound Source Position

JIANG Cheng-kun1，BAI Jian-bin1，CHEN Zhi-fei2
（1. T1. The 705 Research Institute， Shipbuilding Industry Corporation， Xi′an 710075， China； 2.Institute of Physics and Information Technology， Shaanxi Normal University， Xi′an 710119， China）

It is of great significance to obtain the position information of the noise source of a moving target， but Doppler effect often exists in the radiated noise. This paper proposes nonlinear interpolation based Doppler elimination algorithm for array received signal， including single channel and single focus type， single channel and multi-focus type，and multi-channel and multi-focus type. The algorithm can compensate Doppler frequency shift and amplitude attenuation of radiated noise， and so improve the identification and position accuracy of noise source of moving target. The results of outside field test before and after using the Doppler elimination algorithm show that this algorithm can effectively eliminate the Doppler effect， and improve the position accuracy of noise source.

Doppler effect； noise source position； nonlinear interpolation

TJ630.34； TN911.7

A

1673-1948（2015）03-0177-06

2014-10-27；

2014-12-12.

姜成坤（1989-）， 男， 硕士， 主要研究方向为声信号处理技术.