基于交互式多模型的水下机动目标跟踪

高文娟，李亚安，陈　晓，陈志光

（西北工业大学 航海学院， 陕西 西安， 710072）

基于交互式多模型的水下机动目标跟踪

高文娟，李亚安，陈晓，陈志光

（西北工业大学 航海学院， 陕西 西安， 710072）

为了解决水下机动目标跟踪的实时性和可靠性问题， 在交互式多模型（IMM）的框架下对水下机动目标跟踪进行了分析， 建立了目标运动方程和观测方程。交互式多模型滤波算法的选择直接影响到跟踪的精度， 在跟踪滤波方面， 针对交互式多模型滤波过程中观测方程非线性对滤波性能的影响， 分别将扩展卡尔曼滤波（EKF）和无迹卡尔曼滤波（UKF） 2种滤波算法与交互式多模型算法相结合。仿真结果表明， 交互式多模型算法与UKF算法结合的滤波精度更高， 能够更有效、可靠地达到跟踪机动目标的目的。

水下机动目标； 交互式多模型（IMM）； 扩展卡尔曼滤波（EKF）； 无迹卡尔曼滤波（UKF）

0　引言

水下机动目标跟踪是指用声呐等传感器对目标进行观测， 并对所跟踪目标的运动状态进行建模、滤波、估计及预测的过程。近年来， 随着水声对抗技术和水下目标机动性能的不断完善， 现代水下武器系统所处的作战环境变得更加复杂［1］。目标机动形式不再局限于传统的蛇形机动和圆周机动， 出现了更加复杂的机动， 而已有的机动模型和跟踪算法在解决水下机动目标跟踪时会出现较多的误跟和失跟现象。因此， 研究新的机动模型和跟踪滤波方法显得极其重要。经过近几十年的发展， 机动模型和滤波算法获得了重要成果。就跟踪模型而言， Singer模型、半马尔科夫模型、“当前”统计模型（current statistical model， CSM）及交互式多模型等先后被提出［2］。由于实际水下战场环境复杂多变， 目标在运动过程中通常在各种运动状态之间频繁切换， 并不是保持单一的运动状态， 因此， 采用单模型跟踪会造成较大的跟踪误差。交互式多模型（interacting multiple model， IMM）［2-3］跟踪算法采用多个运动模型共同描述目标的运动状态， 在运算过程中， 根据各运动模型和目标运动过程的匹配程度， 系统为每个模型分配一定的概率，最终输出结果为模型跟踪结果的加权平均。当目标机动时， IMM算法能够重新分配模型概率， 改变混合输出结果， 因此， 跟踪效果远远优于单模型跟踪， 避免了跟踪丢失现象的发生［2］。IMM算法是近年来被广泛应用的一种有效的、性价比高的混合估计方法。水下目标机动时， 其观测方程和运动方程均为复杂的非线性方程， 给目标跟踪带来了困难。处理非线性滤波的经典方法是扩展卡尔曼滤波（extended Kalman filter， EKF）［4］，但该算法精度不高、稳定性差， 对目标机动反应迟缓。在强非线性时EKF违背局部线性假设， 可能会使滤波发散， 从而在跟踪中导致失跟和误跟。近年来， 针对强非线性问题， 出现了一种非线性滤波算法， 即无迹卡尔曼滤波（unscented Kalman filter， UKF）［5］， UKF是根据无迹变换（unscented transform， UT）和卡尔曼滤波相结合的一种算法， 通过非线性状态方程获得更新后的滤波值， 从而得到对机动目标的跟踪， 在跟踪中表现出跟踪精度高， 滤波效果好等特点。因此，UKF以其优越的性能受到了越来越多的关注，并得到广泛地应用。

根据水下机动目标跟踪的实时性和可靠性要求， 文中提出将EKF、UKF两种滤波方法应用到交互式多模型算法中， 通过仿真对算法的可靠性和准确性进行了分析， 结果显示将UKF与IMM算法结合能够更有效、可靠的对水下机动目标进行跟踪。

1　交互式多模型算法

IMM算法是在广义伪贝叶斯算法基础上提出的一种具有Markov转移概率的交互式多模型算法， 该算法具有很强的模块化特性， 针对不同的运动状态可以选择适应于该运动状态的目标运动模型来构建相应的运动模型， 有良好的跟踪特性， 因此得到了广泛的关注和较快的发展［6-7］。

1.1算法介绍

作为实时更新算法， IMM利用前一周期时刻的估计值计算当前目标的跟踪轨迹， 在一个IMM算法周期内， 包括了模型的输入交互、子模型滤波和预测、概率更新和融合输出4个步骤。

1） 输入交互

设从模型i转移到模型j的转移概率为Pij，则马尔科夫转移概率矩阵为

2） 子模型滤波及预测

3） 模型概率更新

模型j的概率更新如下

式中

4） 交互式输出

1.2IMM算法流程图

图1为在1个IMM算法周期内， 具有3个模型的IMM算法流程图。

图1　交互式多模型（IMM）算法流程图Fig. 1　Flow chart of interacting multiple model（IMM） algorithm

从图1中可以看出， IMM算法包含了1个交互式作用器、多个滤波器、1个模型概率更新器和1个估计混合器。针对不同的运动状态可以选择适应于该运动状态的模型来构建相应的跟踪模型， 共同相互作用来完成算法的实时更新。

2　适用于IMM的非线性滤波方法

卡尔曼滤波器估计［4-5］是1个用线性随机差分方程描述的离散时间过程的状态变量nx∈R，但大多数情况下， 状态变量和观测变量的关系是非线性的。

设非线性状态空间模型为

其中： 随机变量wk和vk代表过程激励噪声和观测噪声。差分方程式（13）中的非线性函数f将上一时刻k-1的状态映射到当前时刻k的状态， 驱动函数uk和零均值过程噪声wk是它的参数。观测方程（14）中的非线性函数h反映了状态变量xk和观测变量zk关系。

2.1扩展卡尔曼滤波（EKF）

Bucy、Sunahara等人在卡尔曼滤波的基础上提出并研究了EKF［2］， 并将EKF理论进一步应用到非线性领域。其基本思想是用泰勒展开式中的一次项对式（13）和式（14）中的非线性函数h和f进行线性化处理， 即先计算h和f的雅可比矩阵， 然后在标准卡尔曼滤波框架下进行递归滤波。

EKF算法和KF一样， 也分为2步： 预测和更新。其基本算法如下。

1） 预测

使用Jacobians矩阵更新模型

2） 更新

2.2无迹卡尔曼滤波（UKF）

传统非线性滤波的方法主要是EKF， 但该算法有着精度不高、稳定性差， 对目标机动反应迟缓等特点。近年来， 提出了一种非线性滤波算法，即UKF［5，8］， 它是根据UT变换和卡尔曼滤波相结合， 解目标后续时刻的预测值和量测值时， 则需要应用采样点计算， UKF通过设计加权点σ来近似表示n维目标采样点， 设计这些σ点经过非线性函数的传播， 通过非线性状态方程获得更新后的滤波值， 从而实现对目标的跟踪， 基本算法如下。

1） 设初值

2） 计算Sigma点

3） 时间更新

4） 量测更新

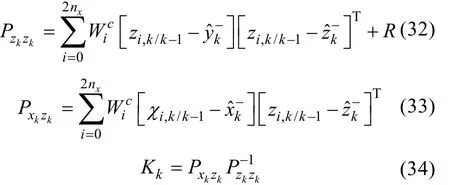
3　运动方程和观测方程

3.1运动方程

设状态向量

对于目标在做匀速直线运动时， 可以用CV模型对其进行跟踪， 状态方程

其中： uxuy为相互独立的零均值， 方差为2xσ2yσ的高斯白噪声； Wk是零均值的高斯白噪声序列；T是系统采样周期。

对于目标在匀速转弯运动时可以用CT模型对其进行跟踪， 状态方程

其中：

3.2观测方程

假定目标利用探测声呐探测目标的距离为R， 目标方位角为θ， 则观测方程为

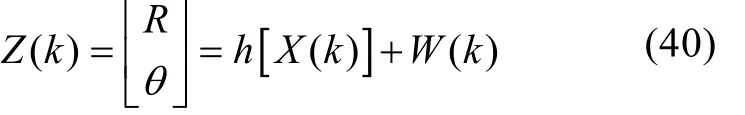
其中， W（ k）为零均值高斯白噪声， 误差协方差阵

4　仿真试验

4.1运动轨迹

仿真试验选用一种典型目标运动轨迹， 在IMM模型框架下分别对高斯观测噪声情况下的EKF和UKF算法性能作比较， 计算每个时刻机动目标的跟踪误差。目标运动轨迹包含： 匀速直线运动1+匀速转弯运动+匀速直线运动2。目标运动轨迹如图2所示。

图2　典型目标运动轨迹Fig. 2　Typical trajectory of a target

4.2仿真条件与结果

初始协方差为

模型初始转移概率为

应用EKF和UKF两种滤波器进行滤波， 结果如图3～图8所示。从图中可以看出， 对于强非线性系统， 不论是从位置跟踪误差还是从速度跟踪误差来看， UKF算法的跟踪效果明显比EKF算法好， 初始状态下UKF的滤波误差曲线迅速收敛， 波动远远小于EKF， 跟踪误差很小。这是因为EKF仅仅利用了非线性函数泰勒展开式的1阶偏导部分， 导致在状态的后验分布的估计上产生较大的误差， 从而影响了整个系统的性能。而UKF以UT变换为基础， 摒弃了非线性函数线性化的传统做法， 在卡尔曼线性滤波框架下， 对一步预测方程使用UT变换来处理均值和协方差的非线性传递， 省略了非线性的线性化过程， 因此非线性滤波的精度较高， 跟踪效果较好。由图7和图8可以看出， 不论是EKF还是UKF， IMM模型概率曲线都有很好的切换效果。

图3　扩展卡尔曼滤波（EKF）目标运动轨迹Fig. 3　Target maneuver trajectory with extended Kalman filter（EKF）

图4　无迹卡尔曼滤波（UKF）目标运动轨迹Fig. 4　Target maneuver trajectory with unscented Kalman filter（UKF）

图5　不同滤波算法的位置跟踪误差Fig. 5　Tracking errors of target position for different filtering algorithms

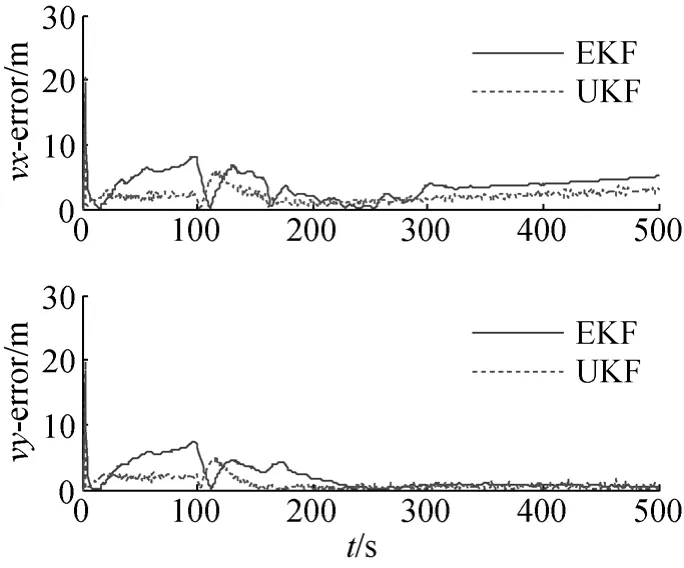
图6　不同滤波算法的目标速度跟踪误差Fig. 6　Tracking errors of target velocity for different filtering algorithms

图7　IMM-EKF模型概率曲线Fig. 7　Probability curves of the IMM-EKF model

图8　IMM-UKF模型概率曲线Fig. 8　Probability curves of the IMM-UKF model

5　结束语

文中以水下机动目标跟踪为实际应用背景，将EKF和UKF这2种非线性滤波方法引入到IMM算法中， 设计了IMM框架下的EKF和UKF 2种滤波算法。EKF的线性化忽略了泰勒展开式中的高阶项， 而UKF省略了非线性的线性化过程， 避免了该情况所带来的较大误差， 克服了跟踪精度不高、稳定性差的问题。仿真结果表明， 将UKF与IMM算法结合能够更有效、可靠的对水下机动目标进行跟踪， 对解决水下武器攻击目标这一难题有一定的参考价值。

［1］Mazor E， Dayan J， Averbuch A， et al. Interacting Multiple Model Methods in Target Tracking： A Survey［J］. IEEE Transactions On Aerospace and Electronic Systems， 1998，34（1）： 103-123.

［2］周宏仁， 敬忠良， 王培德．机动目标跟踪［M］. 北京： 国防工业出版社， 1991.

［3］Li X R， Jilkov V P. A Survey of Maneuvering Target Tracking-Part V： Multiple-Model Methods［J］. IEEE Transactions Aerospace and Electronic Systems， 2005， 41（4）：1255-1321.

［4］李彩菊， 李亚安. 扩展卡尔曼滤波与粒子滤波算法性能比较研究［J］．声学技术， 2009， 28（4）： 74-78.

Li Cai-ju， Li Ya-an. Research of Comparative Analysis of Extended kalman Filter and Particle Filter［J］. Technical Acoustics， 2009， 28（4）： 74-78.

［5］郭辉. 基于非线性滤波的目标跟踪算法研究［D］. 西安：西安电子科技大学， 2010.

［6］Bar-Shalom Y， Chang K C， Blom H A P. Tracking a Maneuvering Target Using Input Estimation Versus the Interacting Multiple Model Algorithm［J］. IEEE Transactions on Aerospace and Electronic Systems， 1989， 25（2）： 296-300.

［7］翟海涛. 基于IMM模型的目标跟踪算法［J］. 中国制造业信息化， 2010， 39（13）： 61-63.

［8］Sadeghi B， Moshiri B. Second order EKF and Unscented Kalman Filter fusion for tracking maneuvering targets［J］. IEEE International Conference on Information Reuse and Integration， 2007， 13（15）： 514-519.

（责任编辑： 杨力军）

Application of IMM to Underwater Maneuver Target Tracking

GAO Wen-juan，LI Ya-an，CHEN Xiao，CHEN Zhi-guang

（School of Marine Science and Technology， Northwestern Polytechnical University， Xi′an 710072， China）

For improving the real-time property and reliability of underwater maneuver target tracking， the interacting multiple model（IMM） algorithm is applied to underwater maneuver target tracking. Based on the IMM algorithm， a target maneuvering model and a measurement model are established. Because the tracking accuracy depends on filtering method， the extended Kalman filter（EKF） and the unscented Kalman filter（UKF） are combined with the IMM algorithm，respectively. Simulation shows that the IMM algorithm combined with UKF can achieve higher filtering accuracy， hence can track maneuver target more effectively and reliably.

underwater maneuver target； interacting multiple model（IMM）； extended Kalman filter（EXF）； unscented Kalman filter（UKF）

TJ630.34； TB566

A

1673-1948（2015）03-0196-06

2015-01-15；

2015-04-02.

国家自然科学基金（51409214）

高文娟（1990-）， 女， 在读硕士， 主要研究方向为水下目标跟踪.