实际气体压缩机气阀运动评估与弹簧力校核的简易方法

吴 双，潘树林，康 慧，吴四建

(1.湖南人文科技学院能源与机电工程学院，湖南 娄底 417000；2.宝鸡市博磊化工机械有限公司，陕西 宝鸡 721300)

1 引言

压缩机气阀设计时，应分析气阀运动规律并校核气阀弹簧力。良好的气阀运动规律要求：气阀及时开启、及时关闭，并有较长的全开期[1]，因此气阀应采用合适的弹簧力。当弹簧力过大时，气阀运动呈颤振型，导致气阀时间截面减小，阻力损失增加[2]，气阀提前关闭，压缩机压力系数与排气量变小[3]。当弹簧力过小时，气阀延迟关闭，压缩机泄漏系数与排气量变小[2，3]。弹簧力过大与过小都会引起气阀使用寿命下降[2]。

国内一般压缩机与压缩机气阀企业进行气阀设计时，通常把工质当做理想气体考虑，采用戴维斯方法评估气阀运动，以校核气阀弹簧力是否合适[4]。当工质压力较高、温度较低，接近临界状态时，实际气体与理想气体差别较大[5]，此时采用戴维斯方法评估气阀运动与校核弹簧力时，应把工质当做实际气体考虑。

2 理想气体的戴维斯方法

图1为典型的阀片位移时间曲线，其横坐标为曲轴转角，纵坐标为阀片位移，图1中有3个曲轴转角参数θ1、θ2、θ3[4，6]。θ1为气阀假想关闭角，即假定无气流推力时，阀片仅在弹簧力推动下，从全开状态到关闭状态所需时间对应的曲轴转角。θ2为阀片刚开始脱离升程限制器到活塞到达止点，期间所对应的曲轴转角。θ3为阀片到达升程限制器到活塞到达止点，期间所对应的曲轴转角。

图1 阀片运动时的3个特征角

采用戴维斯方法评判气阀运动时，曲轴转角参数θ1、θ2、θ3要满足如下条件：θ2/θ1>2，同时θ2/θ3<0.7[4，6]。θ2/θ1>2意味着气阀能及时关闭，θ2/θ3<0.7意味着气阀有较长的全开期。

θ1较容易计算，其计算公式如下[6]

(1)

式中θ1——特征角，°

ns——转速，r/min

M——气阀当量运动质量，kg

Kz——弹簧总刚度，N/m

H——气阀升程，m

H0——弹簧预压缩量，m

阀片刚开始脱离升程限制器时，气流推力等于弹簧力，得如下关系式[6]

Kz(H+H0)=βAsΔpv

(2)

式中β——气阀全开时气流推力系数

As——阀座出口处通流面积，m2

Δpv——气流流经气阀时的压力降，Pa

进气阀或排气阀工作过程中，认为气体密度不变，活塞扫过的气体体积都经进气阀流入或经排气阀流出[6]，则

(3)

式中ρ——流过气阀的气体密度，kg/m3

Ap——活塞面积，m2

v——活塞速度，m/s

N——同侧同名气阀个数

Ae——单个气阀的有效通流面积，m2

vm——活塞平均速度，m/s

θ——曲轴转角，°

λ——曲柄半径与连杆长度之比

当流过气阀的工质为理想气体时，根据气体状态方程，得

(4)

式中p——流过气阀的气体压力，Pa

R——气体常数，J/(kg·K)

T——流过气阀的气体温度，K

把式(4)、式(3)代入式(2)，得

(5)

由式(5)可求得θ。在向轴行程中，θ2=180°-θ，在向盖行程中，θ2=360°-θ，由此得到θ2[6]。

考虑到阀片从开始开启到全开这段时间很短，因此θ3可近似为阀片从开始开启至活塞达到止点，期间所对应的曲轴转角[6]。定义气阀开始开启时的曲轴转角为开启角θv。对于盖侧进气阀与轴侧排气阀而言，θ3=180°-θv；对于盖侧排气阀与轴侧进气阀而言，θ3=360°-θv[6]。

对进气阀而言，当θ=θv时，缸内余隙容积中气体膨胀后，其压力等于名义吸气压力。对排气阀而言，当θ=θv时，缸内气体压缩后，其压力等于名义排气压力。当工作介质为理想气体时，可得如下关系式[6]

(6)

(7)

(8)

(9)

式中α——相对余隙容积

ε——名义压比

m——膨胀过程指数

n——压缩过程指数

θv——开启角，°

上面各公式中，式(6)用于计算盖侧进气阀开启角，式(7)用于计算轴侧进气阀开启角，式(8)用于计算盖侧排气阀开启角，式(9)用于计算轴侧排气阀开启角。

3 实际气体的戴维斯方法

实际气体压缩机仍然采用戴维斯方法评估气阀运动与校核气阀弹簧力。气阀假想关闭角θ1仍然采用式(1)计算。

实际气体状态方程如下[5]

(10)

式中Z——气体压缩因子

把式(10)、式(3)代入式(2)，得

(11)

由式(11)得到θ后，同样，在向轴行程中，θ2=180°-θ，在向盖行程中，θ2=360°-θ，得到实际气体压缩机气阀的θ2。

分析实际气体压缩机膨胀过程与压缩过程时，与前面理想气体压缩机一样，膨胀过程与压缩过程均不考虑泄漏，按定质量处理[4]。对进气阀而言，排气终了后，当余隙容积中的气体膨胀到名义吸气压力时，此时曲轴转角为进气阀开启角。对排气阀而言，吸气终了后，当工作腔内气体压缩至名义排气压力时，此时曲轴转角为排气阀开启角。根据膨胀过程与压缩过程中实际气体质量不变，得

(12)

(13)

(14)

(15)

式中V0——余隙容积，m3

pd——名义排气压力，Pa

Td——排气温度，K

Zd——排气状态下压缩因子

x——活塞位移，m

ps——名义吸气压力，Pa

Ts——吸气温度，K

Zs——吸气状态下压缩因子

对实际气体压缩机而言，压缩机排气温度Td的计算较复杂。考虑到压缩机工作介质当做实际气体时，气体压力较高，此时压缩机工作循环中，膨胀过程与压缩过程均可以当做等熵过程[4]。 求实际气体压缩机排气温度时，先由压缩机名义吸气压力、吸气温度可查得实际气体的熵，再由该熵、名义排气压力可查得排气温度[5]。

上面各公式中，式(12)用于计算盖侧进气阀，式(13)用于计算轴侧进气阀，式(14)用于计算盖侧排气阀，式(15)用于计算轴侧排气阀。在式(12)～(15)中代入活塞位移x计算公式，整理得

(16)

(17)

(18)

(19)

上面各式中，由式(16)得到盖侧进气阀开启角，θ3=180°-θv；由式(17)得到轴侧进气阀开启角，θ3=360°-θv；由式(18)得到盖侧排气阀开启角，θ3=360°-θv；由式(19)得到轴侧排气阀开启角，θ3=180°-θv。

用实际气体的戴维斯方法评估实际气体压缩机气阀运动与校核气阀弹簧力过程中，各特征角计算公式的求解方法与理想气体的戴维斯方法相同。

4 压缩因子对气阀运动与弹簧力的影响分析

当压缩机工作介质压力较高、温度较低，接近临界状态时，工作介质应当做实际气体考虑。大多数气体的临界压缩因子仅在0.23～0.3间[5]。以常见的二氧化碳为例，其临界压力为7.38 MPa，临界温度为31.1 ℃，临界压缩因子为0.275。采用戴维斯方法评估二氧化碳等高压压缩机的气阀运动与校核气阀弹簧力时，必须考虑压缩因子的影响。

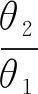
由式(11)可知，当特征角θ2一定时，需要的气阀弹簧力与压缩因子成反比，即压缩因子越小，需要的气阀弹簧力越大。如压缩机吸气或排气状态下，气体压缩因子为0.5时，考虑压缩因子后，要使特征角θ2保持不变，需要气阀弹簧力翻倍。

由式(16)～(19)可知，当Zs=Zd，即排气状态与吸气状态下压缩因子相等时，压缩因子对特征角θ3没有影响。当Zs>Zd时，由式(16)、(17)可知，吸气阀开启角变大，吸气阀特征角θ3变小。当Zs>Zd时，由式(17)、(18)可知，排气阀开启角同样变大，排气阀特征角θ3变小。

5 结论

(1)采用实际气体的戴维斯方法评估实际气体压缩机气阀运动与校核气阀弹簧力简易、方便，比理想气体的戴维斯方法可靠。

(2)当压缩因子较小时，气阀特征角θ2较小，气阀易出现延迟关闭现象。

(3)当吸气状态压缩因子大于排气状态压缩因子时，气阀特征角θ3变小。

(4)当压缩因子较小时，为避免延迟关闭，气阀设计应采用较大的弹簧力。