初中几何教学中习题变式的应用探析
陈立庚
【内容摘要】初中几何是一门相对复杂的学科,解题往往需要灵活运用已掌握的知识。习题变式是一种具有较高实用性的教学方法,应用在初中几何教学中能够起到“化繁为简”的效果,对提高学生的几何能力有着十分重要的积极意义。
【关键词】初中几何 习题变式 应用探讨
前言
几何教学是初中教育的重要内容,关系到学生的数学能力培养。作为教学成果重要影响因素之一的教学方法,无疑是其中最需要变革的部分。习题变式经过了大量的教学实践验证,应用在初中几何教学中能够显著改善教学成果。
一、习题变式简述
1.含义
习题变式的关键在于“变”,指的是对教学中的习题在解题思路、切入点等方面进行转换,以达到“化简”习题的目的,转换之后的问题本质没有发生改变,因此,学生可以借助这个过程寻找解题方法。习题变式在初中几何中的应用,可以转换的内容有解题方法、结论等。
2.作用
习题变式在初中几何中应用的作用主要体现在两个方面:(一)改善初中几何教学成果。习题变式应用在教学中,能够帮助学生抓住问题的本质,通过合理的问题转化,一步步的简化题目。在习题变式教学的过程中,教师可以通过一道题目的讲解,使学生掌握此类题目的解题思路,事半功倍。(二)提高学生的数学能力。有不少的老师在教学中态度相对消极,使用的解题方法相对单一,对学生的思维形成了限制。习题变式在初中几何中的应用,可以使学生更全面的了解问题、思考问题,形成灵活的思维模式,有助于学生知识运用能力的提升。
3.在初中几何教学中的应用原则
习题变式作为一种科学的教学方法,应用在初中几何教学中取得了良好的效果,但在其应用中,应注意遵循一定的原则:(一)针对性原则。习题变式在教学中的应用应考虑到课堂性质的差异,遵循针对性原则,确保有效应用。(二)合理原则。习题变式的“变”,应围绕所学知识进行有理有据的合理转变,为解题服务。(三)共同参与原则。教师应转变传统的填鸭式教学模式,积极鼓励学生参与课堂教学。同时,习题变式教学能够使学生更好的把握问题本质,掌握“变式”的规律和方法,提高其创新能力。
二、初中几何教学中习题变式的应用探讨
1.转变题型
在实际的几何教学中,题目类型通常也就是选择和填空、解答等,在讲解题目时,对于某些题目,教师可以依据其特点,将其合理转换为其他题型,采用灵活的解题方式,使学生掌握问题实质。
例题:某个等腰三角形,已知条件为其中两边长度分别为5cm、10cm,求其周长。
经过习题变式,可以将其转换为:
某个等腰三角形,已知其中两边长分别为5cm、10cm,那么其周长应为( )cm。
A.25 B.20
C.15或25 D.25或25
2.转变方法
大多数几何习题的解题方法并不唯一,切入点不同,使用的方法也存在差异。对于相同或相似的题目,从不同的角度理解或解题思路不同,解题方法也就存在很大差异。习题变式在初中几何中的应用,能够丰富题目的解法,使学生更全面的掌握几何知识。
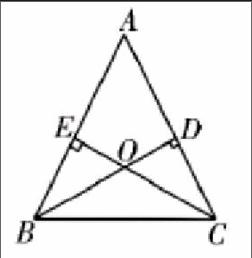
例题:已知等腰三角形△ABC,BD为AC边上的高,CE为AB边上的高,证明BD=CE。
解题方法1:
已知:△ABC等腰三角形,且BD、CE分别为两腰上的高
由此可得:AB、AC相等,且∠AEC 与∠ABD均为直角
所以:△ABD全等于△ACE,BD=CE
解题方法2:
等腰△ABC面积=AB·CE/2=AC·BD/2,同时,又因为AB、AC相等,所以BD与CE也是相等的。
3.转换结论
初中几何相对来说具有一定的难度,在解题过程中,为了将题目化简,方便解答,必要时可以将结论进行合理的转换。习题变式能够使学生透过表层问题探寻本质,对于学生知识运用能力的提高有着重要意义。
例题:已知两个等边三角形ABD、BCE,其中,A点、B点和C点在同一条线上,将C、D相连,与BE交点为G,将A、E连接,与BD交点为F,将F点与G点连接起来,证明AE=CD。
经过习题变式,可以将此题结论转化为以下两种:

