样例的概念属性呈现方式对初一学生分式概念学习的影响

甘卫群，刘万伦

（浙江师范大学　教师教育学院，浙江　金华　321004）

样例的概念属性呈现方式对初一学生分式概念学习的影响

甘卫群，刘万伦

（浙江师范大学教师教育学院，浙江金华321004）

样例学习就是通过样例来学习的一种学习方式.样例学习能够提高学生学习的自主性，培养其独立探究、主动获取知识的能力.研究选取164名初一学生作为被试，探讨样例中概念属性的两种呈现方式（概念属性分步呈现、概念属性综合呈现）对初一学生分式概念学习效果的影响.结果表明：样例能够有效促进学生分式概念的学习；概念属性分步呈现条件下的样例学习效果比综合呈现条件下的要好，两者差异达到显著水平.

样例学习；概念学习；概念属性；呈现方式

1　问题提出

样例学习（leaning from example or example study），就是从样例中学习，通过样例来学习的一种学习方式（马俊青，2009）.样例学习能够提高学生学习的自主性，培养其独立探究、主动获取知识的能力.

20世纪50、60年代，研究者开始用样例学习来研究概念的形成，到70年代中期，有很多研究者运用样例学习研究知识的学习（陈云儿，2004）.到20世纪80年代，Sweller提出认知负荷理论（Sweller. J，1988），他认为，如果在练习题之前呈现样例，学习者解决问题的效率会大大提高，因为样例给学习者提供了专家解决问题的方法，大大降低了学习者的认知负荷.之后很多研究者对样例在课堂教学中使用的有效性进行了研究，称之为“样例学习研究”，其主要涉及3方面的内容：样例内特征（intra-example feature）的研究、样例间特征（inter-example feature）的研究、样例与学习者之间的相互作用的研究.样例内特征的研究指的是对样例自身进行设计的研究，主要体现在：（1）提供样例的多个信息源能够降低学习者的认知负荷，提高学习效果（Mousavi, Low & Sweller, 1995）；（2）提供样例的多种表征形式能够促进学习者的样例学习效果（Jeung，Chandle & Sweller，1997）；（3）子目标编码能促使学习者达到更好的学习效果（Catrambone & Holyoak，1994，1995，1996；Catrambone & Holyoak，1990）.样例间特征的研究指的是对样例与样例之间的一些特征与联系进行设计的研究，主要体现在：（1）样例数量的研究：研究证明学习者若要较好地掌握一个知识点，一般情况下需要两个及以上的样例；（2）样例变异性的研究：有研究表明，变异性高的样例组中的学习者问题解决迁移的成绩要比变异性低的样例组中的学习者的成绩高（Paas，1994；宁宁、喻平，2010）；（3）练习题与样例的呈现方式：呈现方式是指分块式和交互式.研究表明，交互式呈现方式更加有利于学习者的学习效果（唐学峰、莫雷，2004；刑强、莫雷，2005；赵红，2007）.样例与学习者之间的相互作用的研究主要是指样例学习的自我解释效应.自我解释（self-explaining）是学习者经常用来帮助自己理解,并以“问题”或“判断”等各种形式呈现外部信息的加工过程，是一种由自我产生并指向自我知识建构的心理活动（连四清、增辉，2011）.很多研究已经表明有效的自我解释能够更好地促进样例学习效果（Renkl & Atkinson，2002，2003；连四清、增辉，2011；史月杰，2014）.

以上3种样例设计形式在数学学科的样例学习研究中都有涉及.数学学科中的样例学习是通过设计有效样例，让学生通过学习样例提高他们对数学问题的解决能力.具体包括两方面：其一是让学生从样例中习得隐含的规则、原理，进而将规则、原理用到相似的具体题目中；其二是让学生读懂样例的解题过程，通过模仿样例解题方法去解决练习题，进而掌握该类问题的解决方法.研究者从第一方面的研究领域得到启示，既然学生能够习得样例中的规则、原理，进而将规则、原理运用到相似的具体题目中去，那学生是否也能够从样例中习得数学概念的本质属性，进而归纳出数学概念呢？另外，之前的样例学习研究都是从宏观上设计样例，他们的着眼点是整个样例，即从整体上设计样例，而没有进一步考虑样例中所隐含的微观属性.该研究首次从数学概念的本质属性（即微观层面）着手设计样例，探讨概念属性呈现方式对样例学习的影响.

2　方　法

2.1实验目的

该实验主要考察初一学生在样例中的概念属性分步呈现条件下分式概念学习的效果是否比综合呈现条件下的要好.

2.2实验假设

（1）假设1：样例学习是学生进行分式概念学习的有效方式.

（2）假设2：样例的两种概念属性呈现方式对学生分式概念学习的效果产生不同的影响，其中概念属性分步呈现条件下学生分式概念学习效果要比综合呈现条件下好.

2.3被试

选择金华市某初中的初一学生为被试，学生还没有进行分式章节的相关学习.通过前测，选出能够正确完成前6道关于整式的习题而不能正确完成后3道关于分式的习题的164名学生作为正式被试.按照上个学期期末考试的数学成绩，将被试分为数学知识水平相同的两个平行组，每组82人.收回数据之后，剔除了一些无效数据，把它们判为无效数据的指标为：（1）即时后测与延迟后测成绩均低于6.5分的被试被视为处于随机猜测水平，故剔除；（2）有些被试即时后测成绩不是很理想，处于7分到10分之间，但是延迟后测的成绩竟然接近满分15分，研究者认为这样的被试在延迟后测过程中出现了作弊行为，这样的数据也被剔除.这样，最终有效被试为156人，其中概念属性分步呈现组为79人，概念属性综合呈现组为77人.

2.4实验设计

该实验采用单因素实验设计，其中自变量是样例中的概念属性呈现方式（概念属性分步呈现、概念属性综合呈现）.分步呈现是指一个样例题中只包含分式概念的其中一个属性，综合呈现是指一个样例题中包含分式概念的全部3个属性（分母有未知数、分母不为0、分子分母均要求为整式），因变量是学习者分式概念学习后的测验成绩（包括即时后测成绩、延迟后测成绩），控制变量是学习者的原有数学知识水平.

2.5实验材料

实验材料分为前测材料、学习材料、练习材料、即时测验材料和延迟测验材料.所有材料的题目均由实验者在心理学专家及实验所在学校的几位初一数学老师的指导下确定.实验过程中材料均由A4纸呈现.

（1）前测材料：前测材料共9道题，其中前6道题是关于整式基本知识的习题，后3道是关于分式基本知识的习题.题型分别为单选题、多选题和填空题.

（2）学习材料：学习材料分为两种，一种为概念属性分步呈现的样例材料，另一种为概念属性综合呈现的样例材料.每种属性呈现方式的样例分为3个学习单元，其中单元一和单元三的样例题型均为1道单选题和1道多选题，单元二样例中概念属性分步呈现的样例题型为2道简答题，样例中概念属性综合呈现的样例题型为1道选择题和简答题结合在一起的综合题（先选出分式，然后再解答该分式中的字母满足什么条件时分式有意义，分式中的字母满足什么条件时分式无意义）.

样例属性分步呈现的样例材料的每个单元的例题只涉及分式概念的其中一个属性，比如：

例：下列各式中，其中是分式的是（ C ）单选

这个题目只考察分式概念中的其中一个属性——分母有未知数.

概念属性综合呈现的样例材料的每个单元中的每个题目都涉及分式概念所具备的3个属性，比如：

例：下列各式中，属于分式且分式有意义的是（ D ）单选

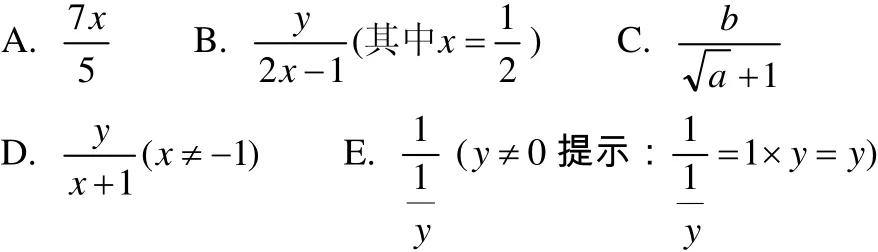
这个题目的A选项考察的是分式概念中要求分母有未知数这个属性；B这个选项考察的是分式概念中要求分母不为0这个属性；C、E这两个选项考察的是分式概念中要求分子、分母都为整式，既不能是根式，也不能是分式.选项D是正确答案.

（3）练习材料：每个单元的练习材料和该单元学习时的样例材料在题型、题数及难度上均保持一致.

（4）后测材料：后测材料分为即时后测材料和延迟后测材料，是两份平衡测验，难度系数一样.每种后测材料均包括4道单选题、2道多选题和2道简答题.

2.6实验程序

整个实验过程由实验者和3位心理学研究生来当主试，实验前对3位研究生进行过严格培训，他们都已经熟练掌握了实验流程.实验在安静的教室中分组进行，教室中除了主试和被试没有其他闲杂人士干扰.

实验程序分3个阶段：

前测阶段：通过前测（施测时间为15分钟）选出164名能够正确完成前6道关于整式基本知识的习题但不能答对后3道关于分式基本知识的习题的学生作为被试正式参加实验.然后根据上个学期的数学期末成绩，将被试者分为数学知识水平相同的两平行组.

样例学习阶段：由于每个实验组有82人，人数有点多，故将每个实验组分为4个小组进行施测.

样例学习过程中，首先发给被试一个单元的两道样例题，首先提示被试在相应的位置写上班级和姓名，然后主试读指导语，指导语为：“各位同学，你们好，这是一个关于通过样例的形式进行分式概念自主学习的一个实验，请大家认真阅读试卷上的两道样例题，相互之间不要有任何讨论，若已经读懂请举手示意！”主试等一组中的所有被试都举手表示读懂了，或者还有部分被试没有举手，但时间已经为5分钟了，则收回样例题，接下发给被试2道跟样例题在题型和难度上一致的练习题，指导语为：“通过刚才的学习，请大家认真、独立的完成下面2道练习题，相互之间不要有任何讨论，做好请仔细检查，若确定无误了请举手示意！”等一组中的全部被试都举手表示完成时，或者还有部分被试没有完成但时间已经过去5分钟，主试收回练习题.第一个单元学习结束，紧接着继续学习后面两个单元的样例题，实验程序及指导语同单元一.等3个单元都学习完，最后实验者呈现分式概念的定义.整个样例学习阶段时间为30分钟.

后测阶段：后测分为即时后测与延迟后测.即时后测在样例学习结束后休息5分钟进行施测，时间为15分钟；延迟后测在样例学习结束后的第12天进行施测，时间也为15分钟.

2.7计分标准与统计分析工具

单选题每道1分，4道共4分；多选题每道题有7个选项，按照判断题的要求给分，每个选项判断正确得0.5分.（正确的选项选上或不正确的选项没有选上，都得分；选错或正确的没选上，都不得分）一道题3.5分，两道题共7分；最后4道简答题每道1分，共4分.故测验卷满分为15分.数据输入SPSS17.0进行统计分析.

3　结　果

3.1样例学习的效果

为了解初一学生样例学习的效果，将后测成绩≥6.5分的学生视为通过样例学习，计算其通过率，见表1.

表1　样例学习的效果

从表1可知，样例学习的学生中通过人数为156人，通过率为95.1%，比例较高，说明样例学习是初一学生分式概念学习的有效方式.

3.2学生在概念属性不同呈现方式下分式概念学习效果的

基本情况

为了解学生在概念属性的不同呈现方式下分式概念学习的基本情况，计算了各种条件下即时后测与延迟后测的平均数与标准差，见表2.

表2　概念属性不同呈现方式下分式概念学习的基本情况

从表2可知，不管是即时后测还是延迟后测，被试在概念属性分步呈现条件下的后测成绩（即时后测：M=12.779，延迟后测：M=12.798）均要比在综合呈现条件下的高（即时后测M=11.695，延迟后测：M=11.831）.这说明概念属性呈现方式对初一学生进行分式概念学习的效果是有影响的，其中概念属性分步呈现更加有利于初一学生进行分式概念的学习.

3.3概念属性呈现方式对初一学生分式概念学习效果的影响

为了解初一学生在概念属性的两种呈现方式条件下分式概念学习的效果是否存在差异，分别对即时后测与延迟后测中的两种呈现方式下的成绩进行差异的显著性检验，见表3.

表3　概念属性呈现方式对分式概念学习的影响

从表3可知，不管是在即时后测中，还是在延迟后测中，学生在样例的两种呈现方式下进行分式概念学习的效果均存在显著差异.表2显示，学生在概念属性分步呈现条件下分式概念学习成绩的平均数（即时后测：M=12.779，延迟后测：M=12.798）要比在综合呈现条件下的高（即时后测M=11.695，延迟后测：M=11.831），两个数据结合说明样例中的概念属性呈现方式对学生进行分式概念学习的效果是有影响的，其中学生在概念属性分步呈现时进行分式概念学习的效果要比在综合呈现条件下的好，并且两者差异达到显著水平.

3.4概念属性的不同呈现方式下分式概念学习的保持效果

为了解两种呈现方式对学生的分式概念学习效果是否具有保持效果，分别对不同呈现方式条件下的学生的即时后测与延迟后测成绩进行差异的显著性检验，见表4.

表4　不同呈现方式下分式概念样例学习的即时后测与延迟后测的差异

从表4可知，概念属性分步呈现（p=0.930）和概念属性综合呈现（p=0.513）的即时后测与延迟后测之间的成绩差异均没有达到显著水平，说明这两种呈现方式对初一学生分式概念学习来说，均具有良好的保持效果.

4　讨　论

4.1通过样例进行分式概念学习的效果

以往研究表明，学生可以通过样例学会概念，但是那时候用样例来研究概念形成的研究对象都是人工概念，最具有代表性的是布鲁纳的人工概念形成.通过样例学习来探讨分式概念的样例学习效果，由表1可知，学生样例学习的通过率为95.1%，这说明了学生是可以通过样例学会分式概念的.样例学习理论认为，样例给学生提供了一个典型的参考，学生通过对样例的学习，心里已经形成了分式概念的大概涵义，等样例学习结束之后，实验者向学生呈现分式概念的定义，这不但对学生前期样例学习过程中已经形式的概念进行对、错的检验，同时也对学生已经掌握的概念进行强化，从而更好地促使他们分式概念学习的效果.再加上该实验设计的材料是选择题和简答题，选择题中的选项可以让学生通过横向比较，利用假设检验法得出题中涉及的分式概念属性；简答题的内容是问学生下列分式在什么情况下有意义？在什么情况下无意义？目的是为了让学生明白分式要成立且有意义，分母必须不为零.其解法为学生提供了专家解决问题的方法，使他们快速地明白分式有意义时应该成立的前提条件.该研究表明样例学习是学生有效掌握分式概念的途经.

4.2样例的概念属性呈现方式对分式概念学习效果的影响

以往研究对样例所进行的设计都是着眼于整个样例，即是从宏观层面考虑去如何设计一个有效的样例，该实验鉴于数学概念的特点，首次从微观层面（样例中的概念属性）入手来设计有利于学生分式概念学习的样例.该研究利用样例让学生进行分式概念学习，关键是让学生归纳总结出样例中所涉及的分式概念属性，学生一旦明白分式概念所包含的全部属性也就掌握了分式概念.

通过对样例呈现方式对学生分式概念学习效果的影响进行t检验可得，不管是即时后测还是延迟后测，学生均是在概念属性分步呈现条件下进行分式概念学习的效果要比在综合呈现条件下的好，与实验假设相符.原因是，因为学生的认知资源是有限的，在同一时间内，如果需要接受的知识量太多，便会给学生的工作记忆造成太大的负担，从而影响学习效果.概念属性分步呈现时，一个单元中的两个题目均只涉及分式概念的其中一个属性且是同一个属性，学生在学习这两个样例时只需要归纳总结出概念的一个属性即可；而概念属性综合呈现时，一个单元中的两个题目均涉及分式概念的全部3个属性，理想状态下，学生在学习这两个样例时需要归纳总结出概念的全部3个属性.认知负荷理论认为，学生的认知负荷总量是有限的，包括内在认知负荷、外在认知负荷和有效认知负荷.相对于概念属性综合呈现条件，学生在概念属性分步呈现条件下进行分式概念学习时的外在认知负荷较低，有效认知负荷较高，他们不需要花太多的时间来理解材料中所涉及的知识点，学习起来较轻松，所以概念学习的效果也会较好.以往也有很多研究着眼于如何设计有效的样例来降低学生的外在认知负荷，提高学生的有效认知负荷，从而提高他们的样例学习效果，比如，文本信息与图示信息的整合、听觉信息与视觉信息的整合、样例题与练习题的呈现方式采用交互式等.

5　教学建议

5.1教师在数学概念教学中可适当利用样例

以上研究证明样例能够有效促进学生分式概念的学习，教师在教授数学概念时，可以改变以往那种“一个定义，三项注意”的教学方式，这种教学方式只会让学生对数学概念进行机械记忆，而没有真正弄懂概念的内涵，导致学生虽然课堂上记住了概念的定义，也会按照定义的要求去解答课堂上的题目，但是过一段时间就会忘记了该概念的定义，也难以对知识点进行灵活迁移，题目稍微有变化就会出错.而通过样例进行概念学习，学生可从样例中自行归纳出概念所包含的本质属性，印象比较深刻.另外样例给学生提供了一个典型的参照，使这些文字式的抽象概念具体化，从而能够使学生更好地掌握概念.

5.2教师在设计数学概念的样例时应多采用属性分布式

根据认知符合理论，学生的认知负荷总量是不变的，包括内在认知负荷、外在认知负荷以及有效认知负荷.内在认知负荷是指工作记忆对学习材料的难度及复杂性进行认知加工时所引起的认知负荷，外在认知负荷是指工作记忆对学习材料不恰当的组织和呈现形式进行加工时所引起的认知负荷，有效认知负荷是工作记忆对学习材料恰当的组成和呈现形式进行加工时所引起的认知负荷.内在认知负荷是没法改变的，而外在认知负荷和有效认知负荷都可以做到适当的降低或升高.教师在设计样例时应该根据认知负荷理论，尽量降低外在认知负荷、提高有效认知负荷，从而提高学生的样例学习效果.

大家都知道，一个数学概念都包含好几个本质属性，如果一个样例题中包含该概念的所有属性，这便会大大加大学生的外在认知负荷，故教师在设计样例题时，可适当减少一个样例题中所包含的概念属性个数，使学生在掌握了概念中的一个属性或者部分属性的前提下，再继续掌握其它的属性，直到掌握全部的概念属性，这样便会大大降低学习者的外在认知负荷，从而提高了有效认知负荷.

6　结　论

（1）样例能够有效促进学生分式概念的学习.

（2）学生在概念属性分步呈现条件下的样例学习效果要比在综合呈现条件下的好.

[1]马俊青.数学样例学习与学生数学知识形成关系的研究[J].数学教育学报，2009，18（4）：69.

[2]陈云儿.以合作方式学习样例的研究[D].华东师范大学，2004.

[3]Sweller J. Cognitive Load during Problem Solving: Effects on Learning [J]. Cognitive Science, 1988, 12(2): 257-285.

[4]Mousavi S Y, Low R, Sweller J. Reducing Cognitive Load by Mixing Auditory and Visual Presentation Modes [J]. Journal of Educational Psychology, 1995, 8(7): 319-334.

[5]Jeung H, Chandler, P Sweller J. The Role of Visual Indicators in Dua1sensory Mode Instruction [J]. Educational Psychology: Learning, Memory, and Cognition, 1997, 8(7): 252-259.

[6]Catrambone, R. Improving Examples to Improve Transfer to Novel Problems [J]. Memory & Cognition, 1994, 22(5): 606-615.

[7]Catrambone R. Aiding Subgoal Leaming: Effects Ontransfer [J]. Journal of Educational Psychology, 1995, 87(1): 5-17.

[8]Catrambone R. Generalizing Solution Procedures Learned from Examples [J]. Journal of Experimental Psychology: Learning, Memory, and Cognition, 1996, 22(4): 1 020-1 031.

[9]Catrambone R, HOlyoak K J. Learning and Subgoals and Methods for Solving Probability Problems [J]. Memory & Cognition, 1990, 18 (6): 593-603.

[10] Paas F, Van Merrienboer J. Variability of Worked Examples and Transfer of Geometrical Problem-Solving Skills: A Cognitive-Load Approach [J]. Journal of Educational Psychology, 1994, 86(1): 122-133.

[11] 宁宁，喻平.多重变异性数学样例对迁移影响的初步研究[J].数学教育学报，2010，19（6）：50-52.

[12] 唐学峰，莫雷.表面内容不同方面相似性对样例迁移的影响[J].心理科学，2004，（4）：631-633.

[13] 邢强，莫雷.多重样例的变异性和编码对迁移影响的实验研究[J].心理科学，2005，（6）：1 382-1 387.

[14] 赵弘.样例的变异性对问题解决迁移的影响[J].辽宁师范大学学报（社会科学版），2007，（4）：46-48.

[15] Renkl A, Atkinson R K, Maier U H. From Example Study to Problem Solving: Smooth Transitions Help Learning [J]. The Journay of Experimental Education, 2002, 70(4): 293-315.

[16] Renkl A, Atkinson R K. Structuring the Transition from Example Study to Problem Solving in Cognitive Skill Acquisition: A Cognitive Load Perspective [J]. Educational Psychologist, 2003, 38(1): 15-22.

[17] 连四清，增辉.自我解释对等差数列概念和通项公式远近迁移的影响[J].数学教育学报，2011，20（2）：23-25.

[18] 史月杰.样例的呈现方式对学生学习排列知识的影响的实验研究[J].数学教育学报，2014，23（2）：69-72.

Effects of Concept Property Presentation in the Example on Fraction Concept Learning of Grade One Junior High School Students

GAN Wei-qun, LIU Wan-lun
(College of Teacher Education, Zhejiang Normal University, Zhejiang Jinhua 321004, China)

Example learning is a way of learning throng example which can improve students’ autonomy of learning, cultivate students’ Independent inquiry and the ability of Taking the initiative to acquire knowledge. This study selected 164 grade one junior high school students as subjects to discuss the effects of two concept property presentations in the example (concept property stage presentation, concept property comprehensive presentation) on fraction concept learning effect of grade one junior high school students. The results show that: the example can effectively promote learners’ fraction concept learning; the fraction concept learning effect on the condition of concept property stage presentation is better than that of comprehensive presentation, and the difference reaches significant levels.

example learning; concept learning; concept property; presentation

G420

A

1004–9894（2015）06–0068–05

[责任编校：周学智]

2015–08–12

浙江师范大学教师教育研究基地课题——小学生外显与内隐类别学习的发展特点（ZC322012009）；浙江师范大学人文社科重点研究项目——基于规则与信息整合类别学习的内部机制（KYJ06Y12009）

甘卫群（1988—），女，浙江台州人，硕士研究生，主要从事数学概念学习研究．刘万伦为本文通讯作者．