问题情境对学生建构有理数加法法则影响的差异性研究

陈丽敏，景　敏

（1．沈阳师范大学　辽宁省基础教育教研培训中心，辽宁　沈阳　110034；2．沈阳师范大学　教师教育学院，辽宁　沈阳　110034）

问题情境对学生建构有理数加法法则影响的差异性研究

陈丽敏1，景敏2

（1．沈阳师范大学辽宁省基础教育教研培训中心，辽宁沈阳110034；2．沈阳师范大学教师教育学院，辽宁沈阳110034）

选六年级学生为样本，比较两个版本《义务教育教科书·数学七年级（上）》中的不同问题情境对学生建构有理数加法法则的影响.结果表明：在自然数学习扩充到有理数学习的过程中，学生加法概念的迁移存在一定的困难；学生得出算式得数的正确率在两个情境中有显著性差异；学生正确列出加法算式以及得出正确答案在两个情境中没有显著性差别.

有理数加法；问题情境；认知困难

1　问题提出

在初中阶段，有理数加法是整个有理数运算的起始部分，对后续有理数减法、乘法和除法的学习起到基础性的作用，也是今后进一步学习数、式、方程等知识的基础，因此能深入理解有理数加法对于学生今后的学习至关重要.国外相关研究表明，学生在小学阶段对自然数加法意义的认识和有理数加法算理的理解不够深入，导致在中学阶段对有理数加法的理解存在认知困难[1～2]，例如，加法和乘法使结果变大，减法和除法使结果变小.国内学者对有理数运算中出现的错误以及有理数运算的理解水平展开了一些调查研究.例如，王传兵研究发现，七年级学生对“+”、“-”号的3种意义，即，表示运算符号；表示一个数是正、负数的性质符号；“-”号还可以表示相反数的理解存在一定困难[3].胡赵云研究发现，七年级学生甚至八年级学生，在学习了有理数加法法则之后仍然倾向于将有理数的加减法运算转化为自然数的加减法运算[4].巩子坤研究表明，学生对有理数运算的理解非常有限，绝大部分的学生都知道怎样算，而对于计算背后的道理知道较少[5～6].同时，一些学者的研究也表明，问题情境对于学生问题解决能力存在一定的影响.例如，张泽庆发现，和个人生活情境（如购物）相比，学生在解决社会生活情境（如工程问题）时所遇到的困难要大一些[7].戴聪以67名大学生为被试，探讨了不同的问题情境，即MHD问题的中奖情境和生存情境对被试问题解决能力的影响.结果表明：被试对MHD问题的推理成绩在生存情境下显著优于中奖情境[8].但是，问题情境对学生建构有理数加法法则影响的相关研究却很少.

鉴于此，选择人民教育出版社出版的《义务教育教科书·数学（七年级上）》（以下简称《人教版》）和北京师范大学出版社出版的《义务教育教科书·数学（七年级上）》（以下简称《北师版》）中有理数加法的导入情境来检验问题情境对学生建构有理数加法法则影响的差异.根据研究需要，研究者做了部分调整，但基本内容保持和教材中的问题情境一致.此外，选择《人教版》和《北师版》两个版本的问题情境作为研究内容也是基于本地区教师的不同认识.例如，有的教师认为《北师版》的情境更加形象，容易激发学生的兴趣，这样有利于学生建构有理数加法法则；而另外一些教师认为，《人教版》的情境和生活实际联系紧密有利于学生建构有理数加法法则等.

总体上看，建构有理数加法法则的过程分为两个阶段，第一个阶段是列出算式并根据情境得出算式的得数，第二个阶段是依据等式归纳法则.问题情境会对第一阶段产生影响，因此，研究重点关注第一个阶段.在第一阶段，问题情境对学生的影响从两个方面进行评价：一方面是学生能否根据问题情境列出正确的算式，另一方面是学生能否根据问题情境获得算式的正确得数.具体的研究假设如下：

（1）不同问题情境中，学生正确列出有理数加法的算式有显著性差异；

（2）不同问题情境中，学生正确获得算式的得数有显著性差异；

（3）不同问题情境中，学生正确得出答案有显著性差异.

2　研究过程

2.1样本的选择

选取沈阳市两所普通小学的163名六年级学生作为样本，测试时间为小学毕业前夕.选择小学六年级学生作为测试对象的原因是考虑到部分七年级学生假期可能参加了有理数加法法则的数学补习，该无关因素会对研究结果产生一定干扰.测试时间选在小学毕业前夕的原因是六年级学生已经掌握了正有理数加法、减法、乘法和除法的概念，并能解决四种混合运算的应用题，初步具备了有理数加法法则学习的知识基础.但是，学生没有学过有理数加法法则形成过程中涉及的负数和数轴概念，因此，在调查前，研究者根据初中的教学要求，对学生实施了有关负数和数轴概念的教学.

2.2问卷设计

该研究设计了两份问卷.问卷一包含两道测试题，第一道测试题选自《人教版》中的有理数加法问题情境（下文简称人教版情境）：一个物体作左右方向的运动，我们规定向左为负，向右为正.物体向右运动5米记作5 m，向左运动5米记作-5 m（在第一小问的后面提供了一个数轴的图示作为该题的认知工具）.第二道测试题选自《北师版》中的有理数加法问题情境并稍作改编（下文简称北师版情境）：某班举行知识竞赛，评分标准是：答对一题加1分，答错一题扣1分，不回答得0分.如果答对一题记作+1，用1个○+来表示，答错一题记作–1，用一个○一来表示，那么○+○一就表示0，同样○一○+也表示0（在第一小问的后面提供了相关图示作为该题的认知工具）.

问卷二的第一、二道测试题的顺序和问卷一相反.这种交叉设计方式的目的是消除两个问题情境之间的互相影响.同时，每套问卷包含《北师版》和《人教版》两个问题情境是为了消除学生能力差异对于测试结果的影响.两份问卷不仅要求学生给出正确的答案，同时也要求学生书面描述自己的思维过程，以便研究者了解学生对有理数加法意义的理解，以及得到算式得数的思维过程.

2.3评价标准

对于测试题一和测试题二的评价，可以从列式的正确率、结果的正确率、完整答案的正确率3方面进行评价.列式正确是指能够用正负数正确表示情境中的量，并选择加法运算.得数正确是指能够根据情境正确得出算式的结果.答案正确是指列式和得数都正确.

2.4测试过程

测试工作分别在两所不同发展水平的学校完成，参与测试的每个班级随机选择一半学生完成问卷一，另外一半学生完成问卷二.

3　结果描述与分析

3.1不同问题情境对学生正确列出等式影响的比较

依据问题情境列出等式是形成法则的第一步，等式包括两部分，一部分是等号一端的两个有理数之和，另一部分是基于认知工具获得的得数.北师版和人教版情境中学生列式、得数、答案正确个数的均值和标准差如表1所示（括号内数据为标准差）.

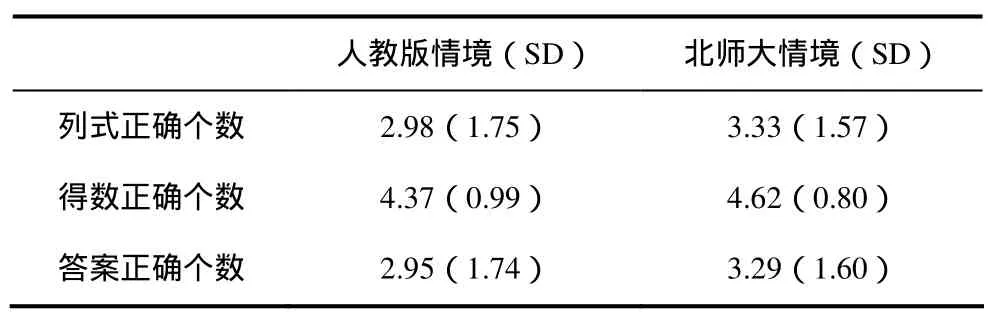
表1　两种情境学生正确个数的均值和标准差

从表1可以看出，相对于人教版情境，北师版情境在学生列式、得数、答案正确的个数方面都略胜一筹.但是，应用spss19.0统计软件的分析结果来看，在两个问题情境中，只有学生得数的正确率有显著性差异（t(324)= –2.461, P=0.01<0.05），而列式的正确率位于显著性水平的边缘值（t(324)= –1.932, P=0.054>0.05），答案的正确率无显著性的差异（t(324) = –1.827, P=0.69>0.05）.

3.2学生思维过程的描述与分析

从列式情况来看，与人教版情境相比，北师版情境更容易促进学生列出正确的加法算式（虽然二者的差别没有达到显著性的水平），产生这种差别的主要原因可能是由于不同语义的加法问题情境对学生加法意义迁移的影响是不同的.加法的语义情境有合并、变化、比较3种类型[9].合并和比较类型是静态的，变化类型是动态的.因此，北师版情境的语义是静态的，即将两个部分合并求整体是多少，而人教版情境的语义是动态的，即，两次同一方向的连续运动变化的结果.合并情境的有理数加法更容易和小学学过的加法产生联结，而变化情境的有理数加法容易和小学学过的减法产生联结.这样导致有些学生虽然能用正负数将人教版情境中相反意义的量统一，但是他们还是不知道选择加法来解决问题.

除了上述的不同之外，学生在面临两个问题情境时候，列式上也有一些相同的表现，即他们基本上都能清楚地认识到正数和负数可以表示相反意义的量，例如，对于问题“小强第一次答对3个题，第二次答错2个题，小强两次的总分是多少？”学生将答对3个题用“+3”表示，答错2题用“–2”表示，但是大部分同学直接将两个量罗列在一起，例如，“+3–2”.当要求他们解释“+3”和“–2”两个相反意义量（即，异号两数）之间的运算关系时，仅仅极少部分学生明确是加法，很大一部分学生选择了减法，剩下的学生选择了不知道.学生选择减法的理由是“答对题目个数的得分减去答错题目个数的得分是答案”.而当学生面对相同意义两个量（两数同号）之间的运算关系时，例如，对于问题“如果物体先向左运动3 m，再向左运动5 m，那么两次运动后的最后结果是什么？”大部分学生能够正确选择加法运算，并能够给出恰当的理由，即，先向左运动的数加上再向左运动的数就得到结果.

学生在有理数加法学习的过程中为什么会产生上述的认知困难呢？这个问题的产生和数学学习的本质有着紧密的联系.数学是空间形式和数量关系的科学，数学学习是一种逐步运用符号来表达现实世界的一种数学化的过程，这种过程是渐进的[10].首先，学生根据情境的信息，运用已经学习过的知识表征情境中的数学对象；接着，利用具体数学模型去表达数学对象之间的关系；之后，通过具体情境获得的方法和策略逐步概括化、一般化，并能够迁移到类似的问题情境之中；最后，通过情境获得的数学模型能够为其它形式化数学知识的获得提供土壤.在该研究中，学生有理数加法法则建构的过程也遵循上面的发展阶段.首先，学生根据问题情境提供的信息用正负数来表达情境中的数学对象；接着，学生应用加法来表达相同意义的两个量之间的关系，以及相反意义的两个量之间的关系；之后，学生进一步体会列出的有理数加法式子并深入理解有理数加法的意义，并为解决其它有理数加法问题做准备；最后，学生根据一系列有理数加法的算式抽象概括出有理数加法法则.如前文所述，该研究关注的是有理数加法法则建构的前3个阶段.从学生的表现来看，第一个阶段学生基本没有产生认知困难，往往是在第二个阶段产生了认知困难，这说明该阶段的有理数在学生的头脑中往往和情境紧密联系，并没有脱离情境像正有理数一样扎根于学生的头脑之中，这方面的不足导致部分学生即使能用正负数表示出来相反意义的量，也不清楚为什么这样做，进而不能把有理数加法和小学学过的加法产生有效联结，所以部分学生对于统一之后的两个量之间选择什么运算是很模糊的，甚至部分学生选择减法.选择减法的可能的原因是，在根据情境寻找算式答案的过程中，学生错误地认为意义相反两个量之间的抵消行为是他们之间的减法关系.

从学生算式得数的情况来看，与人教版情境相比，北师版情境中学生更容易根据正负圈之间的互相抵消得出算式的正确得数，例如，对于问题“小华第一次答错3个题，第二次答对2个题，小华两次的总分是多少？”，学生描述的思维过程为“答错3个题用3个○一表示，答对2个题用2个○+，抵消后剩一个○一，就是–1.”产生这种结果的主要原因是北师版情境和人教版情境的本质区别是两个情境的认知工具不同.北师版情境的认知工具是分散的带圆圈的正号和带圆圈的负号来表示得分和扣分，通过正负号之间的一一抵消得出结果，比较形象直观.而人教版情境是将现实的问题转化为数轴，将物体的运动转化为数轴上点的运动，向左或向右运动的距离用数轴上线段的长度来表示，通过线段之间的部分抵消得出结果，不是很形象直观.

另外，与王传兵的研究结果一致，在学生列式中也发现学生混淆了性质符号的“正号”和运算符号的“加号”，例如，对于问题“如果物体先向右运动3m，再向左运动5m，那么两次运动后的结果是什么？”学生给出算式“+3–5”的运算为减法的理由是“向右为正，向左为负，所以先加后减”.产生这种错误的主要原因追根究底还是学生没有深刻理解加法的意义.因此，在有理数加法引入之初，学生对于加号和正号，减号和负号认识产生了混淆.

4　结论与建议

对比两个情境，北师版情境在算式得数的得出方面存在一定的优越性，但是在加法算式和完整正确答案得出方面两个情境差别不大.此外，学生在两个问题情境中构建有理数的加法法则时，也存在一些相同的认知困难，即，在两个版本的问题情境中，部分学生在相反意义量的问题解决中混淆了加法运算与减法运算、运算符号和性质符号.鉴于上述认知困难，对有理数加法法则的教学给出如下建议.

首先，从研究结果可以看出，学生在六年级末，甚至七年级初，并没有真正达到将意义相反的量统一并选择正确的数学运算来解决问题的认知水平.因此，在学生自主建构有理数加法法则的第一阶段，北师版教科书在导入情境之后直接给出有理数加法的算式，只要求学生通过情境给出算式的得数，并根据有理数加法等式抽象概括得出有理数加法的法则是合理的.对于人教版教科书要求学生根据情境思考、探究有理数加法算式的处理方式，建议教师在学生列加法算式的过程中提供一些的辅助性帮助与指导.例如，在有理数加法的初始教学中，教师恰当地使用引导性问题和括号是切实可行的方法.对于人教版情境中“如果物体先向左运动3 m，再向右运动5 m，那么两次运动后的最后结果是什么？”这个问题，具体的教学方法可为，将物体同向运动的情况作为该问题的铺垫与小学阶段的加法意义取得有效联结.例如，用“如果物体先向左运动3 m，再向左运动5 m，那么两次运动后的最后结果是什么？”这个问题引导学生深入剖析为什么用加法？即，两次相同方向的连续运动是加法，以此来加深学生对加法的理解，便于后面相反方向运动的正迁移.接着，教师通过问题引导学生首先将相反意义的量表示出来，例如，物体向左运动3 m可以表示为向右运动多少米？这样做的结果可以将相反方向的运动统一为相同方向的运动.之后，教师可以引导学生先用正数和负数表示出来左运动3 m，和向右运动5 m两个量，并强调用括号将两个量分别括起来罗列在一起，即，(–3)(+5)，最后，通过和小学学过的加法取得联结，引导学生去发现这两个量之间用什么运算来连接.这种引导性问题和括号的方法可以持续1～2节课的时间，当学生能够统一相反意义的量并区分运算符号和性质符号之后，可以逐渐弱化.例如，引导性问题可以不出现，(–3)+(+5)可以表示为(–3)+5.

其次，从数学自身发展角度来看，数系从自然数扩充到有理数后，需要研究自然数的运算法则和运算律是否对有理数也成立.在自然数系中，学生熟悉数量之间的关系，即意义相同用加法，意义相反用减法.例如，问题“8月份小明基本工资收入2 000元，其它收入1 000元，8月份小明收入多少钱？”用加法解决.问题“8月份小明收入2 000元，支出1 000元，8月份小明收入多少钱？”用减法解决.当引进了有理数之后，通过正负号可以将相反意义的量统一为相同意义的量.但是由于学生对于负数的理解和加法意义的理解不深入，因此学生一旦被要求将这些正负数之间的运算关系表示出来的时候，学生又将负号表示的含义和情境中的具体信息联系起来，这样又回到了自然数减法的怪圈之中.

[1]Vamvakoussi, Van Dooren, Verschaffel. Naturally biased? In Search for Reaction Time Evidence for a Natural Number Bias in Adults [J]. Journal of Mathematical Behavior, 2012, (3): 344.

[2]Vamvakoussi, Van Dooren, Verschaffel. Educated Adults are Still Affected by Intuitions about the Effect of Arithmetical Operations: Evidence from a Reaction-Time Study [J]. Educational Studies in Mathematics, 2013, 82(2): 323.

[3]王传兵.七年级学生对负数概念的理解[D].华东师范大学，2007.

[4]胡赵云.立足学生原有认知结构重构有理数加减运算[J].数学教育学报，2004，13（4）：59.

[5]巩子坤.有理数运算的理解水平及其教与学的策略研究[D].西南大学，2006.

[6]巩子坤.基于学生的理解水平制定课程目标——以“小数乘法运算”为例[J].数学教育学报，2010，19（2）：34.

[7]张泽庆.数学问题情境对小学生解决问题能力的影响研究[D].西南大学，2011.

[8]戴聪.不同情境对于MHD问题解决的影响[J].社会心理科学，2011，（129）：1 408.

[9]Verschaffel L, De Corte E. Number and Arithmetic [A]. In: Bishop A, Clements K, Keitel C. International Handbook of Mathematics Education [C]. Dordrecht: Kluwer, 1996, (l4): 99-137.

[10] Van den Heuvel-Panhuizen M. Realistic Mathematics Education as Work in Progress [A]. In: F L Lin. Common Sense in Mathematics Education-Proceedings of 2001 the Netherlands and Taiwan Conference on Mathematics Education [C]. Taipei, Taiwan. Retrieved from: http://www.fi.uu.nl/publicaties/literatuur/4966.pdf. 2001.

Research on the Influence of Problem Contexts on Students’ Constructing the Rule of Rational Number Addition

CHEN Li-min1, JING Min2
(1. Liaoning Research and Training Center for Basic Education, Shenyang Normal University, Liaoning Shenyang 110034, China;
2. Teacher Education College, Shenyang Normal University, Liaoning Shenyang 110034, China)

163 six graders were administered two problem contexts in order to explore the influence of different problem contexts selected from two versions of seventh grade math textbooks on pupils’ constructing the rule of rational number addition. Results revealed that, first, students had cognitive difficulty in the learning of the concept of addition from natural numbers to rational numbers. Second, students’ performance on correct computational results in the two contexts was significantly different. Third, there was no significant difference between pupils’ performance on the correct mathematical operations and correct answers (i.e., computational results and mathematical operations are both correct) from the two contexts.

rational number addition; problem context; cognitive difficulty

G623.5

A

1004–9894（2015）04–0064–04

[责任编校：陈隽]

2015–07–10

辽宁省教育科学“十二五”规划2015年度课题——数学学案导学教学实施中的问题与对策研究（JG15CB006）；全国教育科学“十二五”规划2011年度教育部重点课题——校本教研与农村初中数学教研组建设案例研究（GIA117011）

陈丽敏（1976—），女，辽宁沈阳人，讲师，博士，主要从事数学教育研究．