数形结合思想在小学数学教学中的实践研究

范凌红

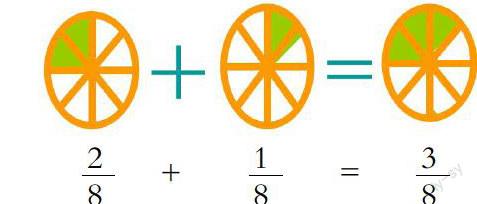
【中图分类号】G623.5 【文献标识码】A 【文章编号】2095-3089（2015）10-0138-01

数形结合思想作为一种常用的数学思想和教学方法，在小学数学中的应用有着非常重要的意义。它不仅可以加深学生对知识的理解和认识，提高学生的数学学习素养，还可以为其将来学习更加复杂的数学知识甚至终身学习打下良好的基础。但是，在我们的日常数学教学中，大部分教师仍然只是重视学生基础知识和基本技能的理解和掌握，基本上没有渗透数学基本思想的痕迹，有些教师有意渗透数学思想，却也不知从何入手。因此，在教学过程中，如何充分挖掘知识点背后的数形结合思想，教会学生使用数形结合思想解决数学问题，值得我们教师深入研究。

一、数的概念教学方面

数的产生源于对具体物体的计数，用来表示“数”的工具却是一系列的“形”。

我们不难发现从数的概念的建立到数的运算，处处蕴含着数形结合的思想方法。我们在认数以及运算时，教材基本上都是借助直观的几何图形帮助学生理解抽象的数概念。生动形象的图形不仅能将枯燥的数学知识趣味化、直观化，还能让学生从中获得“学习有趣”的情感体验，进而引导学生进行探索，将兴趣逐渐转化为动力，达到认识概念本质的目的。

例如，在教学“认识100以内的数”时，我将教材中的内容化静态为动态，通过直观图，将计数单位及相互间的“十进制”依次呈现出来（课件依次动态出示1根小棒、10根小棒变成1捆小棒、10捆小棒变成一大捆小棒）。在呈现的过程中，逐步加深学生对“1”、“10个一是1个十”、“10个十是一百”的认识，从而认识相应的计数单位 “个”、“十”、“百”，理解它们之间的十进制关系。这种形式的呈现，不仅使学生在脑海中建立了表象，还为后面数的学习打下了良好的基础，有效地实现了“数”与“形”的完美结合。

二、计算教学方面

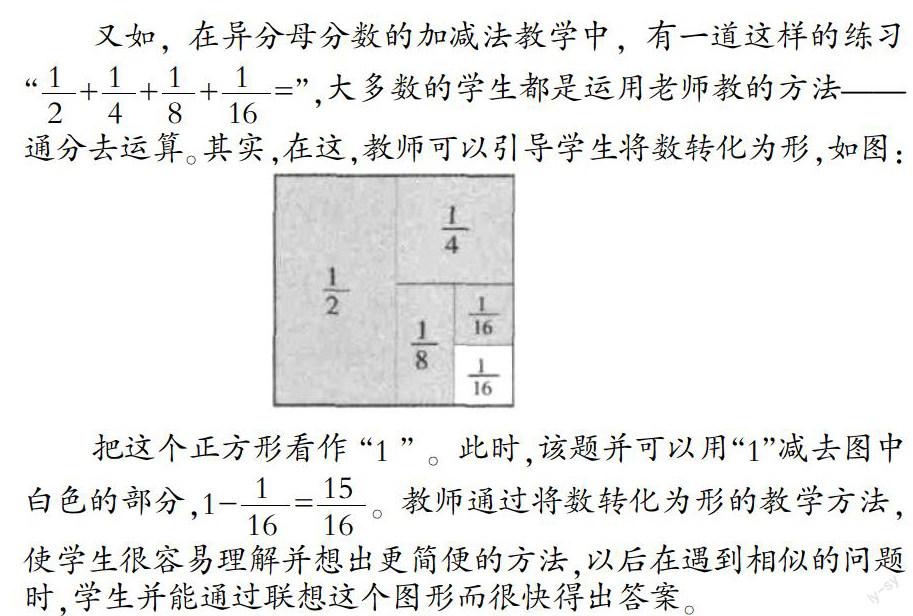
算理是数学学习的重要内容，利用“形”的生动性、直观性探索、感悟算理的形成过程，有助于对知识本质的把握。在计算教学中，许多学生对算理的理解模棱两可，如能做到数形结合，不仅可以使学生较为深刻地理解算理，还能促进学生形象思维和逻辑思维的协调发展。例如，在教学分数的加减法一课时，我们并能充分融合数形结合思想来帮助学生理解算理，如图：

整节课我们始终可以用一张圆形纸片作为素材，让学生通过“分一分、涂一涂”的操作，将“数”的问题转化为 “形”的问题，借助图形语言帮助学生理解分数加、减法的算理。这样的教学设计，既使学生充分理解了算理，又有效地突破了教学重难点，达到了良好的教学效果。

由此可见，在日常的计算教学中，教师可以充分利用“形”，把枯燥、复杂的运算变得形象、直观，丰富学生的表象，引发联想，探索规律，得到结论，不仅知其然，而且知其所以然。

三、解决问题教学方面

现在新教材中的解决问题领域的学习内容，遍布于各个章節的具体数学学习内容中，它重视数学知识和实际生活之间的联系，但是淡化了解决问题的类型，增加了学生解答的困难。因此，在教学过程中，适时采用数形结合思想，把抽象的问题解决放在直观的情境中，在直观图示的导引和教师的启发下，学生就能比较容易地理解各种数量之间的关系。例如，在苏教版一年级上册的练习中经常会出现这种类型的题目：从前往后数，小明是第5个，从后往前数，小明是第6个，一共有几个小朋友？列成算式应该是：5+6-1。但是，这道题如果让一年级孩子列式计算的话，是存在一定困难的，大部分孩子都会直接用5+6来计算。此时，教师若能采用数形结合的思想，引导孩子通过画圈来思考，很多问题并能迎刃而解。如图：

高年级教师经常会用线段图来帮助学生理解题意、分析数量关系，其实，这也是渗透数形结合思想的一种体现。在解决问题教学过程中，我们教师可以充分利用直观的“形”把抽象的问题形象化、复杂的问题简单化、明朗化，以提高学生分析比较、综合运用知识解决问题的能力。

总之，数形结合是数学教学当中一种重要的教学思想，同时也是一种有效提高小学数学课堂教学效率的重要手段。在日常教学中，教师应结合具体的内容，有意识地渗透数形结合思想，培养学生数形转化的意识。