对多元函数几类积分的理解

李　娜，王 洁

（商丘工学院基础教学部，河南　商丘　476000）

对多元函数几类积分的理解

李娜，王 洁

（商丘工学院基础教学部，河南商丘476000）

多元函数的积分是一元函数定积分在多元函数上的推广，本文把多元函数积分与一元函数定积分的概念和性质加以对比，分析两者的区别与联系，使学生从整体上更好的理解多元函数积分概念.

定积分；多元函数积分；对比

多元函数的积分是高等数学的一个重要组成部分，它是一元函数定积分在多元函数上的推广.由于多元函数的自变量个数不同，因而多元函数的积分是多样的，有二重积分、三重积分、曲线积分与曲面积分等.

1 重积分、曲线积分、曲面积分概念与定积分概念的对比

一元函数定积分定义：设函数f（x）在闭区间［a, b］上有定义.

（1）用n-1个分点a=x0＜x1＜…＜xi-1＜xi＜…xn-1＜xn=b将区间［a,b］任意分割成n个小区间［xi-1，xi］，i=1，2，…，n，小区间长为Δ xi=xi-xi-1，i= 1，2，…，n

（2）在每个小区间［xi-1，xi］上任取一点ξ1，作乘积

多元函数的常见积分形式有二重积分、三重积分、曲线积分、曲面积分，这些积分与定积分的思想方法是相同的，都是采取分割、近似代替、求和、取极限的思路.但因为函数、定义域与积分和的不同，所以有不同形式的积分.

从以上的对比中可以看出，多元函数的几类积分的思想方法与定积分是相同的，都是采取分割、近似代替、求和、取极限的思路.不同之处在于解决不同类型问题，建立不同的理论.二重积分分割的不再是某一区间，而是平面上某一有界闭区域；被积函数也不再是一元函数，而是二元函数；二重积分中出现面积元素dσ.类似的，三重积分分割的是空间内某一有界闭区域，被积函数是三元函数；三重积分中出现体积元素dv；曲线积分分割的是平面上某一光滑曲线弧；被积函数是二元函数；曲面积分分割的是空间内某一光滑曲面，被积函数是三元函数.

2 格林公式、高斯公式与牛顿-莱布尼茨公式的对比

牛顿-莱布尼茨公式

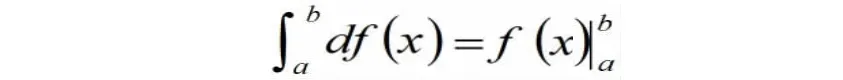
表示一元函数在区间上的定积分与它的原函数在区间边界上的值之间的联系。

类似的，格林公式

表示二重积分与曲线积分之间的关系，即一个二元函数在平面区域D上的二重积分与其“原函数”在其区域边界曲线上曲线积分之间的联系。

类似的，猜想三重积分与曲面积分的关系，高斯公式

表示一个三元函数在空间区域Ω上的三重积分与其“原函数”在其区域边界曲面上曲面积分之间的联系.

从以上比较中可以看出，利用格林公式可以把曲线积分转化为二重积分，二重积分的计算方法比较多，学生计算起来更为简单.同样，利用高斯公式可以把曲面积分转化为三重积分，三重积分的计算相对容易些，从而把复杂的积分化为相对容易些的积分.

3 重积分、曲线积分性质与定积分性质的对比

定积分、二重积分、三重积分、曲线积分都具有以下性质：

（1）积分的线性性质；

（2）积分的可加性；

（3）被积函数恒等于1时几何意义，其中

（4）积分的单调性；

（5）绝对可积性；

（6）积分估值定理:

（a）定积分估值定理：设M,m分别是f（x）在［a, b］上的最大值与最小值，则

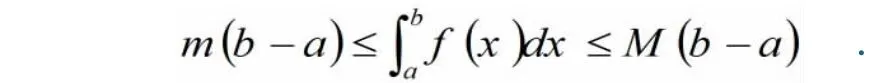
（b）二重积分的估值定理：设M,m分别是f（x,y）在闭区域D上的最大值和最小值，则

（7）积分中值定理：

（a）定积分的中值定理：设f（x）在［a,b］上连续，则存在ξ∈［a,b］，使得

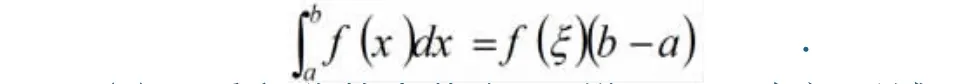
（b）二重积分的中值定理：设f（x,y）在闭区域D上连续，则在 D上至少存在（ξ，η），使得

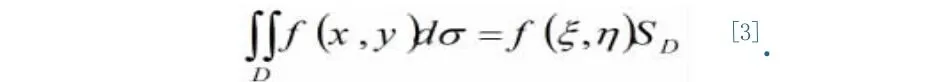
通过多元函数积分与定积分的概念和性质的对比，学生能够更好理解多元函数积分概念，同时掌握多元函数积分的计算及其相互转化.

［1］龚德恩，范培华.微积分［M］.第2版.北京：高等教育出版社，2008:187-188.

［2］同济大学数学系.高等数学［M］.第6版.北京：高等教育出版社，2007134-215.

［3］马建珍.论《数学分析》课程的整合［J］.邢台学院学报，2013（2）:160-161.

U nderst andi ngof Mult i pl e Funct i ons for Several Types of Int egral

LINa，WANGJie
（BasicTeachingDepartment，ShangqiuInstituteofTechnology，ShangqiuHenan476000）

Integrationofmultivariatefunctionisageneralizationofabinaryfunctionofdefinite integral in the function of many variables.In this paper，the concept and nature of multi-function integration is compared with the functions of one variable definite integral，both the differences and connections are analyzed.As a result，students can better understand the whole concept of multi-functionintegral.

DefiniteIntegral；MultivariateFunctionIntegration；Contrast

O 172.2

A

1672-2094（2015）01-0152-02

责任编辑：张隆辉

2014-11-24

李娜（1984-），女，河南商丘人，商丘工学院基础教学部助教，硕士。研究方向：微分方程数值解。