力—电模拟法分析受迫振动

王长江

（四川职业技术学院电子电气工程系，四川 遂宁　629000）

力—电模拟法分析受迫振动

王长江

（四川职业技术学院电子电气工程系，四川 遂宁629000）

基于力—电模拟，用电路知识讨论力学系统中受迫振动的性质及其共振规律.

力—电模拟；受迫振动；共振规律

机械振动系统如图1所示，图中，k为弹簧倔强系数，m为物体质量.物体所受外力Fmcos（ωt），阻尼力（式中，b为阻尼系数），则物体的运动方程为

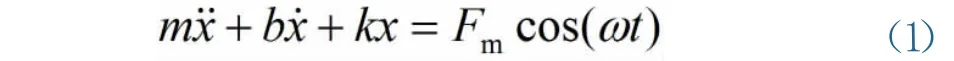
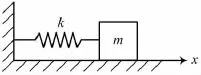
图1 机械振动系统

对于机械系统振动规律的研究，传统方法是通过分析二阶常系数线性非齐次微分方程的解来解决，本文给出另一种研究方法，即力—电模拟法.

1 力—电模拟

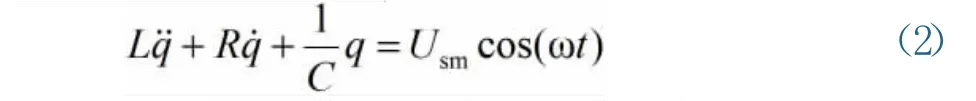
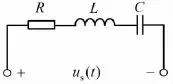
图2 RLC串联电路

从方程（1）和（2）可以看出，方程中对应变量和系数所代表的物理性质具有相似性，因而，在图1所示的机械振动系统与图2所示的RLC串联电路之间，能够建立起如下力—电模拟：

力Fm～电压Usm质量m～电感L

弹性系数k～倒电容1/C阻尼系数b～电阻R

对于具有耗散力的力学系统，拉格朗日方程为

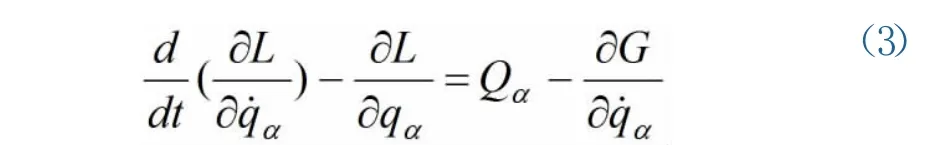
在图2所示电路中，取广义坐标qa为电荷q，广义速度为电流，广义力为端电压us，不难得到

将它们代人拉格朗日方程（3），不难得到电路方程（2）.由此分析可知，图2可以作为图1的模拟电路.

2 共振特性

根据力—电模拟，由电路知识可得到，表征力学系统振动的全部过程的两个参量：

3 共振规律

3.1 速度共振

RLC串联电路中，电流幅值为根据力-电模拟，则受迫振动系统的速度振幅为

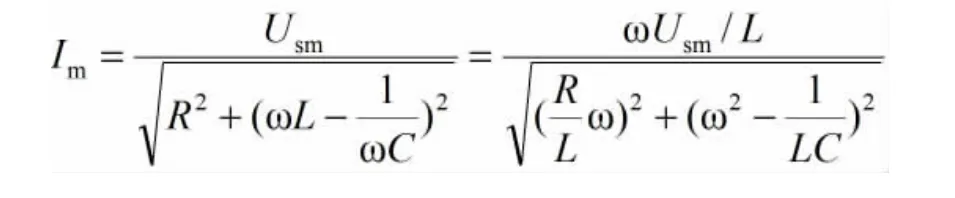
3.2 位移共振

RLC串联电路中，电容电压幅值与电路中电流幅值的关系为

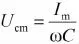
电容上电荷的振幅值为

将Im代入上式可得

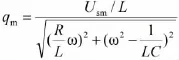
根据力—电模拟，受迫振动系统的位移振幅为

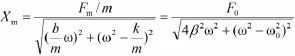
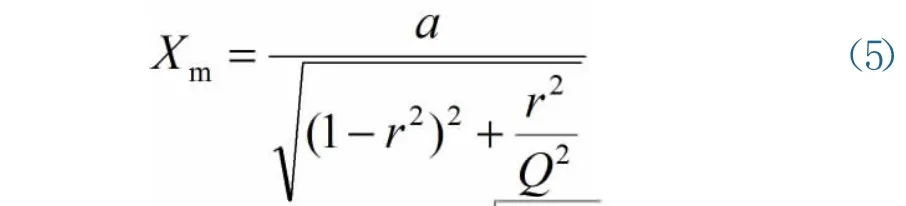
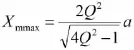
3.3 加速度振幅

电感电压幅值与电路中电流幅值的关系为

将Im代入上式可得

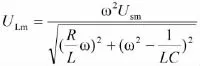
根据力—电模拟，受迫振动系统的加速度振幅为

［1］王长江﹒拉格朗日方程在电路中的应用［J］﹒四川职业技术学院学报，2013（5）：163-164﹒

［2］周衍柏﹒理论力学教程［M］﹒第2版.北京：高等教育出版社，2004﹒

［3］俎云霄﹒电路分析基础［M］﹒北京：电子工业出版社，2004﹒

Force-el ect ri c Si m ul at i onA nal yses of ForcedV i brat i on

WANGChangjiang
（SichuanVocationalandTechnicalcollege，Suining sichuan 629000）

Based on force-electric simulation，the nature and the resonance laws of forced vibrationofamechanicalsystemarediscussedonthecircuitknowledge﹒

es：Force-electricSimulation；ForcedVibration；LawofResonance

TM 13

A

1672-2094（2015）01-0157-02

责任编辑：张隆辉

2014-09-26

王长江（1965-），男，四川渠县人，四川职业技术学院电子电气工程系副教授。