关于反射等价关系的变换半群的注记

孙俊岭，孙垒

（河南理工大学数学与信息科学学院，河南焦作454003）

关于反射等价关系的变换半群的注记

孙俊岭，孙垒

（河南理工大学数学与信息科学学院，河南焦作454003）

设TX是非空集合X上全变换半群，E是X上非平凡的等价关系，则T∃（X）是TX的子半群.在赋予半群T∃（X）自然偏序关系的条件下，本文刻画了它的相容元.

变换半群；自然偏序关系；相容元

1　引言

文献［1］在任意半群S上定义了如下偏序关系≤.

定理1.1设≤是半群S上偏序关系，a，b∈S，则下面命题等价.

（i）a≤b；

（ii）a=wb=bz，az=a，=其中w，z∈S1；

（iii）a=xb=by，xa=ay=a，其中x，y∈S1.

这种偏序关系，称为自然偏序关系.对于变换半群自然偏序关系的研究，参见文献［2-5］.设TX是非空集合X（|X|≥3）上全变换半群，E是X上等价关系.文献［6］最早引入了TX的反射等价关系的子半群

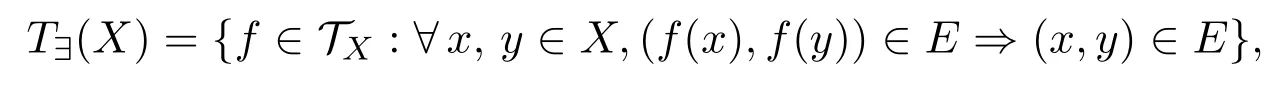
刻画了它的格林等价关系L，R，H，D，J和正则元.文献［7］赋予变换半群T∃（X）自然偏序关系≤，即f，g∈T∃（X），

其中，h，k∈T∃（X），刻画了它的特征，得到了如下结论.

定理1.2［7］设f，g∈T∃（X），则f≤g当且仅当下面条件同时成立.

（1）π（g）加细π（f）且|Z（g）|≤|Z（f）|；

（2）若（f（x），f（y））∈E（其中x，y∈X），则（g（x），g（y））∈E；

（3）若g（x）∈f（X）（其中x∈X），则f（x）=g（x）；

（4）对于任意A∈Ω（E），有f（A）⊆g（A）.

设f，g，h∈T∃（X）.若对于任意f＜g（f≤g），有hf＜hg（hf≤hg），则h称为严格左相容的（左相容的）.对偶的，若对于任意f＜g（f≤g），有fh＜gh（fh≤gh），则h称为严格右相容的（右相容的）.

定理1.3［7］设h∈T∃（X），则下面命题成立.

（1）h是严格左相容当且仅当h是集合X上单射，且对于任意A∈Ω（E），有h（A）⊆B∈Ω（E）.

（2）h是严格右相容当且仅当h是集合X上满射.

本文在赋予半群T∃（X）自然偏序关系的条件下，刻画它的左相容元和右相容元，给出充要条件.下面介绍本文中的概念和符号.π（f）表示由f∈TX确定的X的分类，即

令X为集合，E为X上等价关系.用Ω（E）表示由E确定的X的相应分类.设A，B是集合X的两个子集族，若对于任意A∈A，存在B∈B，使A⊆B，则称子集族A加细子集族B.记

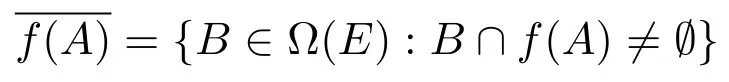
且

h|A表示映射h在集合A上的限制.本文中等价关系E是非平凡的，即

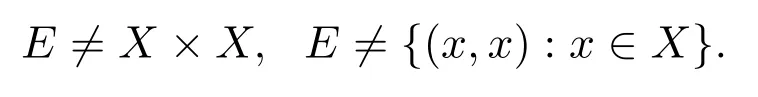
2　主要结论

定理2.1设h∈T∃（X），则h是左相容元当且仅当对于任意E-类A，h|A是单射且h（A）⊆B∈Ω（E），或者h|A是常值映射.

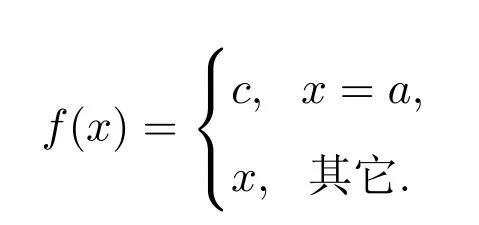
证明（1）必要性.设h是左相容元.现在用反证法证明对于任意E-类A，h|A是单射或者h|A是常值映射.若不然，则存在E-类A∗，满足h|A∗既不是单射又不是常值映射.设h（a）=h（b）≠h（c），其中a，b，c∈A∗.如下定义映射f：X→X显然f∈T∃（X）且f≤idX，其中idX是集合X上恒等映射.于是hf≤hidX=h.由定理1.2条件（1）知π（h）加细π（hf）.但是，一方面h（a）=h（b）；另一方面，hf（a）=h（c），hf（b）=h（b）.由h（c）≠h（b）知hf（a）≠hf（b）.这与π（h）加细π（hf）矛盾.因此对于任意E-类A，h|A是单射或者h|A是常值映射.下面证明对于任意A∈Ω（E），若h|A是单射，则h（A）⊆B∈Ω（E）.不失一般性，设其中A∗，B1，B2∈Ω（E）.记A∗1=｛x∈A∗：h（x）∈B1｝且A∗2=｛x∈A∗：h（x）∈B2｝，则A∗=A∗1∪A∗2且A∗1∩A∗2=∅.取定x′∈A∗1.如下定义映射k：X→X

显然k∈T∃（X）且k≤idX.于是hk≤hidX=h.现取定y′∈A∗2，则一方面有（hk（x′），hk（y′））∈E，另一方面有h（x′）∈B1，h（y′）∈B2.这表明（hk（x′），hk（y′））∈E不蕴含（h（x′），h（y′））∈E.这与定理1.2条件（2）矛盾.从而，若h|A是单射，则对于任意A∈Ω（E），有h（A）⊆B.故必要性成立.

（2）充分性.设h满足假设条件即对于任意E-类A，h|A是单射且h（A）⊆B∈Ω（E），或者h|A是常值映射.对于任意f，g∈T∃（X）且f≤g，下面分别验证hf，hg满足定理1.2条件（1）-条件（4）.

（1）令hg（x）=hg（y），其中x，y∈X.由h∈T∃（X）知，（g（x），g（y））∈E，即

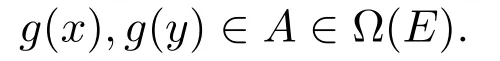
若g（x）=g（y），则由f≤g和定理1.2条件（1）知，f（x）=f（y）.于是hf（x）=hf（y）.若g（x）≠g（y），此时h|A是常值映射.记f（x）=g（x′），其中x′∈X.由定理1.2（3）知f（x′）=g（x′）=f（x）.于是（f（x），f（x′））∈E.由定理1.2条件（2）知（g（x），g（x′））∈E.根据g（x）∈A，有g（x′）∈A，即f（x）∈A.同理f（y）∈A.于是hf（x）=hf（y）.这表明π（hg）加细π（hf）.由|Z（g）|≤|Z（f）|知因此进而|Z（hg）|≤|Z（hf）|.这表明hf，hg满足定理1.2条件（1）.

（2）令（hf（x），hf（y））∈E，其中x，y∈X，则（f（x），f（y））∈E.由f≤g知（g（x），g（y））∈E.注意到h在每个E-类上不管是单射还是常值映射，都将每个E-类映入一个E-类中.于是（hg（x），hg（y））∈E.这表明hf，hg满足定理1.2条件（2）.

（3）设hg（x）∈hf（X），即hg（x）=hf（x′），其中x′∈X.若g（x）=f（x′），则由定理1.2条件（3）知f（x）=g（x）.因此hf（x）=hg（x）.若g（x）≠f（x′），此时h在g（x），f（x′）所在的E-类上是常值映射.由定理1.2（4）知存在y∈X，使f（x）=g（y）.根据定理1.2条件（3），有f（y）=g（y），即f（x）=g（y）=f（y）.进而（f（x），f（y））∈E.由定理1.2条件（2）知（g（x），g（y））∈E，即（g（x），f（x））∈E.因此hf（x）=hg（x）.这表明hf，hg满足定理1.2条件（3）.

（4）显然hf，hg满足定理1.2条件（4）.因此hf≤hg.故h是左相容元.

定理2.2设h∈T∃（X），则h是右相容元当且仅当h是满射.

证明参照文献［7］的定理3.3的证明.

［1］Mitsch H.A natural partial order for semigroups［J］.Proceedings of the American Mathematical Society，1986，97（3）：384-388.

［2］Kowol G，Mitsch H.Naturally ordered transformation semigroups［J］.Monatshefte Fur Mathematik，1986，102（2）：115-138.

［3］Marques-Smith M Paula O，Sullivan R P.Partial orders on transformation semigroups［J］.Monatshefte Fur Mathematik，2003，140（2）：103-118.

［4］Sullivan R P.Partial orders on linear transformation semigroups［J］.Proceedings of the Royal Society Edinburgh Section A-Mathematics，2005，135（2）：413-437.

［5］Sun L，Deng W N，Pei H S.Naturally ordered transformation semigroups preserving an equivalence and a cross-section［J］.Algebra Colloquium，2011，18（3）：523-532.

［6］Deng L Z，Zeng J W，You T J.Green′s relations and regularity for semigroups of transformations that preserve reverse direction equivalence［J］.Semigroup Forum，2011，83（3）：489-498.

［7］Sun L，Xin X J.The natural partial order on the semigroup of all transformations of a set that reflect on equivalence relation［J］.Bullet of the Australian Mathematical Society，2013，88（3）：359-368.

A note on naturally ordered semigroups of transformations of a set that reflect an equivalence relation

Sun Junling，Sun Lei

（School of Mathematics and Information Science，Henan Polytechnic University，Jiaozuo454003，China）

Let TXbe the full transformation semigroup on a nonempty set X and E be a nontrivial equivalence relation on X，then T∃（X）is a subsemigroup of TX.In this paper，we describe all the left and right compatible elements in the transformation semigroup T∃（X）endowed with the natural partial order.

transformation semigroup，natural partial order，compatible element

O152.7

A

1008-5513（2015）05-0464-04

10.3969/j.issn.1008-5513.2015.05.004

2015-04-12.

国家自然科学基金（U1404101）；河南省教育厅科学技术研究重点项目基础研究计划（14A110003）.

孙俊岭（1979-），硕士，讲师，研究方向：代数学.

2010 MSC:20M20