带周期位势平面薛定谔-泊松方程组的结点解
郭文艳,章国庆,刘三阳
(1.上海理工大学理学院,上海200093;2.西安电子科技大学数学和统计学院,陕西西安710071)
带周期位势平面薛定谔-泊松方程组的结点解
郭文艳1,章国庆1,刘三阳2
(1.上海理工大学理学院,上海200093;2.西安电子科技大学数学和统计学院,陕西西安710071)
利用临界点理论中的亏格定理和Nehari流形技巧,本文证明了在二维全空间上一类带周期位势的薛定谔-泊松方程组高能量解的存在性,且该解存在无穷多个结点区域.更进一步,得到了其基态解的存在性且是不变号的.
平面薛定谔-泊松方程组;周期位势;结点解
1 引言
本文考虑如下带周期位势的平面薛定谔-泊松方程组:
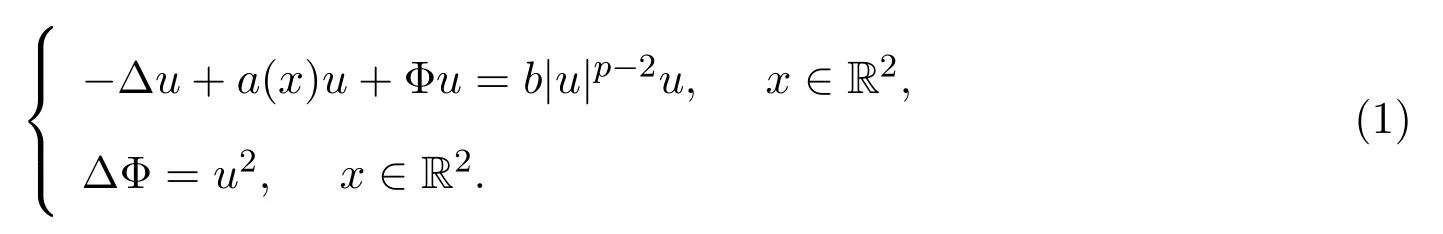
其中b<0,2<p<4,函数a(x)满足条件:
(A)a:R2→(0,∞)为Z2周期连续函数,a(x)∈L∞(R2)且
因薛定谔-泊松方程组来源于量子力学和半导体理论,研究它的解的存在性是一个具有物理意义的问题.近年来,许多学者进行了广泛地讨论.对于在三维全空间上的薛定谔-泊松方程组,当b=0时,文献[1-2]证明了基态解的存在性、多重性以及对称性.当b>0,2<p<6时,文献[3]得到了解的存在性.当b<0时,此时薛定谔-泊松方程组描述了液晶中的Hartree模型,文献[4]讨论了,当时,存在无穷多个径向解.对于在二维全空间上的薛定谔-泊松方程组的研究,现有文献并不多见.文献[5]利用打靶法,证明了解的存在唯一性;特别是,2014年,文献[6]利用变分法得到了,当b>0,p≥4时,问题(1)解的存在性与对称性.
本文讨论在b<0,2<p<4时,问题(1)高能量解的存在性与变号性(即:其解存在无穷多个结点区域),并进一步证明了其基态解的存在性与不变号性.当b<0时,此时在物理学上表示物质具有“正能量”,研究其解是一个有意义的课题.此外,因为函数a(x)为Z2周期函数,需要更精细的估计来得到其对应的能量泛函满足Cerami条件(紧性条件);利用Nehari流形技巧时,因为b<0,此时需要分析对应能量泛函的性态(如:单调性等).另一方面,因为问题(1)的第二个方程的Green函数是变号的,这为利用变分法研究带来困难.
2 预备知识和主要结论


本文的主要工具是亏格定理和Nehari流形,下面给出本文所需要的一些预备知识和引理.
定义2.1[9]设D⊂Y是X的闭对称子集,定义Y相对于D的亏格γD(Y),如果存在k,使得Y能被闭对称子集U,V覆盖,且满足下列性质:
(1)D⊂U且存在奇连续映射χ:U→D使得χ(u)=u,u∈D;
(2)γ(V)≤k.
若不存在上述覆盖,则定义γD(Y)=∞.
引理2.2[9]设D,Y,Z是X的闭对称子集,且D⊂Y,则
(1)(次可加性)γD(Y∪Z)≤γD(Y)+γ(Z);
(2)若D⊂Z,且存在奇连续映射φ:Y→Z使得φ(u)=u,u∈D,则γD(Y)≤γD(Z).
定义2.3[10]称集合

为泛函I的Nehari流形.如果u≠0为泛函I(u)的临界点并且满足则称u为I的最小能量临界点(即:问题(1)的基态解).
定理2.4假设b<0,2<p<4,且a(x)满足条件(A),则问题(1)存在高能量解(u,Φ),且u有无穷多个结点区域,即,存在结点解序列{±un}∈X,使得I(un)→∞(n→∞).
定理2.5假设b<0,2<p<4,且a(x)满足条件(A),则问题(1)存在基态解,且基态解是不变号的.
3 Cerami条件
为了利用亏格定理和Nehari流形技巧,首先要证明Cerami条件(紧性条件)成立.因为函数a(x)满足条件(A),故泛函I在Z2变换下是不变的.对于函数u:R2→R,x∈R2,定义
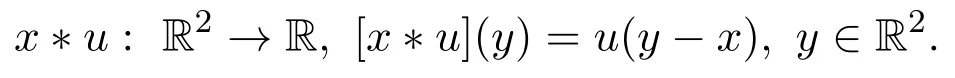
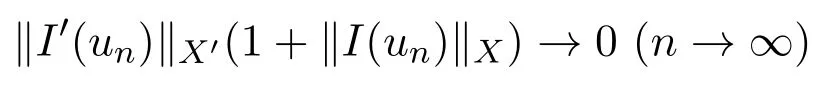
定理3.1设{un}是X中的Cerami序列,即I(un)→d>0,,则存在子列{un},点列{xn}∈Z2,n∈N,使得在X中,有xn∗un→u(n→∞).
引理3.2若{tn}是[0,∞)中的有界序列,则I(tnun)≤I(un)+o(1)(n→∞).此外,若tn→0(n→∞),则

定理3.1的证明




4 主要定理的证明
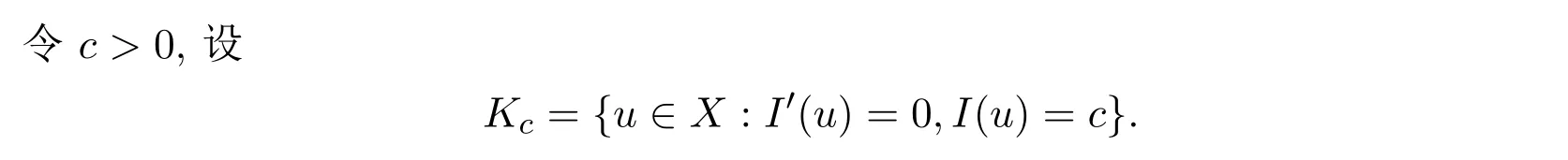

断言1ck为泛函I的临界值.事实上,假设存在k,使得Kck=∅,则对每个ρ>0,有Ac,ρ=∅.由文献[6]中,引理4.6知,存在ε>0及奇连续映射η:Ick+ε→Ick-ε,使得η|D=id|D.这与ck定义矛盾.
断言2当k→∞时,有ck→∞.事实上,假设当k→∞时,有ck→c<∞.则由形变引理及(7)知,存在ρ,ε>0,使得γ(Ac,ρ)<∞,Ac,ρ∩D=∅,并存在奇连续映射φ:Ic+εAc,ρ→Ic-ε满足φ|D=id|D.因此,由c的定义知γD(Ic+εAc,ρ)≤γD(Ic-ε)<∞.此外,由引理2.2知,γD(Ic+ε)≤γD(Ic+εAc,ρ)+γ(Ac,ρ)<∞.这与对所有的k∈N,有c+ε>ck矛盾.
综合断言1和断言2可得,存在结点解序列{±uk}∈X,k∈N,使得

引理4.1存在α>0,使得
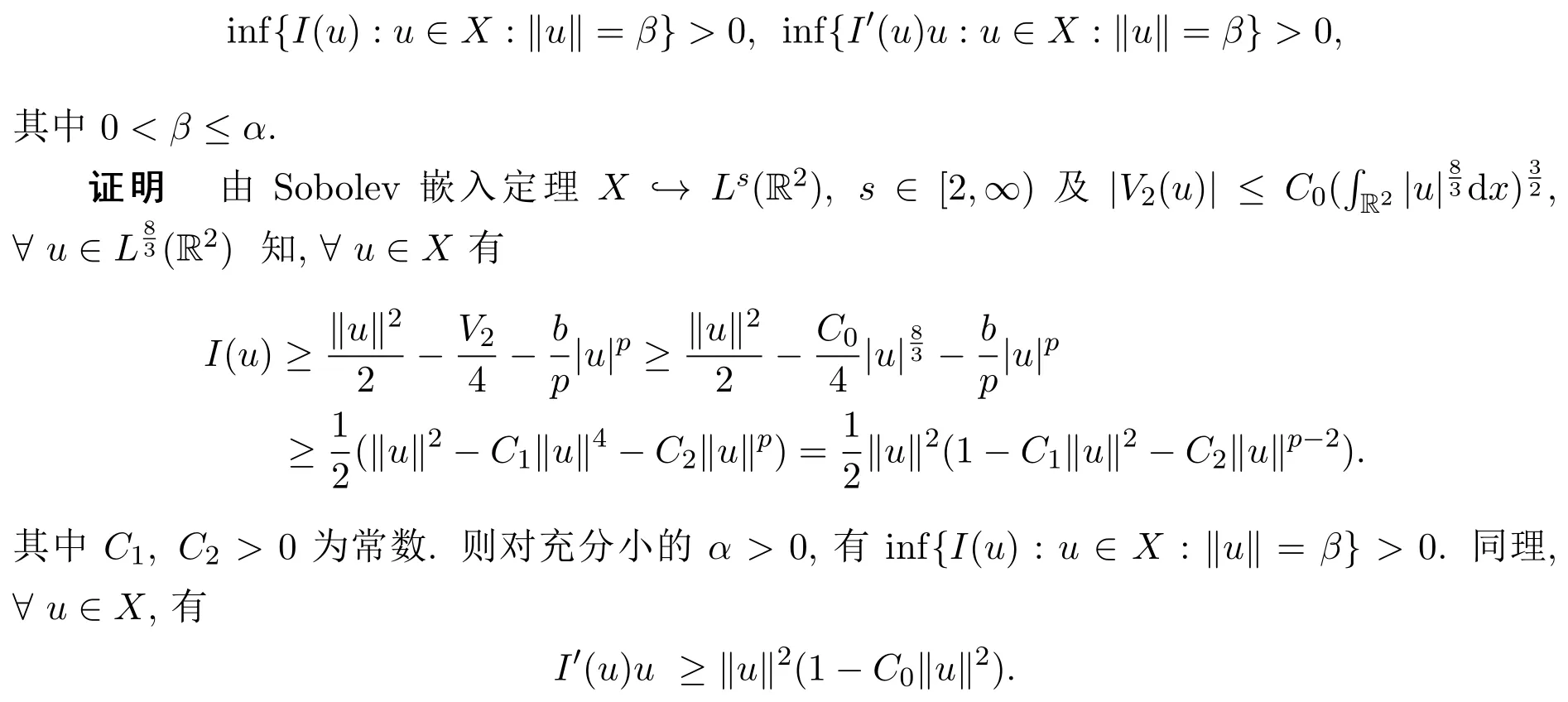
则对充分小的α>0,有inf{I′(u)u:u∈X:‖u‖=β}>0.
引理4.2设u∈X{0},则函数φu:R→R,φu(t)=I(tu)为偶函数,且满足下列性质

定理2.5的证明断言

[1]Lieb E H.Existence and uniqueness of the minimizing solution of Choquard's nonlinear equation[J].Stud.Appl.Math.,1977,57:93-105.
[2]Lions P L.Solutions of Hartree-Fock equations for Coulomb systems[J].Commun.Math.Phys.,1984,109:33-97.
[3]Ambrosetti A.On Schrödinger-Poisson systems[J].Milan Journal of Mathematics,2008,76:257-274.
[4]Mugnai D.The Schrödinger-Poisson system with positive potential[J].Commun.Partial Differ.Equ.,2013,36:1009-1117.
[5]Choquard P,Stubbe J,Vuffray M.Stationary solutions of the Schrödinger-Newton model-an ODE approach[J].Differ.Integral Equ.,2008,21:665-679.
[6]Cingolani S,Weth T.On the planar Schrödinger-Poisson system[J].Ann.I.H.Poincare-AN(2014).
[7]Lieb E H.Sharp constants in the Hardy-Littlewood-Sobolev and related inequalities[J].Ann.of Math.,1983,118:349-374.
[8]J.Stubbe,Bound states of two-dimensional Schrödinger-Newton equation[J].ArXiv:0807.4059,2008.
[9]Clapp M,Puppe D.Critical point theory with symmetries[J].J.Reine Angew.Math.,1991,418:1-29.
[10]Willem M.Minimax Theorems[M].//Progress in Nonlinear Differential Equations and Their Applications,Vol.24.Birkhäuser:Boston,1996.
Nodal solutions for a class of planar Schrödinger-Poisson systems with periodic potential
Guo Wenyan1,Zhang Guoqing1,Liu Sanyang2
(1.College of Sciences,University of Shanghai for Science and Technology,Shanghai200093,China;2.College of Mathematics and Statistics,Xidian University,Xi′an710071,China)
In this paper,using genus theorem and Nehari manifold techniques in critical points theory,we prove the existence of high energy solutions for a class of Schrödinger-Poisson systems with periodic potential in dimension two,and obtain that the solution has infinitely nodal domains.Furthermore,the existence of ground state solution is proved which does not change sign.
Planar Schrödinger-Poisson systems,periodic potential,nodal solutions
O175.25
A
1008-5513(2015)05-0542-09
10.3969/j.issn.1008-5513.2015.05.016
2015-04-07.
上海市自然科学基金(15ZR1429500);沪江基金(B14005);上海理工大学培育基金(15HJPYMS03).
郭文艳(1991-),硕士生,研究方向:非线性泛函分析.
2010 MSC:35J60,35J65

