关于四元二次型表整数个数的均值估计

王丹，劳会学

（山东师范大学数学科学学院，山东济南250014）

关于四元二次型表整数个数的均值估计

王丹，劳会学

（山东师范大学数学科学学院，山东济南250014）

利用数论函数的可乘性和狄里克雷卷积方法，研究了用四元二次型表整数个数的均值估计，并且得到了相应的渐近公式，推广了相关结果.

渐近公式；可乘函数；卷积方法

1　引言

设rk（n）表示一个整数n分解成k个整数的平方的个数，文献［1］考虑了有关整点在圆锥体

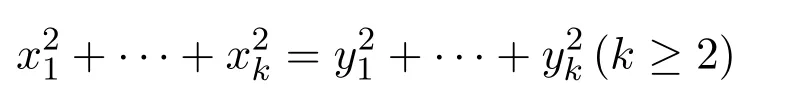
上的分布，得到了如下渐近公式

其中，c=c（k）＞0是一个确定的常数.当k=4时，Fomenko进一步改进结果为：

设f是一个定义在环O上的二元Hermitian形式，其中这个环是虚二次域（判别式D＜0）的整环，而g是相应的整数集Z上的四元二次型.文献［2］用

来表示整数n的表示个数.

本文研究了f（c，d）=2|c|2+|d|2，g（x，y，u，v）=2（x2+xy+3y2）+u2+uv+3v2时，整数n的表示个数

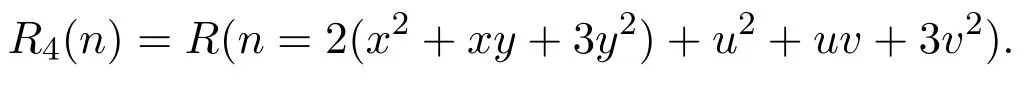
具体地得到了下面的渐近公式.

定理1.1当x≥2时，

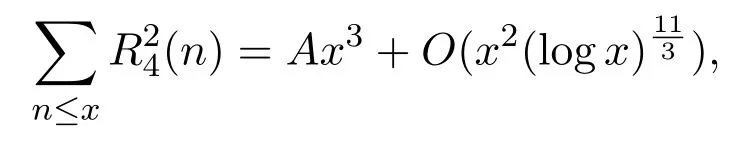
其中A是一个常数.

2　引理

为了证明定理1.1，需要下面的四个引理：

引理2.1［2］

引理2.2［3］当时，有

引理2.3［4］当x≥2时，有

其中w（m）表示m的不同素因子的个数.

引理2.4［4］

3　定理1.1的证明

［1］Fomenko O M.On the distribution of integral points on cones［J］.Journal of Mathematical Sciences，2011，178：227-233.

［2］Elstrodt J，Grunewald F，Mennicke J.Zeta-functions of binary Hermitian forms and special values of Eisenstein series on three-dimensional hyperbolic space［J］.Math.Ann.，1987，277：655-708.

［3］Titchmarsh E C.The Theory of the Riemann Zeta-Function［M］.New York：Clarendon Press，1986.

［4］Ramaiah V Sita，Suryanarayana D.An order result involving the σ-function［J］.Indian J.pure appl.Math.，1981，12（10）：1192-1200.

［5］潘承洞.数论基础［M］.北京：高等教育出版社，2012.

［6］卡拉楚巴.解析数论基础［M］.2版.潘承洞，张南岳，译.哈尔滨：哈尔滨工业大学出版社，2014.

The mean value on numbers of representation of integers by quaternary quadratic forms

Wang Dan，Lao Huixue
（School of Mathematical Sciences，Shandong Normal University，Jinan250014，China）

Using the multiplicative property of number theory function and Dirichlet's convolution method，this paper studies the mean value of the number of representations of integers by quaternary quadratic forms，and establishes an asymptotic formula，which generalizes the related result.

asymptotic formula，multiplicative function，convolution method

O156.4

A

1008-5513（2015）05-0525-08

10.3969/j.issn.1008-5513.2015.05.013

2015-04-24.

国家自然科学基金（11111049）.

王丹（1989-），硕士生，研究方向：解析数论.

2010 MSC:11P21，11E25