最优经济增长下劳动密集度的变动规律
□徐跃华朱殊洋
(21、广州大学马克思主义学院,广东广州510006;2、中共广州市委党校经济学教研部,广东广州510070)
最优经济增长下劳动密集度的变动规律
□徐跃华1朱殊洋
(21、广州大学马克思主义学院,广东广州510006;2、中共广州市委党校经济学教研部,广东广州510070)
经济学界一直将高劳动密集度看做是高速经济增长的促进因素。但劳动密集度相对于最优经济增长是否存在切换点?如果存在切换点,那么切换的条件是什么?本文通过分析最优经济增长下劳动密集度的变动规律,研究发现:在经济增长率实现最优的情况下,最优劳动密集度是存在的,而且是稳定的;在经济增长率实现最优的情况下,劳动密集度的时间轨线是一条饱和曲线,试图采用提高劳动密集度来增加就业之方法并不总是可行的;提高分工程度是保证高经济增长与高就业同步的根本方法。
最优经济增长;劳动密集度;变动规律
改革开放以来,我国经济学界一直将我国的高劳动密集度看做是高速经济增长的促进因素。这一观点在很长一段时间内影响着国家经济政策的走向,并成为相关意识形态的主流。其逻辑是,作为人口大国,我们的劳动力过剩,因而有大量的人口红利;因此我们就应该大力发展劳动密集度高的产业,发挥我国的比较优势,充分利用人口红利,这样才能够促进经济的高速增长。可以概括为如下命题:人口多→高劳动密集度→高人口红利→高速经济增长。
从我国改革开放的实践看,这一理论确实起到过积极的作用。但这一命题也存在诸多令人困惑的问题,比如这一命题链条中有三个推理逻辑,这三个推理过程是无条件成立吗?如果是有条件的,那么这一条件是什么?劳动密集度相对于最优经济增长是否存在切换点?如果存在切换点,那么切换的条件是什么?上述问题归结起来就是在最优经济增长下的劳动密集度的运动规律问题。本文试图通过数理建模来考察上述问题。
一、经济增长与劳动密集度关系的建立
由于劳动密集度与经济增长率的关系具有直接性,因而只涉及生产过程和劳动力市场关系,因此本研究的基础就是生产函数和劳动力供求函数。
(一)假设与定义
1.生产函数。本文采用文献[1]推导出的马克思的生产函数,即
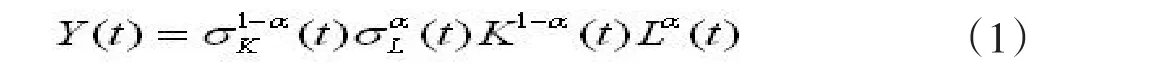
式中Y(t)为在t年实际新增价值,即实际GDP。K(t)为在t年实际资本存量,L(t)为在t年实际就业量,α为活劳动对产出的贡献,1-α为物化劳动对产出的贡献。бL(t)为在t年平均每一劳动力所包含的活劳动数量,бk(t)为在t年平均每一资本所包含的物化劳动数量。活劳动效率增长率和物化劳动效率的增长率表示为бL'/бL和бK'/бK,前者反映的是劳动者素质、后者反映生产资料质量,两者反映的是技术进步,令其为常数。因为(1)式中的时间为同期时间,所以为了方便,(1)式去掉时间标志得

2.劳动密度。定义就业数量与资本之比为劳动密度,即

这是反映资本吸纳就业的能力的重要指标。
3.劳动力供求函数。本文采用经济学文献普遍采用劳动力供给函数,即

其中n为人口自然增长率,N为就业最大允许空间。对于劳动需求,一般经济学中设为实际工资的函数。但是在我国实际工资已经很低因而工资调节能力有限,为此我们将劳动力需求量定义为劳动力最大允许空间N,它是资本数量的函数,投资增加因而资本存量扩大则会引起就业允许空间的扩大,进而导致就业量的增加。因此可以设定N=K/b,其中b是一个反映资本稀缺程度的指标。将N=K/b代入(4)式即可得到L'(t)=nL[1-b(L/K)]。
4.文中各个函数均为连续可微的。
(二)模型
对生产函数(2)进行变形得
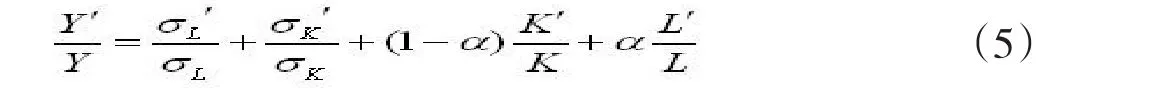
由劳动密度定义(3)可得
z'/z=L'/L-K'/K(6)将(6)代入(5)式并化简得
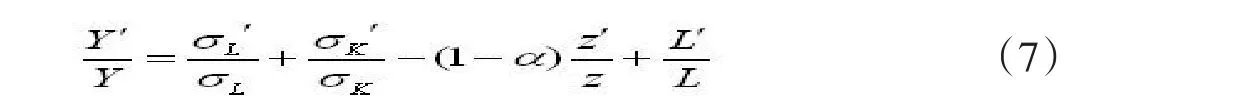
再将(3)式代入劳动力函数(4)得将(8)式代入(7)式得

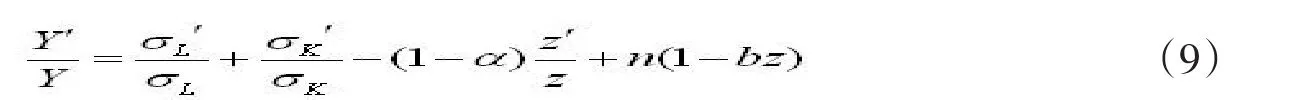
式
(9)就是经济增长率与劳动密集度关系模型。
二、最优经济增长下的劳动密集度运动规律
对(9)式求导得

为了求得经济增长率最优条件下的劳动密集度,令(Y'/Y)'=0,则

式
(11)是一个比较复杂的二阶非线性微分方程。设z'=p,代入(11)式得由
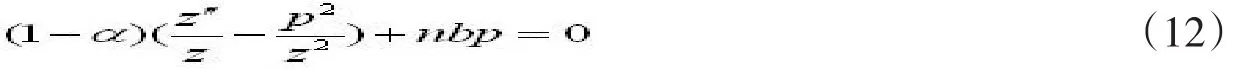
,将其代入(12)式得

由题意可知p≠0,所以(13)式为

上式变形为

令p/z=u,即p=uz,则p'(z)=u'(z)z+u,将其代入上式得

化简为

对上式积分得

将p/z=u代入上式得

其中C0为第一个积分常数。将z'=p代入上式得

对于方程(20),采用变量替换法。设v=z-1,对其求导

将(20)式代入(21)得

对上式积分得

其中c1是积分常数。将v=z-1代入上式得

这里z*表示的是在经济增长率最优条件下的劳动密集度,因而式(24)就是最优劳动密集度的变化规律。最优劳动密集度可由(24)来确定,因此(24)就是保持最优经济增长所需要的最优劳动密集度条件,换句话说就是,只有满足这一条件,经济增长率才能够实现最优。
由(24)可知,如果实际劳动密集度,则实际劳动密集度与最优经济增长率同方向变化;如果实际劳动密集度z(t)大于z*(t),则实际劳动密集度与最优经济增长率反方向变化。
三、劳动密集度分析
(一)劳动密集度的影响因素
对于(21)式和(24)式,为了简单,取t=t0=0,得
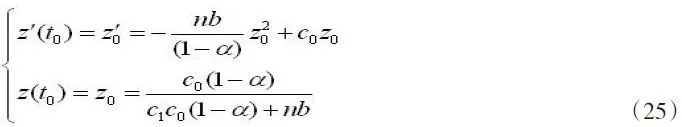
其中z'0和z0为初始已知条件。由(25)第一式得

其中z'0/z0=β。由(25)第二式得

将(26)式代入(27)式得

将(26)、(28)代入(24)得

式(29)就是最优劳动密集度的具体变化规律。下面我们分别考察各个因素对劳动密集度的影响。首先考察人口增长率对劳动密集度的影响。式(29)对n求导并整理得
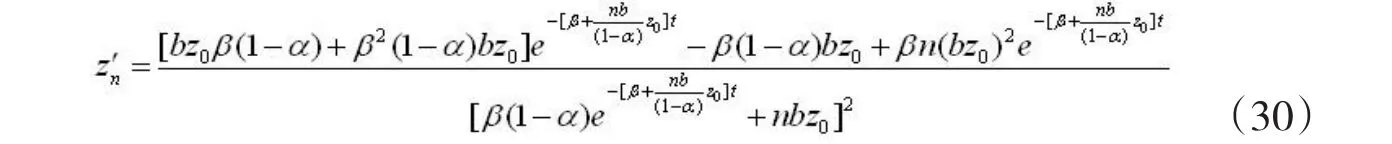
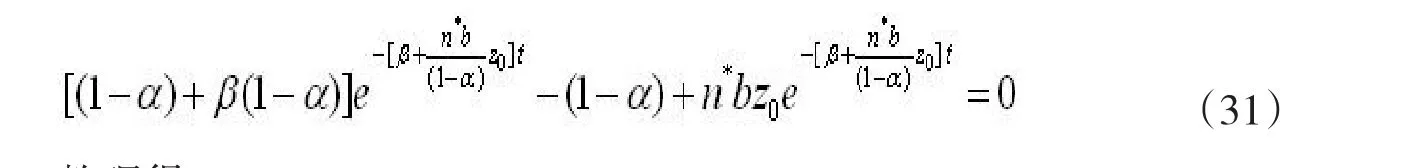
整理得

由(33)式可以得到在t>t*下的n*存在最优值。这意味着,在t>t*情况下,最优劳动密度z与人口增长率n并不总是正相关。在极大值点的左端,最优劳动密度z与人口增长率n是正相关的,在这种情况下人口增长率的提高会导致最优劳动密集度的提高,进而导致经济增长的提高,即“三位一体”:人口增长率提高→劳动密集度提高→经济增长提高。但是在极大值点的右端,最优劳动密度z与人口增长率n是负相关的,这说明如果人口增长率过高会破坏劳动密集度的最优性,进而破坏经济增长的最优性。从劳动密集度对就业的影响而论,在经济增长初期人口增长率的提高与最优劳动密集度的提高同方向,但是达到一定点之后,就业增长率的提高主要不是来自最优劳动密集度的变化,而是来自技术进步引起的分工深化和专业化。
再来考察b对劳动密度z的影响。同样的方法可以算出,劳动密度z相对于b也存在极大值,且二阶导数小于零。这意味着,最初人均物质资本的稀缺会导致最优劳动密集度提高,但是达到一定点之后,人均物质资本的稀缺程度与最优劳动密集度负相关,这说明资源稀缺程度与劳动密集度并非一一对应关系。
最后考察α对劳动密度z的影响,用相同的方法可得,劳动密度z相对于劳动收入比重α也存在极大值,且二阶导数小于零。这意味着,在经济发展初期,收入比例偏重于使用生产资料的劳动,会引起最优劳动密集度的提高,换句话说就是“三位一体”:最优经济增长—高劳动密度—高体力劳动的收入比。但是到了经济发展比较发达阶段,就必须将收入向创造生产资料的脑力劳动方面倾斜,这时的“三位一体”是,最优经济增长—低体力劳动密度—高脑力劳动的收入比。之所以如此是因为,当经济水平达到一定程度后,使用生产资料的劳动变为简单劳动,而制造生产资料的劳动越来越重要。
(二)劳动密集度的最优时间轨迹和最优稳定值
首先考察劳动密集度的最优时间轨迹。对式(24)进行变换得
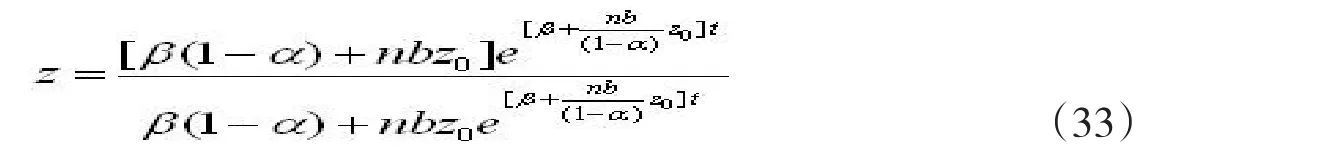
式(33)是人们所熟知的逻辑斯特饱和曲线,因此劳动密集度最优时间轨迹(24)是一条逻辑斯特曲线。这种曲线透露出两个重要信息:一是开始时最优劳动密集度随时间加速递增,二是达到一定点之后减速递增,这一加减速度发生切换的点就是拐点。下面来考察拐点。对(24)求二阶导数得
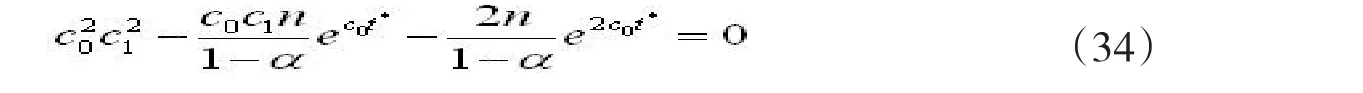
其中t*为拐点时间。将c0、c1代入上式,即可求得拐点时间。在该点的左边,劳动密集度随时间加速递增;在该点的右边,劳动密集度随时间减速递增。
再来考察劳动密集度的最优稳定值。对(24)取极限得

这就是最优稳定值。将代入上式得到稳定的劳动密集度:
(三)稳态下的劳动密度与经济增长
由(29)得

将(29)取极限,并将极限值与(36)式代入(9)得

由(38)式可见,在稳态情况下,经济增长率与劳动密集度呈线性负相关。将稳态的z值代入上式得

式(39)就是稳态情况下经济增长。由该式可见,虽然影响稳定经济增长的因素有许多,但是如果没有科技进步,稳态高速的经济增长是不可持续的。
四、结论
第一,在经济增长率实现最优的情况下,最优劳动密集度是存在的,而且是稳定的,这意味着,在市场经济自动控制下,劳动密集度必然收敛于最优值。因此,劳动密集度不是越高越好,事实上,达到一定点之后再增加劳动密集度则会降低经济增长率。
第二,在经济增长率实现最优的情况下,劳动密集度的时间轨线是一条饱和曲线,最初时最优劳动密集度增长较快,但是达到一定点之后就会大幅度减速。因此,试图采用提高劳动密集度来增加就业之方法并不总是可行的。
第三,提高分工程度是保证高经济增长与高就业同步的根本方法。分工的细化是专业化的结果。专业化并不仅是一个技术问题,从根本上说也是一个观念问题,它深深地根植于一个民族的科学观的土壤之中;科学观作为专业化的基因决定了一个民族对科学和技术的热爱程度和发展方向。中国的落后很大程度上在于观念,我们不是迷恋于科学与技术,而是醉心于政治权力。政治权力只分配财富而不创造财富,只有作为生产力的科学与技术才是创造财富的源泉。
[1]朱殊洋.马克思的生产函数[J].广东行政学院学报,2014,(6).
□责任编辑:周权雄
F016.2
A
1003—8744(2015)05—0100—06
*本文系教育部人文社会科学基金课题(编号:13YJA790129)的阶段成果。
2015—7—31
徐跃华(1964—),女,广州大学马克思主义学院副教授,主要研究方向为经济增长理论;朱殊洋(1959—),中共广州市委党校经济学教研部教授,主要研究方向为政治经济学。

