砂土中带裙板防沉板基础竖向承载力的上限解

刘 润，陈广思

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

随着人类对海洋油气资源的开发由浅海向深海迈进，传统的固定式海洋平台已经不能满足深海油气资源开发的需要，因此应用到深海领域的水下生产系统，逐渐成为深海油气资源开发的主要装备。由于水下生产系统要安装在水下且地质条件复杂的深海海底，地基基础的稳定性是保证整个系统安全运行的前提，防沉板就是一种适用于深海水下生产系统的浅基础。在防沉板的地基稳定性设计中，其竖向承载特性的研究至关重要。目前，国外的防沉板基础设计已经相对成熟，并应用到北海、墨西哥湾、巴西等深海油气田的工程建设中。而我国对防沉板基础的研究尚处于起步阶段，工程设计的主要依据是国外规范［1-2］(如API、DNV)。因此，研究水下生产系统防沉板基础设计计算方法可以为我国东海及南海等深海海域的油气资源开发提供有力的技术支持。

在国内，谭越等［3］以我国南海300 m水深某油田的设计为例，对防沉板的地基承载力与沉降等进行了计算分析，为我国防沉板基础的设计提供一个可参考的实例。在国外，White等［4］针对不同形式的防沉板基础展开了软土地基上的竖向承载力和抗拔力试验研究，得出了防沉板基础竖向承载力和抗拔力与其底部格栅布置形式之间的规律;Tapper等［5］对带裙板的格栅基础进行竖向-水平-弯矩三自由度加载试验，取得了复合加载模式下该种基础的地基破坏包络面及相应的地基破坏模式。虽然以上学者对防沉板基础的研究取得了有益的成果，但是对带裙板防沉板在竖向承载模式及竖向承载力计算方面的专题研究较少。

在岩土工程研究中，通常将较为复杂的基础形式简化为条形基础或方形基础进行研究，以此来简化分析过程［6-9］。从防沉板基础的分类来看，属于浅基础。对于浅基础来说，比较经典的竖向承载力计算公式有Terzaghi公式［6］，Meyerhof公式［7］，Hansen 公式［8］和 Vesic 公式［9］等。与传统浅基础不同的是，防沉板基础的底部四周带有加强承载力的裙板，裙板的存在使防沉板基础的竖向承载力计算有别于传统的浅基础。因此，本文将带裙板防沉板基础简化为带裙板条形基础进行研究，建立了特有的竖向承载模式。通过极限分析上限定理推导了带裙板条形基础的地基承载力。提出了一个能够反映裙板与基础内部土体共同作用的经验参数—土体破坏率(η)。通过与文献中带裙板条形基础的竖向承载力模型试验相对比，确定了土体破坏率的数值，并分析了在不同土体破坏率情况下，地基承载力系数与土体内摩擦角之间的关系。

1 带裙板条形基础承载力的上限解

在极限分析理论中，如果假设破坏模式满足速度边界条件及应变与速度的相容条件，根据外功率等于机构变形所消耗内功率的原则，可以得到作用于机构外部的荷载，该荷载不会小于机构破坏时的真实荷载，因此求出的解即为荷载的上限解。有关上限解的理论已经在文献［10-13］中作了详细论述，这里不再赘述。

1.1 基本假定

由极限分析上限法的原理可知，该方法的求解关键是建立一种满足速度边界条件及应变与速度相容条件的破坏模式。根据已有的研究结果［14-18］可知，带裙板条形基础竖向承载力有如下特点:

1)具有相同高度和宽度条件下，带裙板条形基础比实体条形基础竖向承载力低;

2)基础宽度一定的条件下，带裙板条形基础竖向承载力随着基础高宽比的增加而增大;

3)基础高度一定的条件下，带裙板条形基础竖向承载力随着基础高宽比的增加而减小。

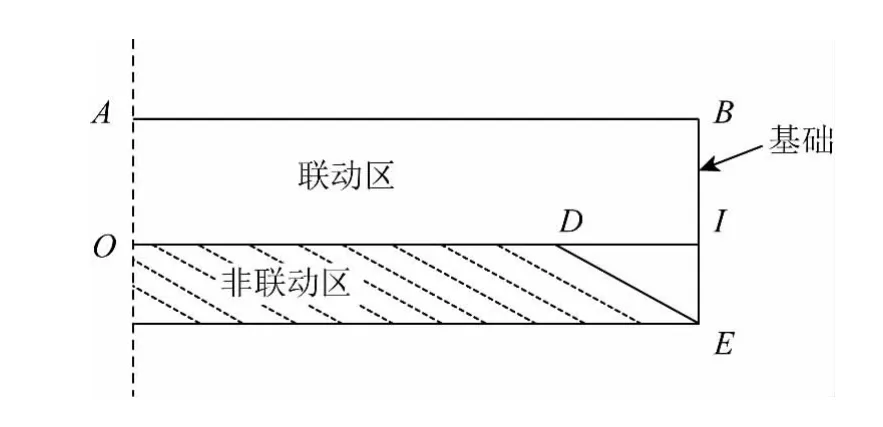
图1 基础内部土体承载模式Fig.1 The bearing mechanism of inner soil of foundation

与此同时，与实体条形基础相比，带裙板条形基础裙板约束范围内为刚度相对较弱的土体，为了反映与实体条形基础的差异，分析中将裙板约束范围内土体划分为联动区与非联动区，联动区在基础底板的约束下与基础一起运动，可以视为基础的一部分，而非联动区土体受到的基础约束力较小，不能视为基础的一部分，由部分的主动区及过渡区组成，如图1所示。

引入土体破坏率这一参数，记为η，来描述基础内部土体非联动区范围的大小。

式中:lIE表示基础内非联动区土体高度，B表示基础宽度。则基础内非联动区高度为ηB/2，联动区土体高度BI为(H-ηB/2)，H表示基础裙板高度。

基于以上的研究结论与假设，参考经典地基承载力计算公式中Terzaghi公式的基本假定，提出了带裙板的条形基础的竖向承载模式，即Terzaghi破坏模式(T模式)。

1.2 Terzaghi假设破坏模式(T模式)

1.2.1 几何尺寸

图2为带裙板条形基础的Terzaghi破坏模式。

由于对称性取基础的一半进行分析，将地基中土体的滑动面分为五个区域，即:联动区OABED;主动区 OCD;过渡区 CDH;被动区 EHF;边载区BEFG。其中联动区OADEB，主动区OCD，过渡区CDH的假设与M模式相同，被动区EHF为一个等腰三角形位于过渡区CDH右侧，且底角α为(π/4-φ/2)。边载区BEFG位于被动区EHF的上方。土体破坏率为η，几何尺寸不同，计算如下:

图2 带裙板条形基础Terzaghi破坏模式Fig.2 Terzaghi mechanism of skirted strip foundation

1.2.2 速度场

如图2所示，根据极限分析上限定理，设基础完全破坏时以速度v0向下运动，则可以推导出速度间断面CD，CH，及HF的速度:

在间断面CD上:

在间断面CH上:

式中:θ为CD与DH之间的夹角。

在间断面HF上:

1.2.3 重力做功

1)联动区OABED部分

联动区OABED重力做功功率为:

式中:SOABED为联动区OABED的面积，即:

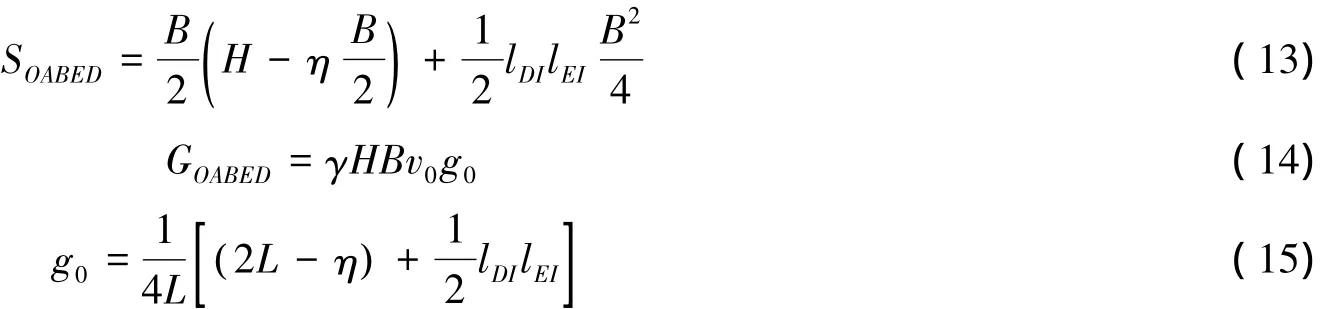
其中，L=H/B为高宽比。

2)主动区OCD部分

主动区OCD重力做功功率为:

式中:SOCD为主动区OCD的面积，则:

3)过渡区CDH部分

如图1所示，过渡区CDH重力做功功率为:

则:

4)被动区EHF部分

被动区EHF重力做功功率为:

式中:

边载区BEFG重力做功功率为:

1.2.4 极限承载力公式

T模式下的极限荷载PT做功为PTv0/2，由上限定理可知，外力总功率等于能量耗散率，则地基承载力上限解为:

1.3 确定土体破坏率

由以上分析可知，确定土体破坏率是计算地基竖向承载力的关键。应用文献［14］中不同高宽比的带裙板条形基竖向力承载试验数据对η进行反算，如果土体破坏率取某一数值时与试验值较吻合，则可确定此时的土体破坏率。该试验用土的参数见表1所示。

表1 文献［14］中试验土体参数Tab.1 Properties of the sand in literature［14］

由试验数据计算的ηT结果见表2所示。

表2 η的计算值Tab.2 The calibration values of η

从表2中可以看出，当基础高宽比小于等于1时，η的反算结果均大于10%;当基础高宽比大于1时，η的反算结果均小于10%。这是由于随着基础高宽比的增加，土体会在基础底部形成土塞，减小了基础内部土体的破坏程度。根据上面的分析，将η与H/B的关系绘制于图3中。

从图3可以看出，在T模式下随着基础高宽比的增加，土体破坏率η在减小，拟合得到η与H/B的关系如下:

图3 T模式下η与H/B关系Fig.3 The relationship between η and H/B in T mechanism

实际工程中防沉板基础高宽通常小于1，由图3可知，此时土体的破坏率大于10%。

2 地基承载力系数的讨论

2.1 承载力系数Nq

在前人的研究中，针对条形基础的竖向承载力系数Nq已经取得了精确的结果:

本文提出的竖向承载力系数考虑了基础内部土体破坏率的影响，以H/B=0.5为例，对比NqT与经典公式中Nq值的差异，结果见图4所示。

从图4可以看出，利用T模式计算的地基承载力系数NqT均小于经典公式中的Nq值，原因在于，联动区的提出使得采用本文提出的公式计算NqT时要考虑来自基础内部土体的作用;土体破坏率的设定使得在基础边载的影响范围小于等宽的条形基础。

2.2 承载力系数Nγ

竖向承载力系数Nγ的研究成果亦较多。其中较为经典的有Meyerhof(1951)公式、Hansen(1970)公式和Vesic(1973)公式:

在砂土中，内摩擦角大于30°，以基础的H/B=0.5为例对比了NγT与经典Nγ值的差异，结果见图5所示。

图4 T模式与经典公式的Nq比较Fig.4 Comparison of Nqwith T mechanism and classical formula

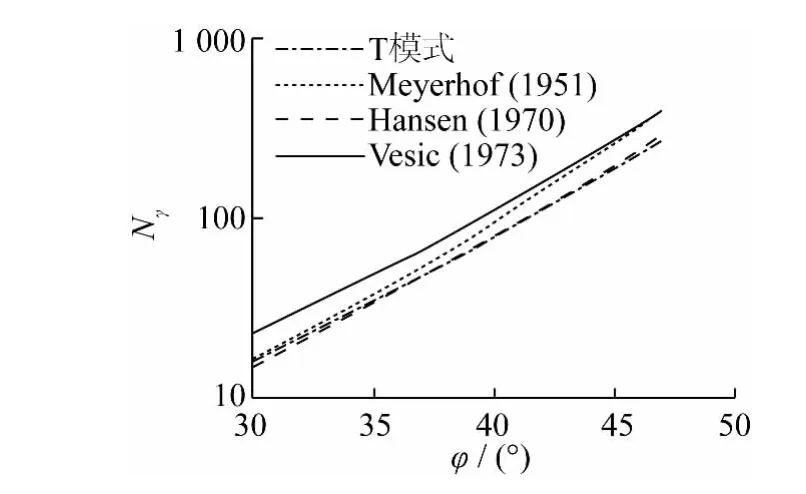
图5 T模式与经典公式的Nγ比较Fig.5 Comparison of Nγwith T mechanism and classical formula

从图 5 可以看出 NγT小于 NγMeyerhof和 NγVesic，与 NγHansen较为接近。

3 土体破坏率对地基承载力系数的影响

由于带裙板条形基础内部土体与传统的实体基础相比刚度存在较大的差异，且基础内部土体的破坏程度与基础的高宽比相关，因此土体破坏率的取值对带裙板条形基础竖向承载力的计算有较为显著的影响。为了揭示土体破坏率对地基承载力系数的影响规律，以下选取高宽比为0.3、0.4、0.5、0.6和0.7的带裙板条形基础进行分析。

由式(33)计算可得高径比为0.3至0.7的带裙板条形基础土体破坏率η分别为13.3%、12.8%、12.3%、11.8%和11.3%。图6和表3给出了η在12.8%到14.8%范围内变化对地基承载力系数NqT的影响。

从图6及表3中可以看出，内摩擦角在30°到47°范围内时，不同η下的NqT都随内摩擦角的增大而增大，但η为12.8%时增幅最快，η为14.8%时增幅最慢。内摩擦角相等时，NqT随着η的增大而减小。

图7及表4给出了η在12.8%到14.8%范围内变化对地基承载力系数NγT的影响。

图6 不同η下的NqT的比较Fig.6 The comparison of NqTwith different η

图7 不同η下的NγT的比较Fig.7 The Comparison of NγTwith different η

表3 不同η下的NqT计算值Tab.3 The value of NqTwith different η

表4 不同η下的NγT计算值Tab.4 The value of NγTwith different η

从图7及表4中可以看出，内摩擦角在30°到47°范围内时，不同η下的NγT都随内摩擦角的增大而增大，但η为12.8%时增幅最快，η为14.8%时增幅最慢。内摩擦角相等时，NγT随着η的增大而减小。以上变化规律与NqT随η变化规律相同，但从NγT数值上分析，NγT对η的敏感性要高于NqT。

4 结语

针对深海水下生产系统的主要基础型式——防沉板，将其简化为带裙板条形基础进行研究，推导得到了竖向承载力的上限解，主要结论如下:

1)为了反映群板约束范围内土体在一定程度上与条形基础共同承担上部荷载的特点，将裙板内土体划分为联动区与非联动区，同时假定了基底以上边载区土体的不同滑动面，提出了T竖向承载模式。

2)运用极限分析上限法，推导了基于T模式的竖向承载力计算公式，引入了土体破坏率(η)参数，反映受到基础底板约束的板内土体范围，建立了T模式下η与基础高宽比的关系。

3)受土体破坏率的影响，高宽比为0.5的带裙板条形基础在T模式下的NqT均小于经典公式中的Nq值，NγT小于 NγMeyerhof和 NγVesic，与 NγHansen较为接近。随之 η 的增大，在内摩擦角不变的情况下，NqT和 NγT降低，且NγT对土体破坏率的敏感性要高于NqT。

［1］ API RP 2A，Recommended practice for planning，designing，and construction fixed offshore platforms［S］.American Petroleum Institute，2000.

［2］ DNV，Classi fi cation notes No.30.4，Foundations［S］.Norway:Det Norske Veritas，1992.

［3］ 谭越，石云，刘明.管道终端及防沉板基础分析［J］.海洋石油，2011，31(3):93-96.(TAN Yue，SHI Yun，LIU Ming.Structure analysis of PLET and mudmat［J］.Offshore Oil，2011，31(3):93-96.(in Chinese))

［4］ WHITE D J，CHEUK C Y，SPRINGMAN S M，et al.An investigation into the vertical bearing capacity of perforated mudmats［C］//Proceedings of the International Symposium on Frontiers in Offshore Geotechnics.2005.

［5］ TAPPER L，BYENE B W，MARTIN C M.Combined load capacity of grillage foundations on loose sand［C］//Proceedings of the 8th International Conference on Physical Modelling in Geotechnics.2014.

［6］ TERZAGHI K.Theoretical soil mechanics［M］.Wiley，New York，1943.

［7］ MEYERHOF G G.The ultimate bearing capacity of foundations［M］.Geotechnique，The Institution of Civil Engineers，London，1951:301-332.

［8］ HANSEN J B.A revised and extended formula for bearing capacity［M］.Danish Geotechnical Institute Bulletin，1970:5-11.

［9］ VESIC A S.Analysis of ultimate loads of shallow foundations［J］.Proc.，ASCE，1973，99(1):45-73.

［10］韩长玉，夏小和，王建华.底面为曲面基础地基极限承载力上限解［J］.岩土工程学报，2012(2):230-236.(HAN Changyu，XIA Xiaohe，WANG Jianhua.Upper bound solutions of ultimate bearing capacity of curved footing［J］.Chinese Journal of Geotechnical Engineering，2012(2):230-236.(in Chinese))

［11］张国祥，付江山.基于极限分析的圆形浅基础地基承载力上限解［J］.岩土力学，2010(12):3849-3854.(ZHANG Guoxiang，FU Jiangshan.Upper bound solution for bearing capacity of circular shallow foundation based on limit analysis［J］.Rock and Soil Mechanics，2010(12):3849-3854.(in Chinese))

［12］ CHEN W F.Limit analysis and soil plasticity［M］.London:Elsevier Scienti fi c Publishing Company，1975:637.

［13］ SOUBRA A H.Upper-bound solutions for bearing capacity of foundation［J］.Journal of Geotechnical and Geoenvironmental Engineering，1999，125(1):59-68.

［14］ EID H T.Bearing capacity and settlement of skirted shallow foundations on sand［J］.International Journal of Geomechanics，2013，13(5):645-652.

［15］ AL-AGHBARI M Y，MOHAMEDZEIN Y E-A.Bearing capacity of strip foundations with structural skirts［J］.Geotechnical and Geological Engineering，2004，22:43-57.

［16］ GOLMOGHANI-EBRAHIMI S，ROWSHANZAMIR M A.Experimental evaluation of bearing capacity of skirted footings［J］.Civil Engineering and Architecture，2013，1(4):103-108.

［17］EID H T，ALANSARI O A，ODEH A A，et al.Comparative study on the behavior of square foundations resting on confined sand［J］.Canadian Geotechnical Journal，2009，46:438-453.

［18］刘润，王磊，丁红岩，等.复合加载模式下不排水饱和软粘土中宽浅式筒型基础地基承载力包络线研究［J］.岩土工程学报，2014，36(1):146-154.(LIU Run，WANG Lei，DING Hongyan，et al.Study on failure envelopes of large diameter shallow buried bucket foundation in undrained saturation soft clay under combined loading conditions［J］.Chinese Journal of Geotechnical Engineering，2014，36(1):146-154.(in Chinese))