冰激直立腿海洋平台疲劳寿命分析

张大勇，刘 笛，许 宁，岳前进，郭龙玮

(1.大连理工大学海洋科学与技术学院，辽宁盘锦 124221;2.大连海洋大学航海与船舶工程学院，辽宁大连 116023;3.国家海洋环境监测中心，辽宁大连 116023)

我国渤海油气资源主要由导管架平台开发。出于经济性考虑，平台通常设计具有足够的刚度抵御波浪荷载。但对于动态冰荷载，往往没有充分考虑，导致平台水平刚度相对冰荷载较低。多年的现场监测发现，导管架平台固有频率与海冰的破碎频率较为接近，在冰振作用下导管架平台属于典型的柔性结构，动力效应显著［1］。强烈的冰激振动不仅会造成作业人员不适、上部设施损坏，还会引起平台管节点疲劳损伤，因此，在抗冰结构设计和安全保障中很有必要开展冰激疲劳寿命分析［2-3］。

柔性直立桩腿抗冰结构是结冰海域一种常见的结构形式。比如导管架海洋石油平台、海上风力发电塔、桥墩、灯塔等。这些结构在冰力作用下能产生较大的变形，在周期性冰力作用下能产生显著的振动问题。美国石油协会的寒区海洋石油平台设计建议标准指出，必要时需对冰荷载引起的疲劳损伤进行评估，但并没有指出需要进行冰激疲劳分析的具体条件与方法，其原因是尚不具备详细疲劳分析的条件，动冰力模型与冰疲劳环境参数的研究尚不成熟［4］。国内学者方华灿等对抗冰平台冰激疲劳分析做了大量的研究工作，包括:低温钢材疲劳性能的研究，冰荷载作用下疲劳等效应力的计算方法，冰激疲劳可靠性研究［5］。为了解决目前国内外规范中缺乏低温冰荷载作用下的疲劳性能问题，方华灿等提出了综合计算等效应力幅的新方法，给出了管节点的疲劳寿命曲线及其计算参数［6］。李刚等提出了相对冰速、冰厚随机冰载的管节点疲劳应力幅近似计算方法和时变疲劳可靠性分析方法［7］。刘健等基于海洋平台自激振动Maattanen模型，计算了实际平台的冰激振动响应和节结疲劳寿命［8］。岳前进等基于现场观测，对渤海抗冰导管架平台冰激疲劳寿命估计的必要性进行分析，明确了锥体平台疲劳冰荷载与冰环境参数的研究方法［9］。但是对于进行具体的冰激直立抗冰平台疲劳寿命分析还需开展进一步工作。

基于多年的现场监测，分析冰与直立结构相互作用过程，并提出冰激直立腿抗冰平台的疲劳寿命分析流程。选取渤海某典型直立腿抗冰平台，利用ANSYS数值模拟，采用安全寿命设计方法，对比了稳态冰力和随机冰力下直立抗冰结构的疲劳损伤，进而计算出冰激疲劳寿命。

1 冰与直立腿抗冰结构的相互作用

冰与直立结构作用时，可能出现劈裂、弯曲、屈曲和挤压等多种破坏形式，其中以挤压破坏为主。随着冰速变化，挤压冰力可以分为三种模式:低冰速时的准静态冰力;中冰速时的稳态冰力;快冰速时随机冰力。其中，稳态冰力对结构影响最大，而快冰速下的随机冰力占据绝大数冰况［3］。

1.1 准静态冰力

在冰速很慢(v＜2 cm/s)且冰面比较平整时，冰会发生准静态(间歇)挤压破碎，结构发生准静态振动。冰力周期远大于结构自振周期，结构准静态振动很少发生，持续时间短，振幅低，因此在冰振疲劳分析中可以忽略不计。

1.2 稳态冰力

当冰与结构作用速度缓慢增加，快于间歇性挤压破碎时冰速(2 cm/s＜v≤4 cm/s)，冰的破碎过程会与结构振动产生耦合，此时发生频率锁定的稳态冰力，结构发生简谐形式的稳态自激振动。现场观测发现，结构自激振动发生时，结构振动频率与荷载频率锁定，结构发生稳态共振，振幅较大，如图1所示，其中锯齿状的时程曲线是挤压交变冰力，光滑曲线是结构的振动位移。自激振动发生需要冰速与结构运动速度处于一种临界状态，通常其发生概率较低。由于自激振动强烈而且稳定，决定了在结构的疲劳失效分析中，需要计算自激振动造成的累积损伤［10］。

图1 稳态振动发生时冰力和结构动位移的同步时程Fig.1 The ice force and vibration displacement during the steady state vibration

Kärnä［11］根据渤海实测的自激振动冰力时程，给出了简化的三角波时域函数，表征产生自激振动的冰力随时间的变化特征，如图2所示。

图2 稳态冰力模型Fig.2 The ice force model of steady state

Fmax是冰力最大值，可保守取为极值静冰力:

其中，β是系数，根据窄体结构静冰力现场和室内研究成果，取0.7;σc是海冰的单轴压缩强度，采用现场试验结果，取为2.0 MPa;h是冰厚，m;D是冰与结构接触宽度，即桩腿直径，m;ΔF=qFmax，q=0.1～0.5;Fmean是冰力平均值，可通过Fmax-ΔF/2计算;T为冰力周期，计算中可近似取为结构固有周期;α是加载阶段系数，通常选取0.6～0.9，文中取0.7。

1.3 随机冰力

当冰速很快时，冰板在桩腿上发生连续不规则的脆性挤压破碎，由于接触面上冰的碎块大小不一，且压力分布不均，由此形成的合力为不规则的随机变化，同时引起结构的随机振动。图3是基于实测的随机挤压冰力和结构振动的时程曲线。由于直立结构在快速冰力的挤压破坏时产生的强迫随机振动占绝大数工况，因此在疲劳分析中应当考虑。

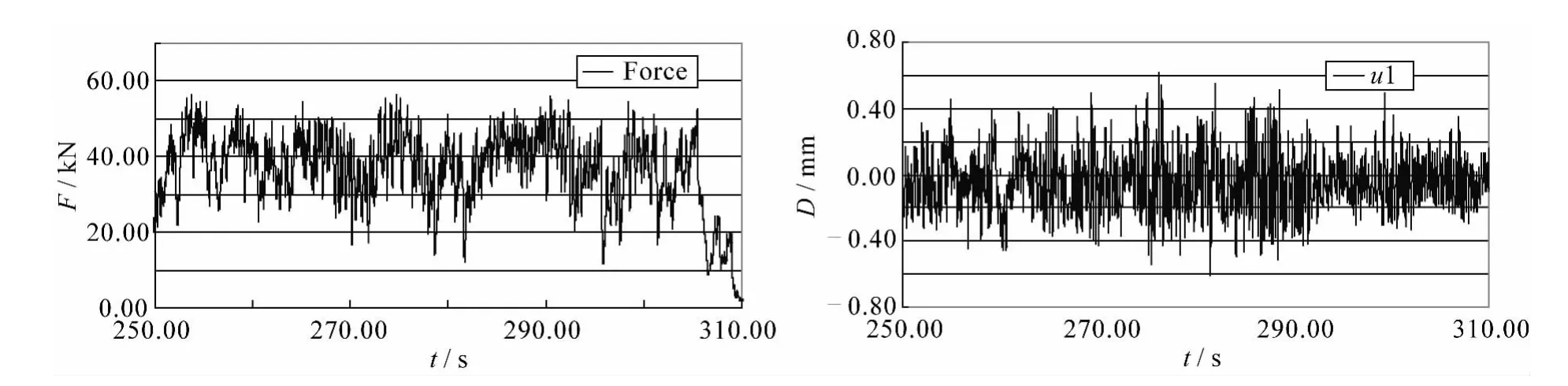
图3 随机动冰力和结构随机振动时程Fig.3 The random ice force and structural vibration

Kärnä等［12］根据渤海和波斯尼亚湾灯塔上测得的大量样本的随机冰荷载数据，经过统计分析建立了随机冰力谱:

以上论述中发现，冰与直立腿抗冰结构相互作用过程中，稳态冰力和随机冰力对导管架管节点疲劳损伤影响较大，需要重点考虑，进而估计平台冰振疲劳寿命。

2 冰激直立结构疲劳寿命分析方法

对于海洋结构来讲，安全寿命设计方法比较成熟，适于冰激结构疲劳寿命估计。目前，各国平台规范普遍推荐安全寿命分析方法作为海洋平台构件疲劳分析与评价的主要手段［13］。因此，本文选取安全寿命设计方法进行冰激疲劳寿命估计。安全寿命分析方法主要是基于Miner线性累积损伤理论和材料的S-N曲线。

2.1 Miner线性累积损伤理论

若构件在某恒幅应力水平S作用下，循环至破坏的寿命为N，则可定义其在经受n次循环时的损伤为:

显然，若n=0，则D=0，构件未受到疲劳损伤;若n=N，则D=1，构件发生疲劳破坏。

构件在应力水平Si作用下，经受ni次循环的损伤为Di=ni/Ni。若在k个应力水平Si作用下，各经受ni次循环，则可定义其总损伤为:

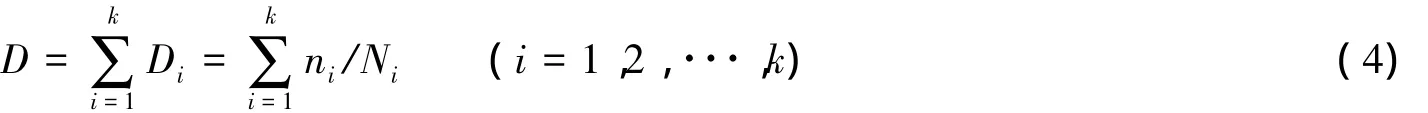
破坏准则为:

其中，ni是在Si作用下的循环次数，由荷载谱给出;Ni是在Si作用下循环到破坏的寿命，由S-N曲线确定。

2.2 S-N曲线

材料的疲劳性能，用应力水平S与破坏时的寿命N之间的关系描述。对于承受环境荷载引起的交变应力的管连接，采用“海上固定平台规划、设计和建造的推荐作法”给出的S-N曲线(X和X'曲线)，用数学式表达如下［14］:

式中:Δσ即应力范围，Δσref及m值如表1。其中，X曲线是适用于相邻母材具有光滑的熔透焊接并进行焊缝外形控制的节点，若剖面控制不当，则推荐使用X'曲线。

表1 S-N曲线参数表Tab.1 Parameters of S-N curve

2.3 疲劳应力分析

疲劳应力分析中，疲劳损伤及寿命计算通常有两种常用的方法:时间域法、谱方法。

时间域法，可以获得各个疲劳工况下各个子工况所对应的管节点热点应力时间历程。由于疲劳寿命分析中需考虑多个疲劳子工况，采取时间域法，计算工作量相当大;此外，时间域分析的前提条件是具有适用性的冰力函数，而目前快冰速下挤压冰力很难用冰力时程函数给以准确描述。谱分析是一种考虑荷载随机特性，并用统计方法描述工况的方法。假定冰力在短时间内是各态历经、窄带平稳的正态过程。根据应力循环是冰力循环转换的观点，假定构件的应力分布为窄带随机正态过程，其峰值为瑞利分布［15］。根据随机振动理论，这一假定具有很高的精度。谱分析方法与时间域分析方法相比，计算效率高，比较适合冰激疲劳寿命估计。

前文指出，冰激直立结构疲劳分析需考虑冰致结构稳态振动和随机振动。对于稳态振动，根据Kärnä［11］给出的简化三角波时域函数，采用时间域法进行分析;对于随机强迫振动，结合Kärnä和Qu［12］建立的随机冰力谱函数，采用谱分析法分析。

冰激平台疲劳寿命估计流程如图4所示，包括稳态振动疲劳寿命计算和随机振动疲劳寿命计算，主要的步骤如下:

1)建立结构力学模型

根据结构的几何性质和物理性质确定结构的振型和频率。几何性质包括结构的总尺度、杆件和节点的数量、杆件的长度及截面积等。物理性质包括结构的刚度、质量及阻尼。

2)建立冰疲劳环境模型

依据海冰作用方向，冰厚和冰速划分冰况，统计每种冰况出现的概率。

3)确定冰荷载模型

稳态冰力模型，参考式(1);冰力谱模型参考式(2)。

4)结构动力分析

稳态振动过程将各工况下的稳态冰力输入到结构有限元模型中，确定应力较大点，并得到热点应力时程，从而估算出应力标准差。

随机振动过程将各工况下疲劳冰荷载谱输入到结构力学模型中，计算其应力方差，按照瑞利分布确定应力历程循环数曲线。应力峰值的概率密度函数可写为:

式中:P(σ)为应力峰值概率密度;σs为应力标准差。

图4 冰激平台疲劳寿命分析流程图Fig.4 Flow chart of fatigue analysis

5)估算每一冰况应力循环数

作用于结构的每一冰况，在结构构件内每年出现的应力循环数表示为:

式中:d为冰期，d;PLcj为j工况冰情出现概率;f为结构的自振频率，Hz。

6)疲劳寿命估算

利用Miner理论估算危险节点的疲劳损伤，即

由于短时间内冰速、冰厚不变，可以假定管节点应力各态历经，服从正态分布。统计各个工况下管节点应力的标准差，并应用基于高斯分布和Miner线性累积损伤定律的三区间法［9］。根据高斯分布，在±1σ、±2σ、±3σ应力区间内发生的时间分别为68.3%、27.1%、4.33%。对于大于3σ的应力仅仅发生在0.27%的时间内，假定其不造成任何损伤。在进行疲劳计算时，将应力处理成上述3个水平，则第j个冰况下结构的疲劳损伤计算公式可写为:

式中:n1σ，n2σ，n3σ分别为 1σ、2σ、3σ 的实际循环次数;N1σ，N2σ，N3σ分别是根据疲劳曲线查得的 1σ、2σ、3σ 对应的允许循环次数。

这样，结构的疲劳寿命为:

3 实例分析

以JZ20-2SW导管架平台为例，该平台是四桩腿直立结构，上层甲板质量400 t，下层甲板质量900 t。利用ANSYS软件建立有限元模型，上部模块用质量单元mass21模拟;导管架用实际尺寸由管单元pipe16模拟;工字梁用梁单元beam189模拟;入土的部分桩用管单元pipe16模拟，桩-土的相互作用由等效桩模拟(泥面以下6倍桩径)，阻尼比为0.025。建立的有限元模型如图5，利用模态分析，计算结构的频率如表2所示，基频为1.554 Hz，平台实测为1.4 Hz，说明计算模型保证了原结构动力特性的真实性。

表2 平台固有频率Tab.2 The natural frequency of platform

3.1 疲劳工况

图5 平台的有限元模型Fig.5 The finite element model of platform

影响冰力大小的主要因素有冰厚、冰速和冰破碎强度，而冰破碎强度在相同的海域变化不大，因此，这里只选择冰速和冰厚来确定疲劳冰况。最大冰厚取实测最大值30 cm，最大冰速取100 cm/s。冰速的划分以10 cm/s为单位长度，将冰速0～100 cm/s划分为11种工况(0～10 cm/s考虑为2～4 cm/s和4～10 cm/s两种冰况，前者为稳态振动发生的冰况，后者为随机振动冰况)。将冰厚以6 cm为基本单位划分5种工况，一共有55种疲劳冰况。根据渤海海冰疲劳环境模型研究的成果，取两个冰作用方向，分别为45°和225°(以正北向为基准，顺时针为正)［16］。对于该平台，由于结构近似对称，并且在两个主要来冰方向基本是在同一直线上，即最大节点应力出现的位置几乎相同，因此为了简化计算，只考虑一个冰方向。

对于每一种冰况，假定冰速和冰厚的分布是相互独立的随机过程，因此各种冰况下的概率就是冰厚和冰速的联合分布概率，即冰厚和冰速分布概率的乘积。

表3 疲劳冰况出现的概率P(h，v)Tab.3 The probability distribution of the ice conditions

JZ20-2海域的冰期相对有长有短，根据有效冰日的概率分布来计算平均有效冰期，基于多年实测计算出渤海辽东湾有效冰期为42天。

3.2 热点应力计算

结合式(1)和(2)，可以确定出每种冰况下对应的冰力模型，其中各冰况下稳态冰力幅值如表4所示，典型冰况下随机冰力谱如图6所示。输入到平台结构有限元模型中，得到管节点热点处(如图7所示)应力幅值或标准差(单位MPa)。此时，还应根据热点处构件连接形式及尺寸，按照“海上钢结构疲劳强度分析的推荐作法”［17］计算应力集中系数(SCF=8.79)，从而得到管节点真实的应力幅值(稳态振动情况，如表5所示)或应力标准差(随机振动情况，如表6所示)。

表4 各冰况下稳态冰力幅值Tab.4 Steady state ice load amplitude under different ice conditions

图6 直立结构随机冰力谱形式Fig.6 Ice force PSD of vertical structure

图7 管节点热点位置Fig.7 The position of hot spot stress

表5 稳态振动下热点应力幅值Tab.5 The stress amplitude of hot spot induced by steady vibrations (MPa)

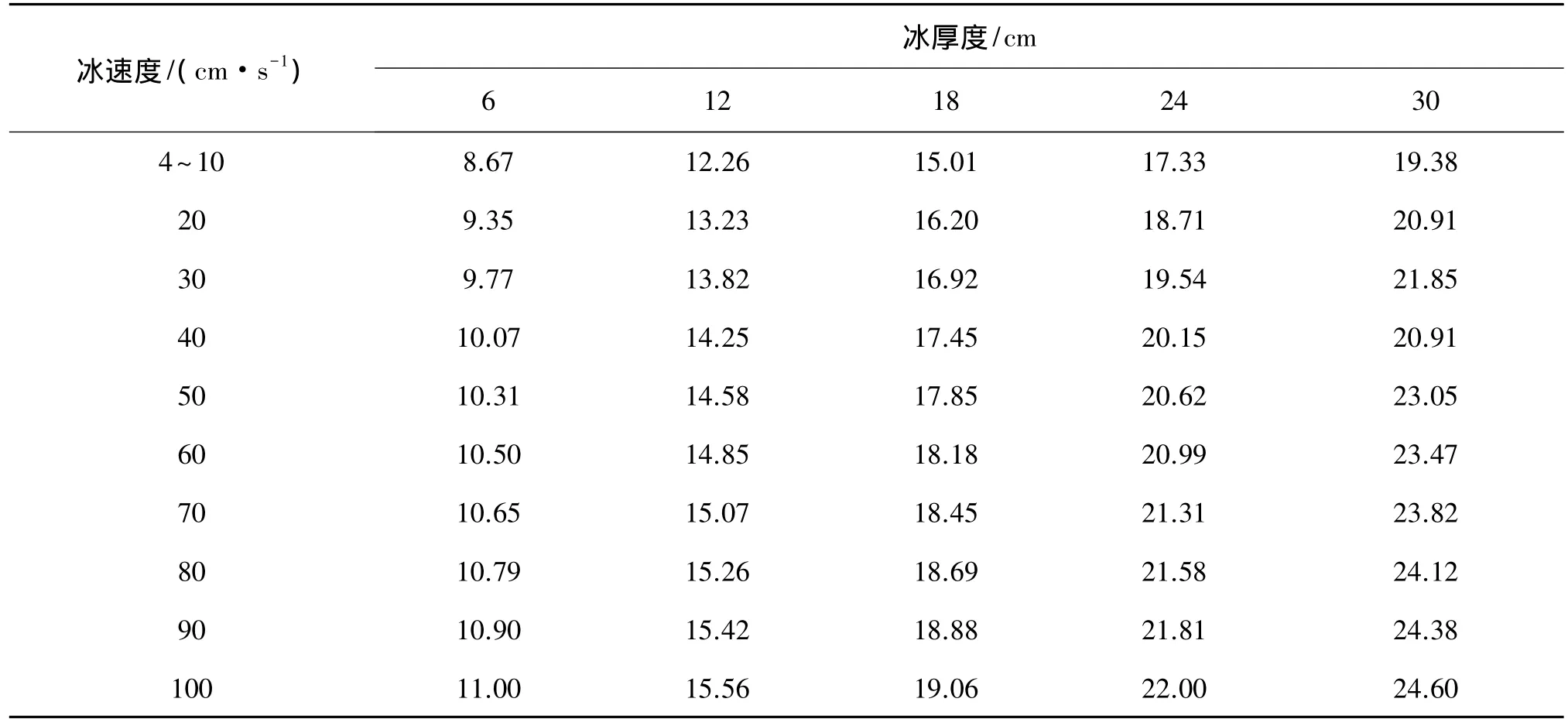
表6 随机振动下热点应力标准差Tab.6 The stress amplitude of hot spot induced by steady vibrations (MPa)

表7 稳态振动时管节点热点疲劳损伤Tab.7 Fatigue damage of hot spot under steady-state vibration (a-1)

表8 随机振动时管节点热点疲劳损伤Tab.8 Fatigue damage of hot spot under random vibration (a-1)

3.3 管节点疲劳损伤及寿命计算

表7、8分别为稳态振动和随机振动冰况下结构的疲劳损伤。分析发现，冰致结构稳态振动可以激起平台较大的热点应力，但稳态冰况出现的概率远远低于随机振动冰况;冰致结构稳态振动引起结构管节点疲劳损伤为2.22E-03 a-1;而随机振动引起的疲劳损伤为6.33E-03 a-1。稳态振动下管节点疲劳应力幅值较大，但稳态冰况出现的概率较低，冰致平台稳态振动的疲劳损伤占总损伤的26%。可见，随机振动是冰激直立腿抗冰结构的疲劳失效的主要因素，而稳态振动在疲劳寿命评估中是不容忽视的。

以上分析可得，该导管架平台在各冰况下的总损伤为8.55E-03 a-1，平台的冰振疲劳寿命约为117 a。对于海洋工程结构，设计疲劳寿命至少为使用寿命的2倍［14］，对于平台主体结构的疲劳分析，文中选取安全系数为5，则该平台冰振疲劳寿命为23 a。

4 结语

基于渤海辽东湾抗冰导管架平台多年的现场监测，明确冰与直立结构相互作用过程，提出一套冰激直立腿抗冰平台的疲劳寿命计算流程。选取渤海某典型直立腿石油平台，利用ANSYS有限元软件，采用安全寿命设计方法，进行了冰振疲劳寿命分析。对比了稳态冰力和随机冰力下直立抗冰结构的疲劳损伤，发现稳态振动可以激起管节点较大的疲劳应力幅值;而随机振动冰况远多于稳态冰况，随机振动引起的疲劳损伤较大。进而计算出冰激直立腿海洋平台的疲劳寿命。本研究对寒区窄体直立腿抗冰结构的设计和安全保障方面具有一定的理论指导意义。

［1］ 张大勇，岳前进，车啸飞，等.抗冰导管架平台动力特性分析［J］.海洋工程，2010，28(1):18-24.(ZHANG Dayong，YUE Qianjin，CHE Xiaofei，et al.Dynamic characteristics analysis of ice-resistant jacket platforms in Bohai Sea［J］.The Ocean Engineering，2010，28(1):18-24.(in Chinese))

［2］ 岳前进，张大勇，刘圆，等.渤海抗冰导管架平台失效模式分析［J］.海洋工程，2008，26(1):18-23.(YUE Qianjin，ZHANG Dayong，LIU Yuan，et al.Failure modes analysis of ice-resistant compliant structures based on monitoring oil platforms in Bohai Gulf［J］.The Ocean Engineering，2008，26(1):18-23.(in Chinese))

［3］ ZHANG D Y，YUE Q J.Major challenges of offshore platforms design for shallow water oil and gas field in moderate ice conditions［J］.Ocean Engineering，2011，38(11):1220-1224.

［4］ 刘圆.抗冰海洋平台动力分析与结构选型研究［D］.大连:大连理工大学，2006.(LIU Yuan.Research on dynamic analysis and structural lectotype of ice-resistant offshore platforms［D］.Dalian:Dalian University of Technology，2006.(in Chinese))

［5］ 方华灿，陈国明.冰区海上结构物的可靠性分析［M］.北京:石油工业出版社，2000.(FANG Huacan，CHEN guoming.Ice reliability analysis of offshore structures［M］.Beijing:Petroleum Industry Press，2000.(in Chinese))

［6］ 方华灿，许发彦，陈国明.冰区海上平台管节点疲劳寿命计算的新方法［J］.中国海洋平台，1997，12(6):259-263.(FANG Huacan，XU Fayan，CHEN Guoming.New method for fatigue-life calculation of ice offshore pipe node［J］.China Offshore Platform，1997，12(6):259-263.(in Chinese))

［7］ LI Gang，ZHANG Dayong，YUE Qianjin.Life-cycle cost-effective optimum design of offshore platforms considering environmental stressors in ice zone［J］.Journal of Offshore Mechanics and Arctic Engineering，2009，131:031501-031509.

［8］ 刘健，陈国明.基于Maattanen模型的冰激疲劳寿命分析［J］.石油大学学报:自然科学版，2004，28(4):89-94.(LIU Jian，CHEN Guoming.Ice-induced fatigue analysis of offshore structures based on Maattanen model［J］.Journal of the University of Petroleum，2004，28(4):89-94.(in Chinese))

［9］ 岳前进，刘圆，屈衍，等.抗冰平台的冰振疲劳分析［J］.工程力学，2007，24(6):159-164.(YUE Qianjin，LIU Yuan，QU Yan，et al.Fatigue-life analysis of ice-resistant platforms［J］.Engineering Mechanics，2007，24(6):159-164.(in Chinese))

［10］岳前进，郭峰玮.冰致自激振动测量与机理解释［J］.大连理工大学学报，2007，47(1):1-5.(YUE Qianjin，GUO Fengwei.Measurement and explanation for its mechanism of ice-induced self-excited vibration［J］.Journal of Dalian University of Technology，2007，47(1):1-5.(in Chinese))

［11］ KäRNä T，IZUMIYAMA K，YUE Qianjin，et al.An upper bound model for self-excited vibrations［C］//Proceedings of 19th International Conference on Port and Ocean Engineering under Arctic Conditions(POAC).2007:177-189.

［12］ KäRNä T，QU Y，KUHNLEIN W.A new spectral method for modeling dynamic ice actions［C］//Proceedings of the 23rd International Conferences on Offshore Mechanics and Arctic Engineering.ASEM，2004:8-16.

［13］张淑茳，史冬岩.海洋工程结构的疲劳与断裂［M］.哈尔滨:哈尔滨工程大学出版社，2005.(ZHANG Shujiang，SHI Dongyan.Fatigue and fracture of ocean engineering structure［M］.Harbin:Harbin Engineering University Press，2005.(in Chinese))

［14］中华人民共和国石油天然气行业标准.海上固定平台规划、设计和建造的推荐作法—荷载抗力系数设计法［S］.北京:石油工业出版社，2003.(Oil and Gas Industry Standard of the People's Republic of China.Recommended practice for planning designing and constructing fixed offshore platform-Load and resistance factor design［S］.Beijing:Petroleum Industry Press，2003.(in Chinese))

［15］姜萌.近海工程结构物—导管架平台［M］.大连:大连理工大学出版社，2009.(JIANG Meng.Offshore engineering structure-jacket platform［M］.Dalian:Dalian University of Technology Press，2009.(in Chinese))

［16］季顺迎，岳前进，毕祥军.辽东湾JZ20-2海域海冰参数的概率分布［J］.海洋工程，2002，20(3):39-43.(JI Shunying，YUE Qianjin，BI Xiangjun.Probability distribution of sea ice fatigue parameters in JZ20-2 sea area of the Liaodong Bay［J］.The Ocean Engineering，2002，20(3):39-43.(Chinese))

［17］中国海洋石油总公司.海上钢结构疲劳强度分析的推荐作法［S］.北京:石油工业出版社，2003.(China National Offshore Oil Corporation.Fatigue strength analysis of offshore steel structure［S］.Beijing:Petroleum Industry Press，2003.(in Chinese))