一种铰接摆式波浪能转换装置结构性能分析及优化

邱守强，苏 成，王冬姣，叶家玮，梁富琳

(1.华南理工大学土木与交通学院，广东广州 510640;2.上海交通大学海洋工程国家重点实验室，上海200240)

能源是人类赖以生存的物质基础，传统的能源供应已不能满足日益增长的人口和生产需要，环境和价格压力迫使人们寻找新的能源供应。海洋中蕴含着丰富和巨大的能量，波浪能就是其中之一。从波浪中提取能量的方式有很多，摆板式波能转换装置则是利用摆板在波浪激励力作用下的动力响应来驱动动力机械进行能量转换和传递。摆板对波浪能量的吸收与其摆幅大小和动力加速度有关，因此对这种能量转换系统进行动力分析及优化控制具有一定的意义。

目前对摆式波浪能转换装置的利用方式主要有两种:一种称为重力摆，即转轴位于摆板的上部，重力作为回复力;另一种称为浮力摆，转轴位于摆板的底端，浮力是回复力。对这两种类型装置的研究有很多，其中对于重力摆的研究以日本学者Watabe最早和最多［1］。Gunawaradane等对Watabe的摆式模型进行了改进研究［2］，表明这种形式的波浪能转换装置具有较好的波能转换效率。浮力摆类型具有和重力摆相似的波浪激励力响应和做功原理，近年来逐渐成为国内外研究的热点，很多新的概念和方法相继出现。如国内赵海涛等人对矩形底铰摆式波浪能转换装置的研究，提出了“摆板密度”的概念［3］;Renzi等提出了对摆板装置特有的“line-absorber theory”等［4-8］。国内早期竺翔明等［9］和左其华［10］曾以线性分析方法对海底铰接柱进行理论分析和模型计算，其中，前者开展了摆板一个自由度的水动力特征、结构振幅及水动力系数的研究，后者进行了二维自由度的分析。冯铁城对漂浮浮筒的波浪力组成进行了计算，对摆式波能转换装置的水动力分析有一定的借鉴作用［11］。李继刚等从做功和阻尼两个方面对摆式波浪能转换装置进行了吸能机制分析［12］。国外在这方面的研究相对成熟，除上述 Renzi等人外，还有 Folley 等［13-14］，Whittaker 等［15］，Henry［16］，Flocarda等［17］对底部铰接摆式波浪能转换装置进行了研究。但上述研究运动方程中均没有计及黏性阻尼的因素影响。少数文献如Oded等则考虑了非线性因素的作用［18］。值得注意的是，国外在进行理论、实验以及数值研究的同时，还进行了实海况试验。如英国的Oyster装置，芬兰的Waveroller装置等［19-20］。

同时，学者对波能转换装置进行优化控制的研究给与了很多的关注。Falnes和Budal于1978年提出了闩控制的概念［21］;Naiko和Nakamura进行了非规则波况下前馈控制的研究［22］;Hoskin等应用Pontryagin原理进行了优化控制［23-24］;Korde对多自由度的波能装置进行了控制分析［25］;Falnes于2002年对实海况条件进行了主动控制的研究等［26］。但是优化控制在随机波浪中的研究和实海况中的应用依然是很困难的问题。

基于上述研究，对一种海底铰接摆式波能转换装置在规则波作用下的动力响应进行了分析，并对一实验室物理模型进行了算例分析。首先对摆式波浪能转换装置进行了模型建立和理论分析，进行了装置压载水以及外加负载阻尼控制的研究，得出了压载和负载阻尼控制对摆式波浪能转换装置波能转换功率核转换效率的影响和区别。

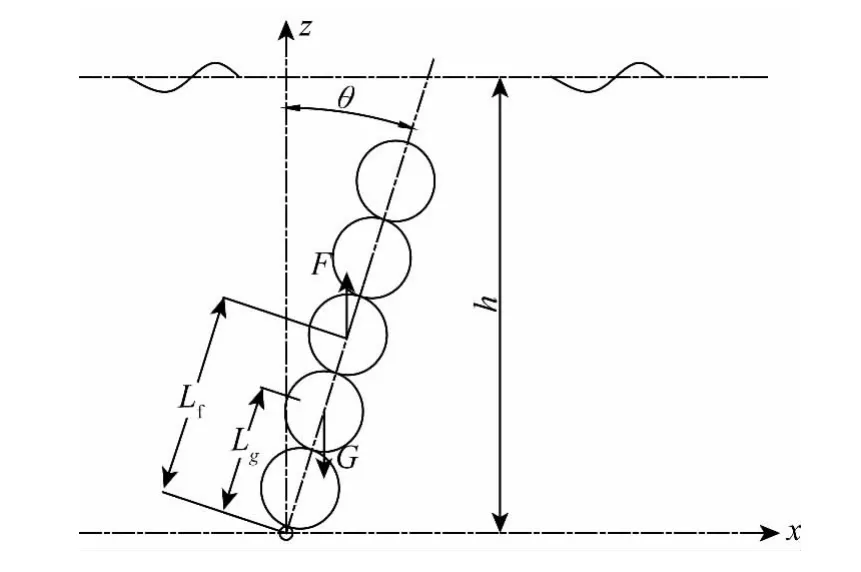
图1 装置物理模型Fig.1 Physical model sketch

1 物理模型

1.1 动力方程的建立

装置模型如图1所示，摆板模型由5个相同直径的轻质玻璃钢空心圆筒组成，底端铰接于一固定转轴，摆板可以绕转轴在垂直于波的传播方向前后摆动。模型原点位于摆板底端转轴(y轴)中心。模型基本参数:R为圆筒半径，G为重力，F为浮力，Lf为浮心高度，Lg为重心高度，h为水深，θ为摆角位移，B为模型宽。定义Tp为模型固有周期，ωp为系统固有频率。模型参数如表1所示。

表1 模型参数Tab.1 Parameters of the model

摆板视为刚体，以线性波及小摆角理论为基础。假设波浪激励力为正弦信号，摆板的运动方程:

式中:I为摆板相对底端转轴的转动惯量;ΔI为摆板运动引起的相对转轴的附加转动惯量;θ(t)为摆板相对其静止平衡位置的摆角位移;cv为摆板在波浪中运动引起的黏性阻尼系数;cr为摆板在波浪中运动引起的辐射阻尼系数;cp为用于吸收波浪能的外加负载阻尼系数;K为系统回复力矩系数;M为波浪激励力矩幅值;ω为波浪激励力角频率大小。

式(1)的解为

其中，θ0为摆角幅值，φ为摆板摇幅响应相对激励力的相位差。摆角幅值和装置的固有频率分别可以为

设定θst=M/K为摆板在静力矩M作用下的摆角大小。由式(3)得，

运动方程式(1)中黏性阻尼系数cv的确定参考船舶横摇运动［27］，将船舶在固有频率下的非线性横摇黏性阻尼系数估算公式线性化，加以修改并推广应用于包含固有频率在内的所有频率的情况，将摆式波浪能转换装置的黏性阻尼系数表示为

式中:κ取0.5。

1.2 计算结果

为了测量模型的自振周期，在实验水槽中进行了模型的衰减实验。在静止的水槽中，将模型倾斜一定角度后放开，然后让其自由衰减，记录摆板倾角位移如图2所示，可知模型的自振周期在5.5 s附近。基于二维势流理论对模型计算的波浪激励力矩M，附加转动惯量ΔI以及辐射阻尼系数cr分别如图3～图5所示，其中入射波高H=15 cm。

图2 衰减实验Fig.2 Decay test

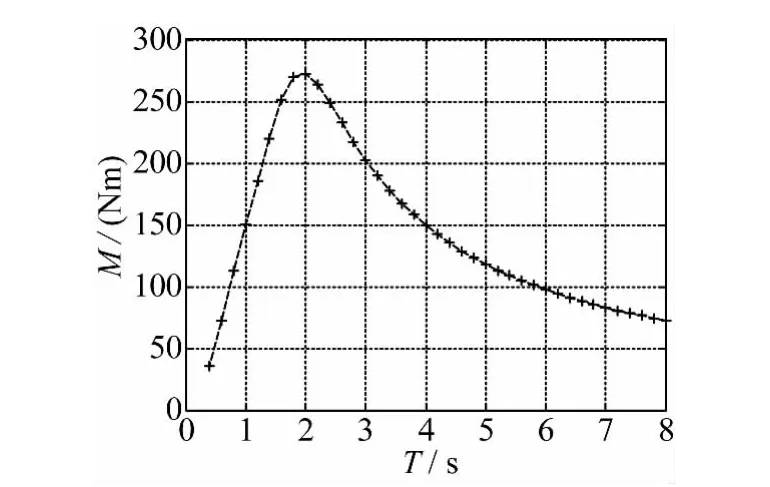
图3 波浪激励力矩Fig.3 Moment induced by waves

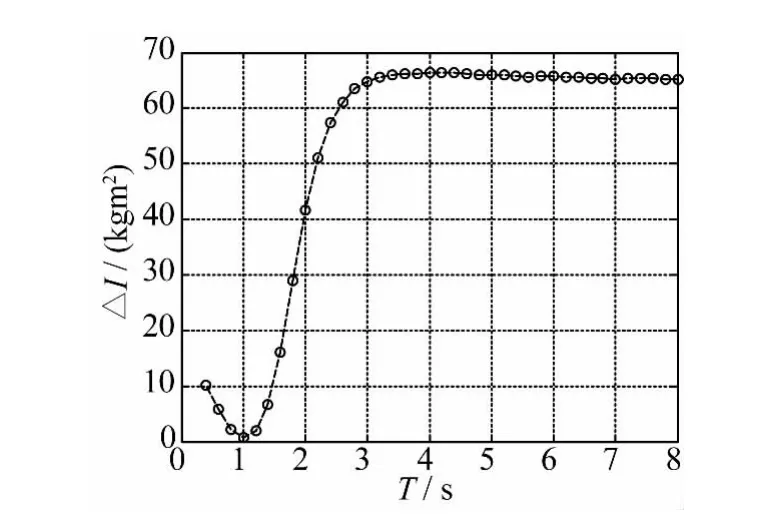
图4 附加转动惯量Fig.4 Added moment of inertia

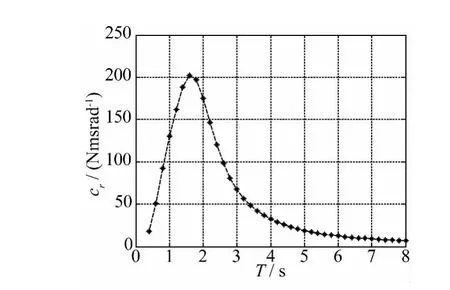
图5 辐射阻尼系数Fig.5 Radiation damping coefficient

由图3可见，波浪激励力矩随着波浪周期的变大先是迅速增大，在2 s附近达到最大值，然后逐渐变小。辐射阻尼系数也有相似的规律(图5)，但是峰值周期在1.5 s左右。附加转动惯量则表现不同，短周期时相对较小，1 s附近较小，然后迅速增加，3 s后接近平稳，同时表明摆板的附加转动惯量在一些周期时要比其自身的转动惯量大的多，因此其固有周期比较大(图2)。图6为模型在不同负载阻尼时摆板动力响应。图示表明，低周期时摆板角度响应相对较小，随着周期的增加逐渐变大，6 s附近具有较大值，然后又变小。阻尼越小，摆板响应越大。图6同时表明摆板的最大响应并不是十分接近模型的固有周期，说明共振周期附近黏性阻尼对模型动力响应具有一定的影响。图7为计及黏性阻尼系数和不计及黏性阻尼系数的摆板运动响应(RAO=2θ0/H)的比较分析，由于实验条件所限，实验波浪周期有限。可见文中所采用的计及黏性阻尼的结果和实验吻合较好。

图6 摆板响应Fig.6 Response of the model

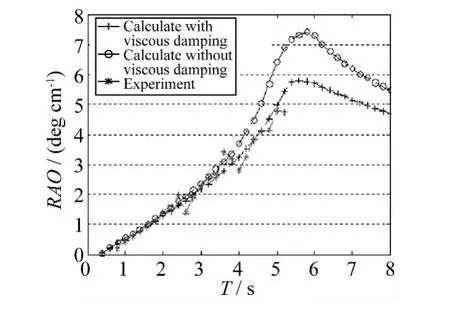
图7 摆板运动响应Fig.7 Response of the model

2 优化控制

规则波中，在负载阻尼系数为cp的波况下，波能转换装置的平均波浪能转换功率［28］:

将摆角位移式(3)代入式(7)得:

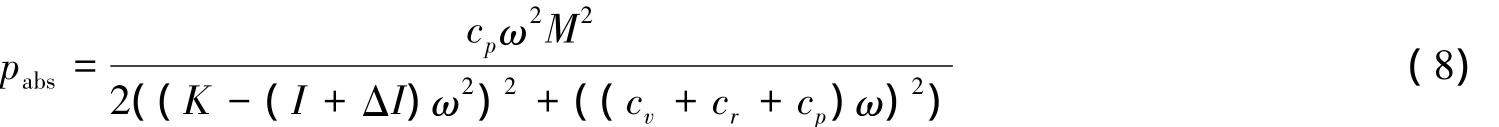
下面将分别对式(8)中的摆板装置回复力矩系数K和用于吸收波浪能的负载阻尼系数cp进行优化，以提高波浪能吸收。其中，回复力矩系数K的优化是对装置进行不同压载水加载的实验;负载阻尼系数cp的优化控制则是多组负载阻尼系数的寻优。

2.1 压载控制

对摆板模型底部4个圆筒分别进行压载水实验，使其转动惯量和回复力矩系数发生变化，研究摆板的质量分布变化对装置波能转换功率和转换效率的影响。不同圆筒的压载状况如表2所示。

表2 不同压载工况Tab.2 Ballast configurations of the model

表2表明，对该种波能转换装置，压载水的变化使其重心重新分布而带来转动惯量和回复力矩的变化，具体表现为装置转动惯量变大，回复力矩变小。但是由图4可知，在大于3 s后的周期时摆板模型的自身转动惯量比附加转动惯量小的多。因此相对其他因素，附加转动惯量对摆板自振频率的影响占据主导因素。

选取负载阻尼cp=100 Nmsrad-1对上述压载工况进行装置波能转换功率和转换效率的分析分别如图8和图9所示。其中，对于波高H、周期T的规则波作用下转换装置宽度范围内的入射波功率Pin可表示为

其中，ρ为水密度，g为重力加速度。

图8 压载控制对波能转换功率的影响Fig.8 Ballast effects on the power absorption

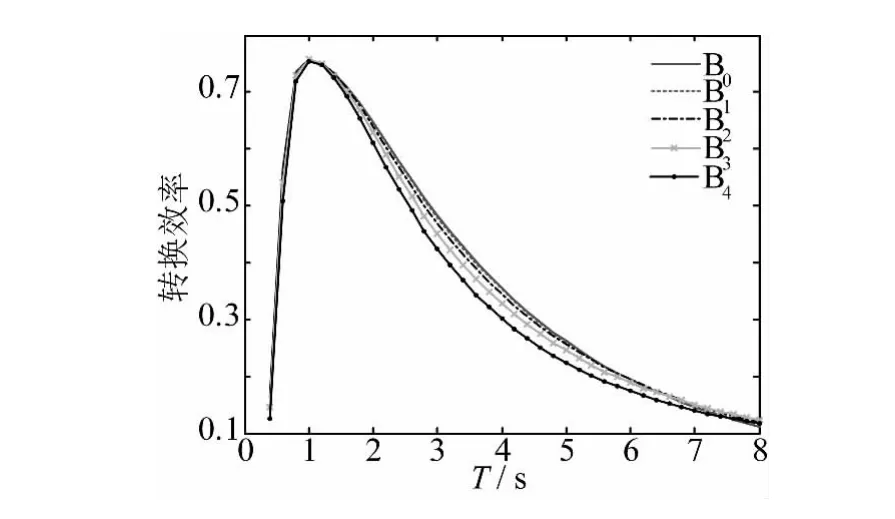
图9 压载控制对波能转换效率的影响Fig.9 Ballast effects on the conversion efficiency

图8和图9表明对该种装置，高频时由于惯性因素占据主导位置，2 s之前各压载工况没有较大区别，2～7 s时回复力矩较大的工况具有相对较好的波能转换功率和效率，7 s之后的表现则刚好相反。总之，对该模型压载的变化对波能转换功率和效率的影响较小。因此，对该种摆式波能转换装置，要使其自振周期与入射波周期保持一致，对于入射波周期大于装置固有周期的波况，可以通过上述的加载压载水进行调解控制，但是对于入射波周期小于装置固有周期的波况，上述方式则不能实现。但是对于重力摆的类型则可以采用上述往圆筒内加载压载水的方式使其固有周期往短周期波方向移动。这里提出解决的方法是可以在装置摆轴的上下位置分别设置若干圆筒来调节压载水，使其可以适应低入射波周期的波况

2.2 负载控制

选取B0的压载工况，研究负载阻尼的变化对装置波能转换功率和效率的影响，结果分别如图10和图11所示。比较图8和图9可知，相对于压载控制，负载阻尼的主动控制表现出较明显的效果。不同负载阻尼对装置波能转换功率和效率的影响不仅在表现在峰值上，而且还在周期轴上表现出差别。图10所示，波能转换功率峰值随负载阻尼的增加而增加，且功率曲线的峰值向短周期方向移动。但是在入射波周期大于5.0 s以后，对于负载阻尼大于60 Nmsrad-1时，较大负载阻尼对应的波能转换功率较小。这与文献［28］具有相似的结论。

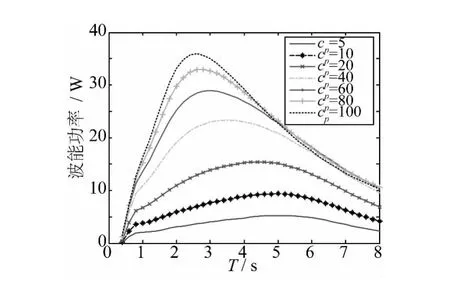
图10 负载阻尼对波能转换功率的影响Fig.10 Applied damping effects on the power absorption

图11 负载阻尼对波能转换效率的影响Fig.11 Applied damping effects on the conversion efficiency

上述研究结果表明，摆式波能转换装置的吸收功率和转换效率对负载阻尼的变化比较敏感。因此，相对于压载控制的方法，该方法的优化控制具有较好的可操作性与现实意义。

同时，研究表明在外加负载阻尼系数cp满足下列条件时具有最佳的波能转换功率和效率［3］，定义cpo为最优负载阻尼系数。

参照式(6)所定义的黏性阻尼系数，对于文中研究的摆式波能转换装置而言，在工况B0时的最优负载阻尼和黏性阻尼系数的曲线如图12所示。

工况B0条件下，选取负载阻尼cp=100 Nmsrad-1作为定常阻尼系数，比较最优负载阻尼系数和定常阻尼系数的波能转换效率如图13所示。

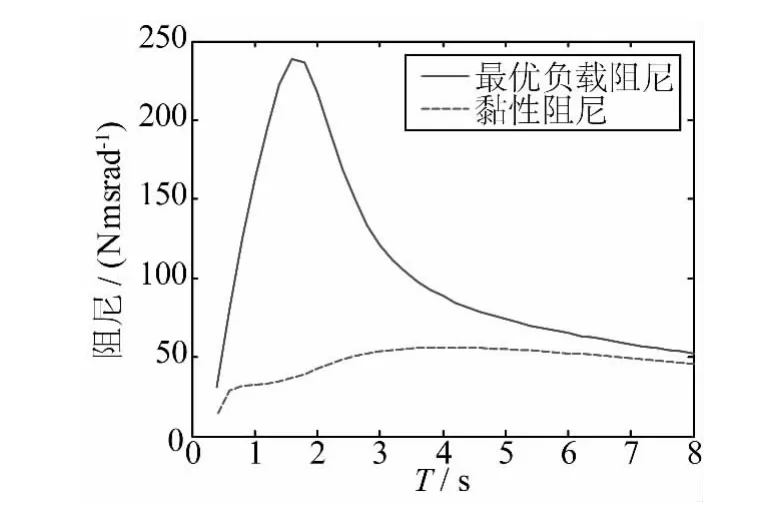
图12 最优负载阻尼和黏性阻尼Fig.12 Optimal damping and viscous damping

图13 最优负载阻尼、定常负载阻尼波能转换效率Fig.13 Conversion efficiency comparison for optimal and constant damping

3 结语

依据线性势流理论对底铰摆式波能转换装置进行了研究，考虑黏性阻尼系数，分析了压载及负载阻尼的优化控制对摆式波能转换装置波能转换功率和效率的影响，得出一些有意义的结论:

1)模型的辐射阻尼和波浪激励力矩随周期的变化相似，在2 s附近具有最大值。附加转动惯量短周期时数值较小，3 s之后变得平稳。

2)摆式波能转换装置的附加转动惯量在一些周期比其自身的转动惯量大得多，因此该种装置的自振周期相对较大。对于底部铰接的浮力摆装置而言，压载水的优化控制对装置波能转换功率和效率的影响效果有限。

3)负载控制表现出比压载控制较好的效果，且负载控制的可靠性和可操作性均较强，更容易实现工程化。工程实际可以采用最优负载阻尼的主动控制进行优化。

［1］ WATABE T，YOKOUCHI H，GUNAWARDANE，et al.Preliminary study on wave energy utilization in Sri Lanka［C］//Proceedings of the Eleventh International Offshore and Polar Engineering Conference.Stavanger:［s.n.］，2001:17-22.

［2］ Gunawaradane.Model study on pendulor type wave energy device to utilize ocean wave energy in Sri Lanka［C］//International Conference on Sustainable Built Environment.2010:297-303.

［3］ ZHAO Haitao，SUN Zhilin，HAO Chunling，et al.Numerical modeling on hydrodynamic performance of a bottom-hinged flap wave energy converter［J］.China Ocean Eng.，2013，27(1):73-86.

［4］ RENZI E，DOHERTY K，HENRY A，et al.How does oyster work?The simple interpretation of oyster mathematics［J］.European Journal of Mechanics B/Fluids，2014，47:124-131.

［5］ RENZI E，DIAS F.Hydrodynamics of the oscillating wave surge converter in the open ocean［J］.European Journal of Mechanics B/Fluids，2013，41:1-10.

［6］ RENZI E，DIAS F.Resonant.Behaviour of an oscillating wave energy converter in a channel［J］.Journal of Fluid Mechanics，2012，701:482-510.

［7］ RENZI E，DIAS F.Relations for a periodic array of oscillating wave energy converters［J］.Applied Ocean Research，2013，39:31-39.

［8］ RENZI E，ABDOLALI B，BELLOTTI G，et al.Wave-power absorption from a finite array of oscillating wave surge converters［J］.Renewable Energy，2014，63:55-68.

［9］ 竺翔明，孙绍述，高明道.摇摆式结构动力分析［J］.水运工程，1984(8):25-30.(ZHU Xiangming，SUN Shaoshu，GAO Mingdao.Dynamic analysis of the pendulum structure［J］.Port＆ Waterway Engineering，1984(8):25-30.(in Chinese))

［10］左其华.海底铰接柱体结构动力反应［J］.大连理工大学学报，1981(S2):105-112.(ZUO Qihua.The dynamic response of an underwater column hinged at the sea bottom under the wave action ［J］.Journal of Dalian University of Technology，1981(S2):105-112.(in Chinese))

［11］ 冯铁城.浮筒的波浪力计算［J］.海洋工程，1996，14(3):36-40.(FENG Tiecheng.Wave exciting forces on floats［J］.The Ocean Engineering，1996，14(3):36-40.(in Chinese))

［12］李继刚，李殿森，杨庆保.从正反两个角度探讨摆式波力电站的吸能机制［J］.海洋技术，1999(1):56-60.(LI Jigang，LI Diansen，YANG Qingbao.Analyzing the energy absorbing law in pendulum wave power station［J］.Ocean Technology，1999(1):56-60.(in Chinese))

［13］FOLLEY M，WHITTAKER T W T，VANT HOFF J.The design of small seabed mounted bottom-hinged wave energy converters［C］//Proceedings of 7th European Wave Tidal Energy Conference.2007.

［14］FOLLEY M，WHITTAKER T J T，HENRY A.The effect of water depth on the performance of a small surging wave energy converter［J］.Ocean Engineering.2007，34:1265-1274.

［15］WHITTAKER T J T，COLLIER D，FOLLEY M，et al.The development of oyster-a shallow water surging wave energy converter［C］//Proceedings of 7th European Wave＆ Tidal Energy Conference.Portugal:［s.n.］，2007.

［16］ HENRY A.The hydrodynamics of small seabed mounted bottom hinged wave energy converters in shallow water［D］.Queen’s University Belfast，2009.

［17］ FLOCARDA F，FINNIGAN T D.Increasing power capture of a wave energy device by inertia adjustment［J］.Applied Ocean Research，2012，34:126-134.

［18］ ODED G，SOLOMON C S，YIM，et al.Analysis of nonlinear response of an articulated tower［J］.International Journal of Offshore and Polar Engineering，1999，2(1):61-66.

［19］ Aquamarine power-wave energy company，developer of Oyster［ED/OL］.2014-10-28，http://www.aquamarinepower.com.

［20］ About waveRoller［ED/OL］.2014-10-28，http://aw-energy.com.

［21］ FALNES J，BUDAL K.Wave-power conversion by power absorbers［J］.Norweg Mar Res，1978，6:2-11.

［22］ NAIKO S，NAKAMURA S.Wave energy absorption in irregular waves by feed forward control system［J］.Hydrodynamics of Ocean Wave Energy Utilization，1986:269-280.

［23］ HOSKIN R E，COUNT B M，NICHOLS N K，et al.Phase control for the oscillating water column［J］.Hydrodynamics of Ocean Wave Energy Utilization，1986:257-268.

［24］ HOSKIN R E，NICHOLS R K.Optimal strategies for phase control of wave energy devices［C］//Proceedings of International Symposium on Utilization of Ocean Waves La Jolla.1986:184-199.

［25］ KORDE U A.Phase control of fl oating bodies from an on-board reference［J］.Applied Ocean Research，2001，23:251-262.

［26］ FALNES J.Optimum control of oscillation of wave-energy converters［J］.Int J Offshore Polar Eng，2002，12:147-155.

［27］ JOURNéE J M J.Theoretical manual of SEAWAY，Release 4.18［R］.Ship Hydrodynamic Laboratory，Delft of Technology，The Netherlands，2000.

［28］王冬姣，邱守强，叶家玮.梯形摆式波能转换装置水动力性能研究［J］.太阳能学报，2014，35(4):589-593.(WANG Dongjiao，QIU Shouqiang，YE Jiawei.Hydrodynamic performance of trapezoidal pendulum wave energy converter［J］.Acta Energiae Solaris Sinica，2014，35(4):589-593.(in Chinese))