全驱动船舶轨迹跟踪初始位置影响分析
邱荷珍,王 磊
(上海交通大学海洋工程国家重点实验室高新船舶与深海开发装备协同创新中心,上海 200240)
船舶轨迹跟踪(dynamic tracking)属于广义上的船舶动力定位,跟动力定位一样,其跟踪成本不随水深而增加。研究轨迹跟踪目的就是希望船舶能够按照操纵者的意愿或者设定的轨迹路线运动,从而能实现作业安全性和效益最大化。轨迹跟踪更具体来说是船舶在规定的时间内,到达原本设定的位置上。挖泥船、拖曳船、铺管船和风电安装船等海洋工程工作船在各自作业时需要保持在一定的位置上,或者要按照预先设定的轨迹精确地移动。具备动力定位能力的船舶在全方位上都会有足够的推进力来进行准确的定位和位置跟踪。
鉴于船舶运动方程的非线性,一些学者利用反步法和李雅普诺夫理论解决船舶轨迹跟踪问题。挪威的Husa等[1]研究非线性路径点跟踪,设定的轨迹既有直线也有圆弧线,基于反步法设计一种平稳的非线性控制律,避免了直线和圆弧的转折问题,通过积分作用来补偿船舶所受到的低频风流和一阶波浪力。Fossen等[2]对船舶全局指数跟踪研究中利用非线性矢量反步法,对船舶的水平位置(x,y)和艏摇(ψ)同时进行全局指数跟踪,通过非线性控制理论解决运动方程、科氏向心力以及水动力阻尼力的非线性部分,对一艘非线性的供给船进行数值仿真,验证该控制律的控制效果。Godhavn等[3]提出基于非线性反步法和自适应反步法进行全驱动船舶轨迹跟踪的设计。非线性反步法是设计船舶轨迹控制系统的常用方法,但要依赖于船舶匀速与仅受波浪作用的假设;而自适应反步法则主要是用来避免控制系统设计中出现非对称惯性矩阵,即船舶在时变的风流和波浪二阶力等外环境力中也可以有较好的轨迹跟踪效果。Pettersen等[4]对于非线性船舶的输出反馈跟踪定位采用合成的观测器与控制器使得闭环系统达到半全局指数稳定,对于特殊的目标轨迹即定常的位置和航向角且船舶模型忽略科氏向心力的作用,那么该系统可以达到全局指数稳定。同时,偏差的测量对保证其闭环系统具有半全局指数稳定具有决定性的影响。船舶的非线性模型采用Fossen[5]所用模型,而且研究运用了数值仿真的研究手段。Breivik等[6]对比了轨迹跟踪方案中两个运动控制的概念:伺服运动控制和引导运动控制。伺服运动控制是动力定位里面的常用方法,易于推导和分析,但是不便扩展于欠驱动船舶上;而引导运动控制来自于导弹制导,路径跟踪和编队控制的一个新概念,其推导和分析较伺服运动控制复杂,但其易于扩展到欠驱动船,并且具有缓和的收敛行为。
葡萄牙的Encarnaçao等[7]将无人船的轨迹跟踪和航迹跟踪放在一起综合考虑,在航迹跟踪的同时可以得到良好的轨迹跟踪性能,提出同时实现两者的控制方法,并用其仿真一艘船在沿着设定的航迹运动,而另一艘船则紧跟其后进行轨迹跟踪,结果显示轨迹跟踪误差小。新加坡的Tee等[8]提出在基于前馈近似的思想进行全驱动船舶的轨迹跟踪控制。未知外界干扰条件的情况下,近似估计方法和控制设计技术的结合使得能够估计外部条件变化。全状态反馈(full-state feedback)控制,主要基于反步法和李雅普诺夫理论;输出反馈(output feedback)控制,则主要采用高增益观测器来估计不可测的状态。美国的Lee等[9-10]认为水面船舶只考虑三自由度的轨迹跟踪控制不能忽略附加质量的影响,但考虑附加质量会使惯性矩阵成为非对称矩阵,故用一个上三角矩阵前乘惯性矩阵使非对称转化为对称的,对轨迹跟踪提出全状态反馈控制器和输出反馈控制器。随后,引用Chen等[11]的自适应全状态反馈控制及自适应输出反馈控制这两种方法,提出基于工程即时估计参数的方法来估计未知的动态参数。数值模拟的结果显示两个控制方法在不稳定参数下得到最终一致有界的轨迹跟踪。
国内的Cheng等[12]对考虑水平面非线性运动的船舶提出多变量滑模控制方法,利用李雅普诺夫理论证明该控制方法是稳定的,对Fossen[5]所介绍的供给船模型进行数值仿真,检验其控制方法是可用的。Yang等[13]提出一种基于干扰观测器、反步法和李雅普诺夫直接方法,能在未知的随时间变化的环境干扰下的控制器,而且全驱动船模CyberShip II的非线性运动模型有考虑科氏向心力和非线性阻尼等。数值模拟后看出其控制方法可以使船舶轨迹跟踪的闭环系统全局统一并有界,从而实现预设的目标轨迹跟踪。Zhang等[14]对一艘高速船的轨迹跟踪提出基于神经网络反馈前馈补偿器的自适应输出反馈控制器。在高速船的轨迹跟踪中,非线性水动力阻尼不易测量,故采用神经网络反馈前馈补偿器作为一种未知部分来补偿;同样地,利用李雅普诺夫理论给出稳定分析,证明其控制方法可以保证闭环系统中信号是全局统一并有界;数值仿真结果表明其控制方法对轨迹跟踪的效果非常出色。
以上普遍都是用理论分析和数值计算的方法对船舶轨迹跟踪进行研究,而模型试验应用也已实现。挪威的Wondergem等[15-16]提出了只考虑位置和航向的输出反馈跟踪控制,还提出了观测器-控制器组合。考虑了包括科氏力、向心力和非线性阻尼在内的船舶完整动力学,得到半局一致稳定闭环系统。除了理论分析及数值仿真外,还对全驱动船模CyberShip II进行模型试验,从模型试验的过程和结果更能反映模型能够基本实现轨迹跟踪。其后在其硕士论文中详细分析了全驱动船舶轨迹跟踪的输出前馈控制方法,讨论了只有位置测量值时、同时有位置测量值和艏摇测量值的跟踪观测器的设置以及其运行效果。Keizer等[17]根据挖泥船作业特点设计一套挖泥船动力定位轨迹跟踪系统,即DPDT系统,在不同作业阶段时选择动力定位模式或者轨迹跟踪模式,以提高作业精度。
以一艘全驱动船为研究对象,在给定的环境载荷条件下,对船舶进行预设轨迹分别为直线和曲线的轨迹跟踪时域模拟,通过分析船舶时域模拟轨迹与预设轨迹的水平偏差与艏向角偏差来研究轨迹跟踪精度,并分析船舶初始位置对轨迹跟踪精度的影响,为船舶轨迹跟踪的模型试验或者对实船轨迹跟踪的轨迹预设提供参考。
1 理论介绍
1.1 坐标系
为了描述船舶的运动,建立两套坐标系,一个是大地坐标系xEoEyE,一个是船体坐标系xbobyb,两个坐标系z轴都向上。船体坐标系原点在船舶重心,如图1所示。
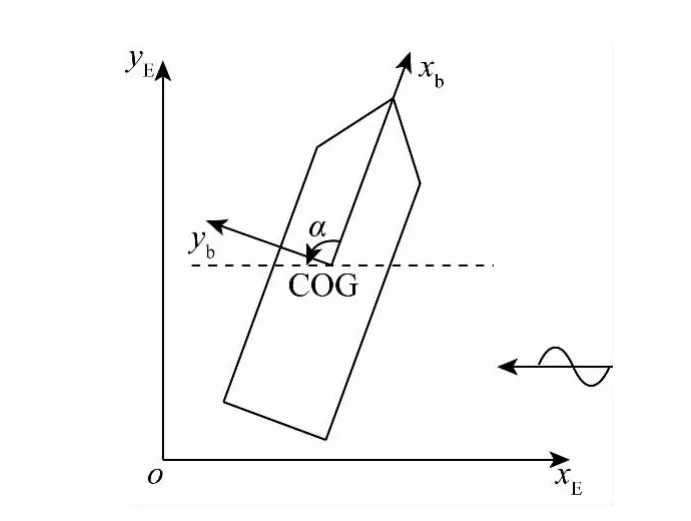
图1 坐标系的定义Fig.1 Definition of coordinate frames
船舶在大地坐标系中的位置及艏向角用向量η= [ x y ψ]T表示,船舶在船体坐标系中的纵荡、横荡和艏摇的速度用向量v= [ μ ν γ]T表示。船舶在大地坐标系下的线性速度与船体坐标系下的速度通过坐标转换矩阵联系起来。转换矩阵为[18]

1.2 运动方程
船舶在风浪流的外载荷作用下引起运动响应,通常风载荷和流载荷变化较为缓慢,可处理为准静态的外载荷,而波浪的作用成分比较复杂。一阶波浪力使船舶在其平衡位置产生波频运动,而平均漂移力会使船舶偏离其平衡位置。船舶轨迹跟踪系统只考虑船舶的低频运动。船舶在外力作用下的低频运动方程为[18]:
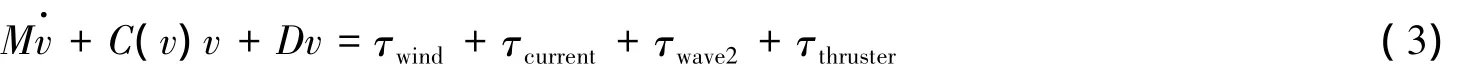
式中:M是包含附加质量的惯性矩阵,ν是船舶的速度向量,C(v)是科氏力和向心力矩阵,D是阻尼矩阵;τwind是风力,τcurrent是流力,τwave2是低频波浪力,τthruster是推力器产生的推力。
风载荷的计算表达式:

式中:ρa是空气的密度;Cwx(γw),Cwy(γw)和Cwψ(γw)分别是在纵向、横向和首摇方向的无因次风力系数;Awx,Awy分别为船舶在纵向和横向的受风面积;Loa为船舶总长,Lxz和Lyz分别是纵向和横向的风力作用点距重心的距离;Vw为海平面以上10 m处的相对风速;γw是风向与船舶x轴正向的夹角。
考虑水平面内的运动,用于时域模拟的风力计算可直接取为

获得风力系数最精确的方法是对船舶进行风洞试验,然而风洞试验费用昂贵,一般采用经验公式的方法估算。这里风载荷计算采用模块法,也是DNV和ABS船级社建议采用的方法[19]。
类似风力计算,作用在船舶上的流力和力矩可以表示为:
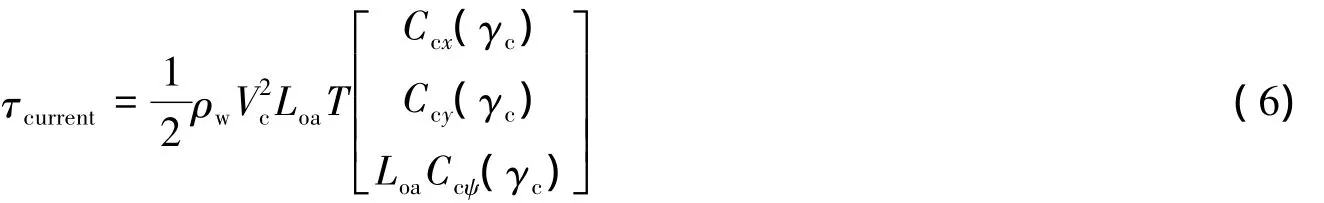
式中:ρw是海水密度;Ccx(γc),Ccy(γc)和Ccψ(γc)分别为纵向、横向和首摇流力系数;Vc为流速大小;Loa为船舶总长;T为船平均吃水。
二阶波浪力包括平均漂移力、低频(差频)力和高频(和频)力三个部分,与入射波的平方成正比,可以用二次传递函数(QTF)来表示。
假定入射的不规则波用谐波的叠加来表示,则二阶波浪力(忽略和频部分)可以表示为:

式中:ωi是波浪频率,ζi是波幅,εi是随机相位角,Pij和Qij就是二次传递函数。
文中仅考虑平均漂移力,如下式所示:

式中:Sζ(ω)为波浪谱密度,P(ω,ω)为二阶传递函数的同相位矩阵,ω为波浪频率。
推力器的总推力为各个推进器的总和。对于每个推进器的推力计算,由模型试验和理论方法计算推力器的敞水性能参数,代入式(9)中计算得到。

式中:n为螺旋桨转速;Q为螺旋桨转矩;D为螺旋桨直径;KT为推力系数;KQ为转矩系数,可根据轴向进速在螺旋桨敞水性能曲线上查取。
1.3 推力分配
推力分配是按照功率最优的原则将控制器计算出来的总推力分配到各个推力器上。通过求解如下最优化问题的最小值的解来获得推力分配的结果[20]:
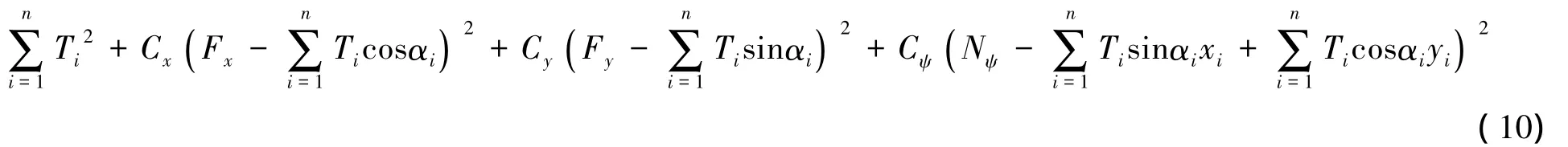
其中,Ti是第i个推力器的推力,n是推力器的数目,C是权重系数,αi是推力器的方向,xi和yi是推力器相对于船舶重心的位置。同时,可以通过设置禁止角即对αi的取值范围加以限制来减小推力器之间的水动力干扰。
1.4 时域模拟原理
船舶轨迹跟踪的时域模拟是对船舶轨迹跟踪真实运动进行实时模拟,对运动状态进行时域模拟能考虑到更多的因素和限制条件,从而能更接近实际情况,同时取得许多有价值的信息,如轨迹跟踪精度、功率消耗等。船舶轨迹跟踪模拟的流程如图2所示,主要模块包括风浪流环境力的计算模型、控制系统模型、推力系统模型以及船舶运动方程等[21]。
2 时域模拟算例
2.1 船舶参数
以一艘近海工程安装船为例,其主尺度:总长(L)为130 m,垂线间长(LPP)为124 m,型宽(B)为40 m,型深(D)为9 m,吃水(H)为5.8 m;组成部分包括船体、艏楼、液压桩腿、起重吊机、直升机甲板等;配备等级为DP-2动力定位系统。
2.2 推力器系统布置
本次计算中船舶推力系统配置三套全回转推进器(3×3 500 kW)和两套艏侧推器(2×2 000 kW)。其中全回转推力器选用额定功率为3 500 kW的系数Ka4-70 19A导管桨,其禁止角设为30°。推力器分布如图3所示。其中,设定全回转推进器朝向船首为180°,船尾为0°,逆时针旋转;1号推力器禁止角设为75°~105°,2号推力器禁止角为255°~285°。禁止角(forbidden angle)是指推进器推力的矢量方向所禁止进入的角度范围,目的是避免其中一个推进器的尾流对另一推进器水动力性能的显著干扰。在推力分配策略中,禁止角通常被视为一个固定的设置,为增大推力角的可行区间,提出动态禁止区间的概念[22]。
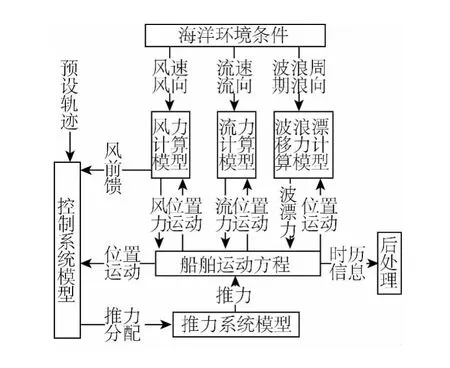
图2 船舶轨迹跟踪时域模拟流程Fig.2 Model of motion simulation for DT

图3 推力器布置示意Fig.3 Arrangement of the thrusters model
2.3 海洋环境条件
该船舶工作环境条件为风速15 m/s,流速为1.03 m/s,采用JONSWAP谱,有义波高为2 m,谱峰周期为8.12 s。由于风、浪、流同向作用时为最恶劣的环境条件,故取风、浪、流同向联合作用作为计算的环境条件。模拟环境载荷作用方向取为大地坐标系xEoEyE的x轴反向,即180°,如图1所示。计算水深取为50 m,且假定所有推力器完好。
2.4 预设轨迹
预设直线轨迹起始点为(0,0),取y=x,设定船速为v=0.5 m/s。曲线轨迹为起点为(0,0),半径400 m,圆心在(400,0)处的圆,设定船舶运动的航速是v=0.5 m/s。
3 结果与分析
3.1 轨迹跟踪精度
利用MARIN开发的软件DPSIM,对船舶跟踪预设轨迹进行时域模拟。文中对直线轨迹的模拟时间为2 500 s,对圆轨迹的模拟时间为3 660 s,记录数据步长为20 s。时域模拟过程中,需要设置轨迹跟踪的控制精度。控制精度(Δx,Δy,Δψ)指的是船舶当前位置和目标位置的最大水平偏差和艏向角偏差。通过减小轨迹跟踪的控制精度,使得船舶偏离设定轨迹,从而得到设定速度下的最高精度。直线轨迹的控制精度为(5,5,3°)、(4,4,3°)、(3,3,3°)和(2,2,2°);圆轨迹的控制精度为(10,10,5°)、(5,5,5°)、(4,4,4°)和(4,4,3°)。
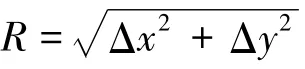
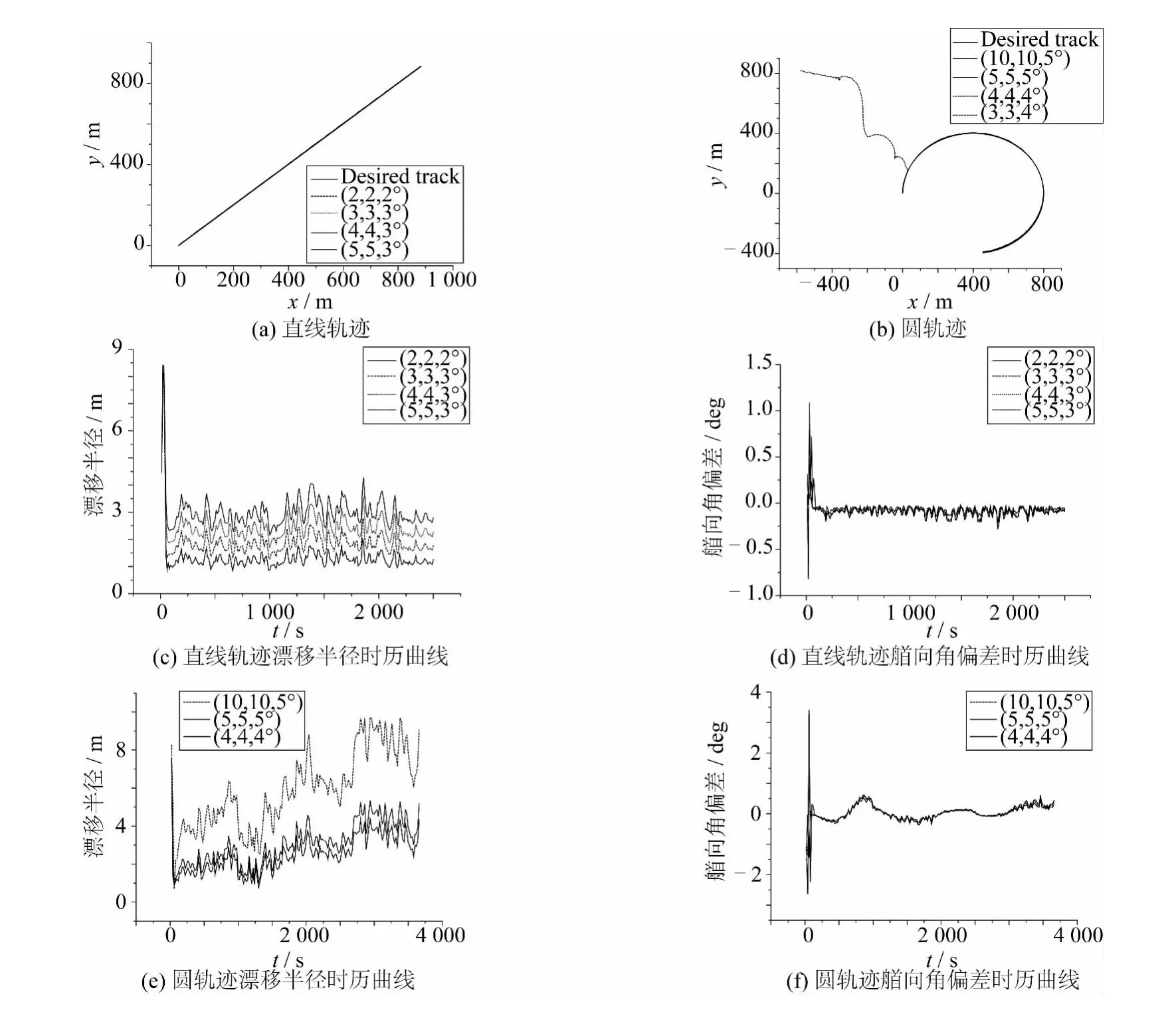
图5 不同控制精度下轨迹和各参数时历曲线Fig.5 Track and time trace under different control precisions
3.2 船舶初始位置对轨迹跟踪影响
船舶初始位置指船舶出发的水平位置和艏向(x,y,ψ)。根据预设直线,船舶的初始位置应为(0,0,45°)。
计算中船舶初始水平位置为(0,-5,45°)、(-5,0,45°)、(0,5,45°)、(5,0,45°)、(0,10,45°)、(0,15,45°)、(0,20,45°)和(0,30,45°)。图 6(a)为轨迹跟踪图,尽管初始出发点不同,船舶依然能够进行轨迹跟踪,但需要逐渐调整位置。如图6(b)所示,初始水平位置偏离越大,则调整至目标位置所需的距离和时间越长。图6(c)为漂移半径时历曲线,水平位置偏离(0,30,45°)时船舶调整时间大约为100 s,各个初始位置在100 s后轨迹跟踪漂移半径曲线几乎重合。图6(d)为艏向角偏差时历曲线,初始位置为(0,20,45°)时出现最大首摇角。
进行轨迹跟踪时,初始水平位置偏差对首摇影响不太,但初始艏向偏离对横荡和纵荡位置影响较大,严重时导致偏离预设轨迹。计算中船舶初始艏向角分别为(0,0,40°)、(0,0,45°)、(0,0,50°)、(0,0,59°)和(0,0,60°)。各跟踪轨迹和参数时历曲线如图7所示。
从图7(a)看出,艏向为45°~59°时,模拟轨迹与预设轨迹几乎重合,但当艏向为60°时,模拟轨迹和预设轨迹完全分离,说明初始艏向角偏离过大,会引起轨迹跟踪失败。图7(c)和(d)中初始艏向偏差没有超过15°时,漂移半径和艏向角偏差时历曲线重合很好,说明在偏差允许范围内,初始艏向偏差对跟踪精度影响甚微,但超出允许范围后,会导致轨迹跟踪失败。

图6 不同初始水平位置下的轨迹和参数时历曲线Fig.6 Track and time trace under different start horizontal positions

图7 不同初始艏向下的轨迹和参数时历曲线Fig.7 Track and time trace under different start headings
4 结语
1)船舶考虑风浪流外载荷作用下进行轨迹跟踪时域模拟,相同速度下直线轨迹跟踪精度比圆轨迹跟踪精度高。
2)船舶初始水平位置对轨迹跟踪初期效果影响较大。由于有初始位置偏差,船舶需要一个调整阶段,逐渐跟上预设轨迹。初始位置偏离越大,船舶调整周期越长。对于实际工程中,应避免船舶初始水平位置偏离过大。
3)轨迹跟踪时,船舶初始艏向偏差存在一个允许范围。艏向偏差在范围内,对轨迹跟踪效果没影响,但一旦超出这个范围,在限定的时间内,会导致轨迹跟踪失败。因此先利用动力定位系统将船舶调整至船舶最佳的初始位置,然后开始轨迹跟踪。
[1] HUSA K E,FOSSEN T I.Backstepping designs for nonlinear way-point tracking of ships[J].Manoeuvring and Control of Marine Craft,1997.
[2] FOSSEN T I,BERGE S P.Nonlinear vectorial backstepping design for global exponential tracking of marine vessels in the presence of actuator dynamics[C]//Proceedings of the 36th IEEE Conference on Decision and Control.1997:4237-4242.
[3] GODHAVN J,FOSSEN T I,BERGE S.Non-linear and adaptive backstepping designs for tracking control of ships [J].International Journal of Adaptive Control and Signal Processing,1998,12(8):649-670.
[4] PETTERSEN K,NIJMEIJER H.Output feedback tracking control for ships[J].New Directions in Nonlinear Observer Design,1999:311-334.
[5] FOSSEN T I.Guidance and control of ocean vehicles[M].John Wiley& Sons,1994.
[6] BREIVIK M,FOSSEN T I.A unified concept for controlling a marine surface vessel through the entire speed envelope[C]//Proceedings of the IEEE International Symposium on Intelligent Control,Mediterrean Conference on Control and Automation.2005:1518-1523.
[7] ENCARNAçAO P,PASCOAL A.Combined trajectory tracking and path following:an application to the coordinated control of autonomous marine craft[C]//Proceedings of the 40th IEEE Conference on Decision and Control.2001:964-969.
[8] TEE K P,GE S S.Control of fully actuated ocean surface vessels using a class of feedforward approximators[J].Control Systems Technology,IEEE Transactions on,2006,14(4):750-756.
[9] LEE D B,TATLICIOUGLU E,BURG T C,et al.Robust output tracking control of a surface vessel[C]//American Control Conference.2008:544-549.
[10] LEE D B,TATLICIOGLU E,BURG T C,et al.Adaptive output tracking control of a surface vessel[C]//Proceedings of the 47th IEEE Conference on Decision and Control.2008:1352-1357.
[11] CHEN J,BEHAL A,DAWSON D M.Adaptive output feedback control for a class of MIMO nonlinear systems[C]//Proceedings of the American Control Conference.Minneapolis:[s.n.],2006:5300-5305.
[12] CHENG J,YI J,ZHAO D.Design of a sliding mode controller for trajectory tracking problem of marine vessels[J].IET Control Theory& Applications,2007,1(1):233.
[13] YANG Y,JIALU D,CHEN G,et al.Trajectory tracking control of nonlinear full actuated ship with disturbances[C]//Proceedings of International Conference of Soft Computing and Pattern Recognition(SoCPaR).2011:318-323.
[14] ZHANG L J,JIA H M,QI X.NNFFC-adaptive output feedback trajectory tracking control for a surface ship at high speed[J].Ocean Engineering,2011,38(13):1430-1438.
[15] WONDERGEM M,LEFEBER E,PETTERSEN K Y,et al.Output feedback tracking of ships[J].Control Systems Technology,IEEE Transactions on,2011,19(2):442-448.
[16] WONDERGEM M.Output feedback tracking of a fully actuated ship[D].M.Sc.thesis,Dept.Eng.Eindhoven Univ.Technol.,Eindhoven.The Netherlands,2005.
[17] KEIZER C D,KLUGT P V D.A new generation DpDt system for dredging vessels[C]//Dynamic Positioning Conference.2000.
[18] FOSSEN T I.Handbook of marine craft hydrodynamics and motion control[M].John Wiley& Sons,2011.
[19]王先福,杨建民,王磊.海上浮体动力定位外力计算[J].海洋工程,2005,23(3):45-50.(WANG Xianfu,YANG Jianmin,WANG Lei.Study on the disturbing forces for dynamic positioning system of ocean floating structures[J].The Ocean Engineering,2005,23(3):45-50.(in Chinese))
[20] Marin dpsim user guide[S].
[21]杨欢,王磊,申辉.深水半潜式钻井平台动力定位实时功率模拟研究[J].海洋工程,2012,30(2):14-19.(YANG Huan,WANG Lei,SHEN Hui.Research on real-time power simulation of dynamic positioning based on a deep sea semi-submersible drilling platform[J].The Ocean Engineering,2012,30(2):14-19.(in Chinese))
[22]李博.动力定位系统的环境力前馈研究[D].上海:上海交通大学,2013.(LI Bo.Study on environmental loads feed-forward of dynamic positioning system[D].Shanghai:Shanghai Jiao Tong University,2013.(in Chinese))

