基于相当故障树的海洋石油平台动力系统测试诊断策略研究
余 平,张裕芳,易 宏,王鸿东
(上海交通大学海洋工程国家重点实验室,上海 200240)
如今,海洋石油平台系统越来越复杂,再加上海上恶劣的工作环境,导致系统发生故障或失效的潜在可能性也逐渐增大,因故障导致的维修将造成巨大的经济损失或环境灾难事故。出于对安全保障和经济效益的考虑,通过布置测试设备及时准确和动态地确定各系统的运行状态从而实现预防性维修,通过制定故障诊断策略实现快速定位故障从而指导维修工作,对于海洋石油平台系统而言具有重要的实际意义,这也是海洋石油平台进行故障诊断和测试性工作的重要内容和目标。
目前开展的故障诊断与测试性工作主要集中在电子设备方面[1-3],对于像海洋石油平台这种由机电液等多类设备组成的复杂机械系统的测试性工作还少有研究。另一方面,由于海洋石油平台系统复杂、设备繁多,再加上故障原因复杂,故障诊断工作主要集中在各设备或零部件层面,并未以系统为出发点来制定诊断策略。
对海洋石油平台做到系统全局的故障诊断以及测试性工作难度太大,但是可以通过制定故障诊断策略来实现快速地将故障隔离到设备或组件等可更换单元上。类似的研究工作已经开展不少。例如,Pattipati等[4]提出了一种动态规划算法运用于搜寻最优诊断策略;Deb等[5]介绍了多信号流图模型运用于测试性分析和故障诊断;Zhu等[6]则运用贝叶斯网络优化电力系统故障诊断策略;连光耀等[7]针对复杂电子系统依据故障隔离权值找到最优故障隔离节点,通过节点的信息量确定最佳测试点和最优故障诊断策略;倪绍徐等[8]以船舶电力系统为例,基于故障树计算出单元关键重要度并结合平均故障检测时间,以此为依据确定故障诊断的最优程序。另一方面,可以在故障分析的基础上,合理地优化测试点布置方案,为测试设备安装提供依据。这部分工作主要是根据故障信息和测试费用等因素进行测试点的优选,Shi等[9]通过综合测试性度量、故障概率和测试费用等因素,针对航空电子系统提出了一种系统级优选测试点方法和两种诊断策略(包括最少测试步骤及节约测试费用)。
本文将在故障模式、影响和危害性分析(failure mode,effects and criticality analysis,FMECA)与FTA(fault tree analysis)的基础上建立相当故障树模型,计算最小割集重要度,并据此设置测试点以及建立最小割集诊断策略。再根据单元故障的关键重要度、测试费用和平均故障检测时间(mean time to detection,MTTD)三者信息确定最小割集内底事件诊断策略。
1 基于相当故障树的测试诊断策略
1.1 相当故障树模型
在FMECA分析的基础上,可以建立故障树模型。考虑到海洋石油平台系统复杂的特性,所建故障树过于庞大,因此有必要简化故障树给测试诊断工作带来方便。假设通过FTA分析求得故障树共有K个最小割集,则故障树的结构函数ψ(x)可表示为:

式中:Gk(x)表示第k(1≤k≤K)个最小割集,假设第k个最小割集内有M个单元,xi(1≤i≤M)表示为割集所对应的底事件向量。这样就可以将故障树等效地转化成用最小割集来表示[10]。其中最小割集内的各个底事件之间是“与”的关系,而各个最小割集之间是“或”的关系,进而故障树可以转化成如图1所示的相当故障树。从图1可以看出,可以将复杂的系统失效故障树转化为只有三级(顶事件层、最小割集层和最小割集内底事件层)的相当故障树。这样一来就大大简化故障树模型,并且可以清晰地指导系统故障测试与诊断工作。
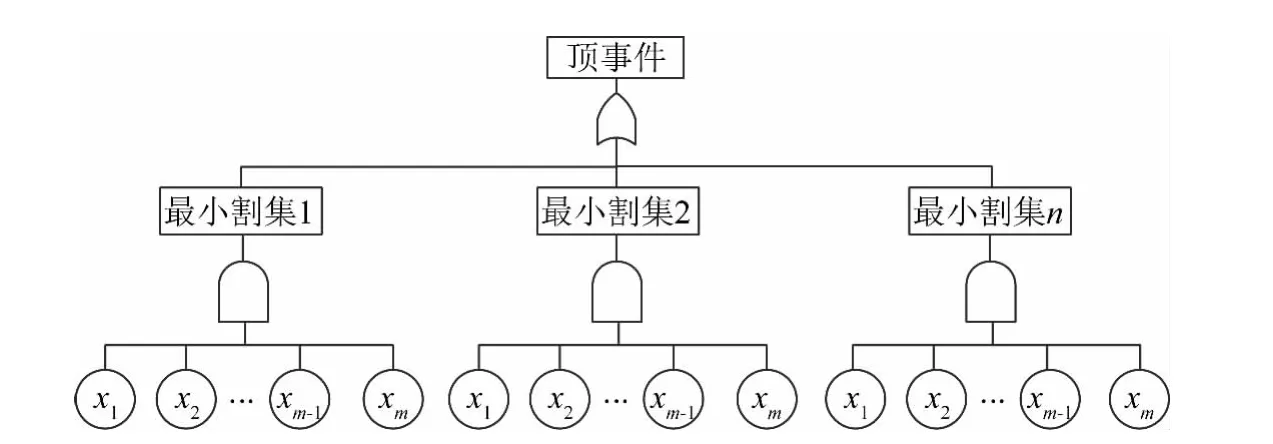
图1 相当故障树模型Fig.1 Model of equivalent fault tree
1.2 布置测试点和建立诊断策略
从如图1所示的相当故障树模型可知,在对系统进行布置测试点和建立故障诊断策略工作时,需要分别从最小割集层和底事件层展开。由单元关键重要度概念可知[11],单元对系统发生故障的贡献程度(即关键重要度)越大,则该单元故障引发的系统故障的可能性越大。

由此引入最小割集关键重要度:
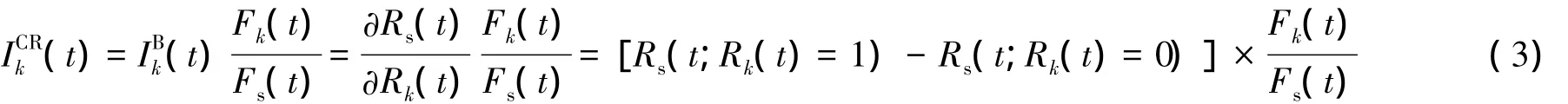
由最小割集的定义可知,最小割集一旦发生,顶事件就发生。当最小割集内底事件全部发生,最小割集才发生。所以有:
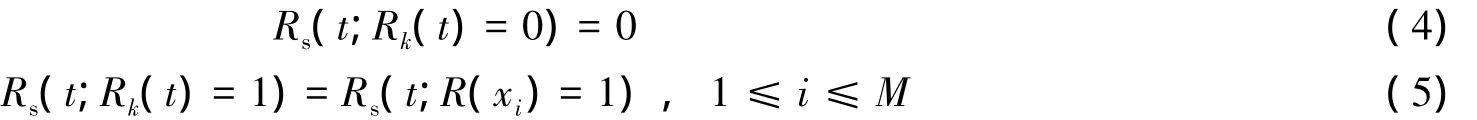
将式(4)、(5)代入式(3),得:

通过Mont-Carlo方法对底事件失效进行抽样仿真。假设设第i个单元xi失效时间抽样值为[12]:ti=(ξ)。其中,ξ为[0,1]之间均匀分布的随机数(ξ)为第i个单元失效时间的分布函数,则时间t下第i个单元的不可靠度为Fi(t)。当M个单元都失效时,该最小割集就发生了,因此,第k个最小割集的发生时间为:

假设共进行Ns次仿真,则第j(1≤j≤Ns)次仿真系统失效时间tj即最先发生的最小割集的时间:
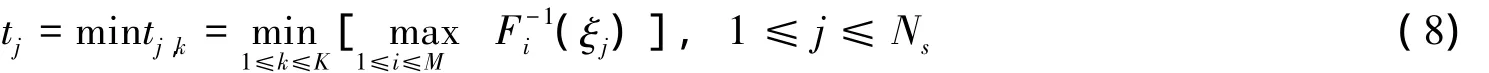
记系统运行时间为t,则时间t下第k个最小割集的不可靠度为:

设φ(tj)是一个状态变量,其值定义如下:

则在Ns仿真情况下,累计系统失效时间tj小于系统运行时间t的次数,则系统不可靠度可表示为:




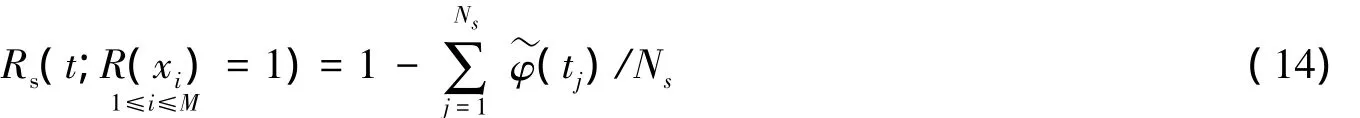
则式(6)变成:


考量指标Qi越大,则说明越应该布置测试点。由此,便确定了系统测试点的布置策略。
2 实例分析
2.1 埕岛中心一号海洋石油动力平台电力系统简介
以胜利油田埕岛中心一号海洋石油动力平台电力系统进行实例分析。海上卫星平台生产的原油输送到埕岛中心一号平台储罐中以后,进行油气分离,分离出的天然气再经由管道,到达1#、2#天然气洗涤器进行净化,并且控制在一定的压力、温度和流量,便成为符合燃烧标准的燃料气,供给发电机组用于发电(如图2所示)。发电系统主要包括两台半人马座40型燃气轮发电机组、天然气压缩机和热煤加热炉,以及五台190T型燃气轮机发电机组。190T型燃气轮机发电机组作为半人马座40型燃气轮发电机的动力起动机,并作备用发电系统。

图2 埕岛中心一号海上石油平台动力系统示意Fig.2 Operation diagram of the Chengdao Center's NO.1 offshore oil platform power system
2.2 海洋石油动力平台电力系统相当故障树模型
在对海洋石油平台动力系统的设计资料,功能原理图,以及系统启动、运行、控制、维护等有关资料分析的基础上,进行FMECA分析,找到导致动力系统失效的潜在故障模式,并逐级建立系统失效的故障树模型。再根据Fussell算法[13]搜寻最小割集,进而可以建立海洋石油平台动力系统失效的相当故障树模型。限于篇幅原因,具体的FMECA过程并不给出,图3给出了故障树模型。表1给出了具体的故障树代码说明,M表示中间事件(medial event),B表示底事件(bottom event)。相当故障树模型则在MCS的结果上建立,其模型以图1形式给出,MCS结果则由表2给出。
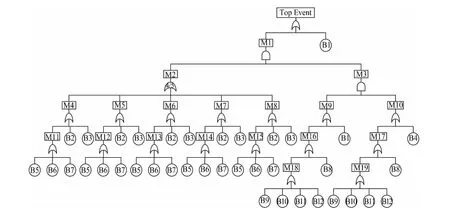
图3 海洋石油平台动力系统失效故障树模型Fig.3 Fault tree model of Chengdao Center's NO.1 offshore oil platform power system

表1 故障树代码说明Tab.1 Codes and description of the events

表2 最小割集重要度排序Tab.2 Order of MCS importance
2.3 仿真结果与分析
采用上述描述的Mont-Carlo仿真方法,对上述相当故障树模型进行分析,具体流程如图4所示。
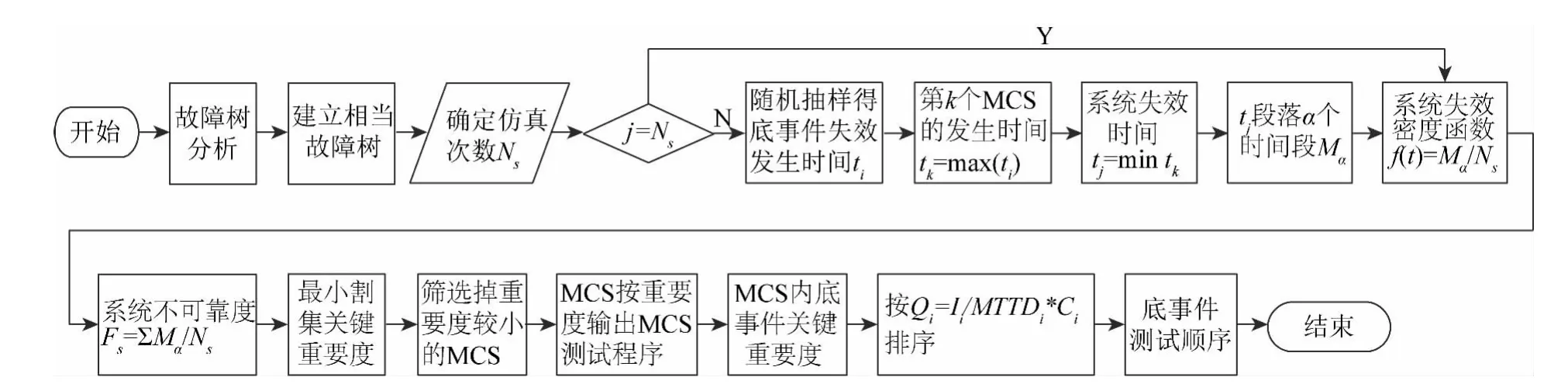
图4 仿真流程Fig.4 Flow chart
根据上述仿真结果,便可建立海洋石油动力平台电力系统的测试诊断策略。在最小割集层次,按照表2所给顺序依此测试,且一旦确定最小割集内某个底事件是正常工作的,便排除含此底事件的最小割集,直接进入下一最小割集的测试程序。在最小割集内底事件层次,底事件按表3所给Pi大小顺序进行测试。
例如,对于MCS2,依此测试B3、B8,一旦检测到B3是正常工作,则可以排除含有B3的各MCS。对于测试点的优化布置,则根据表3所给的Qi大小顺序进行。如在该动力平台电力系统中,首先应该在6 kV的高压配电系统设置测试点,其次是solar配电系统以及190T配电系统。测试方法则根据具体情况而定,可以是BIT(机内测试设备)也可以是ATE(自动测试设备)。
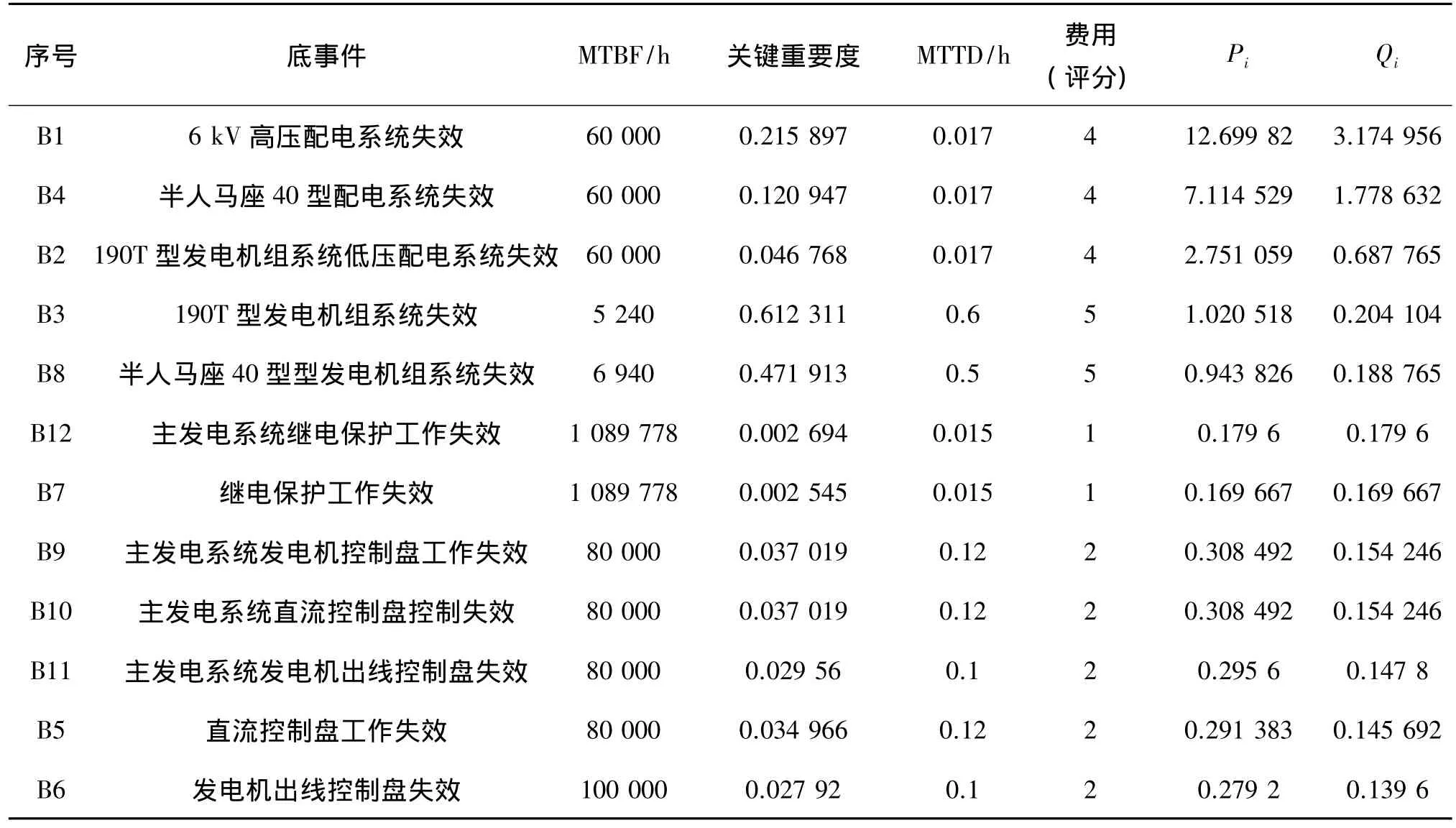
表3 各底事件故障数据及计算结果Tab.3 The fault data and results of each bottom event
3 结语
由于目前海洋石油平台测试性工作刚刚起步,且面临着系统复杂、可维修的难题,还未形成以系统为出发点的测试诊断策略。将复杂的系统简化为只有三级的相当故障树,并定义最小割集关键重要度的概念,筛选出重要度较大的最小割集来制定故障诊断策略。对于最小割集的故障诊断顺序,可以按照最小割集重要度大小顺序展开。对于最小割集内底事件的测试顺序,则综合考量单元关键重要度、平均故障检测时间两方面因素展开。若是最小割集内某底事件诊断结果是正常工作,则排除此最小割集,直接进入下一个最小割集的诊断程序。系统安装在线测试装置时,则需要综合考虑单元关键重要度、平均故障检测时间和测试费用三者因素。最后,以胜利油田埕岛一号海洋石油平台动力平台电力系统为研究对象,以此方法建立测试诊断策略,结果表明本方法不仅能建立系统的诊断策略,还能为系统布置测试设备提供依据,具有实际工程意义。
[1] 田仲,石君友.系统测试性设计分析与验证[M].北京:北京航空航天大学出版社,2003.(TIAN Zhong,SHI Junyou.System testability design analysis and verification[M].Beijing:Beihang University Press,2003.(in Chinese))
[2] WILLIAMS T W,PARKER K P.Design for testability—A survey[J].Proceedings of the IEEE,1983,71(1):98-112.
[3] NAGLE H T,ROT S C,HAWKINS C F,et al.Design for testability and built-in self test:a review[J].Industrial Electronics,IEEE Transactions on,1989,36(2):129-140.
[4] PATTIPATI K R,ALEXANDRIDIS M G.Application of heuristic search and information theory to sequential fault diagnosis[J].Systems,Man and Cybernetics,IEEE Transactions on,1990,20(4):872-887.
[5] DEB S,PATTIPATI K R,RAGHAVAN V,et al.Multi-signal flow graphs:a novel approach for system testability analysis and fault diagnosis[J].Aerospace and Electronic Systems Magazine,IEEE,1995,10(5):14-25.
[6] ZHU Yongli,HUO Limin,LU Jingling.Bayesian networks-based approach for power systems fault diagnosis[J].Power Delivery,IEEE Transactions on,2006,21(2):634-639.
[7] 连光耀,黄考利,赵常亮.复杂电子系统测点与诊断策略的优化方法[J].系统工程与电子技术,2004,26(11):1739-1742.(LIAN Guangyao,HUANG Kaoli,ZHAO Changliang.Efficient algorithm for test-node and diagnosis strategies of a complex electronic system[J].System Engineering and Electronics,2004,26(11):1739-1742.(in Chinese))
[8] 倪绍徐,张裕芳,易宏,等.基于故障树的智能故障诊断方法[J].上海交通大学学报,2008,42(8):1372-1375.(NI Shaoxu,ZHANG Yufang,YI Hong,et al.Intelligent fault diagnosis method based on fault tree[J].Journal of Shanghai Jiao Tong University,2008,42(8):1372-1375.(in Chinese))
[9] SHI Junyou,TIAN Zhong.Efficient algorithm for fault diagnosis strategy[J].Acta Aeronautica Et Astronautica Sinica,2003,24(3):212-215.
[10]易宏.舰船总体可靠性通用模型及舰船可靠性工程方法研究[D].上海:上海交通大学,2003.(YI Hong.Research for warship general reliability model and reliability engineering analysis method[D].Shanghai:Shanghai Jiao Tong University,2003.(in Chinese))
[11] BIRNBAUM Z W.On the importance of different components in a multicomponent system[R].Washington Univ Seattle Lab of Statistical Research,1968.
[12] LIANG X F,YI H,ZHANG Y F,et al.Reliability and safety analysis of an underwater dry maintenance cabin[J].Ocean Engineering,2010,37(2):268-276.
[13] Reliability and fault tree analysis[M].Philadelphia:Siam,1975.

