高桩挡板透空式防波堤消浪性能数值研究
诸裕良,李 雨,陈德春,陶爱峰
(河海大学港口海岸与近海工程学院江苏省海岸带资源开发与安全重点实验室,江苏南京 210098)
透空式防波堤在港口防波挡浪建筑物中颇具发展前景,其消波原理:一方面入水挡板可以反射部分波能;另一方面挡板干扰水体的正常运动,使其在挡板间发生紊动、混掺,以使波能衰减、波高减小,进而使港内达到良好泊稳条件。目前对防波堤消浪性能的研究方法主要有理论分析[1-4]、物模试验[5-8]、现场观测[9]和数值模拟[10-11]。理论分析一般需作简化,与工程实际情况相去较远;物理模型由相似理论按一定比尺缩小,具有直观可见的优点,但是比尺效应难以克服,且成本较大,费时费力;现场观测可得最可靠结果,其观测周期长、监测成本高的缺点也很明显。近年来,数值波浪水槽研究迅速发展,为防波堤消浪性能的数值模拟提供了可能。刘加海等[12]利用Fluent软件,通过设定造波板边界的运动模拟造波机推板的运动,实现了二维规则波的模拟;周勤俊等[13]提出了适用于VOF方法的源造波消波技术,并利用建立的数值波浪水槽对规则波在海堤上的爬高和越浪过程进行模拟;李凌等[14]在动量方程中添加源项的方法发展了黏性流数值造波和消波技术;何军等[15]分析了规则波作用下T型防波堤附近的流场、流线等变化情况;张成兴等[16]将气液两相流看作变密度的单流体,利用UDF在连续方程中添加质量源建立了气幕式防波堤数学模型。
目前高桩透空式防波堤已在多个工程中使用,但对其消浪效果的数值模拟还很少见,因此建立实用的数值波浪水槽分析透空式防波堤消浪效果的影响因素意义重大。采用源项造波理论,利用Fluent中的用户自定义函数(UDF)进行了二次开发,将入射波场对应的源项加入动量方程,建立了二维数值波浪水槽。源项造波理论[17]是将入射波场添加到以RANS方程为控制方程的动量方程中,对空间分布的源函数法进行改进以实现造波和消波,其中控制方程采用有限体积法进行离散,自由表面用VOF法追踪。研究以某高桩透空式防波堤为工程背景,结合物理模型试验对规则波作用下防波堤透浪系数进行了数值模拟,详细分析了防波堤堤前和堤后流态以及挡板相对入水深度对透浪系数的影响。在数值水槽可靠的基础上,详细分析堤顶相对宽度、相对水深、相对波高对透浪系数的影响,在Weigel公式的基础上提出修正公式,修正公式与计算值吻合较好,透浪系数较小时与试验值吻合良好。
1 基本理论
对防波堤断面透浪系数进行研究,以不可压缩黏性流体的RANS方程为控制方程,通过在动量方程添加的源项实现造波和消波,自由表面采用VOF方法进行跟踪。其控制方程为连续方程和不可压缩黏性流体动量方程:

式中:ρ为水的密度,u、v分别为x、y方向的速度分量,μ为水的动黏性系数,g为重力加速度,Sx、Sy为x、y两个方向的附加动量源。源造波理论将数值波浪水槽按功能分区,分区从左至右依次为造波区、前端消波区、工作区、后端消波区,如图1所示。
经过造波和消波后波动场如下:

式中:各分区内的加权函数C是不尽相同的,其中造波区有[C]xmin=1、[C]xmax=0;前端消波区有[C]xmin=0、[C]xmax=1;后端消波区有[C]xmin=1、[C]xmax=0。以上公式中 u、v分别为 x、y方向的速度分量,p为压强,下标m为作用后的流场值,下标c为计算值,下标i为作用前的来波值,C=C(x)为与空间位置有关的光滑过渡的加权函数。利用不考虑黏性的欧拉方程,可以确定各分区对应的源项Sx、Sy,详细推导过程见文献[18]。
2 数值波浪水槽
2.1 数值波浪水槽建立
整个水槽长度425 m,高24 m,造波区长度75 m,前端消波区75 m,工作区200 m,后端消波区75 m。其中,水槽上部为空气,下部为水,坐标原点在最左端水气交界面处,在水气交界处网格需加密处理。数值水槽边界条件设置如表1所示,各边界位置如图1所示。
采用UDF将源项添加到动量方程中,结合Fluent中的Segregated求解器、VOF模型、标准k-ε模型、PISO算法建立数值波浪水槽。
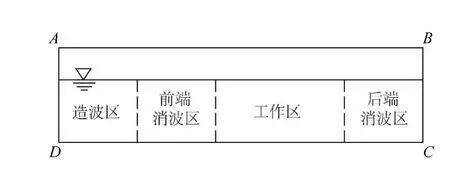
图1 数值水槽示意Fig.1 The sketch of numerical tank

表1 数值水槽边界条件Tab.1 Boundary conditions of the numerical tank
2.2 数值波浪水槽验证
在数值研究前已进行物理模型试验,试验在波浪水槽中进行,造波机为液压推板式造波机,水槽两端设置消浪设备。物理模型制作、试验严格按照波浪模型试验规程,试验采用规则波,模拟波要素分为100年一遇设计波要素、50年一遇设计波要素,具体波要素如表2所示。
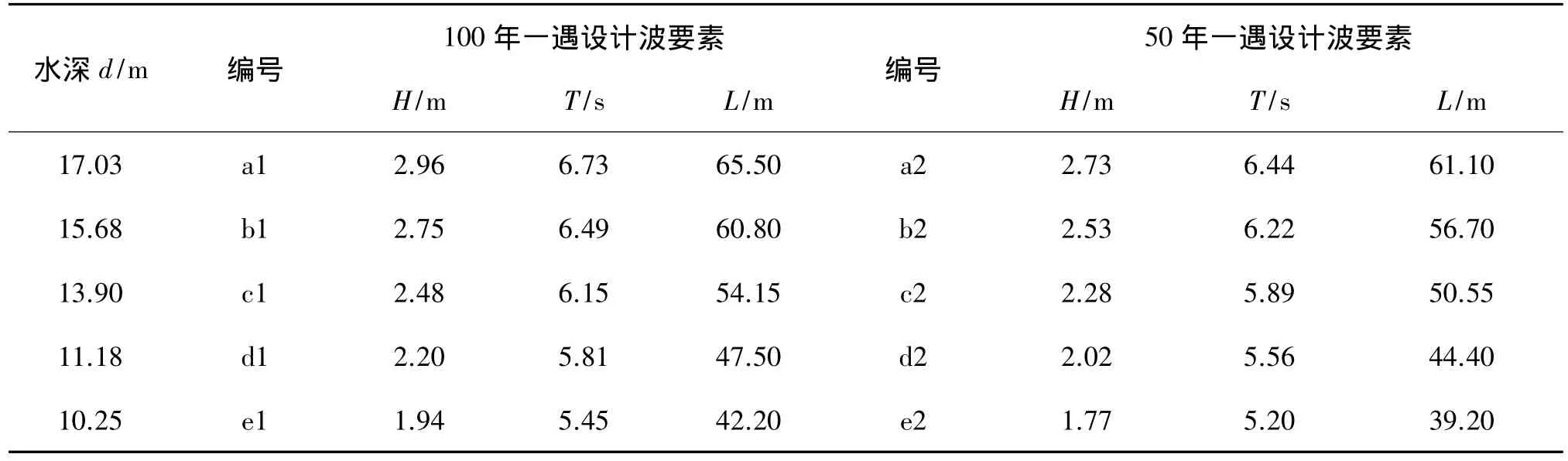
表2 试验波要素Tab.2 Wave elements in experiment
数值模拟同样使用表2中的波要素,在数值监测防波堤透浪状况前,先在未加入防波堤的水槽中造波,检验数值水槽的造波品质。首先模拟a1波要素,监测x=170 m、x=240 m处波面,两处波面时间过程线如图2所示,由图可见,模拟的二阶Stokes波与理论值吻合良好。

图2 两个断面处波面时间过程线Fig.2 Time series of surface elevation at x=170 m and x=240 m
在检验a1波要素后,又对各组次波要素的波高、周期进行了检验,计算后的波高相对误差、周期相对误差如表3所示,从表中看出,数值波浪水槽造波效果良好,波高、周期计算值与目标值相对误差在±5%以内。由波浪模型试验规程[19]可知,建立的数值波浪水槽可以满足透空式防波堤透浪系数研究的精度要求。
3 透浪系数数值研究
3.1 结构型式
防波堤结构型式为高桩挡板透空式,主要结构有置于前后的挡板、纵横梁、面板、两对叉桩、上侧挡浪墙,防波堤断面一示意图,如图3所示。

表3 100年一遇和50年一遇设计波要素计算值与目标值相对误差Tab.3 The relative error between calculated and target values of design wave elements once a hundred years and once fifty years
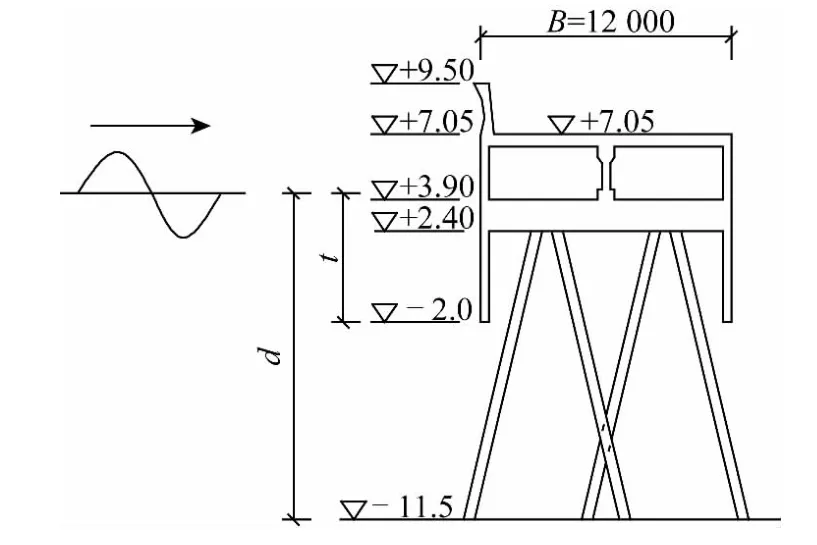
图3 防波堤断面一示意Fig.3 The sectional sketch of breakwater
文中共有三种防波堤断面,以断面一为例,挡浪墙顶高程+9.5 m,前沿底标高-11.5 m,堤顶宽B=12 m、堤顶高程+7.05 m,横梁顶高程+3.9 m、底高程+2.40 m。前后设置挡浪板,挡浪板长度4.4 m,底高程-2.0 m。排架间距为5.0 m,每榀排架布置4根35:1的预应力管桩,管径800 mm,组成2对叉桩。后两个防波堤断面尺寸与第一断面不同点在于:断面二挡浪板底高程为-2.4 m,断面三挡浪板底高程为-3.2 m,其他尺寸与断面一完全相同。在不同水位下,挡板入水深度t是不同的,计算后挡板相对入水深度如表4所示。
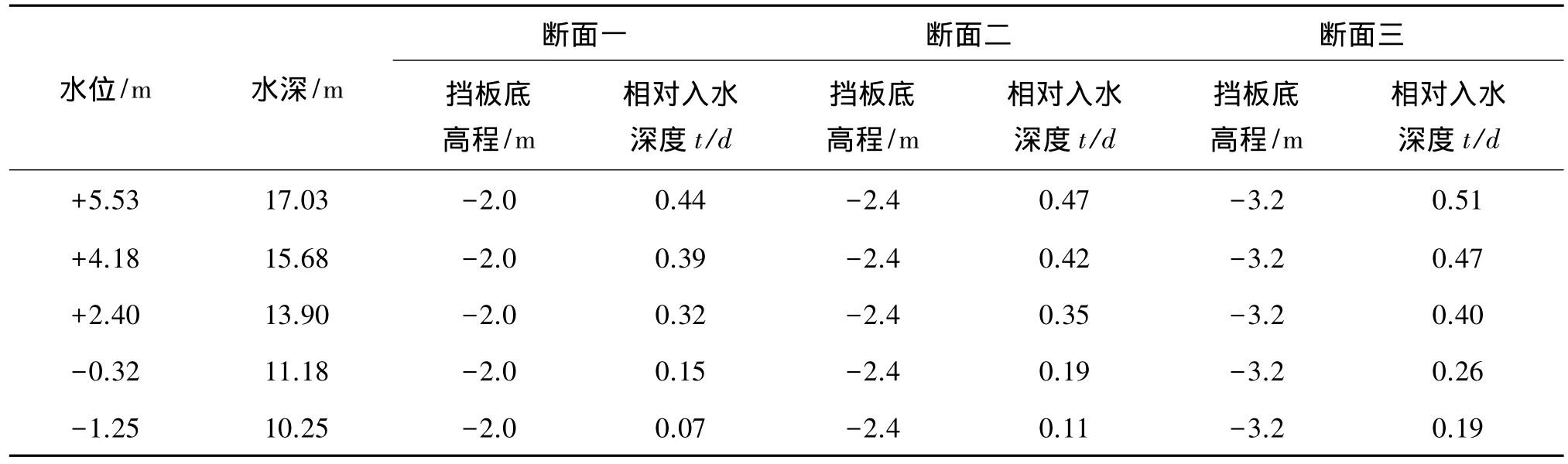
表4 不同水位下挡板相对入水深度Tab.4 The relative immersed depth of barrier at different water levels
3.2 堤前堤后流态
在进行数值模拟时对模型进行了简化,只保留了前后挡板、面板、挡浪墙,其中防波堤前侧挡板横坐标x=200 m。图4为断面三防波堤周围网格加密示意图,为简化网格划分,在横坐标x=195 m至x=217 m范围内,也就是堤前堤后5 m范围内采用非结构化网格;而在其他区域采用结构化网格,这部分网格划分在x方向均是Δx=0.4 m,液面上下一倍波高范围内y方向为均布划分,其中Δy=0.1 m,其余部分的y方向是Δy=0.2 m,总网格数为217 499,最小网格面积为0.002 5 m2。

图4 网格加密示意Fig.4 Sketch of grid refinement
图5为100年一遇a1波要素作用下堤前堤后在t=39~47 s内的速度矢量图和波面图。因为波周期为6.73 s,所以可以完整表现一个周期内堤前后的速度矢量图和波面变化,本例计算的残差图如图6所示,在后续的周期内,速度矢量图和波面图与图5相同,所以可以认定计算已经收敛。

图5 100年一遇波要素a1不同时刻速度矢量图及波面图Fig.5 The velocity vector and wave surface at different moments of design wave elements once in a hundred years

图6 残差图Fig.6 Residuals monitored during iterating
从图5中可以看出,来波遇到前侧挡板阻挡后,上层水体向上运动且速度较大,但并未有越浪发生,这说明挡浪墙的高度是合理的;在堤前波面下落过程中,有相当量的水体发生反射。部分下层水体直接透过防波堤前侧挡板,这部分水体又有部分直接透过后侧挡板;其余水体在两侧挡板间生成较大范围的涡动,形成了涡动消能效应。透过后侧挡板的水体并未有较大的波动,在对各组次的堤后波高监测后发现波高都在1 m以下。
3.3 挡板相对入水深度对透浪系数的影响
在计算了三种断面,五级水位,100年、50年一遇设计波要素共30种组合的透浪系数后,详细分析挡板相对入水深度t/d对透浪系数的影响。各波要素组合下防波堤透浪系数随挡板相对入水深度变化如图7所示,显然增大挡板相对入水深度是减少透浪的有效方法。其消能原理是增大挡板相对入水深度,一方面直接减小入射波能,另一方面两挡板间涡旋纵向尺度增大,涡旋耗能得以增大。经统计,在多数情况下,挡板相对入水深度增大10%,透浪系数可以减小10%左右。
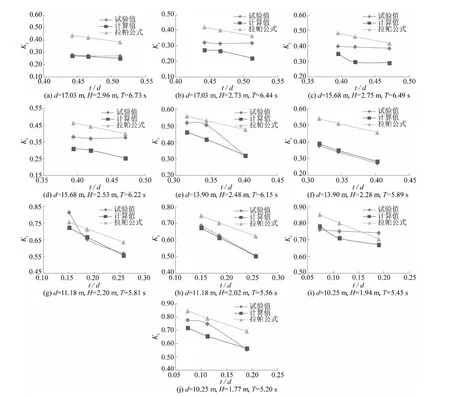
图7 挡板相对入水深度对透浪系数的影响Fig.7 The effects of relative immersed depth of barrier on transmitted coefficient
比较分析试验、数值计算和拉帕公式计算得到的透浪系数,数值计算的透浪系数结果较接近试验值,拉帕公式值普遍偏大。从三者的变化趋势上来看,数值水槽中的的计算值与拉帕公式在变化趋势上十分相似,在一些工况下的试验值变化趋势与计算值、拉帕公式也较为接近,当然也存在变化趋势不同的情况,从图7可见,这主要是由于4~5个异常数据引起的。在试验过程中发现前后挡板在波浪不断作用后有轻微晃动,形成二次造波干扰了测量的准确度,同时,试验中可能存在的操作失误也会造成数据的错误,这是某些试验值与计算值偏差较大和变化趋势异常的的重要原因。综合上面的分析,当前规范采用的拉帕公式偏差较大,而Weigel公式、Kriebel公式并不适用双侧挡板情况,建立适用于双侧挡板透空式防波堤的透浪系数公式很有必要。
3.4 堤顶相对宽度对透浪系数的影响
众所周知,影响高桩透空式防波堤透浪系数的因素不仅仅是挡板相对入水深度,还包括堤顶相对宽度B/L、相对水深d/L、相对波高H/L等。以下利用数值波浪水槽分析B/L、d/L、H/L对透浪系数Kt的影响,在此处重新设定水深 d 为10 m,波高 H 为 1.2 m、1.6 m、2.0 m、2.4 m,周期 T 为5.0 s、5.5 s、6.0 s、6.5 s,水深和波要素共16种组合,对防波堤数值模拟前对波要素进行了率定,满足数值模拟的要求;防波堤堤顶宽度B为8 m、10 m、12 m、14 m,前面已对挡板相对入水深度作详细分析,故只设置挡板入水深度t=2 m一种状况,防波堤尺寸共4 种组合,此处防波堤均设较高胸墙以排除越浪的影响 。
图8为透浪系数随堤顶相对宽度B/L的变化图。当0.159≤B/L≤0.401时,在不同工况下随着堤顶相对宽度的增大,透浪系数减小明显。随着堤顶相对宽度的增大,在水体可与堤顶接触的情况下,波浪与堤顶的接触面积增大,有利于增大摩擦耗能;另一方面,涡旋耗能随着涡旋横向尺度扩大而增强。
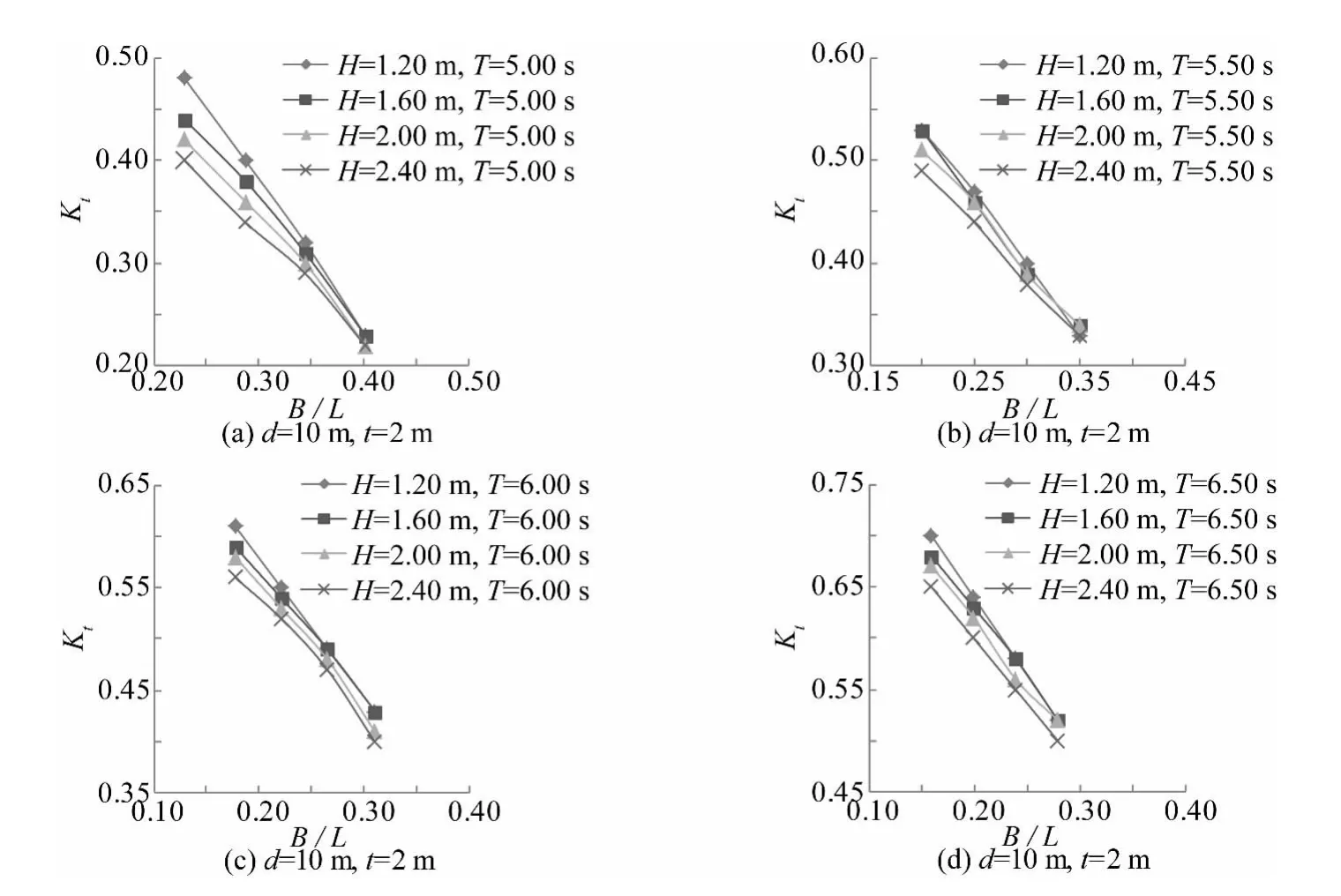
图8 堤顶相对宽度对透浪系数的影响Fig.8 The effects of relative width of horizontal plate on transmitted coefficient
3.5 相对水深对透浪系数的影响
图9所示为透浪系数随相对水深d/L的变化图。在0.199≤d/L≤0.287时,透浪系数随着相对深度的增大而减小。相对水深较大时,表层波能占总波能比例较大,堤后波高减小,这是透浪系数随着相对深度的增大而减小的根本原因。

图9 相对水深对透浪系数的影响Fig.9 The effects of relative water depth on transmitted coefficient
3.6 相对波高对透浪系数的影响
图10所示为透浪系数随相对波高的变化图。相对波高变化范围为0.024~0.069,从图10中可见,透浪系数随着相对波高的增大并未有较大变化,可见相对波高只是影响透浪系数的次要因素。
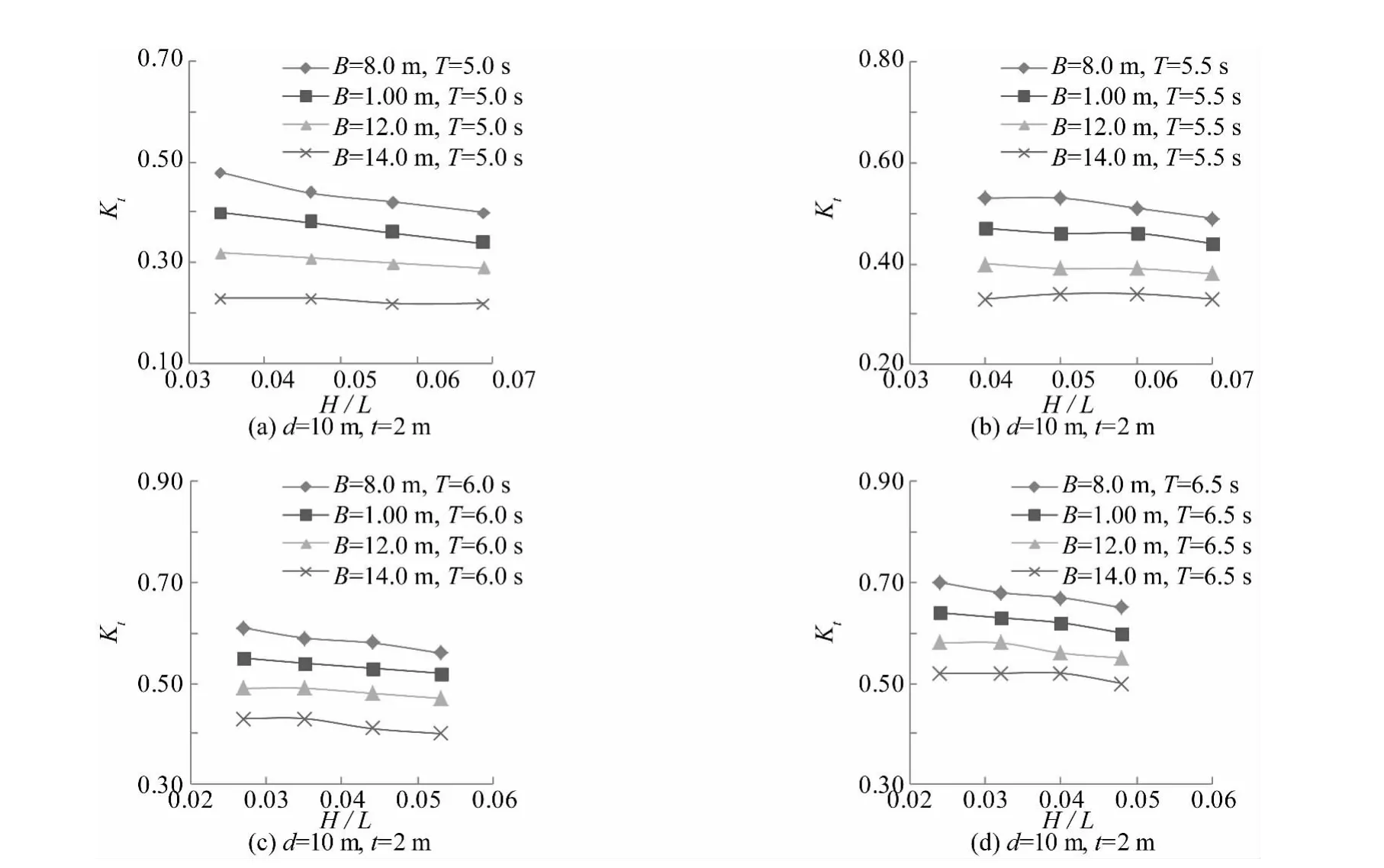
图10 相对波高对透浪系数的影响Fig.10 The effects of relative wave height on transmitted coefficient
4 透浪系数修正公式
前人公式主要考虑挡板入水深度对透浪系数的影响,忽略了堤顶相对宽度、相对水深、相对波高等因素,由上文分析可知,这些因素是难以忽略的。采用Weigel公式[2]作为修正公式的基本结构,提出考虑堤顶相对宽度、相对水深、相对波高、相对入水深度的半理论半经验公式。Weigel针对单挡板的情况,假设透射波能来自挡板下侧波能,即不考虑挡板前侧绕射波能,由此提出了透浪系数Kt的理论公式:

式中:k为波数,d为水深,t为挡板入水深度。
文中透空堤为双挡板透空式,须作如下假设:1)不考虑两块挡板的相互影响,按照Weigel公式分别计算前后两块挡板的透浪系数并相乘,以此作为修正公式的一部分;2)考虑堤顶相对宽度、相对水深、相对波高等引起的波能变化,在修正公式中加入波能修正因子α,其中:

则修正公式结构为:

因文中前后挡板入水深度相同,t1=t2=t,上式简化为:
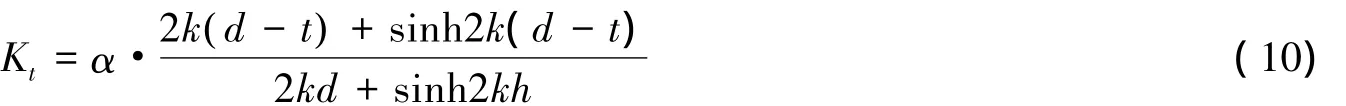
通过上文研究可知,影响透浪系数Kt的主要因素有B/L、d/L、t/d、H/L,其中B/L、d/L、t/d的影响较大,而H/L的影响相对较小。通过分析各影响因素可认为堤顶相对宽度B/L、相对水深d/L、相对波高H/L对透浪系数Kt的影响为线性关系,而考虑到图7中某些试验值的波动,将相对入水深度t/d对透浪系数的影响定为非线性作用。根据各影响因素对透浪系数的影响规律并参考冯卫兵等[20]、范骏等[21]提出的修正公式确定如下波能修正因子α公式结构:

则透浪系数修正公式结构为:
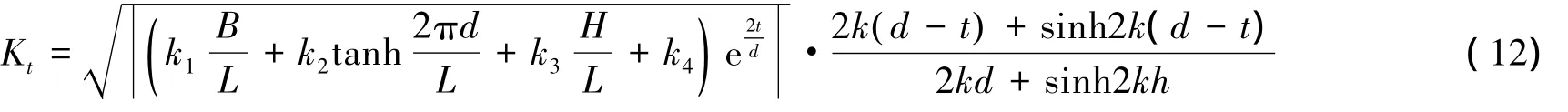
将大量数据代入公式,通过非线性拟合,可得:k1=-1.627;k2=-0.934;k3=-1.246;k4=1.720。将各系数代入上式有:

图11所示为透浪系数计算值与拉帕公式比较,可以看出,拉帕公式较计算值普遍偏大;图12所示为透浪系数计算值与修正公式值公式比较,修正公式的透浪系数值与计算值十分接近。

图11 透浪系数计算值与拉帕公式比较Fig.11 Comparison of calculated values and calculated values by Lapa formula
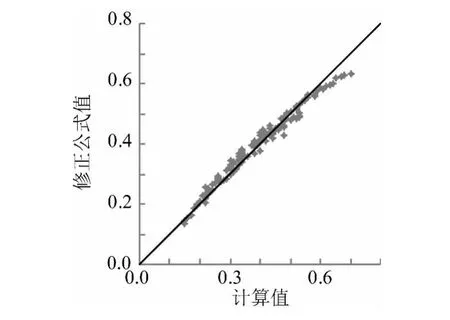
图12 透浪系数计算值与修正公式值公式比较Fig.12 Comparison of calculated values and calculated values by modified formula
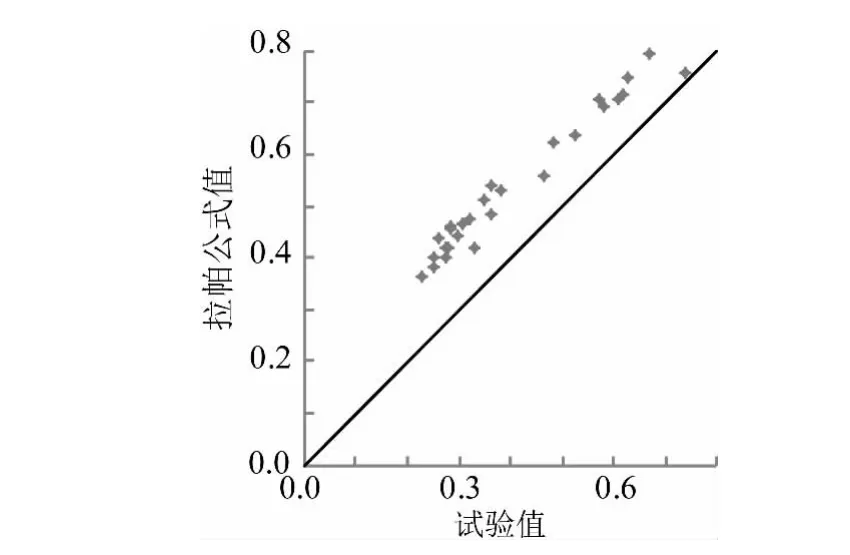
图13 透浪系数试验值与拉帕公式比较Fig.13 Comparison of experimental values and calculated values by Lapa formula

图14 透浪系数试验值与修正公式值公式比较Fig.14 Comparison of experimental values and calculated values by modified formula
图13所示为本工程物模试验透的浪系数试验值与拉帕公式比较,可以看出,拉帕公式较计算值普遍偏大,但与图11的不同之处在于拉帕公式值大于试验值的幅度是较为稳定的;图14所示为本工程物模试验透的浪系数试验值与修正公式值公式比较,约在透浪系数小于0.4时,二者吻合良好,在透浪系数较大时,二者差距略大。通过物模试验和数值计算结果分析可见,当透浪系数小于0.4时修正公式结果有较高准确度,以后可以进一步研究较大透浪系数时的修正公式。
5 结语
1)基于Fluent的源造波数值波浪水槽模拟波浪的波高、周期误差可以控制在±5%以内,完全满足波浪模型试验规程的要求。
2)利用数值波浪水槽,可以完整再现防波堤前后的水体速度矢量图和波面变化,对于深入分析挡板透空式防波堤消浪原理具有重要意义。透空式防波堤挡板相对入水深度对透浪系数影响很大,通过物理模型试验和数值计算的结果表明挡板相对入水深度增大10%,透浪系数可减小10%左右。
3)在分析堤顶相对宽度、相对水深、相对波高对透浪系数的影响后发现,堤顶相对宽度、相对水深是除挡板相对入水深度外的两个重要因素,而相对波高的影响较小。基于大量的数值计算结果,以Weigel公式为基础提出透浪系数修正公式,修正公式在透浪系数较小时与计算值吻合良好。
4)影响高桩透空式防波堤透浪系数因素众多,还包括桩、纵横梁布置等,其消浪机理和透浪系数公式还有很多不明确之处,未来可以构建三维波浪水槽,更加详细地观察和分析高桩透空式防波堤的消波原理。
[1] URSELL F.The effect of a fixed vertical barrier on surface waves in deep water[C]//Mathematical Proceedings of the Cambridge Philosophical Society.Cambridge:Cambridge University Press,1947,43(3):374-382.
[2] WIEGEL R L.Transmission of waves past a rigid vertical thin barrier[J].Journal of the Waterways and Harbors Division,1960,86(1):1-12.
[3] KRIEBEL D L,BOLLMANN C A.Wave transmission past vertical wave barriers[J].Coastal Engineering Proceedings,1996,1(25):2472-2474
[4] 邱大洪,王学庚.深水薄板式防波堤的理论分析[J].水运工程,1986,4:8-10.(QIU Dahong,WANG Xuegeng.Theoretical analysis of plate-type breakwater[J].Port& Waterway Engineering,1986,4:8-10.(in Chinese))
[5] 麻志雄.透空式防波堤消波性能试验研究[J].水运工程,1990,10(28):3-8.(MA Zhixiong.Characteristics of wave dissipation for penetrated breakwater[J].Port& Waterway Engineering,1990,10(28):3-8.(in Chinese))
[6] 严以新,郑金海,曾小川,等.多层挡板桩基透空式防波堤消浪特性试验研究[J].海洋工程,1998,16(1):67-74.(YAN Yixin,ZHENG Jinhai,ZENG Xiaochuan,et al.Characteristics of wave dissipation for pile-foundation tier-retainer breakwaters[J].The Ocean Engineering,1998,16(1):67-74.(in Chinese))
[7] 过达,蔡保华.透空式建筑物面板波浪上托力计算[J].河海大学学报:自然科学版,1980,1:14-33.(GUO Da,CAI Baohua.Calculation of open building panel uplift calculation[J].Journal of Hohai University,Natural Sciences,1980,1:14-33(in Chinese))
[8] 王国玉,王永学,李广伟.多层水平板透空式防波堤消浪性能试验研究[J].大连理工大学学报,2005:865-870.(WANG Guoyu,WANG Yongxue,LI Guangwei.Experimental study of wave-damping performance of multiple layer breakwater[J].Journal of Dalian University of Technology,2005:865-870.(in Chinese))
[9] 孙士勇.挡板(透空)式防波堤消浪效果分析[J].水运工程,1998(1):11-15.(SUN Shiyong.Analysis of wave attenuation properties of penetrated breakwater[J].Port & Waterway Engineering,1998(1):11-15.(in Chinese))
[10] MILGRAM J H.Active water-wave absorbers[J].Journal of Fluid Mechanics,1970,42(4):845-859.
[11]刘桦,王本龙,兰雅梅,等.基于FLUENT的数值波流水槽及其应用[C]//中国力学学会学术大会2005论文摘要集(下).2005:1347-1347.(LIU Hua,WANG Benlong,LAN Yamei,et al.The establish and application of wave numerical flume based on FLUENT[C]//CCTM.2005:1347-1347.(in Chinese))
[12]刘加海,杨永全,张洪雨,等.二维数值水槽波浪生成过程及波浪形态分析[J].四川大学学报:工程科学版,2005,36(6):28-31.(LIU Jiahai,YONG Yongquan,ZHANG Hongyu,et al.Making waves in 2-d numerical flume and feature analysis of the numerical waves[J].Journal of Si Chuan University,Engineering Science,2005,36(6):28-31.(in Chinese))
[13]周勤俊,王本龙,兰雅梅,等.海堤越浪的数值模拟[J].力学季刊,2006,26(4):629-633.(ZHOU Qingjun,WANG Benlong,LAN Yamei,et al.Numerical simulation of wave overtopping over seawalls[J].Chinese Quarterly of Mechanics,2006,26(4):629-633.(in Chinese))
[14]李凌,林兆伟,尤云祥,等.基于动量源方法的黏性流数值波浪水槽[J].水动力学研究与进展:A辑,2007,22(1):76-82.(LI Lin,LIN Zhaowei,YOU Yunxiang,et al.The numerical wave flume of the viscous fluid based on the momentum source method[J].Chinese Journal of Hydrodynamics,2007,22(1):76-82.(in Chinese))
[15]何军,蒋昌波,李冬,等.T型防波堤与波浪相互作用数值研究[J].海洋工程,2010,28(1):50-57.(HE Jun,JIANG Changbo,LI Dong,et al.Numerical study on T-type breakwaters interaction with wave[J].The Ocean Engineering,2010,28(1):50-57.(in Chinese))
[16]张成兴,王国玉,王永学.气幕防波堤消波性能数值模拟研究[J].水动力学研究与进展:A辑,2009,24(5):543-549.(ZHANG Chengxing,WANG Guoyu,WANG Yongxue.Numerical simulation study on wave dissipating performances of air bubbles breakwater[J].Chinese Journal of Hydrodynamics,2009,24(5):543-549.(in Chinese))
[17]兰雅梅,郭文华,宋秋红,等.基于 VOF方法的造波、消波技术[J].中国海洋平台,2010(1):22-25.(LAN Yamei,GUO Wenhua,SONG Qiuhong,et al.Wave generating and absorbin g based on VOF[J].China Offshore Platform,2010(1):22-25.(in Chinese))
[18]李凌.黏性流中水波与浮式结构物相互作用的数值模拟研究[D].上海:上海交通大学,2007.(LI Ling.The numerical simulation of interaction of water waves and floating structures in a viscous fluid[D].Shanghai:Shanghai Jiao Tong University.2007.(in Chinese))
[19]2001 JTJ,波浪模型试验规程[S].2001.(2001 JTJ,Wave model test regulation[S].2001.(in Chinese))
[20]冯卫兵,丁文林,叶小红.桩基挡板透空式防波堤透浪特性研究[J].水运工程,2014(3):62-67.(FENG Weibing,DING Wenlin,YE Xiaohong.Wave transmission coefficient of piled baffle penetrated breakwater[J].Port & Waterway Engineering,2014(3):62-67.(in Chinese))
[21]范骏,王宇楠,杨斯汉,等.双挡板透空堤透浪与反射系数实验研究[J].海洋工程,2011,29(4):60-67.(FAN Jun,WANG Yunan,YANG Sihan,et al.Experimental research on reflection coefficient and transmitted coefficient of double barriers penetrated breakwater[J].The Ocean Engineering,2011,29(4):60-67.(in Chinese))

