带扩散的Lotka–Volterra捕食模型正稳态解的存在性

尹碧妮, 曾宪忠, 顾永耕



带扩散的Lotka–Volterra捕食模型正稳态解的存在性

尹碧妮1, 曾宪忠1, 顾永耕2

(1. 湖南科技大学数学与计算科学学院, 湖南湘潭, 411201; 2. 湖南师范大学数学与计算机科学学院, 湖南长沙, 410081)

研究了一个带扩散作用的Lotka–Volterra捕食模型。使用椭圆方程的相关理论、非线性泛函分析的指数理论和度理论, 在一定条件下, 获得稳态模型正解的存在性和非存在性, 即物种共存是否存在。

Lotka–Volterra捕食模型; 正解的存在性和非存在性; Sobolev嵌入定理

生物数学模型一直是非常活跃的研究内容之一, 它能有效地刻画生物的多样性、生物拥挤、稀有生物保护问题。对于这些问题, 国内外许多数学家和生物学家已有许多研究[1–9], 并已获得了许多重要的成果。这些成果包括: 捕食问题正解(物种共存状态)是否存在性、正解的数量以及正解的稳定性; 正解曲线的分支结果; 抛物型捕食模型正解的动力行为; 以及对含有不同转换率和响应函数的模型, 对含有交叉扩散模型的研究。除了不考虑空间位置的常微分方程系统外, 一般来说, 与空间位置有关的偏微分方程系统更适合描述实际问题。

本文研究下列稳态型Lotka–Volterra捕食模型

显然, 问题(1)有一个平凡解(0, 0)和2个半平凡解(*= (, 0),*= (0,))。本文主要研究它的正解存在性。使用椭圆方程的相关理论、以及非线性泛函分析的指数理论和度理论, 在一定条件下, 获得稳态模型(1)正解的存在性(即物种共存)和非存在性。本文的结论如下:

定理 1 如果＞1且＞1(), 或者1(-) ＜≤1, 那么, 稳态问题(1)存在正解。

1 预备知识和问题(1)正解存在的必要条件

设1() ＜2()≤3() ≤…是下列问题的特征值

根据文献[8–9]可以得到以下引理2和引理3。

(i) 当≤1()时,≡ 0是问题(3)的唯一解;

(ii) 当＞1()时, 问题(3)存在唯一的正解。

让引理2中=,=。如果= 0, 那么当＞1时, 让是式(3)的唯一正解。考虑算子

引理2 让≡ 0,和如上规定, 则(i) 由式(3)产生的映射是单调增加的, 并且在(1, ∞)上可微; 当时, 并且0 ＜＜; (ii)的特征值都大于0。

进行与文献[8–9]类似的讨论, 得到下列引理。

引理3 设＞1, 如果式(1)有正解(,), 那么,＞1(), 并且0 ＜＜,＜＜+ da＜+。

2 稳态问题(1)的正解(物种共存)存在性

与文献[8–9] 类似的讨论, 得到下列2个性质。

性质1 如果0 ＜＜ 1, 0.75 ＜＜ 1且, 那么对于充分大的有。

性质2 设≠1(-)和≠1(), 则(i)(, 0) = 0; (ii) 当＞1(-)时(,*) = 0, 而当＜1(-)时(,*) = 1; (iii) 当＞1()时(,*) = 0, 而当＜1()时(,*) = 1。

定理1的证明。取一个足够大的正数＞ 1, 考虑下列问题

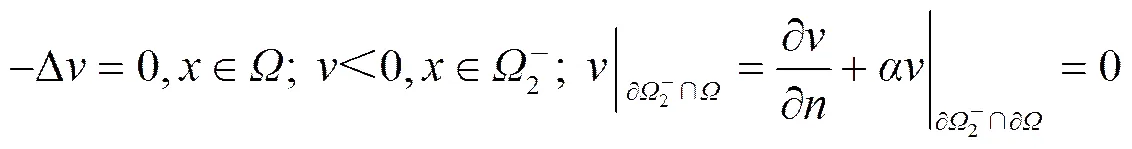
(8)

根据引理4以及≥ 0,≥ 0, 可以得到。进一步, 对于问题(8)使用椭圆方程估计理论和Sobolev嵌入定理可以得到下面的估计:。因此存在＞ 0使得, 并且对于, 辅助问题(8)在上没有解。

由以上讨论可知, 当＞1时,＞1()是问题(1)有正解(物种共存)的充要条件。

参考文献：

[1] Kuto K. Stability of steady-state solutions to a prey-predator system with cross-diffusion [J]. J Differential Equations, 2004, 197: 293–314.

[2] Du Y H, Lou Y. S-shaped global bifurcation curve and hope bifurcation of positive solutions to a predator-prey model [J]. J Differential Equations, 1998, 144: 390–440.

[3] Gu Y G, Wang M X. Existence of positive stationary solutions and threshold results for a reaction diffusion system [J]. J Differential Equations, 1996, 130: 277–291.

[4] Schreiber S J. Coexistence for species sharing a predator [J]. J Differential Equations, 2004, 196: 209–225.

[5] Lou Y, Ni W M. Diffusion vs cross-diffusion: an elliptic approach [J]. J Differential Equations, 1999, 154: 157–190.

[6] Pang P Y H, Wang M X. Strategy and stationary pattern in a three-species predator-prey model [J]. J Differential Equations, 2004, 200: 245–273.

[7] Zeng X. A ratio-dependent predator-prey model with diffusion [J]. Nonlinear Anal: Real World Applications, 2007, 8: 1 062–1 078.

[8] 曾宪忠. 带有第三边值的捕食模型的正稳态解的存在性[J]. 应用数学学报, 2006, 29(5): 801–820.

[9] 顾永耕, 曾宪忠. 被捕食者带有第三边值的捕食模型的正稳态解的存在性[J]. 数学物理学报, 2007, 27A(2): 248– 262.

[10] 叶其孝, 李正元. 反应扩散方程引论[M]. 北京: 科学出版社, 1994.

(责任编校:刘刚毅)

Existence of positive steady state solutions for a Lotka-Volterra prey-predator model with diffusion terms

Yin Bini1, Zeng Xianzhong1, Gu Yonggeng2

(1. School of Mathematics and Computing Science, Hunan University of Science and Technology, Xiangtan 411201, China; 2. School of Mathematics and Computer Science, Hunan Normal University, Changsha 410081, China)

A Lotka-Volterra prey-predator model with diffusion terms is discussed. By using some theories of the elliptic equations, the index theory and the degree theory of the nonlinear functional analysis, the existence and non-existence of its positive solutions under some conditions are obtained, i.e. whetherornothas the species coexistence.

Lotka-Volterra prey-predator model; existence and non-existence of positive solutions; degree theory

10.3969/j.issn.1672–6146.2015.02.008

O 175. 25

1672–6146(2015)02–0023–03

曾宪忠, 448397807@qq.com;尹碧妮, 710186786@qq.com。

2014–12–19

国家自然科学基金(11271120, 61402166), 湖南省自然科学基金(13JJ3085)。